[人工智能]【ML实验7】人脸识别综合项目（PCA、多分类SVM）

实验代码获取 github repo
山东大学机器学习课程资源索引

实验目的

实验环境

实验内容

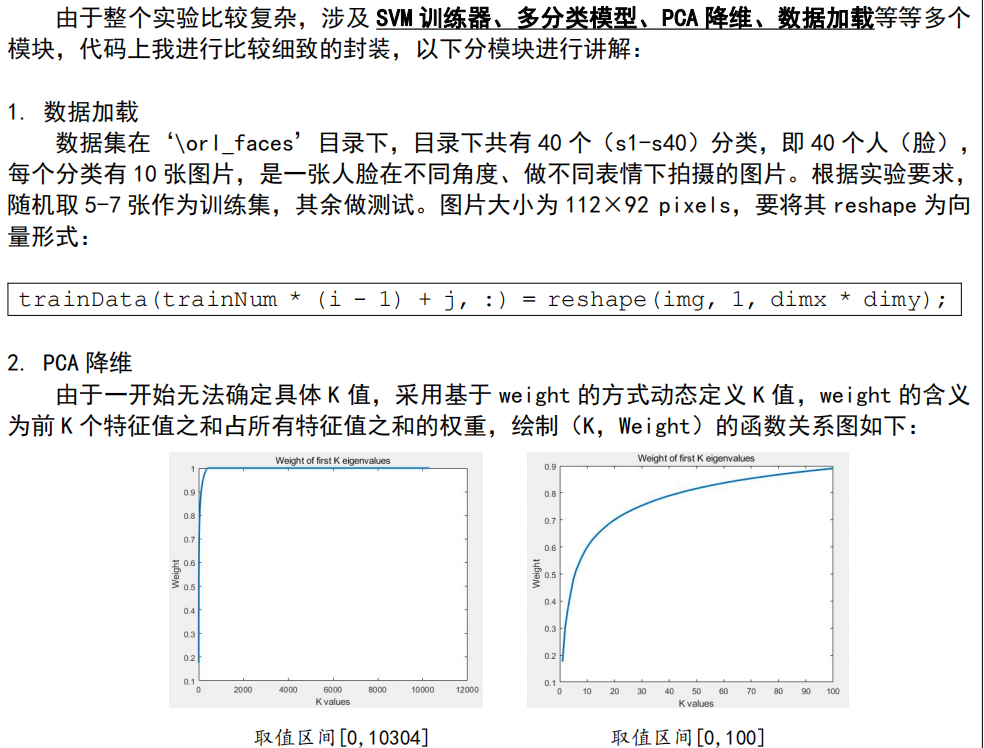
PCA

两种方法EVD-PCA和SVD-PCA的实现、效率对比见我之前的博客一个PCA加速技巧，这里补充SVD方法的数学推导：

首先，设方阵$A$的特征值分解为$A=U\Sigma U^T$，
对于矩阵$A$尝试构建一种分解
$$A=U\Sigma V^T$$
其中$U^{T}U=I,V^{T}V=I$，
效仿特征值分解，构造方阵$A^{T}A$和$A{A}^T$，
$$A^{T}A=(U\Sigma V^T{)}^{T}U\Sigma V^T=V\Sigma U^{T}U\Sigma V^T=V{\Sigma }_1^2{V}^T$$
这里我们得到了方阵$A^{T}A$的特征值分解！因此，对$A^{T}A$进行特征值分解就可以得到$V$.
同理，$A{A}^T=U{\Sigma }_2^2{U}^T$，对$A{A}^T$进行特征值分解就可以得到$U$.

下面证明对角矩阵${\Sigma }_1$和${\Sigma }_2$中的非零值相等。
设线性方程组$Ax=0$，左乘$A^T$得$A^{T}Ax=0$，因此$Ax=0$的解也是$A^{T}Ax=0$的解。
对于$A^{T}Ax=0$，左乘$x^T$得$x^T{A}^{T}Ax=0?(Ax{)}^T(Ax)=0?Ax=0$，即反过来$A^{T}Ax=0$的解也是$Ax=0$的解。
综上，$Ax=0$与$A^{T}Ax=0$有相同的解空间，可得$r(A)=r(A^{T}A)$，又有$r(A)=r(A^T)$，因此
$$r(A{A}^T)=r(A^T)=r(A)=r(A^{T}A)$$
即矩阵$A^{T}A$和$A{A}^T$同秩。
设$x$是$A^{T}A$对应特征值$\lambda$的特征向量，所以有$A^{T}Ax=\lambda x$，两边同乘$A$，得$A{A}^{T}Ax=\lambda Ax$，$A{A}^T(Ax)=\lambda (Ax)$，因此矩阵$A^{T}A$和$A{A}^T$的非零特征值相等。

而且可以得到特征值为奇异值的平方，${\lambda }_i={\sigma }_i^2$.

利用$A{A}^T$的分解构建对$A^{T}A$的分解
矩阵$A$的奇异值分解为$A=U\Sigma V^T$，两边乘$V$，得到$AV=U\Sigma$，每一列有$A{v}_i={\sigma }_i{u}_i$，即
$$u_i=\frac{A{v}_i}{\sqrt{{\lambda }_i}}$$
其中，$v_i$和${\lambda }_i$可由对$A^{T}A$的分解得到。
反之同样可行。

多分类模型

code

function [corrRate, misclass] = ovoMultiClassModel(trainData, testData, classNum, K, trainNum)
    fprintf('Running one vs one multiclass model...\n');
    %% Step 1: Assign label
    testNum = 10 - trainNum;
    N = classNum * (classNum - 1) / 2;
    trainPart = cell(N, 1); 
%     testPart = cell(N, 1);
    cnt = 1;
    map = zeros(N, 2);  % 第cnt个二分类器的对抗分类类别i,j
    
    for i = 1 : (classNum - 1)
        for j = (i + 1) : classNum
            trainPart{cnt, 1} = [[trainData((i - 1) * trainNum + 1 : i * trainNum, :), ones(trainNum, 1)]; ...
                [trainData((j - 1) * trainNum + 1 : j * trainNum, :), -ones(trainNum, 1)]];
%             testPart{cnt, 1} = [[testData((i - 1) * testNum + 1 : i * testNum, :), ones(testNum, 1)]; ...
%                 [testData((j - 1) * testNum + 1 : j * testNum, :), -ones(testNum, 1)]];
            map(cnt, 1) = i; map(cnt, 2) = j;
            cnt = cnt + 1;
        end
    end
%     save('trainPart.mat', 'trainPart');
    
    %% Step 2: Train SVM
    A = zeros(N, 2 * trainNum); % ? num(alpha)=2*trainNum
    W = zeros(N, size(trainData, 2));   % N×K
    B = zeros(N, 1);
    for i = 1 : N
        SVMObj = mySVM(trainPart{i, 1}(:, (1 : K)), trainPart{i, 1}(:, K + 1), 1);
        A(i, :) = SVMObj.alpha';
        W(i, :) = SVMObj.w';
        B(i) = SVMObj.b;
    end
    
    %% Step 3: Test classifying
    % SVM函数输出值
    totalTest = size(testData, 1);
    val = zeros(totalTest, N);
    for i = 1 : N
        val(:, i) = (testData * W(i, :)')' + B(i);
        % (?×1)=((?×K)*(1×K)')'+(?×1)，其中?为测试数据个数(totalTest)
    end
    % 第i类别参与(40×39/2)个二分类SVM中的39个
    part = zeros(classNum, classNum - 1);
    for i = 1 : classNum
        part(i, :) = find(map(:, 1) == i | map(:, 2) == i);
    end
    % f(x)=arg max_{s}∑_{t}f_{s,t}(x)
    %% A. 一对一SVM分类器结果
    res = zeros(totalTest, 1);
    for i = 1 : totalTest    % 对所有测试数据
        voteCnt = zeros(classNum, 1);
        for j = 1 : classNum    % 对所有可能分类
            for k = 1 : classNum - 1
                if val(i, part(j, k)) > 0 && map(part(j, k), 1) == j
                    voteCnt(j) = voteCnt(j) + 1;
                elseif val(i, part(j, k)) < 0 && map(part(j, k), 2) == j
                    voteCnt(j) = voteCnt(j) + 1;
                end
            end
        end
        [~, maxOne] = max(voteCnt);
        res(i) = maxOne;
    end
    %% B. 标准结果
    std = zeros(totalTest, 1);
    for i = 1 : classNum
        std((i - 1) * testNum + 1 : i * testNum) = i;
    end
    %% C. 对比统计
    corrSet = find(res == std);
    corrRate = length(corrSet) / totalTest;
    misclass = cell(1, 1);
    misclass{1} = [std, res];
    fprintf('one vs one multiclass done\n');
end

SVM训练器

code

function SVMObj = mySVM(x, y, C)
    m = size(x, 1);
    % !err：length=max(size(X))，返回数组最大维度长度
    
    options = optimset;
    options.largeScale = 'off';
    options.Display = 'off';
    
    %% A. 构建目标函数
    H = zeros(m);
    for i = 1 : m
        for j = 1 : m
            H(i, j) = y(i) * y (j) * x(i, :) * x(j, :)';
        end
    end
    f = (-1) * ones(m, 1);
    
    %% B. 构建约束
    Aeq = y';
    beq = 0;
    lb = zeros(m, 1);
    ub = zeros(m, 1);
    ub(:) = C;
    a0 = zeros(m, 1);   % 迭代初始值
    
    %% C. 利用quadprog求解器求解对偶问题
    % quadprog(H,f,A,b,Aeq,beq,lb,ub)
    [alpha, fval] = quadprog(H, f, [], [], Aeq, beq, lb, ub, a0, options);
    
    %% D. 求support vector
    alpha(find(alpha < 1e-8)) = 0;
    sv = find(alpha > 0 & alpha < C);
    w = 0;  % omega
    for i = 1 : length(sv)
        w = w + alpha(sv(i)) * y(sv(i)) * x (sv(i), :)';
    end
    num = y - x * w;
    b = sum(num(sv)) / length(sv);
    
    %% 构建返回对象SVMObj
    SVMObj.alpha = alpha;   % alpha(sv)
    SVMObj.w = w;
    SVMObj.b = b;
end

实验结果

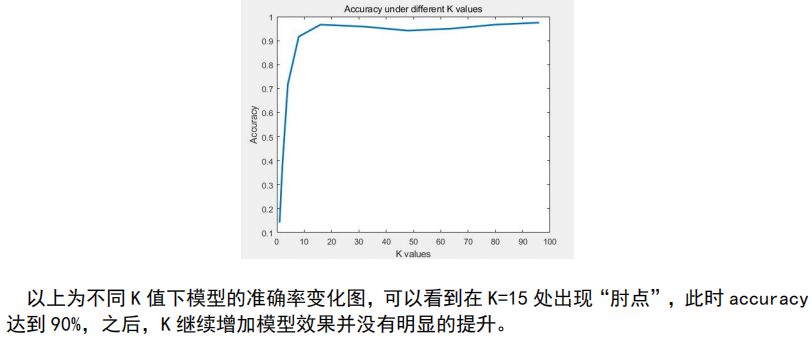
conclusion