note
- KGAT结合KG和GAT,在知识图谱三元组基础上,利用GAT进行消息传递,聚合出物品向量后与用户向量进行计算得到预测值。其实不结合KG,何向南团队之前也直接使用GNN做了NGCF和LightGCN。
- KGAT首先是CKG嵌入表示层使用TransR模型获得实体和关系的embedding;然后在attention表示传播层,使用attention求出每个邻居节点的贡献权重,需要把实体节点 h h h自身的嵌入表示 e h e_h eh?和它基于邻域的嵌入表示 e N h \boldsymbol{e}_{\mathcal{N}_h} eNh??融合起来,得到节点 h h h的新表示 e h ( 1 ) \boldsymbol{e}_h^{(1)} eh(1)?,这里的融合方法也有三种;最后的预测评估层就是用户向量和物品向量的点积结果,和真实label进行交叉熵损失函数计算loss,优化权重。
- KGAT可基于High-Order Connectivity进行表征学习。基于三个基准数据实验,KGAT效果优于CKE、RippleNet等模型。
文章目录
零、KGAT论文

论文地址:https://arxiv.org/pdf/1905.07854.pdf
论文代码:https://github.com/xiangwang1223/knowledge_graph_attention_network
一、论文动机
1.1 motivation
传统的有监督学习方法中,例如因子分解机,在抽取出样本的属性特征后,把每个样本视作一个独立的事件来预测,而忽视了样本之间内在的关系。知识图谱可以把样本之间通过属性关联起来,使得样本之间不再独立预测。KGAT基于三个基准数据实验,优于Neural FM和RippleNet等。
KGAT把用户-物品的交互二分图和知识图谱融合在一起——协同知识图CKG,即将图谱关系、用户user和item的二部交互图融合到一个图空间,以融合CF信息和KG信息,KKG也能发现更高阶的关系信息。在协同知识图 G \mathcal{G} G中:
- 节点包含实体、用户和物品;
- 关系包含原来知识图谱的关系外加一个反应用户-物品的交互关系。
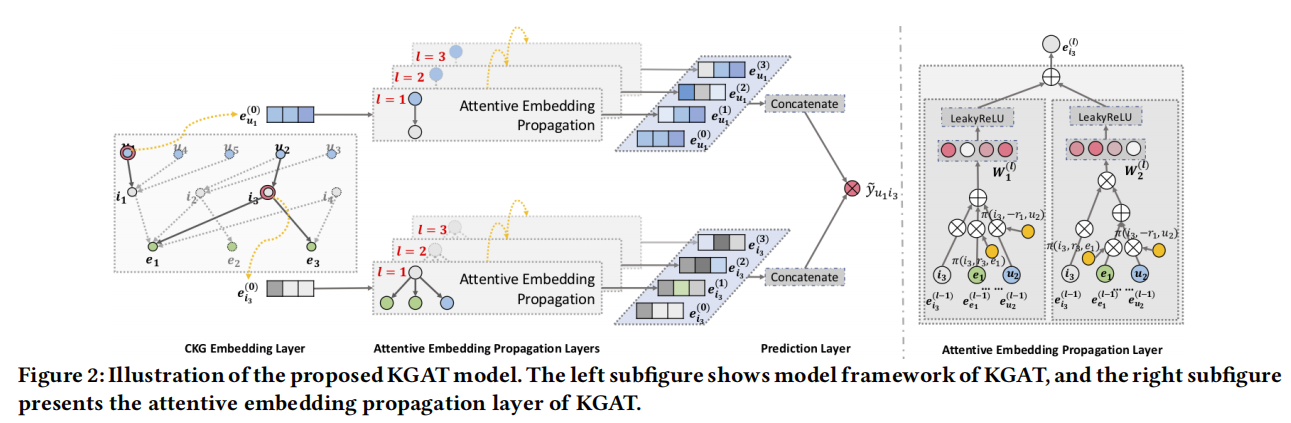
1.2 图采样和获取邻接表
获得邻居的节点embedding和关系embedding,使用get_neighbors函数,通过物品id得到其邻居及连接他们的关系的id,然后通过邻居和关系id得到邻居实体与关系的embedding的方法,而中间的adj_entity和adj_Relation分别是图采样后得到的指定度数的邻接列表。
# 得到邻居的节点embedding和关系embedding
def get_neighbors( self, items ):
e_ids = [self.adj_entity[ item ] for item in items ]
r_ids = [ self.adj_relation[ item ] for item in items ]
e_ids = torch.LongTensor( e_ids )
r_ids = torch.LongTensor( r_ids )
neighbor_entities_embs = self.entity_embs( e_ids )
neighbor_relations_embs = self.relation_embs( r_ids )
return neighbor_entities_embs, neighbor_relations_embs
adj_entity和adj_Relation即代码中的dataloader4KGNN.construct_adj函数返回值(通过kg邻接列表得到实体邻接列表和关系邻接列表),后面在消息传递时需要通过该邻接矩阵,获得当前节点的邻居节点embedding和关系embedding。
# 根据kg邻接列表,得到实体邻接列表和关系邻接列表
def construct_adj( neighbor_sample_size, kg_indexes, entity_num ):
print('生成实体邻接列表和关系邻接列表')
adj_entity = np.zeros([ entity_num, neighbor_sample_size ], dtype = np.int64 )
adj_relation = np.zeros([ entity_num, neighbor_sample_size ], dtype = np.int64 )
for entity in range( entity_num ):
neighbors = kg_indexes[ str( entity ) ]
n_neighbors = len( neighbors )
if n_neighbors >= neighbor_sample_size:
sampled_indices = np.random.choice( list( range( n_neighbors ) ),
size = neighbor_sample_size, replace = False )
else:
sampled_indices = np.random.choice( list( range( n_neighbors ) ),
size = neighbor_sample_size, replace = True )
adj_entity[ entity ] = np.array( [ neighbors[i][0] for i in sampled_indices ] )
adj_relation[ entity] = np.array( [ neighbors[i][1] for i in sampled_indices ] )
return adj_entity, adj_relation
1.3 回顾以前的GAT网络
这里的GAT我们为了简单起见使用dgl里面的dglnn.GATConv层,这里我们做的节点分类的任务。图注意神经网络(GAT)来源于论文 Graph Attention Networks。其数学定义为,
x
i
′
=
α
i
,
i
Θ
x
i
+
∑
j
∈
N
(
i
)
α
i
,
j
Θ
x
j
,
\mathbf{x}^{\prime}_i = \alpha_{i,i}\mathbf{\Theta}\mathbf{x}_{i} + \sum_{j \in \mathcal{N}(i)} \alpha_{i,j}\mathbf{\Theta}\mathbf{x}_{j},
xi′?=αi,i?Θxi?+j∈N(i)∑?αi,j?Θxj?,
GAT和所有的attention mechanism一样,GAT的计算也分为两步走:
(1)计算注意力系数(attention coefficient):(下图来自《GRAPH ATTENTION NETWORKS》)。其中注意力系数
α
i
,
j
\alpha_{i,j}
αi,j?的计算方法为,
α
i
,
j
=
exp
?
(
L
e
a
k
y
R
e
L
U
(
a
?
[
Θ
x
i
?
∥
?
Θ
x
j
]
)
)
∑
k
∈
N
(
i
)
∪
{
i
}
exp
?
(
L
e
a
k
y
R
e
L
U
(
a
?
[
Θ
x
i
?
∥
?
Θ
x
k
]
)
)
.
\alpha_{i,j} = \frac{ \exp\left(\mathrm{LeakyReLU}\left(\mathbf{a}^{\top} [\mathbf{\Theta}\mathbf{x}_i \, \Vert \, \mathbf{\Theta}\mathbf{x}_j] \right)\right)} {\sum_{k \in \mathcal{N}(i) \cup \{ i \}} \exp\left(\mathrm{LeakyReLU}\left(\mathbf{a}^{\top} [\mathbf{\Theta}\mathbf{x}_i \, \Vert \, \mathbf{\Theta}\mathbf{x}_k] \right)\right)}.
αi,j?=∑k∈N(i)∪{i}?exp(LeakyReLU(a?[Θxi?∥Θxk?]))exp(LeakyReLU(a?[Θxi?∥Θxj?]))?.
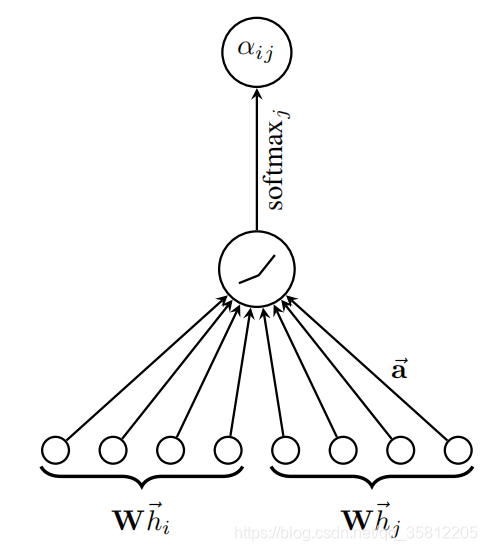
(2)加权求和(aggregate):根据(1)的系数,把特征加权求和(aggregate)

class GAT(nn.Module):
def __init__(self,in_size, hid_size, out_size, heads):
super().__init__()
self.gat_layers = nn.ModuleList()
# two-layer GAT(attention)
self.gat_layers.append(dglnn.GATConv(in_size, hid_size, heads[0], feat_drop=0.6, attn_drop=0.6, activation=F.elu))
# GATConv: in_feat, out_feat, num_head(multi-head)
self.gat_layers.append(dglnn.GATConv(hid_size*heads[0], out_size, heads[1], feat_drop=0.6, attn_drop=0.6, activation=None))
def forward(self, g, inputs):
h = inputs
for i, layer in enumerate(self.gat_layers):
h = layer(g, h)
if i == 1: # last layer
h = h.mean(1)
else: # other layer(s)
h = h.flatten(1)
return h
使用交叉熵损失函数,在dgl中我们使用train_mask表示出在训练集的节点,如果对应位置的train_mask为false则表示不会该节点不会出现在训练集。
二、KGAT模型

2.1 CKG嵌入表示层
该层为了得到知识图结构的实体和关系的嵌入表示,使用TransR模型,TransR模型使得三元组(h, r, t)在关系r的投影平面上有平移关系:
g
(
h
,
r
1
,
t
)
=
∥
W
r
e
h
+
e
r
?
W
r
e
t
∥
2
2
g\left(h, r_1, t\right)=\left\|\boldsymbol{W}_r \boldsymbol{e}_h+\boldsymbol{e}_{\mathrm{r}}-\boldsymbol{W}_r \boldsymbol{e}_t\right\|_2^2
g(h,r1?,t)=∥Wr?eh?+er??Wr?et?∥22?其中:
- W r ∈ R k × d \boldsymbol{W}_r \in \mathbb{R}^{k \times d} Wr?∈Rk×d 是关系 r r r 的变换矩阵,将实体从d维实体空间投影到k维关系空间中;
- g ( h , r , t ) g(h, r, t) g(h,r,t) 分数越小, 表示三元组 ( h , r , t ) (h, r, t) (h,r,t) 成立的概率越大,该三元组越可信。
使用pairwise ranking loss作为训练损失函数:
L
K
G
=
∑
?
h
,
r
,
t
,
t
′
?
∈
T
?
log
?
σ
(
g
(
h
,
r
,
t
′
)
?
g
(
h
,
r
,
t
)
)
\mathcal{L}_{\mathrm{KG}}=\sum_{\left\langle h, r, t, t^{\prime}\right\rangle \in \mathcal{T}}-\log \sigma\left(g\left(h, r, t^{\prime}\right)-g(h, r, t)\right)
LKG?=?h,r,t,t′?∈T∑??logσ(g(h,r,t′)?g(h,r,t))
其中:
- T = { ( h , r , t , t ′ ) ∣ ( h , r , t ) ∈ G , ( h , r , t ′ ) ? G } \mathcal{T}=\left\{\left(h, r, t, t^{\prime}\right) \mid(h, r, t) \in \mathcal{G},\left(h, r, t^{\prime}\right) \notin \mathcal{G}\right\} T={(h,r,t,t′)∣(h,r,t)∈G,(h,r,t′)∈/G} ;
- ( h , r , t ′ ) \left(h, r, t^{\prime}\right) (h,r,t′) 是负例三元组, 可以通过把正常的三元组中的尾实体替换掉得来;
- σ \sigma σ 是 Sigmoid 函数。
2.2 注意力感知的表示传播层
通过层迭代的形式吸收图上高阶的邻域信息,同时通过GAT把重要信息保存,忽略噪声信息。
先考虑一层传播的操作过程:给定一个头节点
h
h
h, 令
N
h
=
\mathcal{N}_h=
Nh?=
{
(
h
,
r
,
t
)
∣
(
h
,
r
,
t
)
∈
G
}
\{(h, r, t) \mid(h, r, t) \in \mathcal{G}\}
{(h,r,t)∣(h,r,t)∈G} ,表示以它起始的所有三元组的集合,hrt分别为头实体向量、关系向量、尾实体向量。那么节点
h
h
h 在图上的一阶邻域向量表示:
e
N
h
=
∑
(
h
,
r
,
t
)
∈
N
h
π
(
h
,
r
,
t
)
e
t
\boldsymbol{e}_{\mathcal{N}_h}=\sum_{(h, r, t) \in N_h} \pi(h, r, t) \boldsymbol{e}_t
eNh??=(h,r,t)∈Nh?∑?π(h,r,t)et?
其中:
- π ( h , r , t ) \pi(h, r, t) π(h,r,t) 反映了三元组对 h h h 的一阶邻域表示的重要程度, 也控制了有多少程度的信息从尾节点 t t t传播过来。
- π ( h , r , t ) \pi(h, r, t) π(h,r,t)的计算方法如下,其中 W r W_r Wr?关系变换矩阵,将头尾实体向量映射到 r r r向量空间后进行运算: π ^ ( h , r , t ) = ( W r e t ) ? tanh ? ( W r e h + e r ) π ( h , r , t ) = exp ? ( π ^ ( h , r , t ) ) ∑ ( h , r ′ , t ′ ) ∈ N h exp ? ( π ^ ( h , r ′ , t ′ ) ) \begin{aligned} & \hat{\pi}(h, r, t)=\left(W_{\mathrm{r}} e_t\right)^{\top} \tanh \left(W_r e_h+e_r\right) \\ & \pi(h, r, t)=\frac{\exp (\hat{\pi}(h, r, t))}{\sum_{\left(h, r^{\prime}, t^{\prime}\right) \in N_h} \exp \left(\hat{\pi}\left(h, r^{\prime}, t^{\prime}\right)\right)} \end{aligned} ?π^(h,r,t)=(Wr?et?)?tanh(Wr?eh?+er?)π(h,r,t)=∑(h,r′,t′)∈Nh??exp(π^(h,r′,t′))exp(π^(h,r,t))??
对应的一层传播代码:
# GAT消息传递
def GATMessagePass( self, h_embs, r_embs, t_embs ):
'''
:param h_embs: 头实体向量[ batch_size, e_dim ]
:param r_embs: 关系向量[ batch_size, n_neibours, r_dim ]
:param t_embs: 尾实体向量[ batch_size, n_neibours, e_dim ]
'''
# # 将h张量广播,维度扩散为 [ batch_size, n_neibours, e_dim ]
h_broadcast_embs = torch.cat( [ torch.unsqueeze( h_embs, 1 ) for _ in range( t_embs.shape[ 1 ] ) ], dim = 1 )
# [ batch_size, n_neibours, r_dim ]
tr_embs = self.Wr( t_embs )
# [ batch_size, n_neibours, r_dim ]
hr_embs = self.Wr( h_broadcast_embs )
# [ batch_size, n_neibours, r_dim ]
hr_embs= torch.tanh( hr_embs + r_embs)
# [ batch_size, n_neibours, 1 ]
atten = torch.sum( hr_embs * tr_embs,dim = -1 ,keepdim=True)
atten = torch.softmax( atten, dim = -1 )
# [ batch_size, n_neibours, e_dim ]
t_embs = t_embs * atten
# [ batch_size, e_dim ]
return torch.sum( t_embs, dim = 1 )
最后:需要把实体节点 h h h自身的嵌入表示 e h e_h eh?和它基于邻域的嵌入表示 e N h \boldsymbol{e}_{\mathcal{N}_h} eNh??融合起来,得到节点 h h h的新表示 e h ( 1 ) \boldsymbol{e}_h^{(1)} eh(1)?。融合的方式有三种选择:
- GCN聚合方法:将2个向量相加,然后经过一层非线性变换层: f C C N = LeakyReLU ? ( W ( e h + ? N h ) ) f_{\mathrm{CCN}}=\operatorname{LeakyReLU}\left(W\left(e_{\mathrm{h}}+\epsilon_{\mathcal{N}_{\mathrm{h}}}\right)\right) fCCN?=LeakyReLU(W(eh?+?Nh??))
- GraphSage聚合方法:将拼接2个向量,然后经过一层非线性变换层: f GriphtSage? = ?LeakyReLU? ( W ( e h ∥ e N h ) ) f_{\text {GriphtSage }}=\text { LeakyReLU }\left(\boldsymbol{W}\left(e_h \| e_{\mathcal{N}_h}\right)\right) fGriphtSage??=?LeakyReLU?(W(eh?∥eNh??))
- 二重交互聚合方法:考虑向量的两种交互方式——向量相加和向量的按位点积操作 ⊙ \odot ⊙,再经过一层非线性变换层: f Bi-Interiction? = LeakyReLU ? ( W 1 ( e h + e N h ) ) + LeakyReLU ? ( W 2 ( e h ⊙ e N h ) ) f_{\text {Bi-Interiction }}=\operatorname{LeakyReLU}\left(W_1\left(e_h+e_{\mathcal{N}_h}\right)\right)+\operatorname{LeakyReLU}\left(W_2\left(e_h \odot e_{N_h}\right)\right) fBi-Interiction??=LeakyReLU(W1?(eh?+eNh??))+LeakyReLU(W2?(eh?⊙eNh??))
以上是注意力感知的表示传播层操作;若要考虑更高阶的信息,可以重复堆叠多次: e h ( l ) = f ( e l t { l ? 1 ) , e N k ( l ? 1 ) ) e_h^{(l)}=f\left(e_{l_t}^{\{l-1)}, e_{N_k}^{(l-1)}\right) eh(l)?=f(elt?{l?1)?,eNk?(l?1)?)
上面的三种融合(聚合)方法对应代码:
# 消息聚合
def aggregate( self, h_embs, Nh_embs, agg_method = 'Bi-Interaction' ):
'''
:param h_embs: 原始的头实体向量 [ batch_size, e_dim ]
:param Nh_embs: 消息传递后头实体位置的向量 [ batch_size, e_dim ]
:param agg_method: 聚合方式,总共有三种,分别是'Bi-Interaction','concat','sum'
'''
if agg_method == 'Bi-Interaction':
return self.leakyRelu( self.W1( h_embs + Nh_embs ) )\
+ self.leakyRelu( self.W2( h_embs * Nh_embs ) )
elif agg_method == 'concat':
return self.leakyRelu( self.W_concat( torch.cat([ h_embs,Nh_embs ], dim = -1 ) ) )
else: #sum
return self.leakyRelu( self.W1( h_embs + Nh_embs ) )
2.3 预测评估层
该层需要把用户和物品在各层得到的向量拼接起来得到最终的表示:
e
u
?
=
e
u
(
0
)
∥
?
∥
e
u
(
L
)
,
e
i
?
=
e
i
(
0
)
∥
?
∥
e
(
L
)
e_u^*=e_u^{(0)}\|\cdots\| e_u^{(L)}, e_i^*=e_i^{(0)}\|\cdots\| e^{(L)}
eu??=eu(0)?∥?∥eu(L)?,ei??=ei(0)?∥?∥e(L)
用户对物品的偏好程度预测为两个向量的点积:
y
^
u
i
=
e
u
?
?
e
i
?
\hat{y}_{u i}=\boldsymbol{e}_u^{* \top} \boldsymbol{e}_i^*
y^?ui?=eu???ei??
推荐预测的损失函数也是成对优化误差:
L
C
F
=
∑
(
u
,
i
j
)
∈
O
?
log
?
σ
(
y
^
u
i
?
y
^
u
j
)
\mathcal{L}_{\mathrm{CF}}=\sum_{(u, i j) \in \mathcal{O}}-\log \sigma\left(\hat{y}_{u i}-\hat{y}_{u j}\right)
LCF?=(u,ij)∈O∑??logσ(y^?ui??y^?uj?)
其中:
- O = { ( u , i , j ) ∣ ( u , i ) ∈ R + , ( u , j ) ∈ R ? } O=\left\{(u, i, j) \mid(u, i) \in \mathcal{R}^{+},(u, j) \in \mathcal{R}^{-}\right\} O={(u,i,j)∣(u,i)∈R+,(u,j)∈R?}表示训练集;
- R + \mathcal{R}^{+} R+表示正样本;
- R ? \mathcal{R}^{-} R?表示负样本;
- KGAT的联合训练损失函数:
L K G A T = L K G + L C F + λ ∥ Θ ∥ 2 2 \mathcal{L}_{\mathrm{KGAT}}=\mathcal{L}_{\mathrm{KG}}+\mathcal{L}_{\mathrm{CF}}+\lambda\|\Theta\|_2^2 LKGAT?=LKG?+LCF?+λ∥Θ∥22?
其中: Θ \Theta Θ表示模型的参数集合。
三、代码
class KGAT( nn.Module ):
def __init__( self, n_users, n_entitys, n_relations, e_dim, r_dim,
adj_entity, adj_relation ,agg_method = 'Bi-Interaction'):
super( KGAT, self ).__init__( )
self.user_embs = nn.Embedding( n_users, e_dim, max_norm = 1 )
self.entity_embs = nn.Embedding( n_entitys, e_dim, max_norm = 1 )
self.relation_embs = nn.Embedding( n_relations, r_dim, max_norm = 1 )
self.adj_entity = adj_entity # 节点的邻接列表
self.adj_relation = adj_relation # 关系的邻接列表
self.agg_method = agg_method # 聚合方法
# 初始化计算注意力时的关系变换线性层
self.Wr = nn.Linear( e_dim, r_dim )
# 初始化最终聚合时所用的激活函数
self.leakyRelu = nn.LeakyReLU( negative_slope = 0.2 )
# 初始化各种聚合时所用的线性层
if agg_method == 'concat':
self.W_concat = nn.Linear( e_dim * 2, e_dim )
else:
self.W1 = nn.Linear( e_dim, e_dim )
if agg_method == 'Bi-Interaction':
self.W2 = nn.Linear( e_dim, e_dim )
# 得到邻居的节点embedding和关系embedding
def get_neighbors( self, items ):
e_ids = [self.adj_entity[ item ] for item in items ]
r_ids = [ self.adj_relation[ item ] for item in items ]
e_ids = torch.LongTensor( e_ids )
r_ids = torch.LongTensor( r_ids )
neighbor_entities_embs = self.entity_embs( e_ids )
neighbor_relations_embs = self.relation_embs( r_ids )
return neighbor_entities_embs, neighbor_relations_embs
# GAT消息传递
def GATMessagePass( self, h_embs, r_embs, t_embs ):
'''
:param h_embs: 头实体向量[ batch_size, e_dim ]
:param r_embs: 关系向量[ batch_size, n_neibours, r_dim ]
:param t_embs: 为实体向量[ batch_size, n_neibours, e_dim ]
'''
# # 将h张量广播,维度扩散为 [ batch_size, n_neibours, e_dim ]
h_broadcast_embs = torch.cat( [ torch.unsqueeze( h_embs, 1 ) for _ in range( t_embs.shape[ 1 ] ) ], dim = 1 )
# [ batch_size, n_neibours, r_dim ]
tr_embs = self.Wr( t_embs )
# [ batch_size, n_neibours, r_dim ]
hr_embs = self.Wr( h_broadcast_embs )
# [ batch_size, n_neibours, r_dim ]
hr_embs= torch.tanh( hr_embs + r_embs)
# [ batch_size, n_neibours, 1 ]
atten = torch.sum( hr_embs * tr_embs,dim = -1 ,keepdim=True)
atten = torch.softmax( atten, dim = -1 )
# [ batch_size, n_neibours, e_dim ]
t_embs = t_embs * atten
# [ batch_size, e_dim ]
return torch.sum( t_embs, dim = 1 )
# 消息聚合
def aggregate( self, h_embs, Nh_embs, agg_method = 'Bi-Interaction' ):
'''
:param h_embs: 原始的头实体向量 [ batch_size, e_dim ]
:param Nh_embs: 消息传递后头实体位置的向量 [ batch_size, e_dim ]
:param agg_method: 聚合方式,总共有三种,分别是'Bi-Interaction','concat','sum'
'''
if agg_method == 'Bi-Interaction':
return self.leakyRelu( self.W1( h_embs + Nh_embs ) )\
+ self.leakyRelu( self.W2( h_embs * Nh_embs ) )
elif agg_method == 'concat':
return self.leakyRelu( self.W_concat( torch.cat([ h_embs,Nh_embs ], dim = -1 ) ) )
else: #sum
return self.leakyRelu( self.W1( h_embs + Nh_embs ) )
def forward( self, u, i ):
# # [ batch_size, n_neibours, e_dim ] and # [ batch_size, n_neibours, r_dim ]
# 得到邻居的节点embedding和关系embedding
t_embs, r_embs = self.get_neighbors( i )
# # [ batch_size, e_dim ]
h_embs = self.entity_embs( i )
# # [ batch_size, e_dim ]
Nh_embs = self.GATMessagePass( h_embs, r_embs, t_embs )
# # [ batch_size, e_dim ]
item_embs = self.aggregate( h_embs, Nh_embs, self.agg_method )
# # [ batch_size, e_dim ]
user_embs = self.user_embs( u )
# # [ batch_size ]
logits = torch.sigmoid( torch.sum( user_embs * item_embs, dim = 1 ) )
return logits
注意:上面其实是做了一个简化(在CKG嵌入层使用nn.embedding),没有使用联合训练,如果要看联合训练的完整代码,请参考 https://github.com/LunaBlack/KGAT-pytorch。
四、实验结果
在三个基准数据集:Amazon-book、Last-FM和Yelp2018数据集上实验,KGAT与SL (FM和NFM)、基于正则化(CFKG和CKE)、基于路径(MCRec和RippleNet)和基于图形神经网络(GC-MC)的方法进行了比较:

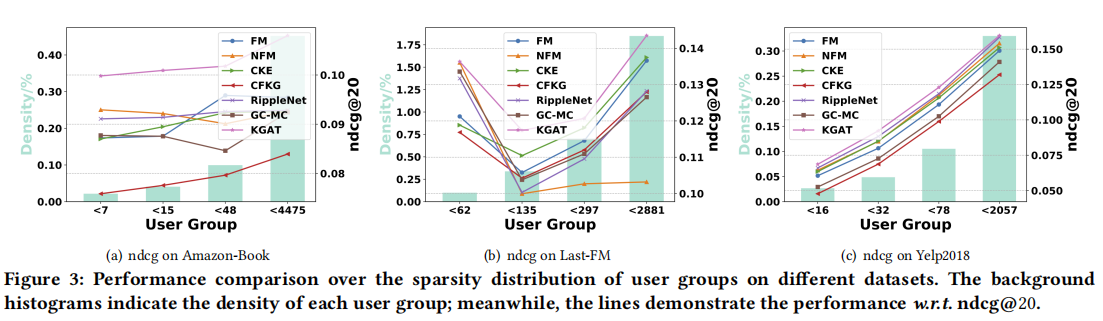
为了探索聚合器的影响,作者考虑了使用不同设置的KGAT-1变体,即之前提到的GCN、GraphSage和Bi-Interaction,实验结果如下表所示。可以看出,Bi-Interaction的性能最好:

Reference
[1] 推荐系统前沿与实践. 李东胜等
[2] 自然语言处理cs224n-2021–Lecture15: 知识图谱
[3] 东南大学《知识图谱》研究生课程课件
[4] 2022年中国知识图谱行业研究报告
[5] 浙江大学慕课:知识图谱导论.陈华钧老师
[6] https://conceptnet.io/
[7] KG paper:https://github.com/km1994/nlp_paper_study_kg
[8] 北大gStore - a graph based RDF triple store
[9] Natural Language Processing Demystified
[10] https://github.com/datawhalechina/team-learning-nlp/tree/master/KnowledgeGraph_Basic
[11] 新一代知识图谱关键技术综述. 东南大学 王萌
[12] cs224w(图机器学习)2021冬季课程学习笔记12 Knowledge Graph Embeddings
[13] 关系抽取和事件抽取代码案例:https://github.com/taishan1994/taishan1994 (西西嘛呦)
[14] 年末巨制:知识图谱嵌入方法研究总结
[15] “知识图谱+”系列:知识图谱+图神经网络
[16] 【知识图谱】斯坦福 CS520公开课(双语字幕)
[17] https://github.com/LIANGKE23/Awesome-Knowledge-Graph-Reasoning
[18] 再谈图谱表示:图网络表示GE与知识图谱表示KGE的原理对比与实操效果分析
[19] WSDM’23 | 工业界搜推广nlp论文整理
[20] https://github.com/LunaBlack/KGAT-pytorch
[21] 推荐系统之深度召回模型综述(PART III)
[22] 深度融合 | 当推荐系统遇上知识图谱(二)
[23] KGAT_基于知识图谱+图注意力网络的推荐系统(KG+GAT)
[24] KGAT的pytorch完整代码
[25] 美团基于知识图谱的个性化新闻推荐系统