Stochastic Back Propagation (Reparametrization Trick)
本章主要介绍的是,神经网络用
正常情况下简单举例
假设
那么很自然的可以将此函数看成,{
假设,
条件概率密度函数}
假设目标分布为
实际上可以将
网络的模型如下所示:
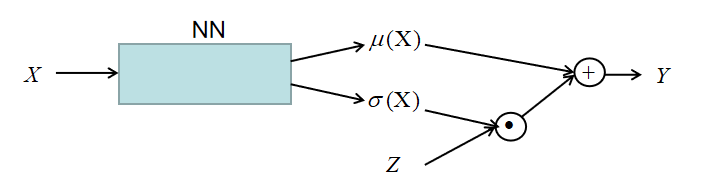
其中,
链式求导法则为:
这样就可以做到用NN来近似概率密度函数,观测这个式子发现
小结
这小结从用神经网络来近似概率分布的角度分析两种概率分布模型,简单的高斯分布和条件高斯模型。并简要的介绍了其链式求导法则。
总结
本章节主要是对于概率生成模型进行了一个全面的介绍,起到一个承上启下的作用。回顾了之前写到的浅层概率生成模型,并引出了接下来要介绍的深度概率生成模型。并从任务(监督 vs 非监督),模型表示,模型推断,模型学习四个方面对概率生成模型做了分类。并从极大似然的角度重新对模型做了分类。并介绍了概率图模型和神经网络的区别,我觉得其中最重要的是,概率图模式是对样本数据建模,其图模型有具体的意义;而神经网络只是函数逼近器,只能被称为计算图。
参考B站视频【机器学习】【白板推导系列】
更多干货,第一时间更新在以下微信公众号:

您的一点点支持,是我后续更多的创造和贡献

转载到请包括本文地址 更详细的转载事宜请参考文章如何转载/引用
本文由 mdnice 多平台发布