1、一元线性回归
R方在一元线性回归模型中,衡量【响应变量X和预测变量Y】的线性关系。
R方=cor(X,Y)^2
但是,在多元线性回归模型中,因为涉及多个预测变量,全部R方就是衡量响应变量和多个预测变量当中的关系。
而有关系数,只是衡量一对变量当中的关系,全部就不可以推广了。
2、多元线性回归模型
R平方=cov(y,yi)^2
这当中有关系数的两个变量变成,响应值和线性回归的预测值了。当然一元线性也同样适用了。
对于R方
一般回归模型
R方是统计学里常用的统计量,在不同任务模型下的解读和用途不一,有时候会出现误用情况。本文总结了对R方的理解和用法,遵循“从一般到特殊”的思路,先讲一般回归模型中的R方,再讲线性回归模型里的R方。"一般"回归模型包括线性模型,随机森林,神经网络等。
- R方的定义
R方的名字是coefficient of determination,另一个名字是Nash–Sutcliffe model efficiency coefficient。给定一系列真值 yi 和对应的预测值y^i,R方的定义为
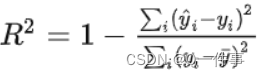
R方的含义是,预测值解释了 yi 变量的方差的多大比例,衡量的是预测值对于真值的拟合好坏程度。通俗理解,假定 yi 的方差为1个单位,则R方表示"使用该模型之后, yi 的残差的方差减少了多少"。比如R方等于0.8,则使用该模型之后残差的方差为原始 yi 值方差的20%。
- R方=1:最理想情况,所有的预测值等于真值。
- R方=0:一种可能情况是"简单预测所有y值等于y平均值",即所有 y^i 都等于yˉ(即真实y值的平均数),但也有其他可能。
- R方<0:模型预测能力差,比"简单预测所有y值等于y平均值"的效果还差。这表示可能用了错误模型,或者模型假设不合理。
- R方的最小值没有下限,因为预测可以任意程度的差。因此,R方的范围是 (?∞,1] 。
- 注意:R方并不是某个数的平方,因此可以是负值。
参考文献:https://zhuanlan.zhihu.com/p/143132259
皮尔逊相关系数中的方差
对于不固定截距的简单线性模型(y = mx + b), R方等于x和y的pearson correlation coefficient的平方。因此,此处的R方范围是[0,1]。R方等于0,表示x和y的散点图完全随机,没有线性关系(或者说,线性相关关系等于0)。R方等于1,表示所有(x,y)散点落在一条直线上。
参考文献:https://zhuanlan.zhihu.com/p/143132259
学习用,如有侵权,请联系删除。