深入浅出CenterFusion

Summary

自动驾驶汽车的感知系统一般由多种传感器组成，如lidar、carmera、radar等等。除了特斯拉基于纯视觉方案来进行感知之外，大多数研究还是利用多种传感器融合来建立系统，其中lidar和camera的融合研究比较多。

CenterFusion这篇文章基于nuscenes数据集研究camera和radar的特征层融合，图像部分采用的是CenterNet，radar点云部分采用了pillar expansion后通过roi frustum来与图像检测到的box进行匹配，radar特征提取与CenterNet类似，利用radar点云的vx、vy以及depth分别构建heatmap后与图像特征进行拼接来完成融合。官方代码仓库链接

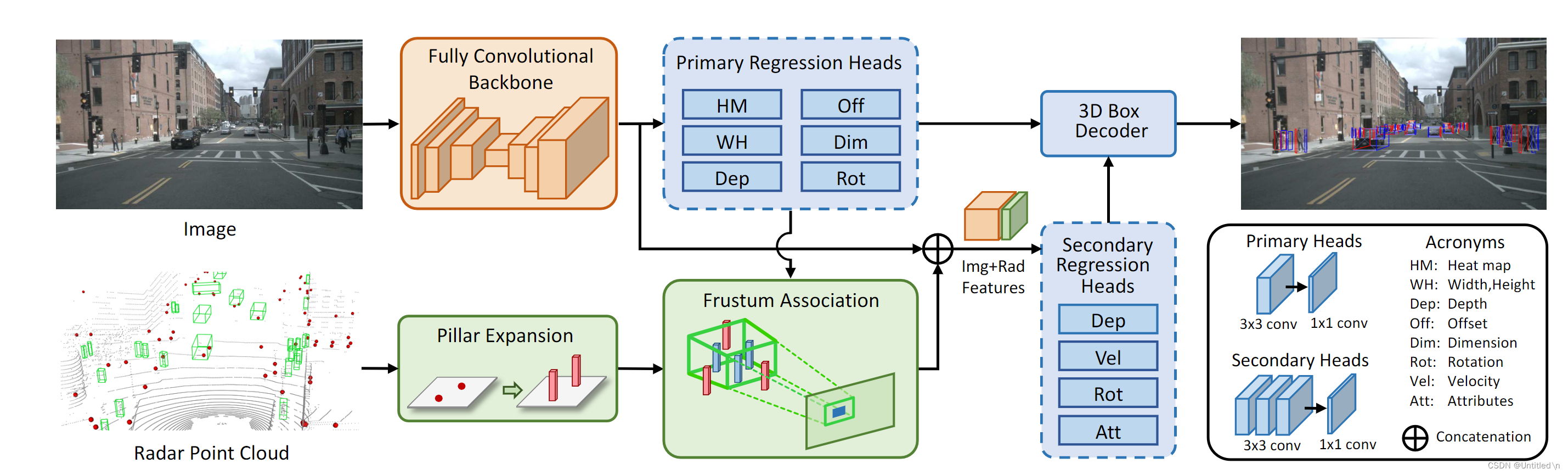
总体思路还是将雷达点云投射到图像数据中，特征层进行通道拼接，再利用卷积网络进行回归。检测分为两个阶段，Primary Regression Heads的结果除了输出外，还用来进行点云数据和box的匹配；Secondary Regression Heads由于拼接了雷达特征，可以修正Primary Regression Heads的预测结果，同时给出额外的信息，目标速度和属性等等。

主要解决了如下问题：

问题	方案
毫米波雷达点云数据有很多杂波，和真实物体经常是一对多的关系，难以与图像box进行匹配	利用3D视椎体来过滤和筛选点云，加快匹配速度，同时过滤无效的点云
一般的毫米波雷达点云数据没有高度信息，很难准确与图像中的box进行匹配	Pillar Expansion, 将点扩充为3D pillar，增大匹配概率
毫米波雷达点云数据非常稀疏，以致于表征能力弱，在整个网络中的权重较低	利用与之匹配的box来扩充雷达点云覆盖范围，由一个点转变成一小块矩形区域，提取点云headmap作为点云特征

图片特征提取及Primary Regression
修改了CenterNet的Head，利用全卷积backbone进行特征提取的时候，进行一个初步的回归，得到目标的2D Box 和3D Box
雷达点云和2D图像目标匹配
- 3D 视椎体
  利用Primary Regression Heads得到的每个3D Box的深度depth、观测角alpha、3D框尺寸dim，再加上相机标定矩阵来生成3D视椎体（每个可能的Box都生成一个），类似Roi提取，加快匹配速度的同时，过滤无效的点云。
  
  观测角和标定矩阵是为了计算yaw角
- 雷达点云Pillar Expansion
  雷达点云没有高度信息，将点云扩充为固定大小的3D柱子，增大点云匹配的概率（相对用点表示目标物，用柱子表示能够增加在3D空间中的体积，进而增大匹配的概率）
- 点云匹配
  pillar投影到pixel坐标系与2D box进行匹配; pillar投影到相机坐标系与构造的3D视椎体进行深度值匹配
雷达点云特征提取
对于每一个与视椎体关联到雷达目标，利用图像中2D检测框的位置生成三张headmap，三张heatmap concat到图片的特征中作为额外通道，进而完成融合
利用融合特征进行Secondary Regression
除了估计目标速度之外，还重新估计了目标的深度和角度（结合了雷达特征，估计更精确）
3D Box Decoder
综合Primary和Secondary Regression Heads的输出，还原出3D目标检测结果（位置、大小、姿态、速度，以及类别等属性），其中dep和rot在两个heads里都有，则只利用准确度更高的second regression heads

背景知识

如果没有了解过相关内容，可以按下顺序来看，CenterFusion里的大部分代码都是来自于CornerNet和CenterNet

重点内容

网络结构

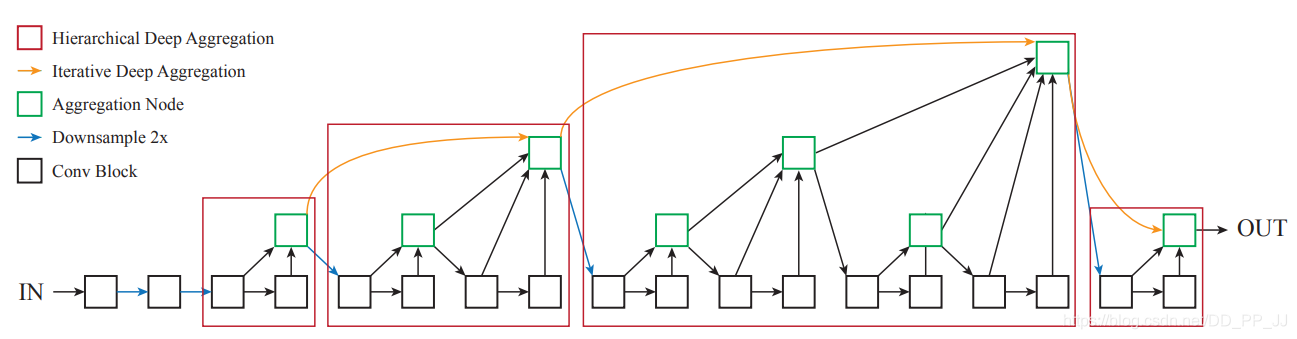
Backbone沿用了CenterNet的DLA-34, 并将可变形卷积DeformConv引入。关于网络结构内容可参考CenterFusion(基于CenterNet)源码深度解读: ：DLA34

雷达点云和2D图像目标匹配

基于视锥的匹配

3D视椎体缩小了匹配范围，进而加快匹配速度
相比于直接将雷达点云投射到2D图像，3D视锥能够区分2D图像中重叠或被遮挡的目标
使用参数 $\delta$ 来调节 ROI 视椎体的大小，这是为了解决估计的深度值的不准确性，因为ROI视椎匹配时，使用的深度值 $\hat{d}$ 是通过图像特征估计出来的。调节视椎体大小的目的是为了尽可能的给每一个box找到至少一个雷达点云来匹配，即使匹配到多个点云，后面直接取深度最小的点云来完成box内的点云去重。如下为BEV视角示意图

只在infer阶段用参数δ，实际调节的是视椎体的深度范围, 增加此参数的目的更多是降低漏检率。

代码中用frustumExpansionRatio来表示调节参数，根据视锥体的深度范围计算得到一个dist_thresh,
其中 $\delta = dist\_thresh * frustumExpansionRation$ ， $\hat{d}$ 是primary head输出的3D box depth或GT depth。图中绿色虚线是经过调节的视锥体深度值范围，深度值在此范围内的雷达点云，与这个对应的box匹配。其中roi frustum和dist_thresh构造程序如下：
```
# 对每一个3D box，计算roi frustum的8个角点, roi frustum为3D box的包围盒，
# 且roi frustum在pixel坐标系下的投影为2D box
def comput_corners_3d(dim, rotation_y):
    # dim: 3
    # location: 3
    # rotation_y: 1
    # return: 8 x 3
    c, s = torch.cos(rotation_y), torch.sin(rotation_y)
    # dim是全局坐标系下的长宽高，下面计算的也是全局坐标系下的3D box的8个角点
    # 自动驾驶车辆在地面上行驶，一般只考虑偏航角，利用rotation_y构造旋转矩阵
    R = torch.tensor([[c, 0, s], [0, 1, 0], [-s, 0, c]], dtype=torch.float32)
    l, w, h = dim[2], dim[1], dim[0]
    x_corners = [l/2, l/2, -l/2, -l/2, l/2, l/2, -l/2, -l/2]
    y_corners = [0, 0, 0, 0, -h, -h, -h, -h]
    z_corners = [w/2, -w/2, -w/2, w/2, w/2, -w/2, -w/2, w/2]

    corners = torch.tensor(
        [x_corners, y_corners, z_corners], dtype=torch.float32)
    
    # 全局坐标下的3D box的8个角点左乘旋转矩阵，得到roi frustum的8个角点,
    # 对应的roi frustum在pixel坐标系下的投影，刚好为2D box
    corners_3d = torch.mm(R, corners).transpose(1, 0)
    return corners_3d


def get_dist_thresh(calib, ct, dim, alpha):
    rotation_y = alpha2rot_y(alpha, ct[0], calib[0, 2], calib[0, 0])
    corners_3d = comput_corners_3d(dim, rotation_y)
    dist_thresh = max(corners_3d[:, 2]) - min(corners_3d[:, 2]) / 2.0
    return dist_thresh
```

雷达点云目标和图像2D目标一般是多对一的关系，如果视锥体内有多个雷达点云，则只保留深度最小（距离最近）的点云，消除冗余的雷达点云数据。匹配结果如下:

top image: 将雷达点云扩充为3D Pillar后投影到pixel坐标系
middle image: 根据点云的深度直接将3D Pillar 投射到2D图像。点云去重前
bottom image: 视锥匹配后，同时对雷达点云进行特征提取，将点云heatmap并投射到2D图像。点云去重后

视锥的使用并不是先例, TLNet和Frustum PointNet等anchor based方法均利用了视锥来过滤anchor，因为稠密的anchor带来巨大的计算量，2D检测结果形成的3D视锥可以过滤掉大量背景上的anchor。


TLNet	Frustum PointNet

雷达点云特征提取

因为图像是经过CenterNet转换成了heatmap，同时对雷达点云和图像中的BOX进行了一对一的匹配，为了将图像数据和雷达点云数据更好的融合，论文将雷达点云特征转换为heatmap，进而在通道上拼接(concat)来完成融合。

具体为，将点云数据的深度、速度x分量，速度y分量作为三个通道。对每一个与雷达点云匹配的2D Box，在2D Box内部分别以三个通道值填充一个Box（暂称为次级Box），次级Box的中心与原始2D Box的中心重合，大小与原始Box成比例, 比例通过 $\alpha$ 参数控制

注: 雷达测量的速度是径向速度

$F_{x, y, i}^{j}=\frac{1}{M_{i}}\left\{\begin{array}{ll} f_{i} & \left|x-c_{x}^{j}\right| \leq \alpha w^{j} \quad \text { and } \\ & \left|y-c_{y}^{i}\right| \leq \alpha h^{j} \\ 0 & \text { otherwise } \end{array},\right.$

三个通道分别为 $\left(d, v_{x}\right. \left.v_{y}\right)$ ，其中i是雷达的特征图通道，且 $i\in 1,2,3$ ， $M_{i}$ 是每个通道的归一化因子， $c_{x}^{j}, c_{y}^{j}$ 是与之匹配的第 $j$ 个2D box的中心坐标， $w^{j}, h^{j}$ 是第 $j$ 个2D box的宽和高， $\alpha$ 是一个超参数，用于控制次级Box的大小。

点云heatmap的分布与CenterNet有些差异，CenterNet的heatmap是以中心点的取值生成的高斯分布，而点云heatmap是以2D box中心点生成一个成比例大小的Box，Box内取值相同，Box外取值为0。

其他

目标角度in-bin regression

做过机器学习的都知道，有一个重要的步骤叫做特征工程，某个变量难以直接拟合或拟合效果不好时，需要进行一些encoding。因为直接回归角度标量有点困难，可以先大致判断位于哪个角度区间，然后在区间内进行offset回归

论文中不直接回归观测角 $\alpha$ ，而是将 $\alpha$ 取值范围编码为两个bins: $[\frac{-7pi}{6}, \frac{pi}{6}], [\frac{-pi}{6}, \frac{7pi}{6}]$ 。每个bin包含4个标量，维度合计为8。对于一个bin,两个值用作softmax分类，其余两个值对每个bin中的角度中值的offset进行回归。这里其实是沿用了CenterNet的角度回归方式。代码如下:

def _add_rot(self, ret, ann, k, gt_det):
    if 'alpha' in ann:
        ret['rot_mask'][k] = 1
        alpha = ann['alpha']
        if alpha < np.pi / 6. or alpha > 5 * np.pi / 6.:
            ret['rotbin'][k, 0] = 1
            ret['rotres'][k, 0] = alpha - (-0.5 * np.pi)
        if alpha > -np.pi / 6. or alpha < -5 * np.pi / 6.:
            ret['rotbin'][k, 1] = 1
            ret['rotres'][k, 1] = alpha - (0.5 * np.pi)
        gt_det['rot'].append(self._alpha_to_8(ann['alpha']))
    else:
        gt_det['rot'].append(self._alpha_to_8(0))

def _alpha_to_8(self, alpha):
    ret = [0, 0, 0, 1, 0, 0, 0, 1]
    if alpha < np.pi / 6. or alpha > 5 * np.pi / 6.:
        r = alpha - (-0.5 * np.pi)
        ret[1] = 1
        ret[2], ret[3] = np.sin(r), np.cos(r)
    if alpha > -np.pi / 6. or alpha < -5 * np.pi / 6.:
        r = alpha - (0.5 * np.pi)
        ret[5] = 1
        ret[6], ret[7] = np.sin(r), np.cos(r)
    return ret

CentNet论文的附录给出了详细公式,，Loss分为两部分：前半部分用softmax分类，判断角度位于哪个bin，损失函数为cross entropy ；后半部回归角度关于对应bin中心取值（就是角度平均值）的offset，对offset取正弦或余弦值作为角度残差，并计算与角度残差GT的L1 loss

$L_{\text {ori }}=\frac{1}{N} \sum_{k=1}^{N} \sum_{i=1}^{2}\left(\operatorname{softmax}\left(\hat{b}_{i}, c_{i}\right)+c_{i}\left|\hat{a}_{i}-a_{i}\right|\right)$
其中 $c_{i}=\mathbb{1}\left(\theta \in B_{i}\right), a_{i}=\left(\sin \left(\theta-m_{i}\right), \cos \left(\theta-m_{i}\right)\right)$ ， $ \hat{b}_{i}$是groud truth, 表示该角度属于第几个bin, $m_{i}$ 为第i个bin的中心取值。

观测角可以通过下面的公式得到， $j$ 是classfication score较大的那个bin的index。即通过角度所属bin的中值，加上一个三角函数offset，得到观测角度。
$\hat{\theta}=\arctan 2\left(\hat{a}_{j 1}, \hat{a}_{j 2}\right)+m_{j}$

代码中将角度八元组表示为rot, 后处理时会转换成观测角alpha和航向角yaw（又称rotaition_y）

def get_alpha(rot):
    # rot: (B, 8) [bin1_cls[0], bin1_cls[1], bin1_sin, bin1_cos,
    #                 bin2_cls[0], bin2_cls[1], bin2_sin, bin2_cos]
    # return alpha[B, 0]
    idx = rot[:, 1] > rot[:, 5]
    alpha1 = torch.atan2(rot[:, 2], rot[:, 3]) + (-0.5 * 3.14159)
    alpha2 = torch.atan2(rot[:, 6], rot[:, 7]) + (0.5 * 3.14159)
    # return alpha1 * idx + alpha2 * (~idx)
    alpha = alpha1 * idx.float() + alpha2 * (~idx).float()
    return alpha

def alpha2rot_y(alpha, x, cx, fx):
    """
    Get rotation_y by alpha + theta - 180
    alpha : Observation angle of object, ranging [-pi..pi]
    x : Object center x to the camera center (x-W/2), in pixels
    rotation_y : Rotation ry around Y-axis in camera coordinates [-pi..pi]
    """
    rot_y = alpha + np.arctan2(x - cx, fx)
    if rot_y > np.pi:
        rot_y -= 2 * np.pi
    if rot_y < -np.pi:
        rot_y += 2 * np.pi
    return rot_y

为什么这样进行角度估计

网络拟合的是观测角alpha的相关编码，最后还是要通过相机内参转换为航向角，那么为什么不直接拟合航向角呢？

因为航向角是相对于世界坐标系的，而观测角是相对于相机坐标系的。所以网络拟合的是观测角，但是最终输出的是航向角。除了这个原因之外，Bounding box estimation using deep learning and geometry. In CVPR, 2017
的4.1章指出：仅通过目标的图像估计其全局偏航角是不可能的，并提出了MultiBin Orientation Estimation，CenNet系列论文均参考了此类方法。

由下图可以看出，目标的偏航角保持固定的情况下，随着位移的改变，其局部图像上看似乎发生了旋转，导致相对角度发生了变化。"看上去"就像汽车在旋转一样。这种特性对于CNN而言极其不利，因为如果采用全局偏航角作为ground truth，CNN需要将看上去转角不同的图像映射到同一个答案上，即多对一情况，这完全无法训练出准确的结果。

因此论文采用局部相对角（目标朝向相对相机射线）来作为GT，即通过估计图中的 $\theta_{l}$ ，再通过几何关系间接得到全局偏航角，图中为 $\theta$ 。针对 $\theta_{l}$ ，采用了MultiBin Orientation Estimation方法，将角度划分为几个区间，预测落在哪个区间，以及相对区间的offset。CenterNet系列文章拟合是观测角 $\alpha$ 的编码, $\alpha$ 与这里的 $\theta_{l}$ 存在几何关系