[区块链]论文阅读学习：GHOST：Secure High-Rate Transaction Processing in Bitcoin

若有错误之处还请批评指正。后面会继续完善的~

简介

比特币的TPS不能满足高额的交易处理，用户的增加使得系统将需要扩展以更高的速率处理交易，而以前的安全保证可能就会出现差错。较大的块大小或更频繁的块创建事件（这是增加交易吞吐量所必需的）会导致块之间的更多冲突，在攻击中安全级别会急剧降低。
为了缓解这种情况，比特币社区的成员建议了一些块压缩方法，例如，仅传输交易哈希（大小几乎减少了 16 倍），或者应用Invertible Bloom Lookup Table (IBLT)(也叫Invertible Bloom Filter (IBF)(可逆布隆过滤器),用来表示部分同步模式下一个生产者的状态和完全同步模式下一个节点的状态 )来传达交易节点子集之间的差异[3]。另一种方法是使用无信任的链外交易渠道，通过更新只有在合理的资金转移后才承诺给区块链的交易，该交易渠道会慢慢地将少量的资金转移给另一方。这种方法有一些缺点：资金必须锁定，在通道存在期间无法使用，它只允许聚合维护通道的双方之间的事务，最后，它对于构建在块链之上的其他协议（如以太坊）并不总兼容，在这些协议中，单个更新不能以类似的方式聚合。

作者提出了另一种替代最长链规则的ghost，它改变区块链的冲突解决过程。ghost在链中的每个分叉选择位于分叉上最重的子树，此项工作也设计了交易确认时间。
值得注意的是，除了降低双重攻击攻击的难度外，其他几个问题随之出现：首先，与网络连接更好的矿工获得的回报略大于他们分享的哈希功率，其次，Eyal和Sirer探索的自私采矿策略可以被较弱的矿工使用。这两个问题仍然没有被ghost协议单独解决。在一篇论文中（inclusive blockchain protocol），我们探索了另外的方向（与ghost兼容），它降低了高度连接矿工的优势，并提供了额外的吞吐量增加。

模型

有向图 $G=(V,E)$ ，每个节点 v在整个网络中拥有计算能力$p_v\ge 0$，对于每个v来说$p_v=1$.网络中的每个节点v 都根据泊松过程生成块， 速率为$p_v?\lambda$，使整个网络组合在 泊松过程中以速率生成块 = （协议的当前值$\lambda =\frac{1}{600}$，比特币成立时选择的）。我们假设每条边$e\in E$都有与它相关的延迟 $d_e$，这仅仅是发送一个区块传播所需的时间。

在受到攻击的网络中，我们将使用$\lambda ={\lambda }_h$ 作为诚实网络中块的创建率。对于某些q > 0 ,攻击者的速率相对于诚实网络的对比为$q?{\lambda }_h>0$。与诚实的网络相比，我们假设攻击者正在有效地创建长链：它的块总是建立在彼此之上 .

对于每个块B，我们按time（B）表示其绝对的创建时间。这些块基本上形成了一个一时间为导向的以创世区块为根的树结构;我们表示这棵树时间t的结构为tree（t），subtree（B）表示以B为根的子树。最后，depth（B）表示树中 B 块的深度。

树的结构受兄弟节点的影响。从形式上讲，我们把这个选择建模为一个函数s（·)，该函数将区块链树 $T=（V_T，E_T）$映射到下一个块的父区块$B\in V_T$。每个节点都可能对树的全局拥有不同的观点（它可能没有接收到所有被创建的块），因此它只知道它目前已知的树。
Bitcoin 协议目前要求节点在已知的最长链条的末端构建新块。因此，我们用longest（t）表示树tree（t）上最深的叶子。除非明确说明，否则我们假设节点遵循此规则。

术语"主链"将相对应从起源块到叶子选择扩展的路径（通常为longest(t))，节点认为主链是事务历史记录的唯一可接受版本。其增长率是衡量系统性能的核心指标之一。从形式上讲，主链从长度 $n=1$ 到$n$所需的时间是一个随机变量，我们将其表示为${\tau }_n$。 $\tau ={\lim }_{n\to \infty }\frac{1}{n}{\sum }_{i=1}^n{\tau }_n$，$\beta =\frac{1}{E[\tau ]}$,$\beta$ 是主链的块添加速率，λ是块添加到区块树上的速率（一个是主链，一个是全部的网络，速率不一样）。
协议中另一个参数是最大的块大小（KB），由b表示。我们假设整个论文对交易处理的需求很高，并且块始终达到极限。
最后，我们定义比特币可扩展性的主要指标为系统添加到主链的每秒交易数（TPS）。我们按$K$表示每KB的平均交易次数。那么现在TPS就可以表示成$TPS(\lambda ,b):=\beta (\lambda ,b)?b?K$.

高吞吐量下安全性降低

假设攻击者以$q?{\lambda }_h$的速度创建块.如果 $q?{\lambda }_h$大于网络主链的增长率$\beta$，无论它打算绕过和替换链的当前长度（根据大量定律）,攻击总是成功的（给予足够的时间）。相反，如果$q<\frac{\beta }{{\lambda }_h}$攻击者链绕过主链的概率随着主链长度的增加呈指数级下降（请参阅 定理 10 以获得证明）。因此，我们认为该比率$\frac{\beta }{{\lambda }_h}$是系统的"安全阈值"。
协议的吞吐量受两个基本参数的影响：块创建率$\lambda$和块大小$b$。为了加快区块的创建过程，可以降低创建有效块所需的计算问题的难度。同样，如果想要增加块大小，则可以允许较大的块传播。一种比较天真的想法就是说只需增加这两个参数，就可以尝试增加吞吐量。我们认为，这两种修改都增加了树中分叉数量，这反过来又导致系统安全阈值的降低。换句话说，一旦吞吐量增加，攻击者就可以用更少的计算能力进行有效的攻击。这些参数之间的定性权衡如图所示。

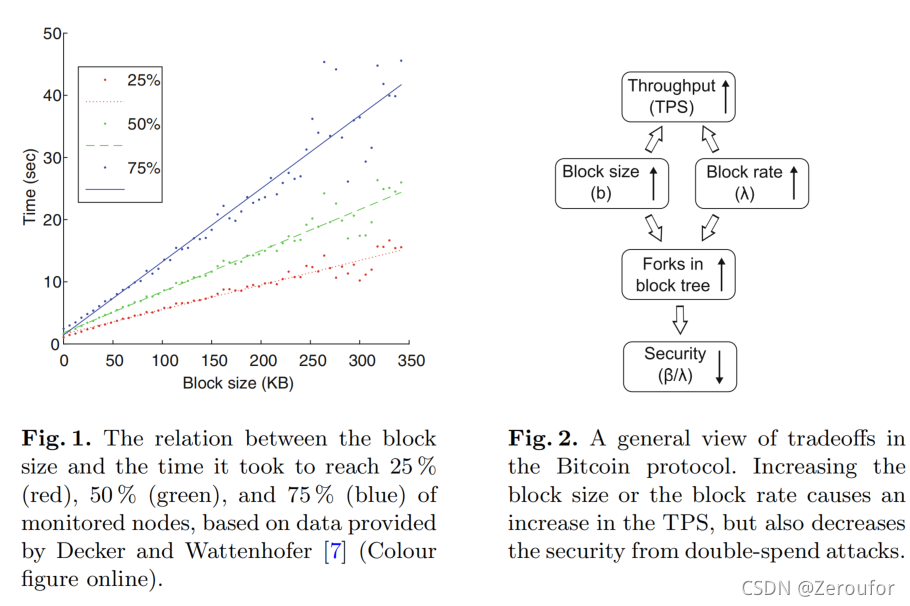
增加区块大小。事实上，虽然节点尚未得知主链的最新新增部分，但它创建的任何块不会添加到该链中，而是有助于更新较少的替代分支（这里我也不知道为啥，我觉得是只对自己增加的那个链一直挖矿，因为现在自己看到的那里是最长的，但实际上不是）。因此，随着块大小的增加，块自然需要更长的时间通过网络传播，因此会发生更多的分叉。图1测量了比特币中的块传播延迟，描绘了块大小和它的传播时间之间的明确线性关系。（这种情况下先挖到区块的人会有较大的优势挖下一个块，拥有更多算力的矿工或者矿池就会更有优势，会导致挖矿的集中化，导致硬分叉，失去向后的兼容性）
提高区块生成速率。同样，如果区块生成速率增加，则诚实的网络（更大的${\lambda }_h$）会创建更多的块，主链中的最新块被传播。 同样，这些块通常由未完全更新且不会延长最长链条的节点创建。另一方面，攻击者也会更快地创建区块（以$q?{\lambda }_h$ 的速度），但不遭受效率损失.更快的区块创建速率通常意味着交易以更快的额速度得到确认。（这种方式会增加孤块出现的概率，从而造成计算资源的浪费，有效哈希计算的比率降低，降低网络安全性，节点之间需要更多的通信，增加带宽的需求。）
安全性降低。 在上述两种情况下，创建的区块并不总是有助于主链的延长，这使得攻击者更容易替换它。
图3 说明了一个场景，诚实的网络创建了一个高度分叉的区块链树。攻击者秘密创建 6 个区块（表示为 1A，2A,…， 6A）， 这显然比网络最长的链条长（以块 5b 结尾） 。如果块传播的更快（相对于创建速率），则诚实网络树上的所有区块都会形成一条长长的链条，并且不会被攻击者超越。

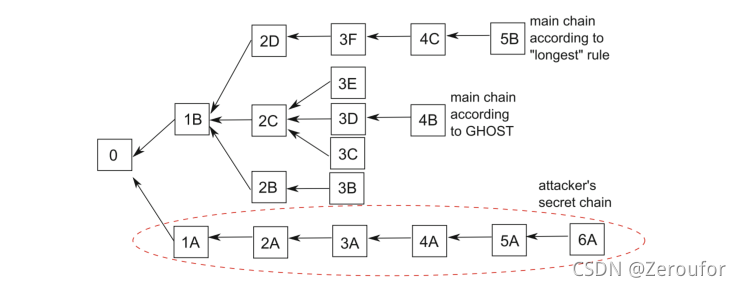
The Greedy Heaviest-Observed Sub-Tree (GHOST)

该协议的好处是它能够保证安全阈值一直在50%，而不是$\frac{\beta }{{\lambda }_h}$。它允许系统以大尺寸的区块和较快的出块速率运行。
任何节点都根据一个策略$s(T)$选择下一个区块的父结点，该策略将树T映射到T中代表主链的一个块。ghost是一个新的选主策略。这个新策略重新定义了主链。
对于树T中的块B，$subtree（B）$是以B为根的子树，$Childre{n}_T（B）$是直接引用B 作为其父的区块集合。由$GHOST（T）$表示我们提议的选主策略，定义为以下算法的输出：

对于一个给定的树T，首先创世区块加入其中，如果直接引用他的集合为空，那么返回这个区块并退出（叶子节点，最新的）；如果不为空，则更新为现在的最大权重子树，一直循环选择主链。这里每个分叉都去选择最重子树。

GHOST的基本性质

当运行ghost时，每个节点的账本应该是一样的。${\psi }_B$定义的每个块B被所有节点放弃或被所有节点采用的最早时刻。我们将所有节点采用的区块称为分叉的崩溃。
提案2（账本统一）：$pr（{\psi }_B<\infty ）=1$。换句话说，每个区块最终要么完全被抛弃，要么被完全采用。此外，$E[{\psi }_B]<\infty$。
证明：D为网络的延迟直径。假设当$t>time（B)$时块B既不是被所有节点采用，也不是被所有节点抛弃。${?}_t$表示系统中的下一个块创建发生在时间 $t+D$ 和$t+2D$之间，然后在时间$t+3D$之前不产生其他块的事件。我们认为，一旦发生此类事件，所有节点要么采用或放弃块B。事实上，在时间 t 和t+D之间，所有节点都能看到所有已经存在的块（因为没有制造新的），因此，每个拥有相同祖先的同等重量的子树的叶子节点都有节点积极尝试去扩展它们。然后创建一个打破这些联系的块，另一个时间单位D内允许它传播到所有节点，使得每个节点的账本保持一致。请注意，$Pr（{?}_t）$（在t时间内）的下界是一个正数，因为它不依赖于 t（因为指数分布是无记忆的）。因此，第一个${?}_t$事件的期望等待时间是有限的。停止时间$B_{\psi }$是上限，根据定义和第一个${?}_t$的等待时间，意味着$E[{\psi }_B]<\infty$。

自己的理解：在t到t+D时间内，节点可以看到在时间t前已经被附加到树上所有的区块，但是时间t内创建的区块还没有被看到，至少在时间D以后新的区块被所有节点看到，也就是如果在时间t+D和t+2D之间，剩下的一个D时间内没有新的区块产生，那么就可以决定一个分支是完全被采纳还是全部都被抛弃。在t到t+D时间内，如果有子树的重量相等，那么当有一个分支率先打破僵局，并且时间D内传播给了所有节点，那么所有节点仍然会选择这个分支使得账本保持一致，就不会在自己认为是主链的非主链分支上进行计算了。

在概率理论和统计学中，指数分布（也称为负指数分布）是描述泊松过程中的事件之间的时间的概率分布，即事件以恒定平均速率连续且独立地发生的过程。
指数函数的一个重要特征是无记忆性（Memoryless Property，又称遗失记忆性）。这表示如果一个随机变量呈指数分布，当s,t>0时有$P(T>t+s|T>t)=P(T>s)$
期望值$E=\frac{1}{\lambda }$

GHOST 链选择规则的主要优势是它具有 50% 的攻击能力，即使在高速率或网络出现重大延迟的情况下：通过等待足够长的时间(在块创建之后)，其状态从"接受"更改为"放弃"的可能性可以任意变小。

提案3（对50%攻击的留置权）:假设攻击者的块创建速率是$q?{\lambda }_h$和 $0\le q<1$ 。块 B 可能会在会在$time(B)+\tau$后离开主链，它$time(B)+\tau$时在主链中，当$\tau$趋于无穷时趋于零。
对比之前说保证抵御50%的攻击的安全阈值为$q<\frac{\beta }{{\lambda }_h}$。此命题表明，在遵循 GHOST 规则的任何网络中，安全阈值为 1。
证明：B 最终从主链中被丢弃的事件包含在尚未发生崩溃的情况下（即${\psi }_B\ge time(B)+\tau$）。再次依赖于$E[{\psi }_b]$的有限性(提案2)，以及运用马尔可夫不等式， 它表明，当$time(B)+\tau$时，B已经放弃或已经被所有（诚实）节点采用的概率为1。在前一种情况下，这个命题成立很简单.在后一种情况下，区块以${\lambda }_h$的速度在创造B的子树，这比$q?{\lambda }_h$高。因此，随着$\tau$增长，subtree（B）与攻击者链之间的差距越来越大，使得攻击在未来某个时候任意成功的可能性任意低（大量定律）。

我的理解：就是一个极限情况。在$time(B)+\tau$这个时间节点，之前B还在主链上，因为攻击者攻击成功后之后就不在了。那么在$time(B)+\tau$及之前，所有诚实节点都还在主链上进行计算，而且所有的生成速率为${\lambda }_h$，那么在q在0-1的条件下，攻击者的生成块的速率$q?{\lambda }_h$肯定比诚实者要低。随着时间增长，肯定B还在主链上的概率大。

GHOST的崩溃率。之前已经讨论了任何区块B 的崩溃时间${\psi }_B$及其对 GHOST 主链的生长和融合的影响。长时间存在的分叉意味着更长的等待时间，直到整个网络确认到一个块，并进一步意味着交易授权的等待时间更长。进一步调查 B 的崩溃发生速度可能很有用。我们这样做的简单模型，只有两个分叉，每个分叉具有相等的计算能力。即使是这个看似简单的案例也被证明是非平凡的。

定理4:考虑一个有两个节点的网络，u和 v，它们都以$\frac{\lambda }{2}$ 的速度创建块，这些块通过带有延迟 d的单个链接连接。对于任何块B ， $E(n_B)\le \frac{{d\lambda }^2}{8}+\frac{d\lambda }{2}$,其中,对于$T=tree({\psi }_B)$来说$n_B:=|subtre{e}_T(B)|$
定理为两个节点提供了上界：这是最糟糕的情况，一般来说，设置崩溃发生得更快。

ghost和最长链的主链增长

会两种方式下主链（$\beta$）的增长率进行分析。由于这个增长率高度依赖于网络的确切拓扑，这既未知又极其难以衡量，我们采取双重方法：首先，我们从上界和下界对增长率进行分析。其次，我们模拟具有随机抽样覆盖拓扑的网络，并测量得到区块树。然后，我们将继续讨论这些结果在每个规则的安全性、吞吐量和资源使用方面的影响。

下界

引理 5 （最长链和延迟边界） 。$G=（V，E）$是网络图（整个网络的子图），在直径为D的网络的图以速率${\lambda }^{{}^{\prime }}=\alpha ?\lambda$生成块,。在最长链规则下，最长链的生长速度为$\beta (\lambda )\ge \frac{{\lambda }^{{}^{\prime }}}{1+{\lambda }^{{}^{\prime }}?D}$ 。
下面是引理5的证明：

我理解的证明是，首先每个块的生成时间是随机的，$X_i$是两个块创建之间的时间，是随机变量（它表示的间隔是传播时延D加上网络创建下一个块的指数分布）。因为创建一个块的划那他的生长率，也就是主链的增加速率至少为1，生长率=生长速率*生长时间，这里生长速率就是β，生长时间是一个符合指数分布的随机变量X。在n足够多的情况下，我们可以将$X_i$看作均匀随机的变量.
指数分布是描述泊松过程中的事件之间的时间的概率分布，即事件以恒定平均速率连续且独立地发生的过程，符合模拟标准。
$\beta (\lambda )\ge \frac{1}{E(X)}$,生长率至少为1，在大数定律中，E(X)表示为$E(\frac{1}{n}{\sum }_{i=1}^n{X}_i)$,上面有说这个随机变量它表示的间隔是传播时延D加上网络创建下一个块的指数分布，即D+E（Y），指数分布中期望为$\frac{1}{\lambda }$,把它带入E(Y)中，然后得证。

引理 6 （Ghost和延迟边界） 。$G=（V，E）$是网络图（整个网络的子图），在直径为D的网络的图以速率${\lambda }^{{}^{\prime }}=\alpha ?\lambda$生成块,。在GHOST规则下，最长链的生长速度为$\beta (\lambda )\ge \frac{{\lambda }^{{}^{\prime }}}{1+2{\lambda }^{{}^{\prime }}?D}$ 。

引理5和6都可以证明是紧致的。边界可在具有n额节点的完全图下达到。$n\to \infty$，其中所有边的延迟都恰好为D，每个节点具有1/n’的计算能力。因此，这个下界可以被认为是近似于理想的分散网络，其中计算能力很好地分布在许多等距的节点之间。
引理5 直观地遵循以下事实：在深度为n的节点U被创建并发送到所有节点（D秒）后，需要$\frac{1}{\lambda }$ 秒的期望时间才能创建下一个块$U^{{}^{\prime }}$。 由于$U^{{}^{\prime }}$ 的创造者肯定知道U的创建，因此其深度必须至少为 n + 1。因此，这个下界稍微比率为：$\frac{1}{D+\frac{1}{{\lambda }^{{}^{\prime }}}}=\frac{{\lambda }^{{}^{\prime }}}{1+{\lambda }^{{}^{\prime }}?D}$ 。
由于GHOST没有选择最长链，可以预期其主链的增长率将略低于最长的链条规则。确实如此。然而，增长率的损失相对较小，与最长链规则不同，它与GHOST的安全无关。

[会慢慢更新，发现证明有点多了，哈哈]