一、门罗币（monero）介绍

门罗币(Monero)是一个衍生自比特币的开源加密货币，门罗币的设计基于CryptoNote 协议，并且提供了更强的隐私保护特性。在身份隐私保护方面,首先门罗币沿用了比特币中基于椭圆曲线公钥密码体制的匿名身份认证技术，门罗币中每个用户随机生成两个椭圆曲线公钥(A,B)作为用户的公开身份标识，相对应的私钥(a,b)由每个用户私自持有，并在交易过程中用于生成签名信息，完成用户的身份认证和支付确认。但它不同于比特币所使用的NIST 曲线和ECDSA 签名算法，门罗币选用了设计更为公开和高效的ED 25519 数字签名模式；其次，门罗币实现了交易过程中的身份隐藏机制，它使用环签名实现了交易发送方的身份隐藏,使用隐蔽地址(stealth address)实现了交易接收方的身份隐藏。

二、隐蔽地址(stealth address)原理

1.原理分析

门罗币沿用了比特币中的UTXO 交易模型并设计了基于隐蔽地址的交易接收方身份隐藏机制。在每次交
易过程中，通过使用发送方生成的随机数和接收方的身份标识(A,B)来运行一个半Diffie-Hellman 密钥交换协议
派生出一个一次性接收地址，从而将真正的交易接收方身份隐藏在整个可能的用户空间中，而只有持有相应私
钥(a,b)的人才能够判断出这是一笔发送给(A,B)的交易。此时对于系统总用户数为N 的情况，观察者可成功判断
出接收方身份的概率为1/N。

2.示例

设椭圆曲线中的基点为G,G 的阶数为 $l$ ,则门罗币中的隐蔽地址计算流程如图所示:
在这里插入图片描述

(1) Alice 想要付款给Bob，Alice 先需获取Bob 的公钥信息 $(A, B)$ ;
(2) Alice 产生一个随机数 $r\in [1,l-1]$ ，然后计算一次性公钥 $P=H_{s} (rA)G+B$ ;
(3) Alice 计算 $R = r G$ ，然后生成一笔交易将 $P$ 作为目的地址,并将 $R$ 也放入交易中;
(4) Alice 将交易广播到区块链上;
(5) Bob 检查区块链上每一笔交易，并用他自己的私钥 $(a, b)$ 计算出相应的 $P{}' =H_{s} (rA)G+B$ ，因为 $a R = a r G = r A$ ，如果 $P=P{}'$ ,那么说明这笔交易就是发送给自己的;
(6) Bob 找到自己的交易后就可以算出对应的一次性私钥 $x'=H_{s}(aR)+b$ ,且 $P^{'} = x^{'} G$ ,他可以使用私钥 $x^{'}$ 签名交易来进行支付.

3.子地址问题

为了满足门罗币用户使用和管理多个地址(身份标识)的需求,类似于比特币中的HD 钱包方案，门罗币又提
出了用户子地址(sub-address)的概念，用户可通过自己的主钱包地址派生出任意数量的不可链接的子地址。在进行交易接收地址搜索时，使用主私钥进行一次计算既可以判断出是否为子地址对应的输出地址，从而避免了使用多个私钥进行多次计算匹配的复杂操作开销。用户通过自己的主钱包地址 $(A, B)$ 和索引 $i$ 派生出相应的子地址并存储在列表中,生成方法如图所示：

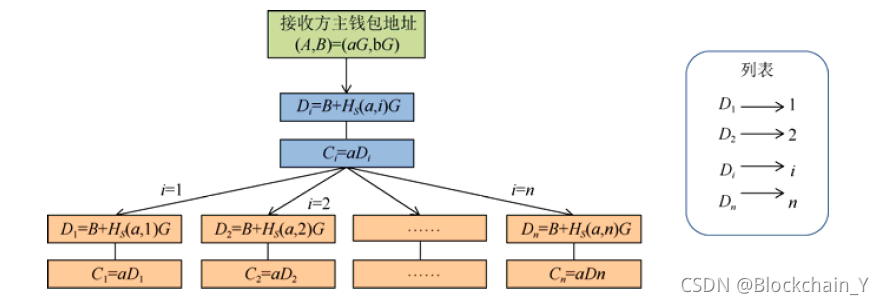
在这里插入图片描述
交易过程中生成的一次性子地址的判断方法如下图所示。接收方在判断子地址时只需通过主私钥 $a$ 、一
次性子地址 $P$ 和交换的随机变量 $R$ 进行计算获得 $D'_{i}$ 并和列表中的 $D_{i}$ 比较即可。匹配成功后，用户可通过主私钥 $(a, b)$ 和索引 $i$ 生成相应的一次性私钥。
在这里插入图片描述

三、环签名

门罗币中交易发送方的身份隐藏是通过环签名技术来实现的。环签名是由Rivest 等人在如何匿名泄漏秘
密背景下提出来的新型签名技术。环签名不同于群签名，它在构造匿名集合的过程中无需配置过程和管理者。在环签名中，签名者将自己的公钥和另外一些公钥(但不知道私钥)进行混淆构成匿名集合，然后再对消息进行签名。这样对于观察者而言，无法区分签名来自匿名集合中的哪一个公钥(真正的签名者)。环签名的定义如下：
给定一个环 $U={U_1,U_2,U_3,…,U_n}$ ，环中每个成员的公私钥对为 $pk_i,sk_i),i=1,2,...,n$ 。不失一般性，假设 $U_k(1≤k≤n)$ 是签名人，则环签名、验签算法可如下定义：

1.环签名生成算法

由签名人运行。其输入是待签名的消息 $m$ 、环中所有成员的公钥 $pk_i$ 、真正签名人的私钥 $sk_k$ ；其输出就是 $U_k$ 对消息m 的环签名 $\sigma$ 。

2.环签名验证算法

由签名验证者运行。其输入是待验证的消息签名对 $(m,\sigma)$ 、环中所有成员的公钥，当接受该签名时输出为1，否则输出为0。

门罗币中所使用的是一类具有可链接性的环签名，称为可链接环签名。可链接性是指如果环 $U={U_1,U_2, U_3,…,U_n}$ 中的某个签名人产生了两个消息签名对 $(m,\sigma _{1} )$ 、 $(m,\sigma _{2})$ ，则存在有效算法使得签名验证者可以确定这两个消息是由环中同一个签名人产生的。其中，判断链接性的算法如下定义：

签名链接算法 ：其输入是环 $U={U_1,U_2,U_3,…,U_n}$ 的两个消息签名对 $(m,\sigma _{1} )$ 、 $(m,\sigma _{2})$ ，当签名 $\sigma _{1}$ 、 $\sigma _{2}$ ，是由同一个环成员产生时,算法输出为1，否则为0。

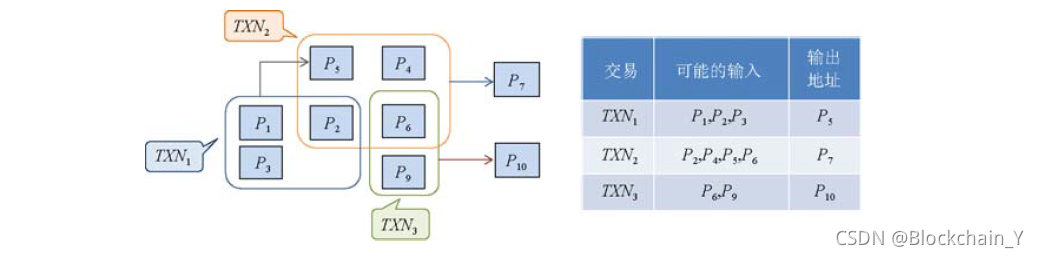
门罗币用户在进行交易时首先执行自主混币过程，即搜索链上具有相同面额的 $U T X O$ ，选择它们的公钥和自身公钥一起来构成环(匿名集合)；其次，用户通过自身私钥和环成员的公钥对支付消息生成环签名；最后，验证节点验证环签名的有效性和链接性(防双花)。门罗币自主混币过程的实例如图所示：以其中的交易 $TXN_2$ 为例,交易发送方 $P_4$ 与具有同等货币面额的支付者 $P_2、P_5、P_6$ 混淆在一起构成一个环进行交易。对于观察者来说，通过支付信息和签名无法辨别出交易发送方的真实身份。

通过对上述分析可知，门罗币采用基于可链接环签名技术的混淆方案实现了如下3 个功能：(1) 利用环签名的匿名性将交易发送方的身份隐藏在环成员构成的匿名集合中；(2) 利用环签名的不可伪造性实现了用户对交易行为的确认和不可否认；(3) 利用可链接环签名的可链接性防止货币(UTXO)双花(double spending)。

在这里插入图片描述