第一章:期权市场机制
文章目录
前言
期权作为重要的金融衍生产品,在风险对冲,套期保值,价格发现,套利等方面发挥着重要的作用,特别是我国金融衍生品的发展速度较快,如何更好的理解期权产品内涵,知道期权交易的基础知识,掌握关于期权的常见数理模型,是一个金融专业学生的基础素养,也是对期权感兴趣的交易者需要清楚的.这个系列的博文是我个人将自己所掌握的关于期权的内容进行系统整理,对于文中大部分内容,我都会使用python软件进行复现和量化,希望大家能够一起学习,共同进步.
一、期权类型
要了解期权,首先需要认识什么是衍生产品,因为期权是衍生产品的一种.通俗而言,衍生产品就是根据某些基础产品进行派生而来的产品,因此衍生产品的标的资产或者标的变量就是这些基础资产.比如,股票期权就是根据股票价格派生出的一种衍生产品.再如最近经常说的碳中和概念,其也有派生出的碳交易期货期权,其标的资产就是碳交易期货.
长话短说,期权就是一种合约,签订期权合约的交易者就拥有了一种权利,该合约赋予持有人在某一特定日期或该日之前的任何时间以固定价格购进或售出一种资产的权利.
那么,期权的概念了解以后,我们进一步来看期权的类型.联想一下,既然期权是基础资产的衍生产品,而基础资产,如股票,其价格多数时候都是曾献上涨或者下跌的情况,因此期权也可以分为看涨期权和看跌期权.其中,看涨期权持有者拥有在未来的一段时间内可以以某一特定价格买入某种资产的权利,看跌期权持有人拥有在未来的一段时间内可以以某一特定价格卖出某种资产的权利(很容易理解,既然是看涨,那持有者便认为标的资产未来的价格会更高,因此先约定以一个"合算"的价格在未来某一时间买入该资产,同理,看跌一样理解).
在了解期权的类型以后,需要知道期权合约中几个重要的变量或者要素.正如概念中所说的,“以某一特定价格”,这个特定价格通常被称为行权价或者执行价格(敲定价格),"特定时间"通常是到期日或者期限.说到期限,需要补充一点,欧式期权的持有人只有在到期日当天才可以选择是否行驶自己的权利,而美式期权则可以在到期日之前的任一交易日行使权力.
二、期权中的交易者
1.交易者类型
在期权交易过程中,根据交易者对未来行情的看法,可以分为四类:
(1)看涨期权买方:即买入看涨期权
(2)看涨期权卖方:即卖出看涨期权
(3)看跌期权买方:即买入看跌期权
(4)看跌期权卖方:即卖出看跌期权
计算公式为:
假定到期日的股票价格为ST,期权的执行价格为K(没有考虑成本)
欧式看涨期权的多头收益为:max(ST-K,0)
欧式看跌期权的多头收益为:max(K-ST,0)
欧式看涨期权的空头收益为:min(K-ST,0)
欧式看跌期权的空头收益为:min(ST-K,0)
以下为期权多空头收益代码,未考虑交易成本
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
K=8000
ST=np.linspace(7000,9000,100)
h=np.maximum(ST-K,0)
plt.figure()
plt.plot(ST,h,lw=2.5)
plt.xlabel('ST')
plt.ylabel('收益')
plt.title('看涨期权多头')
plt.grid(True)
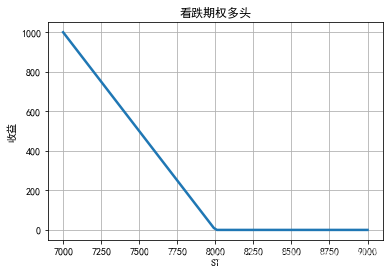
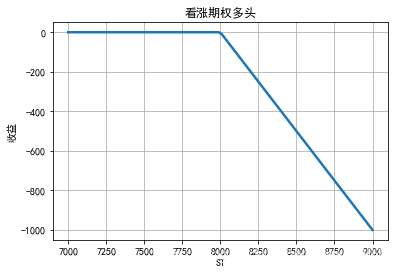

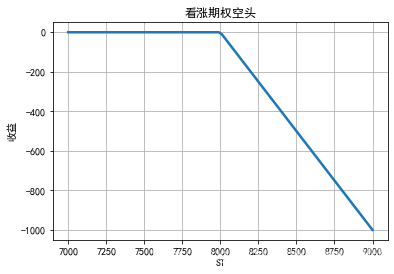
从以上的图中可以知道,期权买方的收益是无限大,亏损是一定的,期权卖方刚好相反.
这里可以思考一下,看涨期权买方和看跌期权卖方其对标的资产未来的价格表现其实是乐观的,看涨期权卖方和看跌期权买方对标的资产未来价格的看法是消极的.
行文至此,需要再补充一点,期权的买方被称为多头,期权的卖方被称为空头.对期权买方和卖方而言,其权利和义务是极端不对等的.期权买方在支付权利金以后便拥有权利,而没有义务(也就是说买方可以觉得自己是否行权,而没有任何义务),而卖方则相反,只有义务没有权利.
2.举(多)个栗子
那么期权作为衍生产品,为什么会具有如此的重要性,以至于学者和交易者对其兴趣极大?这里举几个例子进行简单的说明(附代码)
例1
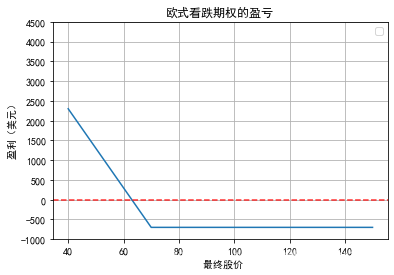
投资者买入执行价格为100美元、购买100股股票的看涨期权。假如股票的价格为98元,期权到期日为4个月,购买1股股票的期权价格为5美元。持有者的最初投资为500美元。期权为欧式期权,只能在到期日行权。假如到期时股票价格小于100美元,投资者不会行使权力,假如股票价格大于100美元,期权会被执行。假定到期时股票价格为115美元,通过行使期权权力,投资者可以挣得1500美元,除去最初的期权费用,投资者盈利为1000美元
以下代码展示了本例投资者买入看涨期权后的盈利与最终股票价格之间的关系.
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams["font.sans-serif"]=["SimHei"]
mpl.rcParams["axes.unicode_minus"]=False
S=98
K=100
ST=np.linspace(70,150,100)
X=5
H=np.maximum(ST-K,0)*100-X*100
plt.plot(ST,H)
plt.grid()
plt.title('欧式看涨期权的盈亏')
plt.axhline(0,color='r',linestyle="--",alpha=0.8)
plt.legend(loc=1)
plt.xlabel(' 最终股价')
plt.ylabel(' 盈利(美元)')
my_y_ticks = np.arange(-1000, 5000, 500)
plt.yticks(my_y_ticks)
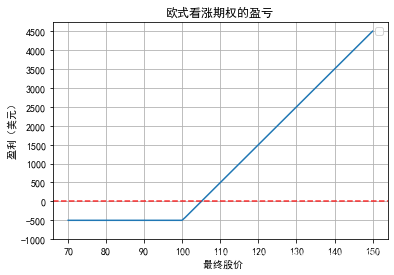
通过这幅图可以清楚的发现,当股价价格低于行权价时,持有者是不会行使权力的,那么他将损失一定的权利金,当股价高于行权价时,持有者会选择行权,这样起码可以减少损失(算上权利金)或者增加盈利.所以对于看涨期权的买方而言,其盈利是可以无限大的(股价无限上涨),而损失则是锁定的.
例2
看涨期权持有者希望股票价格上涨,而看跌期权持有者希望股票价格下跌.假设看跌期权的执行价格为70美元,以执行价出售100股股票的看跌期权,假定股票当前的价格为65美元,期权到期日为三个月,卖出一份看跌期权的费用为7美元. 投资者最初投资为700美元。欧式期权只有在到期日股票价格低于70美元时才会被行权,假定到期日时股票价格为55美元,投资者能以55美元买入100股股票,按照70美元卖出100股股票,所以投资者盈利为1500美元,减去最初的期权费用700美元,净盈利为800美元.以下代码为上述过程的可视化
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams["font.sans-serif"]=["SimHei"]
mpl.rcParams["axes.unicode_minus"]=False
S1=65
K1=70
ST1=np.linspace(40,150,100)
X1=7
H1=np.maximum(K1-ST1,0)*100-X1*100
plt.plot(ST1,H1)
plt.grid()
plt.title('欧式看跌期权的盈亏')
plt.axhline(0,color='r',linestyle="--",alpha=0.8)
plt.legend(loc=1)
plt.xlabel(' 最终股价')
plt.ylabel(' 盈利(美元)')
my_y_ticks = np.arange(-1000, 5000, 500)
plt.yticks(my_y_ticks)
通过图中可以清楚的看出,看跌期权的持有者在股价小于行权价时会选择行权,股价下跌越多时持有者的盈利越多,而股价上涨时其亏损也是锁定在一定成本之中的.
以上两个例子是分析期权买方的盈利的,而对于期权卖方,其盈利情况则刚好相反.
任何一个期权合约都有两方,一方为期权的多头,即期权的买入方,一方为期权的空头,即期权的卖出方。卖出期权的一方在最初收入期权费,但这一方在今后有潜在的义务,卖出期权的一方的盈亏与买入期权的一方的盈亏相反。 以下代码为期权的卖方盈亏情况.
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams["font.sans-serif"]=["SimHei"]
mpl.rcParams["axes.unicode_minus"]=False
S2=98
K2=100
ST2=np.linspace(70,150,10)
X2=5
H2=-np.maximum(ST2-K2,0)*100+X2*100
plt.plot(ST2,H2)
plt.grid()
plt.title('卖出看涨期权的盈亏')
plt.axhline(0,color='r',linestyle="--",alpha=0.8)
plt.legend(loc=1)
plt.xlabel(' 最终股价')
plt.ylabel(' 盈利(美元)')
my_y_ticks = np.arange(-5000, 1000, 500)
plt.yticks(my_y_ticks)
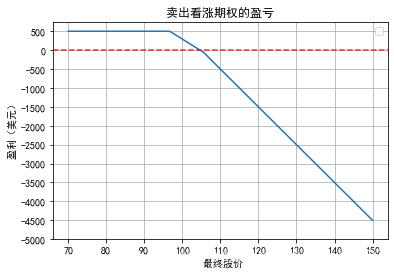
看涨期权的空头收益与看涨期权多头相反,当股价上涨时,其亏损会变大,而当股价下降时,其盈利是有限的.
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams["font.sans-serif"]=["SimHei"]
mpl.rcParams["axes.unicode_minus"]=False
S3=65
K3=70
ST3=np.linspace(40,150,100)
X3=7
H3=-np.maximum(-ST3+K3,0)*100+X3*100
plt.plot(ST3,H3)
plt.grid()
plt.title('卖出看跌期权的盈亏')
plt.axhline(0,color='r',linestyle="--",alpha=0.8)
plt.legend(loc=1)
plt.xlabel(' 最终股价')
plt.ylabel(' 盈利(美元)')
my_y_ticks = np.arange(-3000, 1000, 500)
plt.yticks(my_y_ticks)
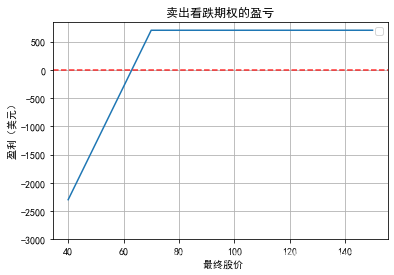
看跌期权空头则与看跌期权多头相反.当股价下跌时,其亏损加大,股价上涨时,其收益有限.
例3 采用期权对冲
投资者5月持有1000股价值28元的股票,投资者担心股票价格下跌,买入看跌期权进行对冲.
7月合约,买入10手看跌期权,期权执行价为27.5元,期权报价为1元,因此期权的持有成本为1000元
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
S=28
K=27.5
D=1000
ST=np.linspace(20,40,100)
h=ST*1000
H=np.maximum(K-ST,0)*1000-1000+ST*1000
plt.plot(ST,h,lw=2.5,color='r',linestyle='--',label='无对冲')
plt.plot(ST,H,lw=2.5,color='m',linestyle='-',label='有对冲')
plt.xlabel('股价(美元)')
plt.ylabel('持有者头寸价值(美元)')
plt.grid(True)
plt.legend(loc=0)
plt.title('证券组合在无对冲和有对冲情况下两个月后的价值')
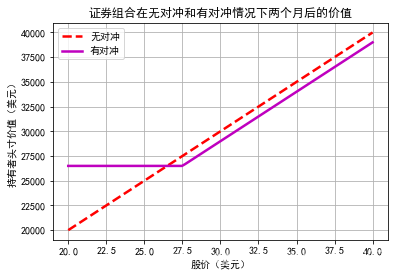
可以看出,对冲策略的交易成本为1000元,可以确保股票的卖出价格至少为27.5元(合约期限之内).如果到期时股价低于27.5元,则持有者会行驶权利,那么收入为27.5*1000-1000=26500元.如果到期日股价高于27.5元,持有者不行权,但是股价收益会更高.此外,对冲组合能够锁定收益最小值,效果明显由于无对冲的收益.
例4 投机
#利用期权进行投机.假设股票现在的价格为20美元,执行价格为22.5美元,期限为两个月的看涨期权的当前价格为1美元。
两中投机方式
1.买入100股股票
2.买入2000份看涨期权
假设1:股票两个月后上涨至27美元
假设2:股票两个月后下降至15美元
投机收益情况如下
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from matplotlib import pyplot as plt
import matplotlib
matplotlib.rc("font",family='DengXian')
S=20
K=22.5
ST=np.linspace(10,40,100)
h=100*(ST-20)
H=np.maximum(ST-K,0)*2000-2000
plt.plot(ST,h,lw=2.5,color='r',linestyle='--',label='买入股票')
plt.plot(ST,H,lw=2.5,color='m',linestyle='-',label='买入期权')
plt.xlabel('股价(美元)')
plt.ylabel('利润(美元)')
plt.grid(True)
plt.legend(loc=0)
plt.title('对价格为20美元的股票的两种投机策略的盈亏')
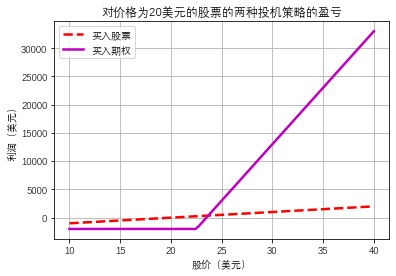
通过图中可知,期权策略可能会引起比股票策略更大的损失,但是也能够获得比股票策略更高的收益.这也说明期权能够提供一种杠杆效应.
总结
这是本系列的第一篇博文,主要是介绍了期权的基本概念,以及期权交易的基础知识,接下来会对期权的交易策略进行介绍.
第二章
前言
本章中,我们将以股票期权为例,介绍影响期权价格的因素,并且通过python进行量化实现。
一、影响期权价格的因素
1.初识BS模型
在这里,我们会想,要说影响期权价格的因素,首先需要有一个具体的公式或者指标来对期权价格进行才对,有了具体的公式和指标,就可以知道影响价格的因素,并且知道这些因素和价格之间的具体影响,比如是正相关还是负相关,抑或是先正后负等等。所以,我们先直观的给出一个期权定价最为经典的计算公式:于 Black-Scholes微分 方 程(B-S微分方程)。
传统理论认为期权的标的资产价格Pt 遵循几何布朗运动,并且期权的价格是时间与股票价格的函数,即Gt=G(Pt,t)。根据伊藤引理与无套利假设,Black等在求 解 B-S微分 方 程 的基础上得到如下BS欧式期权定价模型(不考虑股息,即股息d=0):(具体的BS公式留到后面的篇章再细说)
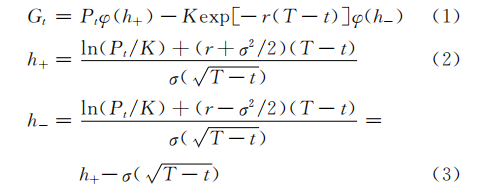
这里对式子的字母进行说明,Gt为看涨期权的价格;Pt为标的资产的价格;K 为交割价格;φ(x)为标准正态分布函数在x处的取值;T-t为距离到期日的时间间隔;r为无风险利率;σ为标的资产价格的波动率。
2.影响因素
从这些计算公式中可以直观的看出,期权价格与Pt,K,T,t,σ,r等数值密切相关,因此,我们可以认为,影响期权价格的因素主要有以下6个:(考虑股息,若剔除股息,则为5个)。
**(1)**当前股票价格Pt
**(2)**执行价格K
**(3)**期权到期期限T-t
**(4)**股票价格波动率σ
**(5)**无风险利率r
**(6)**股票期权期限内支付的股息d
二、python实践环节
这一部分,我们将对上述的六个影响因素进行说明。
1.股票价格
对看涨期权而言,如果期权进行交割,那么期权的收益就等于股票价格与期权执行价格之差(不考虑交易成本):Pt-K.可以看出,当K一定时,Pt越大,收益越高,看涨期权的价格也就越高。对于看跌期权而言,看跌期权的收益等于期权执行价格减去股票价格,即K-Pt,可知股票价格上涨时,看跌期权的收益会减小,因此看跌期权的价格也会下跌。由此,我们可以直观的感受到,股票价格对看涨期权价格而言是正相关,对看跌期权价格而言是负相关。
代码实现:
from pylab import plt
plt.style.use('seaborn')
%matplotlib inline
import math
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from scipy.integrate import quad
mpl.rcParams['font.family'] = 'serif'
#
# Helper Functions
#
def dN(x):
''' Probability density function of standard normal random variable x. ''' #标准正态随机变量 x 的概率密度函数
return math.exp(-0.5 * x ** 2) / math.sqrt(2 * math.pi)
def N(d):
''' Cumulative density function of standard normal random variable x. '''
return quad(lambda x: dN(x), -20, d, limit=50)[0]
def d1f(St, K, t, T, r, sigma):#设置函数d1
''' Black-Scholes-Merton d1 function.
Parameters see e.g. BSM_call_value function. '''
d1 = (math.log(St / K) + (r + 0.5 * sigma ** 2)* (T - t)) / (sigma * math.sqrt(T - t))
return d1
#
# Valuation Functions
#
#欧式看涨期权函数
def BSM_call_value(St, K, t, T, r, sigma):
''' Calculates Black-Scholes-Merton European call option value.
Parameters
==========
St : float
stock/index level at time t
K : float
strike price
t : float
valuation date
T : float
date of maturity/time-to-maturity if t = 0; T > t
r : float
constant, risk-less short rate
sigma : float
volatility
Returns
=======
call_value : float
European call present value at t
'''
d1 = d1f(St, K, t, T, r, sigma)
d2 = d1 - sigma * math.sqrt(T - t)
call_value = St * N(d1) - math.exp(-r * (T - t)) * K * N(d2)
return call_value
#欧式看跌期权函数
def BSM_put_value(St, K, t, T, r, sigma):
''' Calculates Black-Scholes-Merton European put option value.
Parameters
==========
St : float
stock/index level at time t
K : float
strike price
t : float
valuation date
T : float
date of maturity/time-to-maturity if t = 0; T > t
r : float
constant, risk-less short rate
sigma : float
volatility
Returns
=======
put_value : float
European put present value at t
'''
put_value = BSM_call_value(St, K, t, T, r, sigma) \
- St + math.exp(-r * (T - t)) * K
return put_value
# Model Parameters
#
points=100
St =2.72 # 50ETF value
K = 2.7 # option strike
t = 0.0 # valuation date
T = 1.0 # maturity date
r = 0.015 # risk-less short rate
sigma = 0.2 # volatility
# C(K) plot现值与股票价格的关系
plt.figure(figsize=(10,8))
slist = np.linspace(2.7, 3, points)
vlist_call = [BSM_call_value(St, K, t, T, r, sigma) for St in slist]
vlist_put = [BSM_put_value(St, K, t, T, r, sigma) for St in slist]
plt.plot(slist, vlist_call,'r',label='call')
plt.plot(slist, vlist_put,'g',label='put')
plt.grid(True)
plt.xlabel('stock price')
plt.ylabel('present value')

2.执行价格
执行价格的分析和股票价格分析紧密相关,回想一下,对看涨期权而言,如果期权进行交割,那么期权的收益就等于股票价格与期权执行价格之差(不考虑交易成本):Pt-K.可以看出,当Pt一定时,K越大,收益越低,看涨期权的价格也就越低。对于看跌期权而言,看跌期权的收益等于期权执行价格减去股票价格,即K-Pt,可知执行价格变大时,看跌期权的收益会增加,因此看跌期权的价格也会上升。由此,我们可以直观的感受到,执行价格对看涨期权价格而言是负相关,对看跌期权价格而言是正相关。
代码如下
# C(K) plot现值与执行价的关系
plt.figure(figsize=(10,8))
plt.figure(figsize=(10,8))
klist = np.linspace(2.2, 3, points)
vlist_call = [BSM_call_value(St, K, t, T, r, sigma) for K in klist]
vlist_put = [BSM_put_value(St, K, t, T, r, sigma) for K in klist]
plt.plot(klist, vlist_call,'r',label='call')
plt.plot(klist, vlist_put,'g',label='put')
plt.grid(True)
plt.xlabel('strike price')
plt.ylabel('present value')
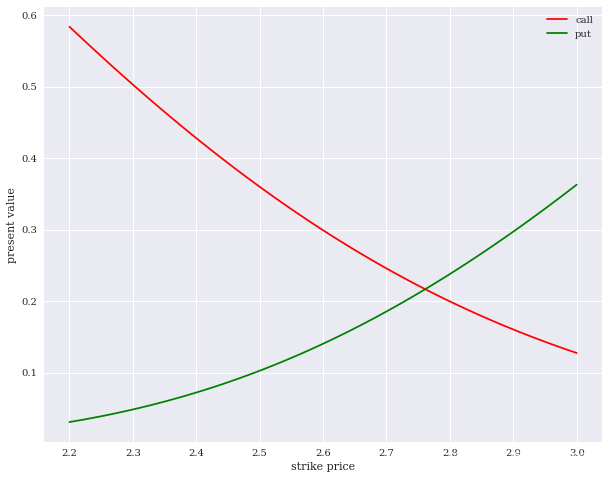
3.期权到期期限
从公式可看出,随时到期期限的增加,看涨期权和看跌期权的价格都会增加。从图中可以看出,同等情况下,看涨期权价格的增加程度更大一些。
代码如下:
# C(T) plot现值与到期时间的关系
plt.figure(figsize=(10,8))
tlist = np.linspace(0, 1, points)
vlist_call = [BSM_call_value(St, K, t, T, r, sigma) for T in tlist]
vlist_put = [BSM_put_value(St, K, t, T, r, sigma) for T in tlist]
plt.plot(tlist, vlist_call,'r',label='call')
plt.plot(tlist, vlist_put,'g',label='put')
plt.grid(True)
plt.legend()
plt.grid(True)
plt.xlabel('maturity')
plt.ylabel('present value')
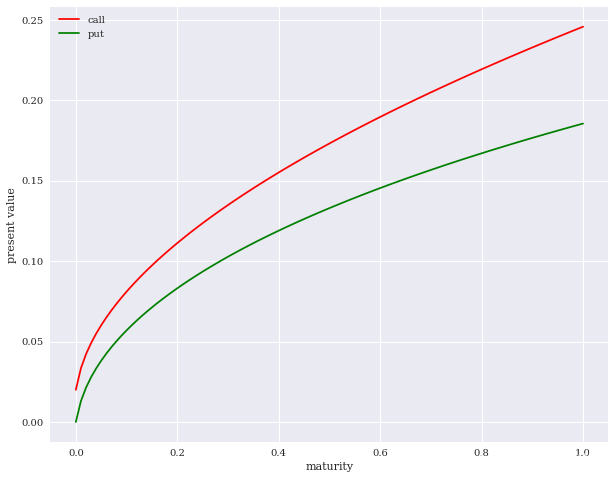
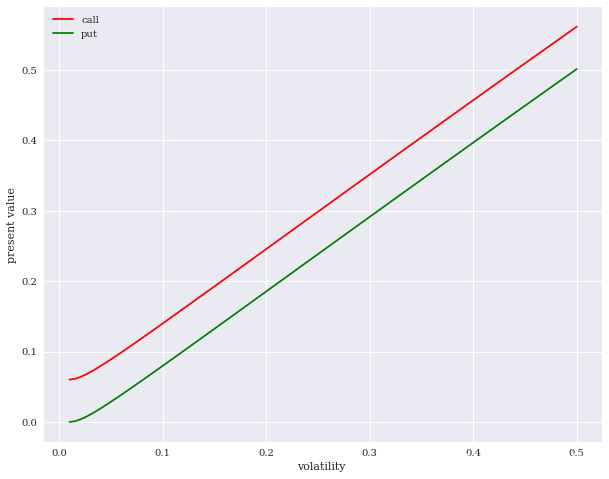
4.波动率
同理,从公式可看出,随时波动率的增加,看涨期权和看跌期权的价格都会增加。从图中可以看出,同等情况下,看涨期权价格的增加程度更大一些。
# C(sigma) plot现值与波动率的关系
plt.figure(figsize=(10,8))
slist = np.linspace(0.01, 0.5, points)
vlist_call = [BSM_call_value(St, K, t, T, r, sigma) for sigma in slist]
vlist_put = [BSM_put_value(St, K, t, T, r, sigma) for sigma in slist]
plt.plot(slist, vlist_call,'r',label='call')
plt.plot(slist, vlist_put,'g',label='put')
plt.legend()
plt.grid(True)
plt.xlabel('volatility ')
plt.ylabel('present value')
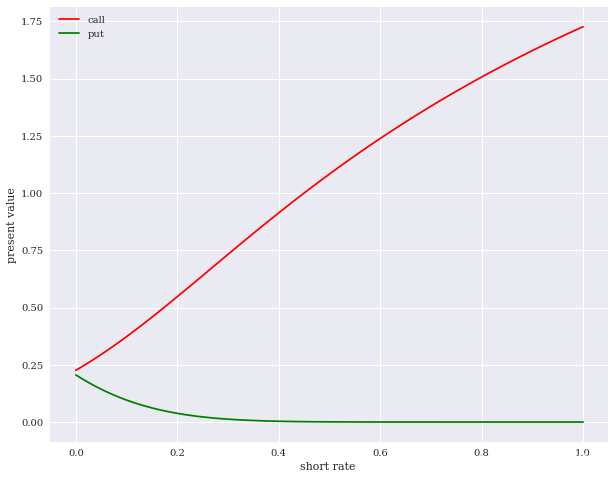
5.无风险利率
无风险利率相对而言,对期权价格的影响没有那么大,当无风险利率增加时,代表着投资者对股票收益的期望值也会增加,同时又会让期权持有者未来收到的现金流贴现值降低,综合而言,看涨期权的价格会上涨,看跌期权的价格会下跌。
代码如下:
# C(r) plot现值与短期利率的关系
plt.figure(figsize=(10,8))
rlist = np.linspace(0, 1, points)
vlist_call = [BSM_call_value(St, K, t, T, r, sigma) for r in rlist]
vlist_put = [BSM_put_value(St, K, t, T, r, sigma) for r in rlist]
plt.plot(rlist, vlist_call,'r',label='call')
plt.plot(rlist, vlist_put,'g',label='put')
plt.legend()
plt.grid(True)
plt.xlabel('short rate ')
plt.ylabel('present value')
6.股息
这里没有给出带有股息的计算公式(后文会讲述),所以这里直接给出结论,看涨期权价格与股息大小成负相关关系,看跌期权价格与股息大小成正相关关系。
代码:后文补上
总结
第二章的总结如下,稍微划水一下直接粘了书上的图片。
