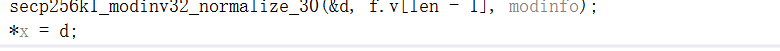2021SC@SDUSC
本篇博客是上一篇的延续，上一篇太长了，拆开两篇来写。也是模块反演的libsecp256k1代码实现内容
计算30个步骤（可变时间）的转移矩阵和eta。
输入：eta：初始eta
f0：初始f的底边
g0：初始g的底边
输出：t：转移矩阵
返回：最终预计到达时间
实现解释中的divsteps\u n\u matrix\u var函数
变换矩阵
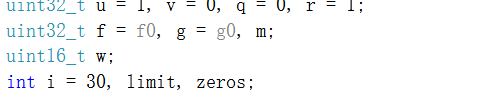一次执行零步；它们都只是把g除以2
如果eta为负值，则将其取反，并将f，g替换为g，-f
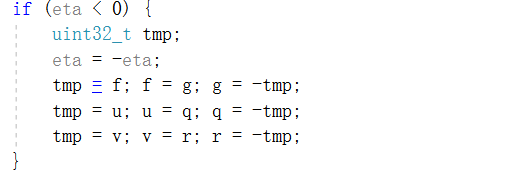
预计到达时间现在大于等于0。在接下来的内容中，我们将抵消g的底部位。不超过我可以被取消（正如我们在那一点之前所做的），也不超过eta+1可以被取消，因为一旦发生这种情况，它的标志将翻转。
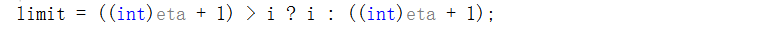m是底部最小（限制，8）位的掩码（我们的表只支持8位）。
找出必须将f的倍数添加到g以取消其底部最小值。
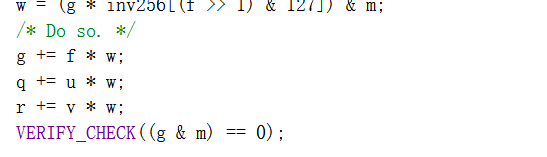返回t中的数据和返回值。
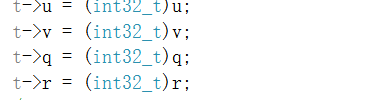
t的行列式必须是二的幂。这保证了与t相乘不会改变f和g的gcd，除了增加一个2的幂因子（将再次除以）。由于每个步骤的单个矩阵都有行列式2，因此其中30个步骤的总和将有行列式2^30。
计算（t/2^30）* [d，e]模，其中t是30步的转移矩阵。在输入和输出上，d和e在范围内（-2模，模）。所有输出分支将在范围（-2^ 30,2^30）内。这将实现解释中的update_de 功能。
[md，me]以零开始；如果d为负，则加上[u，q]；如果e为负，则加上[v，r]。
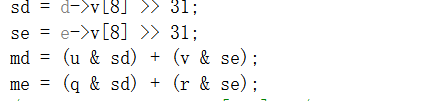开始计算t[d，e]
修正md，me，使t*[d，e]+模*[md，me]有30个零底位
更新t*[d，e]+模*[md，me]的计算开始，现在已知md，me。
验证计算的低30位是否确实为零，然后将其丢弃。
现在迭代计算t*[d，e]+模*[md，me]的分支i=1…8，并将它们存储在输出分支i-1中（下移30位）。
剩下的是t*[d，e]+模*[md，me]的9；将其存储为输出8。
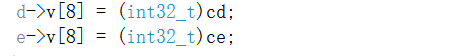
计算（t/2^30）*[f，g]，其中t是30个步骤的转移矩阵。这实现了解释中的update_fg函数。
开始计算t*[f，g]。
验证结果的底部30位是否为零，然后将其丢弃。
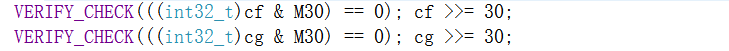
现在迭代计算t*[f，g]的分支i=1…8，并将它们存储在输出分支i-1中（下移30位）。
计算（t/2^30）[f，g]，其中t是30步的转移矩阵。在f和g中对可变数量肢体进行操作的版本。此版本实现modinv64_impl.h中说明中的更新功能。
开始计算t[f，g]。
验证结果的底部62位是否为零，然后将其丢弃。
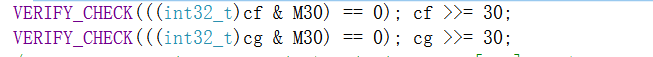现在迭代计算t*[f，g]的分支i=1…len，并将它们存储在输出分支i-1中（下移30位）
计算x模modinfo->module的倒数，并用它替换x（x中的常数时间）。
进行20次迭代，每次迭代30个步骤=600个步骤。590足以支持256位输入。计算30步后的转移矩阵和新zeta
使用该转移矩阵更新d，e
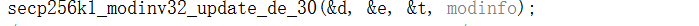
在这一点上，已经进行了足够的迭代，g必须达到0，并且（如果g最初不是0）f现在必须等于初始f的+/-GCD，g值即+/-1，并且d现在包含+/-模逆
可选地对d求反，规格化为[0，模数），然后返回它。
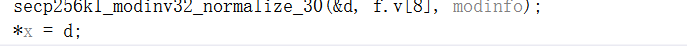计算x模modinfo->module的倒数，并用它替换x（可变时间）
每次迭代30步，直到g=0；计算30步后的转移矩阵和新eta；使用该转移矩阵更新d，e；使用该转移矩阵更新f，g。
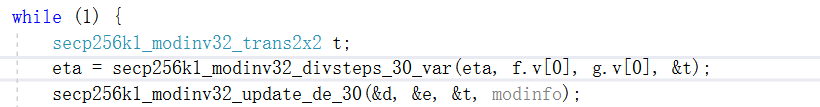如果g的分支为0，则有可能g=0，检查所有其他肢体是否也为0；如果是这样，我们就结束了
确定len>1以及f和g的分支（len-1）是0还是-1
此时g为0，并且（如果g最初不是0）f现在必须等于初始f的+/-GCD，g值即+/-1，并且d现在包含+/-1模逆。
可选地对d求反，规格化为[0，模数），然后返回它。
