2021SC@SDUSC
参考stackoverflow的博客、《Faster batch forgery identification》
ecmult的作用是可以加快aP+bG形式的运算，可以提高签名验证、公钥恢复的效率。
ecmult加速计算aP+bG
目录
Strauss-Shamir方法进行EC标量乘法
该算法通过递归计算ba1/2ccP1+ba2/2ccP2+·······+ban/2ccPn，将c倍，然后添加预计算量（a1 mod2c）P1+（a2mod 2c）P2+···+（anmod 2c）Pn。这里2c是由算法选择的基数；例如，对于256位标量，c=5是合理的。我们跳过了对标准加速比（如有符号数字）的讨论。该算法不能很好地扩展到n的大值（因为它涉及太多的预计算，即使对于c=1），但标准变量可以很好地扩展到n的大值：在最后一步，一个变量添加单独的预计算量（a1mod 2c）P1，（a2mod 2c）P2，显然，我们可以将这些预先计算的量重新用于后续涉及P1，…，Pm的多标量乘法，使用相同的c选项。此外，如果在每个步骤中从左到右添加预计算的量，则中间结果之一正好是（a1mod 2c）P1+·····+（ammod 2c）Pm。这大大降低了当m较大时计算a1P1+····+amPm的成本：递归的每个步骤都从成本c+m（c加倍和m添加）下降降到c+1。
这是一种在log 2 （ k ）加法和加倍中计算k1 · P + k2 · Q的方法，其中k1, k2 < k
要将数字P乘以n位标量k ，可以根据k的二进制展开使用加倍和加法。 假设k = 9 。 在二进制中，那是1001 ，你可以像这样计算9P ：
R=0
R=R2+P //the most significant ‘1’ bit
R=R2 //next bit is 0
R=R2 //next bit is 0
R=R2+P //next bit is 1
Strauss-Shamir技巧只是通过在链内而不是外部进行加法来计算aP + bQ 。 让我们说，在二进制中， a=1001和
b = 0011。 然后我们就这样做：
R=0
R=R2+P //bits from a,b = 1,0
R=R2 //bits from a,b = 0,0
R=R2+Q //bits from a,b = 0,1
R=R2+P+Q //bits from a,b = 1,1
如果预先计算P + Q ，那么这不会比单个乘法花费更长的时间。
Pippeneger算法
作为一个更先进的例子，考虑Pippenger的多标量乘方法。Pippenger的方法不像Straus方法那样简单，但是当有许多大标量时，它的速度要快得多。在某些情况下，它的速度几乎是原来的两倍，并且在最佳速度的1+o（1）范围内
更快的批量伪造识别基本上是所有标量序列。选择基数2c，并按照Straus的算法进行，但将最后一步替换为以下计算。根据a1 mod 2c、a2 mod 2c、…、an mod 2c的值，将点P1、P2、…、Pn排序为2c bucket。丢弃存储桶0并在剩余存储桶中添加点，获得总和S1、…、S2c?1.现在计算（a1mod 2c）P1+··+（an mod 2c）Pn=S1+2S2+··+（2c?1） S2c?1.
作为中间量S2c-1的总和，S2c?1+S2c?2，…，S2c?1+S2c?2+···+S1。观察以相同方式计算a1P1+···+amPm，使用相同的c值，将P1、P2、…、Pm放入完全相同的桶中。如果对于a1P1+···+anPn计算，我们小心地从左到右在每个桶中添加点，则P1、P2、…、Pm之后的中间结果将恰好是与a1P1+··+amPm相关的总和。对于典型参数，每个桶中有几个点，因此该方法比标准计算a1P1+·+amPm快几倍。如前所述，最好改变顺序，在每个bucket中添加点，递归地添加来自P1、P2、…、Pm的点和来自Pm+1、…、Pn的点
libsecp256k1代码分析
对于较大的ECMULT_WINDOW_SIZE值，该代码可能是正确的，但这没有经过测试。已知以下限制，可能还有更多限制：如果窗口>27且大小为32位，则代码不正确，因为我们分配的内存对象的大小（以字节为单位）不适合大小。
如果WINDOW_G>31且int有32位，则代码不正确，因为某些表达式将溢出。
ECMULT_WINDOW_SIZE的值越大，性能可能会越好，但代价是预计算表的数量会成倍增加。确切的tablea尺寸是
（1<<（WINDOW_G2））*sizeof（secp256k1_ge_storage）字节，其中sizeof（secp256k1_ge_storage）通常为64字节，但由于平台特定的填充和对齐，可以更大。使用了两个此大小的表（由于自同态优化）。
具有预计算倍数的表需要具有的条目数
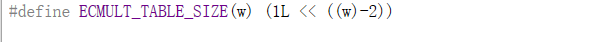
多重乘法：R=inp_g_scg+sum_i niAi。为给定的点数和暂存空间大小选择正确的算法。重置并覆盖给定的暂存空间。如果这些点不适合暂存空间，则该算法将使用成批的点重复运行。如果没有给出划痕空间，则使用一个简单的算法，将点与相应的标量相乘并相加。
返回：
成功时为1（包括inp_g_sc为空且n为0时）
如果没有足够的划痕空间容纳单个点或点，则为0
回调返回0
ecmult_multi算法的暂存空间上分配的对象数
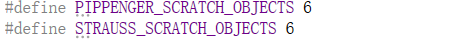pippenger_wnaf比strauss wnaf快的最小点数
用预先计算的a的奇数倍数填充表格“prej”。Prej将包含值[1a，3a，…（2*n-1）*a]，因此它将为n个值留出空间。zr[0]将包含prej[0]。z/a.z。其他zr[i]值=prej[i]。z/prej[i-1]。z.prej的z值未定义，但最后一个值除外。
在“d”是仿射的同构上执行加法：删除“d”的z坐标，缩放1P起始值的x/y坐标，而不更改其z。
“prej”中的每个点的z坐标都太小，其系数为“d.z”。不过，实际上只使用了最后一点的z坐标，所以只需更新该坐标即可。
用预先计算的a的奇数倍数填写“pre”表。结果点集被带到单个常量Z分母，将X和Y坐标作为ge_storage点存储在pre中，并将全局Z存储在rz中。它仅对大小为WINDOW_a wnaf倍数的表进行操作。要计算aP+bG，我们使用此函数计算P的表，并对g使用<ecmult\u static\u pre\u g.h>中的预计算表。
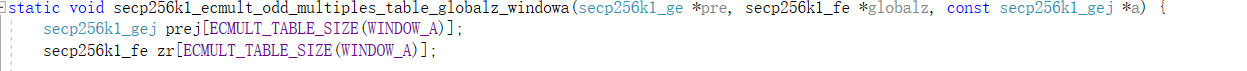计算雅可比形式的奇数倍数。
将它们带到相同的Z分母。
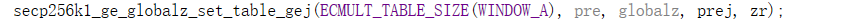以下两个宏从预先计算的倍数表中检索特定的奇数倍数
将数字转换为WNAF表示法。数字由总和（2^i*wnaf[i]，i=0…bit）表示，并具有以下保证：
-每个wnaf[i]要么是0，要么是介于（1<<（w-1）-1）和（1<<（w-1）-1）之间的奇数整数
-wnaf中的两个非零条目至少由w-1个零分隔。
-返回wnaf中的设置值数。该数字最多为256，且最多比输入（绝对值）中的位数多一位。
WNAF转换
分裂G因子
分为na_1和na_lam（其中na=na_1+na_lam*lambda，na_1和na_lam约为128位）
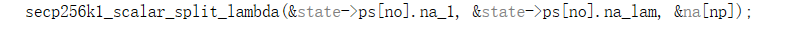为na_1和na_lam构建wnaf表示。
计算a的奇数倍数。所有倍数都被带到相同的Z’分母’，该分母存储在Z中。由于secp256k1’同构，我们可以假装Z坐标为1进行所有操作，使用仿射加法公式，并在最后更正结果的Z坐标一次。例外是预计算的G表点，它们实际上是仿射的。与用于其他点的基相比，它们的Z比为1/Z，因此我们可以使用secp256k1_gej_add_zinv_var，它使用相同的同构有效地与已知的Z逆相加。
计算雅可比形式的奇数倍数。
将它们带到相同的Z分母
将ng拆分为ng_1和ng_128（其中gn=gn_1+gn_128*2^128，gn_1和gn_128为~128位）
为ng_1和ng_128构建wnaf表示
定义划痕空间函数
secp256k1_ecmult_multi_func接口的包装器
将数字转换为WNAF表示法。该数字由总（2^{wi}*WNAF[i]，i=0…WNAF_SIZE（w）+1）-返回值表示。
它有以下保证：
-每个wnaf[i]要么是0，要么是介于-（1<<w）和（1<<w）之间的奇数整数
-字数集始终为WNAF_大小（w）
-返回的倾斜为0或1
计算最后的窗口大小。当窗口大小不除以标量中的位数时相关。
将第一个非零字的位置存储在max_pos中，以便在计算wnaf时跳过前导零。
如果系数为1或-1，则将其设置为零，并且前面的数字分别严格为负或严格为正。因为上面的代码假设wnaf[pos-1]是奇数的，所以只改变先前位置的系数。
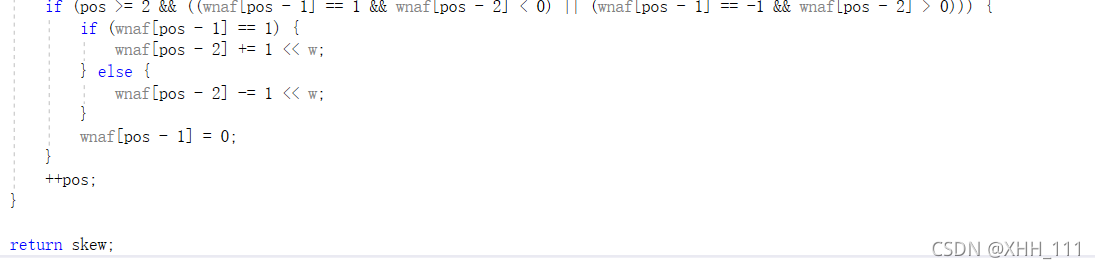
pippenger_wnaf将多点乘法的结果计算为
如下：标量被带到wnaf中，每个都有n_wnaf元素。然后，对于每个i<n_wnaf，首先将每个点添加到对应于该点的wnaf[i]的“bucket”。其次，将桶添加到一起，以便 r += 1bucket[0] + 3bucket[1] + 5*bucket[2] + …
针对wnaf倾斜进行校正
累加总和：桶[0]+3桶[1]+5桶[2]+7桶[3]+…=桶[0]+桶[1]+桶[2]+桶[3]+…+2（桶[1]+2桶[2]+3桶[3]+…）
使用中间运行和：
正在运行的_sum=bucket[0]+bucket[1]+bucket[2]+…
通过延迟（r）的最终窗口倍增来隐式完成倍增。
返回给定点数的最佳bucket_窗口（由一组bucket表示的标量的位数）。
返回bucket_窗口的最大最佳点数。
返回给定数量的点（不包括基点G）所需的划痕大小，而不考虑对齐。
当计算批量大小时，使用2（n+1）和自同态。+1的原因是我们将G标量添加到其他标量的列表中。
处理完成后，清除数据
返回除G外，可用于给定划痕空间的最大点数。该功能可确保使用更少的点。
更大的bucket_window可能支持更多点。但是，如果我们选择该选项，那么调用方就不能安全地使用任何小于该函数返回值的数字
通过简单地将每个点相乘和相加来计算ecmult_multi。
r = inp_g_scG
r += scalarpoint
根据最大批量和总点数，计算批量数量和批量大小
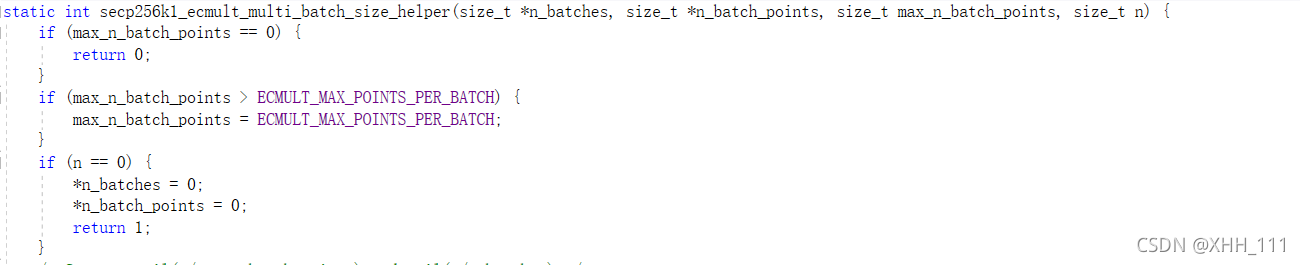
计算ceil（n/max\n\u批次点）和ceil（n/n\u批次）
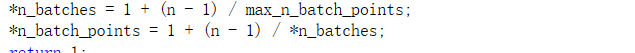在给定划痕空间的情况下，计算Pippenger算法的批量大小。如果大于阈值，则使用Pippenger算法。否则使用Strauss算法。作为第一步，检查是否有足够的空间用于Pippenger的algo（比Strauss的algo需要更少的空间），如果没有，使用简单的算法。
