前言
前文《天冷了,干了这碗“零知识证明”鸡汤》对「零知识证明学习」作了一个形象化的比喻:炖鸡汤。那么本系列的主要内容可以简单概括为《论高压锅炖鸡汤的一百种方法》之方法二。在学会了“清炖鸡汤”之后,不如来一口“阿胶鸡汤”补补脑细胞吧!
正如鸡汤不同风味之间各具千秋,不同的zk-SNARK方案也各有所长。zk-SNARK方案可以被分为【通用】与【非通用】zk-SNARK,PLONK与Groth16分别是其中的典型代表。通过本系列,我们将对PLONK算法内容作简要介绍,并指出PLONK和Groth16算法思路上的异同。
PLONK算法在[1]中提出,由来自于Protocol Labs的研究员Gabizon和以太坊隐私交易协议 Aztec Protocol 的两名研究人员合作完成。PLONK的提出晚于Groth16,在证明和验证的性能上与Groth16也存在一定差距,但是基于通用可更新的可信设置这一特点,使PLONK算法在零知识证明领域占据了一席之地。
可信设置
可信设置可以说是PLONK和Groth16两者间最显著的差异。正是为了避免一次性的可信设置,PLONK设计了后续的约束系统和问题压缩方式。那么什么是零知识证明中的可信设置呢?可信设置实际上是在创建一个用于证明验证的秘密,任何知道这个秘密的人都可以伪造证明通过验证。如果将零知识证明看作是一扇挡在证明者a和验证者b之间上锁的门,那么合法构建的证明就是可以打开门的口令,a提供口令即可进入房间。但是如果a得知了门的秘密也就是房间窗户的位置,那么a可以直接无视锁的存在翻窗进入房间。
▲无窗的房间(无需可信设置的零知识证明)
显然,最安全的做法是找一个「没有窗的房间」,这也是一部分零知识证明方案的思路——无需可信设置,例如可扩展透明知识论证zk-STARKs和防弹证明Bulletproofs。虽然它们的安全性得到提高,但是目前这类方法的证明验证性能是远低于zk-SNARKs的,近线性的验证和规模较大的证明(proof)使其不适用于很多场景。
▲窗户位置指定策略(基于可信设置的零知识证明)
PLONK和Groth16的做法都是保留窗户,但是尽力保护窗户的位置不被别人知道。
Groth16的做法是:根据不同的问题,每次都指定窗户在房间中的摆放位置,也就是它需要一次性的可信设置。
而PLONK面对不同的问题时:窗户的位置是固定不变的,即窗户的位置只需要被指定一次。也就是说PLONK的可信设置是通用的。
那么这些窗户指定的位置由谁来确定呢?当然,可信第三方是一个备选项。但这意味着说这间房间是否会被恶意证明者攻破,其安全性寄希望于这位第三方。除此之外还有一项热门技术也可为其提供思路——多方安全计算(MPC)。沿用之前的例子,可以不太严谨地将MPC概括为:多个人共同指定窗户的位置,除非这些参与者全部联合起来对答案,这个位置将无法由任何人得知。
显然,使用MPC时,参与者的数量越多,秘密的安全性越高,这类可信设置也比可信第三方更为用户所接受。遗憾的是,虽然目前提出了基于Groth16的可信设置[2],但是由于Groth16的秘密计算与特定的问题相关联,每次遇到新的问题时,必须重新开启一轮MPC可信设置。可想而知,需要多方参与的计算协议将是极为繁琐的,这样将大大影响Groth16的性能。相比之下,具备通用性的PLONK与MPC的适配度极高。
而之前提到的PLONK可信设置的可更新性则是指:通用的PLONK秘密可以通过再开启一轮MPC作更新。新生成的秘密安全性建立在两次MPC的安全性上,只要两次中有一个参与者是诚实的,这个秘密就是可信的。
约束系统
Groth16及PLONK均将程序(NP问题)先转化为一个由加法门和乘法门组成的算术电路,再通过将电路构建为多项式的形式来进行后续的计算。本节我们将使用Vitalik文章[3]中的一个简单例子进行说明:
对于程序qeval, prover需要证明自己知道qeval(x)=35的解,即x=3。
def qeval(x):
y = x**3
return x + y + 5 ,其转化为算术电路可表示如下:

PLONK中,上图电路的描述由两部分组成:门约束与线约束(copy constraints)。门约束固定电路中每个门的动作。此外,在电路中我们规定相连线的值应保持一致(例如a1=b1),对此线约束规定这些线的关系。接下来我们分别讨论两类约束的多项式表示。
门约束
在PLONK中,对于第i个门,可被描述为如下形式:
(QLi)ai+(QRi)bi+(QOi)ci+(QMi)aibi+Qci=0
其中Q均为常数,a, b, c则是信号的下标。具体地,在PLONK中门约束可以被分为三类:算术约束(加法门和乘法门)、布尔约束、公共输入约束。
【算术约束】最为常见,用于表示电路中的所有加法门和乘法门,此时a,b,c分别表示门的左右输入和输出信号下标,Q_C一般为0。根据门的类型剩余的符号有不同的取值:
加法门:QLi=1,QRi=1,QOi=-1,QMi=0
ai+bi-ci=0
乘法门:QLi=0,QRi=0,QOi=-1,QMi=1
-ci+ aibi=0
【布尔约束】顾名思义,用于约束布尔类型的信号,其值只能取0或1。例如现在需要约束下标为j的信号∈{0, 1},那么门约束式子中各变量的取值为:
ai=bi=j,QLi=-1,QMi=1,QOi=QRi=Qci=0
-j+j*j=0
另外,针对问题中出现的证明方和验证方都知道取值的输入(公共输入),需要在约束系统中有所体现。例如要求约束下标j的信号取值为v,对应的取值为:
ai=j,QLi=1,QMi=QOi=QOi=0,Qci=-v
j-v=0
利用该式,我们可以很容易地表示上图中的所有门约束:

与Groth16类似,可以将所有的多项式组整合在一个多项式中:

线约束
线约束可以分为两种情况:
同一多项式内部,例如:a1=a3
不同多项式之间,例如:a1=b1
当只需要考虑情况1时,可以通过构造p(x)=P(x)来实现约束:
X(X)=X
p(X+1)=p(X)(βX(X))+Y(X)+γ)
P(X+1)=P(X)(βX(σ(X))+Y(X)+γ)
p(0)=P(0)=1
其中β,γ为随机数,X->Y表示了待约束的多项式(例如: x-> a(x) ),P(x)使用了x的置换σ(x)。对于下面例子:
X(1) → Y(1)
X →Y:X(2) → Y(2) and,Y(1)=Y(3)
X(3) → Y(3)
σ(1)=3
σ(X):σ(2)=2
σ(3)=1
当且仅当Y(1)=Y(3)成立时,p(x)=P(x)。
现在,让我们增加问题的复杂度:需要约束的多项式个数为k时(仍然只考虑情况1)。自然地,设门的总数为n,我们可以对第j个多项式构造对应的p_j(x)=P_j(x),即
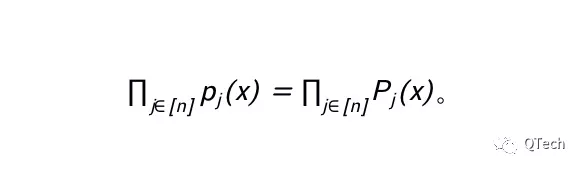
进一步地,情况2的出现要求对以下情况中的x作区分:
pj(x) and pi(x) (i不等于j,i,j∈[ n ])
那么可以增加对x的映射,对于第j个多项式:
X(X)=(j-1)n+X
p(X+1)=p(X)(βX(X))+Y(X)+γ)
P(X+1)=P(X)(β*X(σ(X))+Y(X)+γ)
p(0)=P(0)=1
以上就是线约束的全部内容,其实质是为了保证电路中同一条或相连线上的值相等。
与Groth16类似,将上述的约束联立将得到一个完整的PLONK约束系统。通过将抽象的代码和电路转化为约束系统R1CS,我们可以将一个零知识证明问题固定下来。让我们带着问题进入下篇:PLONK中如何将R1CS转为多项式描述?它与Groth16做法区别在何处?敬请期待!
参考文献:
[1] Ariel Gabizon and Zachary J. Williamson and Oana Ciobotaru. (2019). PLONK: Permutations over Lagrange-bases for Oecumenical Noninteractive arguments of Knowledge.
[2] Sean Bowe and Ariel Gabizon and Ian Miers. (2017). Scalable Multi-party Computation for zk-SNARK Parameters in the Random Beacon Model.
[3] https://vitalik.ca/general/2019/09/22/plonk.html