[区块链]【区块链】一文了解区块链原理

1 数字货币

什么是比特币？

1.1 诞生时间

2008年11月1日，中本聪发表比特币白皮书，提出一种点对点的、去中心化的数字交易系统。

比特币白皮书：Bitcoin:A Peer-to-Peer Electronic Cash
System

2009年比特币网络诞生中本聪创造了第一个比特币区块。

1.2 特点：去中心化的电子记账系统

去中心化的电子记账系统：不依赖任何一个中心记账，没有中央银行，而是由所有人一起来维护一个账本，任何人都可以去抢记账权。

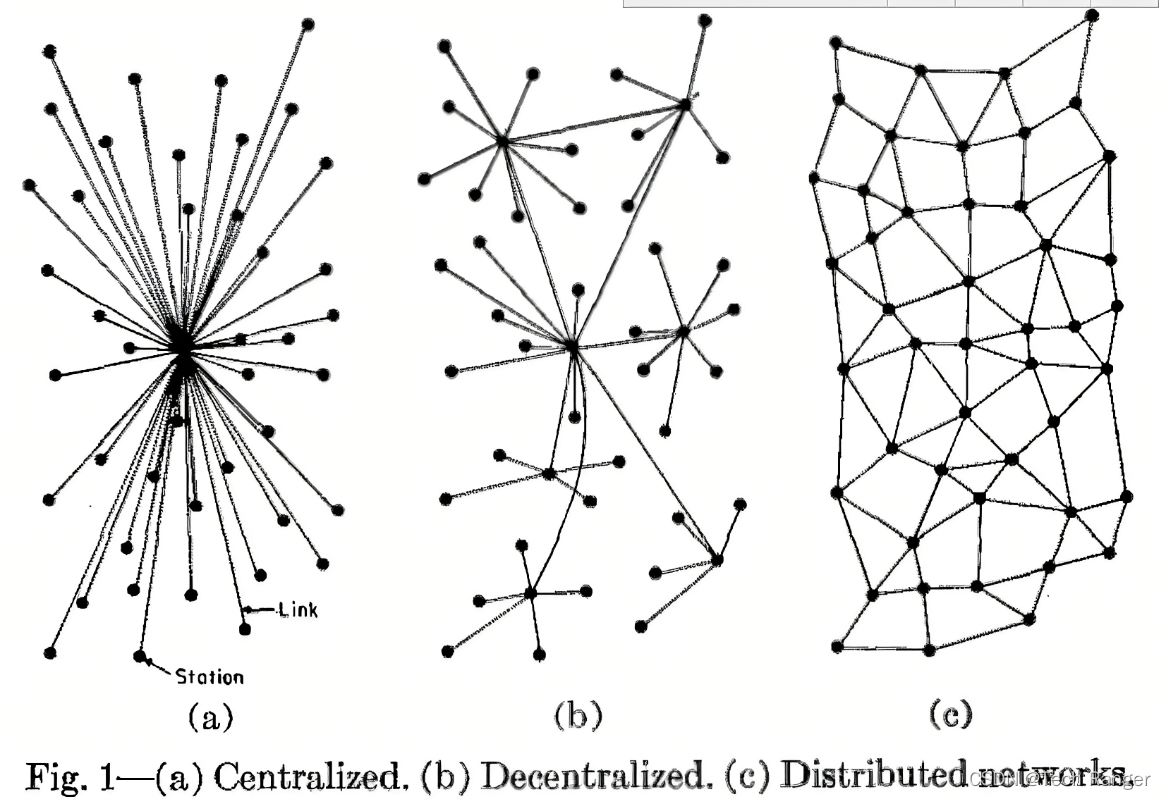
图 ( c ) 就是描述了一个去中心化的场景，比特币就是应用了这种技术，每两个人之间的交易会通知所有网络中的用户。
示例：
用户 A 支付用户 B 5个比特币，同时网络中的用户 C 和 D 也会收到消息，

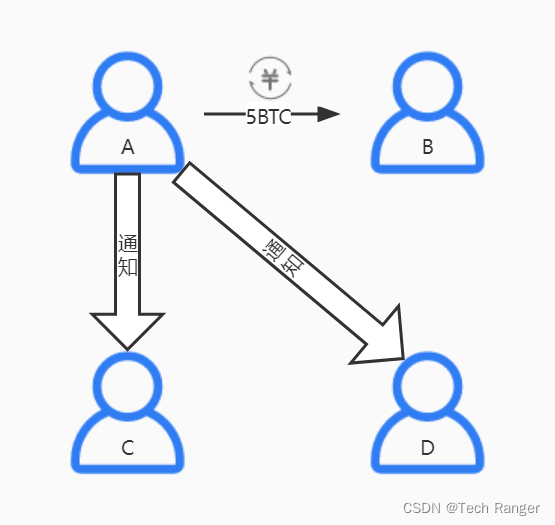
几条交易信息的账单打包形成一个区块(Block)，区块大小约为 1M ，每个区块保存大约4000条信息。每个区块连接在一起形成一条区块链(BlockChain)。

设计好这样一个系统后，还存在以下几个问题：
①账单的基准
网络中不同用户获取交易信息的顺序不同，导致每个用户得到的账单不同。
②记账的原因
记账的设计原理，比特币支付系统需要记账的原因。
③账单的防伪
保证系统中的交易信息是准确的、确定发生的、不会被篡改的。

1.3 记账的原因——激励机制(Incentive)

①手续费
如果一个交易的输出值小于其输入值，那么这个差值就是交易的手续费，手续费被附加到包含这个交易的区块的奖励中。

The incentive can also be funded with transaction fees. If the output value of a transaction is less than its input value, the difference is a transaction fee that is added to the incentive value of the block containing the transaction. Once a predetermined number of coins have entered circulation, the incentive can transition entirely to transaction fees and be completely inflation free

②打包奖励
这一段说出了比特币的来源，即一个块的第一个交易是一个特殊交易，这个块的创造者被凭空赋予一定数量的比特币。
在系统创造的初期，中本聪规定比特币总数有 2100 万个，每产生 21000 个区块，比特币奖励的数量减半，每 10 分钟产生一个区块，到 2140 年所有比特币耗尽。

By convention, the first transaction in a block is a special transaction that starts a new coin owned by the creator of the block. This adds an incentive for nodes to support the network, and provides a way to initially distribute coins into circulation, since there is no central authority to issue them.
The steady addition of a constant of amount of new coins is analogous to gold miners expending resources to add gold to circulation. In our case, it is CPU time and electricity that is expended.

1.4 账单的基准——工作量证明(Proof-of-Work, PoW)

每个网络中的参与者都希望获取打包奖励，而同时由于整个网络是去中心化的，因此每一个节点在获取到一定的交易信息后都可以打包区块，且每一个区块都不相同，那么以哪一个账单作为基准，哪一个节点可以获取打包奖励，这时引入了工作量证明机制，通过用枚举的方式暴力计算一个复杂的哈希值，来抢夺记录区块的权力，这个抢夺记账权的过程就被称作挖矿。

To implement a distributed timestamp server on a peer-to peer basis, we will need to use a proofof-work system similar to Adam Back’s Hashcash [6], rather than newspaper or Usenet posts.
The proof-of-work involves scanning for a value that when hashed, such as with SHA-256, the
hash begins with a number of zero bits. The average work required is exponential in the number
of zero bits required and can be verified by executing a single hash.

2 挖矿原理

2.1 哈希函数

通俗地理解哈希函数

定义： 哈希函数（英语：Hash function）又称散列算法、散列函数，是一种从任何一种数据中创建小的数字“指纹”的方法。散列函数把消息或数据压缩成摘要，使得数据量变小，将数据的格式固定下来。该函数将数据打乱混合，重新创建一个叫做散列值（hash values，hash codes，hash sums，或hashes）的指纹。散列值通常用一个短的随机字母和数字组成的字符串来代表。
简单讲就是
哈希函数（散列函数）能够将任意长度的输入值转变成固定长度的值输出，该值称为散列值，输出值通常为字母与数字组合。
SHA256算法： 对于任意长度的消息，SHA256都会产生一个256位的哈希值，称作消息摘要。
一文读懂SHA256算法原理及其实现
在比特币中使用的算法是SHA256算法，这个算法是由美国国家安全局开发的加密算法。
具体形式举例：

SHA256(BlockChain) = 3a6fed5fc11392b3ee9f81caf017b48640d7458766a8eb0382899a605b41f2b9

这个算法的特点是：正向运算简单，反向运算困难。

2.2 原理

①假设存在一个区块链

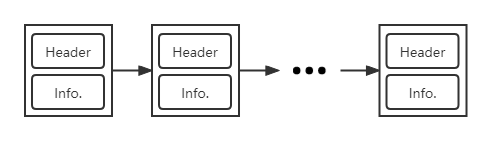
区块链上的每一个区块包含头部以及交易信息。
②此时几个用户准备好账单准备打包接块。

存在一个字符串 String 包含以下内容：
前块头部(Prev Hash)+账单+时间戳(timestamp)+随机数(Nonce）

For our timestamp network, we implement the proof-of-work by incrementing a nonce in the block until a value is found that gives the block’s hash the required zero bits. Once the CPU effort has been expended to make it satisfy the proof-of-work, the block cannot be changed without redoing the work. As later blocks are chained after it, the work to change the block would include redoing all the blocks after it.

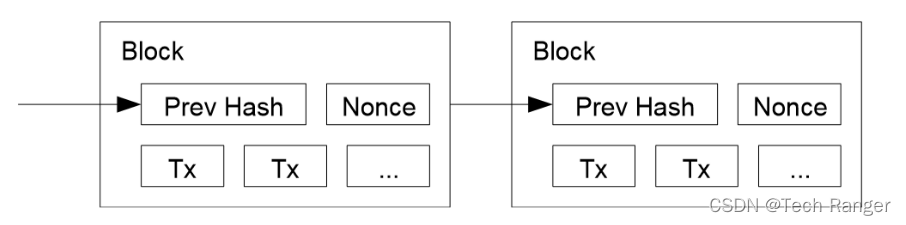
③对字符串 String 进行两次 SHA256 计算：

Hash = SHA256(SHA256(String))

运算后我们得到一个 256 位二进制数 b 。
④挖矿：
对上一步中得到的256位二进制数 b 做出规范，规定 b 的前 n 位都是 0 ，得出符合要求的哈希数就有资格打包。
通过不断修改枚举随机数(Nonce)，使得到的满足要求，这个过程就是挖矿的过程。

备注：每个人的前块头部都是相同的，但其他信息会有不同，因此算出这个哈希值的难度是不同的。

⑤打包：
将得到的哈希值作为头部和账单信息打包形成一个区块(Block)。

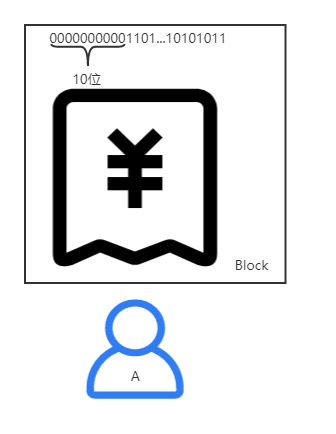
⑥获取打包奖励：
将得到的新块接到区块链后得到奖励。

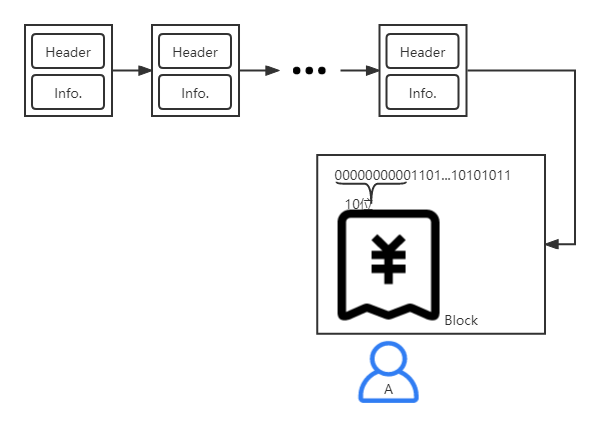
2.3 确定难度

哈希值中每一位出现 0 或 1 的概率都是 $\frac{1}{2}$，因此如果规定哈希值的前 n 位都是 0 概率为 $(\frac{1}{2}{)}^n$，所以 n 越大，正确得出所需哈希值的难度越大。
示例：
假设世界上存在 1万 台矿机，每台矿机的计算能力是 1T/s ，每秒钟可以计算 2 × 10${}^{12}$次
根据比特币系统的设计规则每10分中需要产生一个区块，因此当前所有矿机总的计算次数为
1 × 10${}^{12}$ × 10(min) × 60(sec) = 6 × 10${}^{14}$
经过计算
6 × 10${}^{14}$ ≈ $2^{49}$
因此，难度系数 n = 49

3 交易真实——签名认证

3.1 电子签名

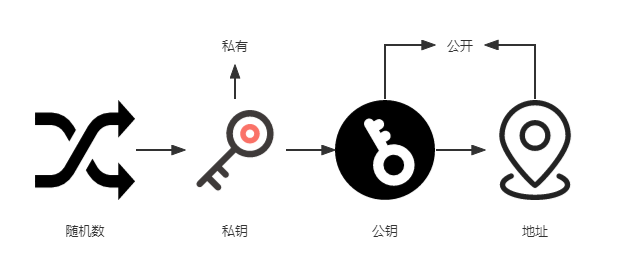
①比特币注册的过程中会生成一个随机数(random number)；
②通过系统产生的随机数产生一个私钥(private key)；
③私钥会再产生一个公钥(public key)字符串；
④再产生一个地址(address)。

3.2 非对称加密

非对称加密： 加密使用公钥，解密使用私钥，任何人都可以使用公钥加密。

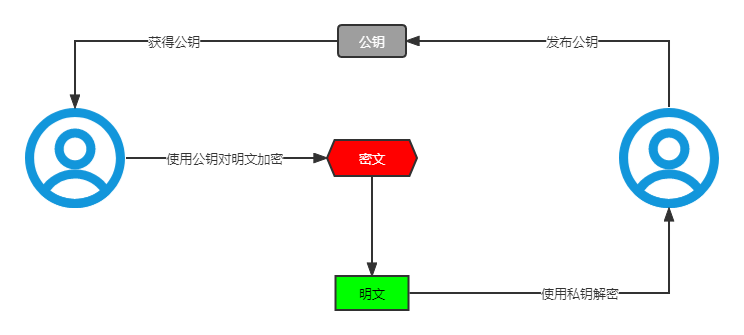
比特币使用了最流行的非对称加密算法——RSA加密算法。
RSA加密算法

RSA加密算法： 加密和解密数据围绕着模幂运算，这是取模计算中的一种。

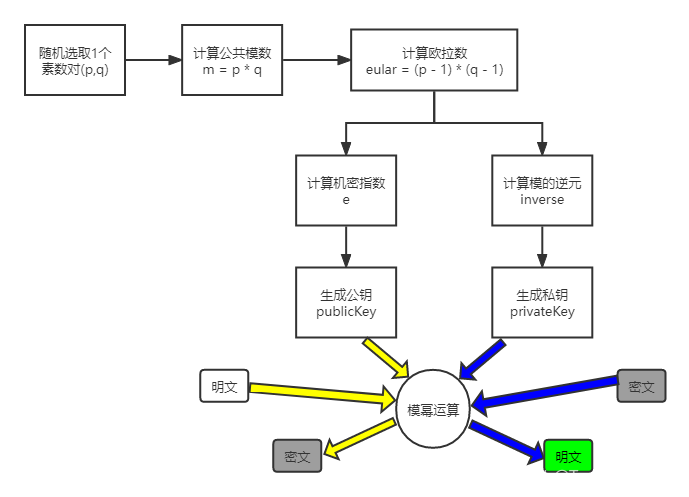
代码示例：

public class RSA {    
    /**
     * 获得(公/私)密钥
     */
    public final Map<String, RSAKey> getCipherKeys() {
        ...
        int[] primes = getRandomPrimes(2);
        int modulus = modulus(primes[0], primes[1]);
        int euler = euler(primes[0], primes[1]);
        int e = cipherExponent(euler);
        int inverse = inverse(euler, e);
        publicKey.setExponent(e);
        publicKey.setModulus(modulus);
        privateKey.setExponent(inverse);
        privateKey.setModulus(modulus);
        ...
    }
    
    /**
     * 加密
     */
    public int encode(int plaintext, RSAPublicKey key) {
        return modularPower2(plaintext, key.getExponent(), key.getModulus());
    }
    
    /**
     * 解密
     */
    public int decode(int chipertext, RSAPrivateKey key) {
        return modularPower2(chipertext, key.getExponent(), key.getModulus());
    }
 
    // 随机生成count个素数
    private final int[] getRandomPrimes(int count) {
        ...
        try {
            primeLabels = FileReadUtils.readLines("./data/prime_table");
        } catch (IOException e) {
            e.printStackTrace();
        }
        for (int i = 0; i < primes.length; i++) {
            primes[i] = Integer.parseInt(primeLabels.get(indexs.get(i)));
        }
 
        return primes;
    }
 
    // 计算公共模数
    private final int modulus(int p, int q) {
        return p * q;
    }
 
    // 计算欧拉数
    private final int euler(int p, int q) {
        return (p - 1) * (q - 1);
    }
 
    // 计算加密指数
    private final int cipherExponent(int euler) {
        Random random = new Random();
 
        int e = 7;
        do {
            e = random.nextInt(euler - 1);
        } while (!isCoprime(e, euler) || e <= 1);
 
        return e;
    }
 
    // 判断两个数互素
    private final boolean isCoprime(int number1, int number2) {
 
        int sqrt = (int) Math.sqrt(Math.max(number1, number2));
        for (int i = 2; i <= sqrt; i++) {
            if (number1 % i == 0 && number2 % 2 == 0) {
                return false;
            }
        }
 
        return true;
    }
 
    // 计算“模的逆元”
    // (d * e) ≡ 1 mod euler
    private final int inverse(int euler, int e) {
        ...
        while (flag) {
            q = m[2] / n[2];
            for (int i = 0; i < 3; i++) {
                temp[i] = m[i] - q * n[i];
                m[i] = n[i];
                n[i] = temp[i];
            }
            if (n[2] == 1) {
                if (n[1] < 0) {
                    n[1] = n[1] + euler;
                }
                return n[1];
            }
            if (n[2] == 0) {
                flag = false;
            }
        }
        return 0;
    }
    
    // 模幂运算
    private final int modularPower(int base, int e, int modular) {
        int result = 1;
        do {
            if (isOdd(e)) {
                result = (result * (base % modular)) % modular;
                e -= 1;
            } else {
                base = (base * base) % modular;
                e /= 2;
            }
        } while (e > 0);
        
        result %= modular;
        
        return result;
    }
}

3.3 比特币支付流程

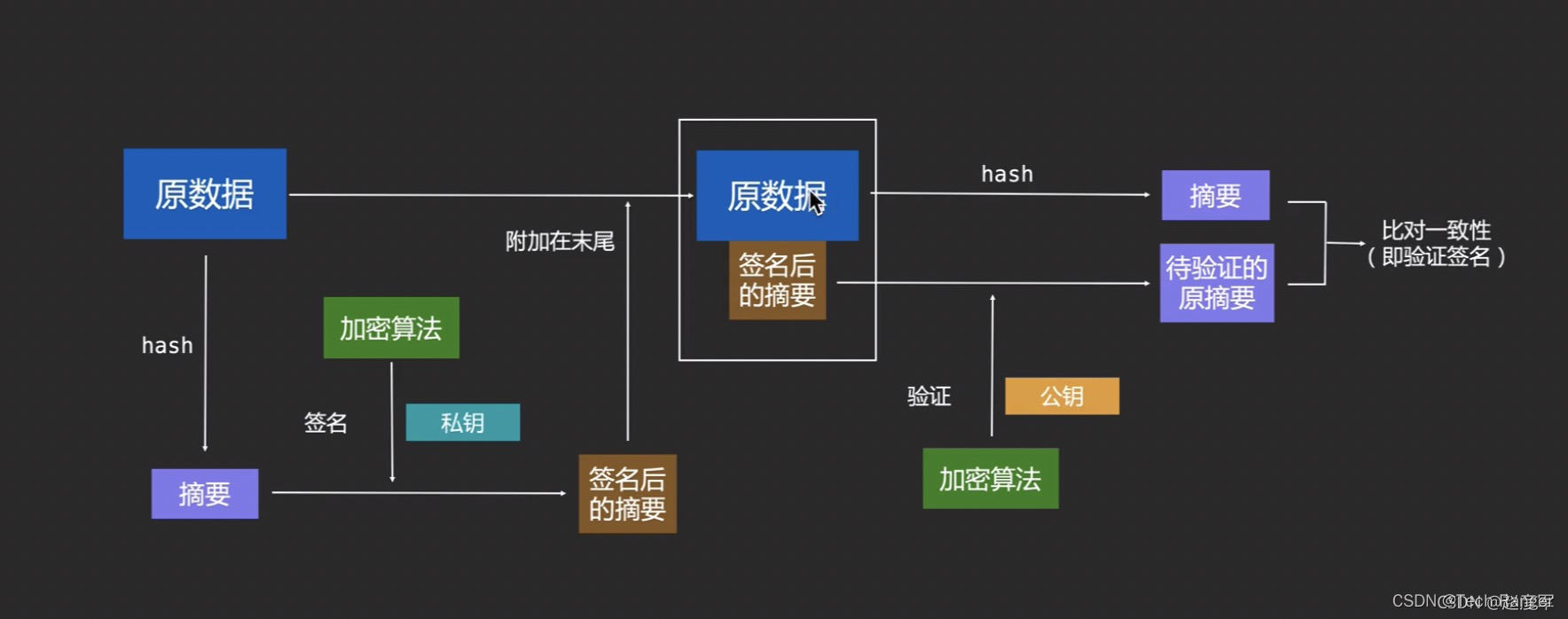
①用户A支付用户B，5个比特币，用户A记录这一转账信息；
②用户A将这条信息进行数字摘要处理，即SHA256运算；
③将得到的摘要，通过私钥对摘要进行加密，得到密码；
④将记账信息、公钥、密码向网络中进行广播；
⑤收到广播的人，先对A的记账信息进行Hash运算得到摘要，再公钥对密码进行解密得到待验证的摘要，将两个摘要进行对比，两者相同相同证明该消息真实。

4　双重支付

4.1 余额检查

每个系统中的用户都知道所有区块中的交易信息，在信息确认过程中，会检查区块中的交易信息，确认发起支付的用户有足够的余额完成支付。
示例：
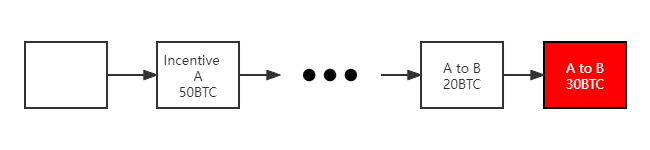
假设存在以下一条区块链，此时经过检查用户 A 还有余额 30 个比特币，如果此时 A 支付给 B 30 BTC，可确认该交易真实，如果此时 A 支付给 B 40 BTC，A 没有足够的余额，该交易不成立。

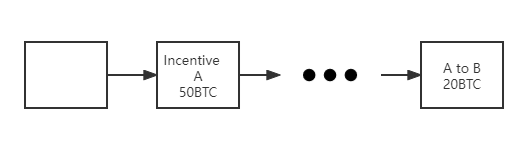
当交易信息存在新的区块里，此时该交易信息得到确认。

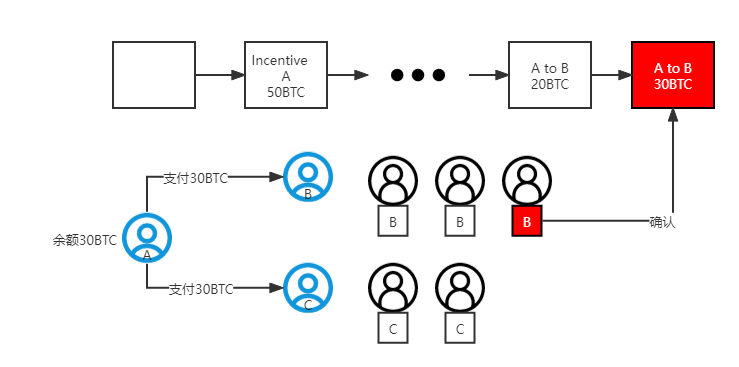
4.2 双重支付

①假设用户 A 同时向用户 B 和用户 C 支付30个比特币；
②由于网络的延迟等原因，网络中的不同用户会收到两条中的一条消息，当接收到其中一条后，会检查 A 的余额，自动拒绝另一条消息；
③每个用户将自己接收到的消息打包到自己的区块里；
④当有一个用户解决了哈希运算难题，将自己打包的区块接到区块链上，此时这条信息得到确认，其他收到另一条信息的人自动选择得到确认的信息。

4.3 防止篡改

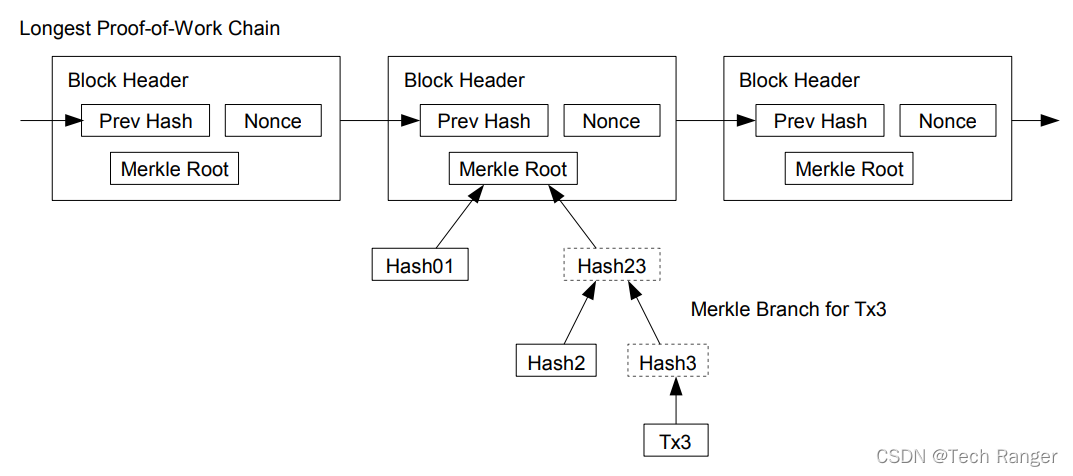
①最长连原则(Longest Proof-of-Work Chain)
当有两个区块同时接在区块链上，这样区块链形成两个分支，不同分支上的矿工继续以自己为准各自挖矿，当有一个分支上的矿工得到一个新的区块，那么此时他所在的分支就会延长，网络中的所有矿工就会以更长的分支为准。

It is possible to verify payments without running a full network node. A user only needs to keep a copy of the block headers of the longest proof-of-work chain, which he can get by querying network nodes until he’s convinced he has the longest chain, and obtain the Merkle branch linking the transaction to the block it’s timestamped in. He can’t check the transaction for himself, but by linking it to a place in the chain, he can see that a network node has accepted it, and blocks added after it further confirm the network has accepted it

②防伪
如果存在一个算力超强的矿工，在某一区块上形成一个新的分支并且疯狂挖矿超过当前的区块链的长度，那么理论上区块链是可以被篡改的。

As such, the verification is reliable as long as honest nodes control the network, but is more vulnerable if the network is overpowered by an attacker. While network nodes can verify transactions for themselves, the simplified method can be fooled by an attacker’s fabricated transactions for as long as the attacker can continue to overpower the network. One strategy to protect against this would be to accept alerts from network nodes when they detect an invalid block, prompting the user’s software to download the full block and alerted transactions to confirm the inconsistency. Businesses that receive frequent payments will probably still want to run their own nodes for more independent security and quicker verification.