开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 区块链 -> NJUPT 《信安数基》第 8 章证明题攻略 -> 正文阅读

[区块链]NJUPT 《信安数基》第 8 章证明题攻略

NJUPT 《信安数基》群论证明题攻略

注：本文章适合学习信息安全数学基础的同学们考前突击，不适用于数学系专业的同学。里面有些内容可能对于数学系来说是不严谨的，但对于信息安全专业为了应付考试的同学来说是完全够用的。

近世代数部分很多同学不会做的根本原因就在于基本性的概念没有搞懂，而信息安全数学基础这门课来说，它不会像数学系一样考特别难的证明（工科主要还是应用为主），因此复习的重点就在于了解所有的概念。~~而不是去背题~~。

这篇文章完全是自己总结的，主要是梳理一下概念性的东西、总结一些证明题的解题方法，构建完整的证明思路，考虑到网上资源较少，自己寒假又闲得无聊，那就写个造福一下学弟学妹们。

先放个图片镇楼。然后步入正题

在这里插入图片描述

1 群

1.1 群的概念

什么是群？课本P233讲得特别乱。简而言之就是：群是一个具有**封闭性、可结合、有幺元、任意元素可逆的一个代数系统。 **因此根据定义，我们可以很容易地得到群的性质：

群的性质：在群 $< G, ? >$ 中，有：

1.封闭性：即 $\forall a,b \in G$ ，都有 $ab\in G$ 。

2.结合性：即 $\forall a,b,c \in G$ ，都有 $a (b c) = (a b) c$ 成立

3.有幺元：即群中有一个元素 $e$ ，使得 $\forall a \in G$ ，都有 $a e = e a = a$ 成立。

4.任意元素可逆：即 $\forall a \in G$ ， $\exists b \in G$ ，使得 $a b = b a = e$ 成立。此时 $b$ 称为 $a$ 的逆元，记作 $a^{-1}$

群中的运算不一定具有交换性，有交换性的话，那么这个群是交换群。

所以如果我们要证明某个代数系统 $< G, ? >$ 是群，那么我们就用定义法证明，就像写八股文一样。

例题1：证明 $<\Z,+>$ 是群。其中 $\Z$ 是整数集合， $+$ 是普通加法。

①：由于 $\forall a,b \in \Z$ ，都有 $\in \Z$ 恒成立。故运算的封闭性成立

②：由于 $\forall a,b,c \in \Z$ ，都有 $(a + b) + c = a + (b + c)$ 成立。因此该运算具有结合性。

③：由于 $\forall a \in \Z$ ，都有 $a + 0 = 0 + a = a$ ，因此该运算具有幺元 $0$ 。

④：由于 $\forall a \in \Z$ ，都有 $\in \Z$ ，使得 $a + (? a) = (? a) + a = 0$ 成立。因此该集合中任意元素都具有加法逆元。

综上，由①②③④可知， $<\Z,+>$ 是一个群。

~~是不是很简单？~~。当然如果题目要求证明 $<\Z,+>$ 是一个交换群，那就加一步证明交换性就行了。（请读者尝试证明一下，只需要在上面证明群的步骤的基础上加个第五步对交换性的叙述就行。）

这里运算是加法，因此加法幺元是 $0$ ， $a$ 的加法逆元是 $? a$ 。

1.2 子群

由于群是一种代数系统，代数系统是由集合和集合上定义的运算组成的。因此子群的概念也很好理解了

如果 $< G, ? >$ 是一个群， $H\subseteq G$ ， $< H, ? >$ 也是一个群，那么 $< H, ? >$ 是 $< G, ? >$ 的子群，记作 $H \leq G$ 。其中 $?$ 运算是同一运算。

证明子群也可以用定义证明。

例题2：证明 $<5\Z,+>$ 是群 $<\Z,+>$ 的子群。其中 $5\Z=\text{\{}5k|k\in \Z \text{\}}$

①：由于 $\forall a,b \in 5\Z$ ，即 $a, b$ 都是 $5$ 的倍数，很显然 $a + b$ 还是 $5$ 的倍数。故运算的封闭性成立

②：由于 $\forall a,b,c \in 5\Z$ ，都有 $(a + b) + c = a + (b + c)$ 成立。因此该运算具有结合性。

③：由于 $\forall a \in 5\Z$ ，都有 $a + 0 = 0 + a = a$ ，因此该运算具有幺元 $0$ 。

④：由于 $\forall a \in 5\Z$ ，都有 $\in 5\Z$ ，使得 $a + (? a) = (? a) + a = 0$ 成立。因此该集合中任意元素都具有加法逆元。

很显然，对于任意整数 $a$ ， $5 a$ 还是整数。因此 $5\Z \subset \Z$ 。

所以 $<5\Z,+>$ 是 $<\Z,+>$ 的子群。

是不是几乎一模一样的操作？

当然，判断子群还有一个定理：

定理：设 $\subseteq G$ ， $< G, ? >$ 是群。若 $\forall a,b \in H$ ， $ab^{-1}\in H$ 恒成立。那么 $< H, ? >$ 是 $< G, ? >$ 的子群。

这样上面那个题我们还能这么证：

由于 $<\Z,+>$ 是群，设 $a,b\in 5\Z$ ，即 $a, b$ 都是 $5$ 的倍数。

又因为 $b$ 的加法逆元是 $? b$ ，由于 $b$ 是 $5$ 的倍数，那么 $? b$ 也是 $5$ 的倍数， $a + (? b)$ 也是 $5$ 的倍数。

所以 $\in 5\Z$ ，故 $<5\Z,+>$ 是 $<\Z,+>$ 的子群。

~~有没有顿时觉得似乎证明还是很简单的？~~，证明群就是写八股文，四个性质一凑就行！当然，在已知 $G$ 是一个群的情况下，我们也要学会利用这四个性质。

我们再来看两个题巩固一下：

例题3：设 $G$ 是一个群，且 $\forall a\in G$ ，都有 $a^{2}=e$ 成立，证明 $G$ 是交换群。

设 $a,b \in G $，由群的封闭性，可知 $ab\in G,ba\in G$ 。

所以我们可以得到 $a^{2}=b^{2}=(ab)^{2}=e$ ，即 $ab)^{2}=a^{2}b^{2}$ 。（注意： $ab)^{2}=(ab)(ab)=abab$ ，一般群不具有交换性）

展开平方，可得 $a b a b = a a b b$ ，两边左乘一个 $a$ ，右乘一个 $b$ ，可以得到 $a^{2}(ba)b^{2}=a^{2}(ab)b^{2}$ 。

消去平方，有 $b a = a b$ 成立，所以 $G$ 是一个交换群。

我们再上一点难度（这个题建议模仿上面的方法，自己做一下再看答案）

例题4：在群 $G$ 中， $\forall a,b$ ，都有 $a^{3}b^{3}=(ab)^{3},a^{4}b^4=(ab)^4,a^5b^5=(ab)^{5}$ ，证明 $G$ 是一个交换群。

因为 $a^{3}b^{3}=(ab)^{3}$ ，所以 $a(ab)^{3}b=a(a^3b^3)b=a^{4}b^{4}=(ab)^{4}=a(ba)^{3}b$ 。即 $a(ab)^{3}b=a(ba)^{3}b$ 。等号两边左乘 $a^{-1}$ ，右乘 $b^{-1}$ ，可得到 $ab)^{3}=(ba)^{3}$ （P.S.由于 $G$ 是群，因此 $a^{-1}$ 可以直接写）

又因为 $a^{4}b^{4}=(ab)^{4}$ ，所以 $a(ab)^{4}b=a(a^4b^4)b=a^{5}b^{5}=(ab)^{5}=a(ba)^{4}b$ 。即 $a(ab)^{4}b=a(ba)^{4}b$ 。等号两边左乘 $a^{-1}$ ，右乘 $b^{-1}$ ，可得到 $ab)^{4}=(ba)^{4}$ 。（这一步可以直接同理可知）。

两边同时右乘 $ab)^{3}$ 的逆元（即 $ab)^{-3}$ ），得到 $ab)^{4}(ab)^{-3}=(ba)^{4}(ab)^{-3}$ ，即 $ab)^{4}(ab)^{-3}=(ba)^{4}(ba)^{-3}$ ，也就是 $a b = b a$ ，故群 $G$ 是交换群。

这边还要提醒一下，这边的次方是对同一个运算连续多次的简写，不一定是乘法。比如在加法群 $<\R,+>$ 中， $4^{3}$ 表示三个 $4$ 相加，因此结果是 $12$ 。但在乘法群 $R-{0},×>$ 中， $4^{3}$ 才表示三个 $4$ 相乘，结果是 $64$ 。

2 正规子群和商群

2.1 简单理解陪集、商集、正规子群、商群

8.2节，课本上讲得可谓是令人一头雾水。。。。先看一下课本上是怎么对陪集下定义的：

类似于模同余的分类，人们可以通过 $G$ 的子群 $H$ 对群 $G$ 进行分类
$aH=\{c|c\in G,c^{-1}a\in H\}$

所以我们来大概说一下陪集是什么。陪集就是一堆集合。 $ 5\Z$ 是 $\Z$ 的子群，运算法则是加法。那么我们就可以导出 $\Z$ 上 $5\Z$ 的陪集有。
$5\Z,1+5\Z,2+5\Z,3+5\Z,4+5\Z$
其中 $1+5\Z=\{...,-4,1,6,11,...\}$ ， $2+5\Z=\{...,-3,2,7,12,...\}$ ，以此类推。确实，跟同余扯上了一些关系。。。

上面 $5$ 个集合中，只有 $5\Z$ 上的加法构成群，其他集合上的加法都不构成群！！！（因为不满足封闭性）

然后商集就是所有陪集构成的集合，其本质是集合的集合。 $\Z/5\Z$ 的结果就是把上一行全部加上大括号。。
$Z/5\Z=\{5\Z,1+5\Z,2+5\Z,3+5\Z,4+5\Z\}$
下面自己请尝试写出 $\R/\Z$ 的结果（答案：$ {a+\Z|a\in[0,1) }$）。

然后我们会发现： $\Z/5\Z$ 也是一个集合（它里面有 $5$ 个元素，每个元素是模 $5$ 的同余类）。如果我们定义运算 $\bigoplus_5 $ 为模 $5$ 加法，那么可以证明： $<\Z/5\Z,\bigoplus_5 >$ 是一个群。换句话说， $\Z/5\Z$ 也构成了一个群。

由于我们一开始得出，当运算为加法时， $\Z$ 是群， $5\Z$ 也是群，并且商集 $\Z/5\Z$ 也可以构成群。那么我们可以有这样两个结论：

因为商集 $\Z/5\Z$ 可以构成群，所以

① $5\Z$ 是 $\Z$ 的正规子群

② $\Z/5\Z$ 是一个 $\Z$ 上的一个商群

这边要说明一下： $\Z/5\Z$ 跟 $Z_5$ 是不一样的概念，因为 $Z_5 =\{0,1,2,3,4\}$ ，而 $Z/5\Z=\{5\Z,5\Z+1,5\Z+2,5\Z+3,5\Z+4\}$ 。前者中的元素是数字，后者中的元素是集合。

2.2 相关证明方法

1. 证明两个陪集相等

陪集的性质： $H$ 是 $G$ 上的子集， $a,b\in G$ 。那么有：

① $aH=bH\Leftrightarrow b^{-1}a\in H$

② $aH\cap bH=\phi \Leftrightarrow b^{-1}a \not \in H$ 。

③ 任意两个陪集要么相等，要么不交。也就是 $aH \cap bH=\phi$ 或 $a H = b H$ ，没有其他的关系

举个例子： $4+5\Z=9+5\Z$ ，因为 $-9+4=-5\in 5\Z$ 。而 $4+5\Z \not=3+5\Z$ ，因为$-3+4=1 \not \in 5\Z $。

2. 证明某个子群 $H$ 是群 $G$ 的正规子群

正规子群的证明方法：

设 $a\in G$ ， $H$ 是 $G$ 的子群，如果我们想证明 $H$ 是 $G$ 的正规子群，只需要证明
$aHa^{-1} \subset H$

当然还有一个性质，读者可以尝试证明，这个结论最好别直接用，因为一部头就能出来

若 $G$ 是交换群， $H$ 是 $G$ 的子群，则 $H$ 一定是 $G$ 的正规子群

下面我们来看一个例子：

例题5：设 $G$ 是一个群， $C=\{a|a\in G,\forall b\in G \rightarrow ab=ba\}$ 。证明 $C$ 是 $G$ 的正规子群。

先证明 $C$ 是 $G$ 的子群：

①：由于 $G$ 是一个群，故 $G$ 上有幺元 $e$ ，且 $\forall g\in G$ 都有 $g e = e g = g$ ，所以 $e\in C$ 。 $C$ 上有幺元 $e$ 。

②：由于 $G$ 是一个群，故 $G$ 中的运算具有结合性， $C$ 是 $G$ 的子集，故该运算的结合性在 $C$ 中仍成立

③：设 $\in C,g\in G$ 那么 $(s t) g = s (t g) = s (g t) = (s g) t = g s t = g (s t)$ ，说明 $st\in C$ ，可知该运算在 $C$ 上也具有封闭性。

（注：这里 $s t g = s g t$ 是利用的 $C$ 上元素的性质，看看 $C$ 中元素是怎样定义的，既然 $t\in C,g\in G$ ，那么 $t g = g t$ 是成立的，随意换括号是因为 $G$ 是群， $G$ 上的结合性成立）

④：设 $s\in C,g\in G$ ，由 $s g = g s$ ，则 $s^{-1}(sg)s^{-1}=s^{-1}(gs) s^{-1}$ ，也就是 $gs^{-1}=s^{-1}g$ （请自己去括号看看），可知 $s^{-1} \in C$ 。

由①②③④可知， $C$ 是一个群，且 $C$ 是 $G$ 的子群。下面证明 $C$ 是 $G$ 的正规子群

设 $g\in G,s\in C$ ，则有 $gsg^{-1} = (gs)g^{-1} =(sg)g^{-1}=s$ ，说明 $gsg^{-1} \in C$ ，即 $gCg^{-1} \subset C$ 。可知 $C$ 是 $G$ 的正规子群。

在上面这个题中，你会发现证明 $C$ 是 $G$ 的子群仍然是用定义，四步法证明的。而证明 $C$ 是 $G$ 的正规子群，用的就是定义法证明的。所以定义还是最重要的。

3 同态和同构

3.1 定义

书上对于同态和同构的定义是这么说的：

设 $f$ 是群 $G$ 到群 $G^{'}$ 的映射/函数，若 $\forall a,b\in G$ ，都有 $f (a) f (b) = f (a b)$ 恒成立，则 $f$ 是 $G$ 到 $G^{'}$ 的同态。

特殊地，若 $f$ 是单射就是单同态， $f$ 是满射就是满同态。若 $f$ 既是单同态又是满同态，则 $f$ 是同构。

P.S：单射就是一对一的映射，用符号语言就是：若 $f(x_1)=f(x_2)$ ，则一定有 $x_1=x_2$ 。满射就是映射/函数的值域充满整个 $G^{'}$ 集合，即对于任意的 $\in G'$ ，总存在 $x\in G$ ，使得 $y = f (x)$ 成立。

举个例子：设 $f$ 是 $\R$ 到 $\R$ 的映射，则 $f(x)=e^{x}$ 是单射但不是满射， $f(x)=x\sin x$ 是满射但不是单射， $f(x)=x^{3}$ 既是单射又是满射， $f(x)=\sin x$ 既不是单射又不是满射。

3.2 证明方法

所以我们得到了同态和同构的证明方法（依旧是定义法）：

证明同态的方法：找一个从 $G$ 到 $G^{'}$ 的函数 $f$ ，证明对于 $G$ 中任意的 $a, b$ ，都有 $f (a b) = f (a) f (b)$ 成立。

证明同构的方法：找一个从 $G$ 到 $G^{'}$ 的函数 $f$ ，证明这个函数具有：①同态性，②单射，③满射。固定的三个步骤，就像证明群有固定的四个步骤一样。

当然，还有几个性质需要了解一下，可以直接用：

若 $f$ 是群同态，则一定有 $f (e) = e^{'}$ ， $f(a^{k})=[f(a)]^{k}$ 都是成立的。

单射的充要条件： $ker f=\{e\}$ 。满射的充要条件： $f (G) = G^{'}$

还有几个概念需要了解一下：

同态核 $\mathrm{ker} f=\{x|x\in G 且 f(x)=e'\}$ （ $e^{'}$ 是群 $G^{'}$ 的幺元）。例如：从 $<\Z,+>$ 到 $<\Z_{5},\bigoplus_5 >$ 上的映射 $f(x)=x\mod 5$ 。很显然， $f(a)\bigoplus_5 f(b)=f(a+b)$ 是成立的。所以这是一个同态。而 $Z_5$ 中的幺元是 $0$ ，因此我们想要有 $0 = f (x)$ ，那么我们可以得到 $x\in 5\Z=\{5k|k\in Z\}$ 。所以在这边， $\mathrm{ker}f=5\Z$ 。

请注意这边的 $Z_{5}$ 和 $5\Z$ 的区别（上面已经提到），以及 $\Z$ 上运算和 $Z_{5}$ 上运算的不同之处，上面 $a, b$ 是 $\Z$ 中元素， $f (a), f (b)$ 是 $Z_{5}$ 中元素。

同态基本定理：若 $f$ 是 $G$ 到 $G^{'}$ 的满同态，则 $G/\mathrm{ker}f$ 与 $G^{'}$ 同构

例题6：证明同态基本定理

设 $F$ 是 $G/\mathrm{ker}f$ 到 $G^{'}$ 的映射， $F(a\ker f)=f(a)$

①：证明 $F$ 是同态：因为 $f$ 是同态，所以 $f (a b) = f (a) f (b)$ ，所以 $F(a\ker f)F(b\ker f)=F(ab\ker f)$ 成立，故 $F$ 是同态。

②：证明 $F$ 是单射：若 $a\ker F \in \ker F$ ，那么有 $F(a\ker f)=f(a)=e'$ 。所以 $a\in \ker f$ ，故 $a\ker f=\ker f$ 。因此我们有 $ker F =\{\ker f\}$ 。 $\ker F$ 中只有一个元素，故 $F$ 是单射。

③：由于 $f$ 是满同态，故对于任意 $y\in G'$ ，总存在 $x\in G$ 使得 $y = f (x)$ 。这样我们就有 $F(x\ker f)=y$ 成立，故 $F$ 是满射。

由①②③可知： $F$ 是满射，故 $G/\mathrm{ker}f$ 与 $G^{'}$ 同构。

值得注意的是： $G/\ker f$ 是集合的集合，所以 $F$ 的定义域是 $G/\ker f$ 中的元素（该元素的类型是集合），值域是 $G^{'}$ 中的元素。

我们再来看一个证明同构的例子

例题7：设 $G$ 是一个群， $a\in G$ ， $f(x)=axa^{-1}$ 。证明 $f$ 是 $G$ 到 $G$ 的自同构。

①：证明同态：设 $s,t\in G$ ，则 $f(s)f(t)=asa^{-1}ata^{-1}=as(aa^{-1})ta^{-1}=asta^{-1}=f(st)$ ，所以 $f$ 具有同态性。

②：证明单射：设 $f(x_1)=f(x_2)$ ，即 $ax_1a^{-1}=ax_2a^{-1}$ ，两边左乘一个 $a^{-1}$ ，右乘一个 $a$ ，可以得到 $a^{-1}ax_1a^{-1}a=a^{-1}ax_2a^{-1}a$ ，即 $x_1=x_2$ 成立。故 $f$ 是单射。

③：证明满射：设 $y=f(x)=axa^{-1}$ ，则 $a^{-1}ya=x$ ，即 $y=f(a^{-1}ya)$ ，故 $f$ 是满射。

由于群中的运算具有封闭性，故由①②③可知， $f$ 是 $G$ 到 $G^{'}$ 的自同构。

~~所以证明同构依旧是写八股文。~~直接用定义法一把梭。

4.循环群

4.1 几个定义

设 $G$ 是一个群

$G$ 中元素 $a$ 的阶 $\mathrm{ord}(a)$ ：使 $a^{k}=e$ 的最小正整数 $k$ ，且 $k$ 一定是 $∣ G ∣$ 的因数

若 $G$ 中存在一个元素 $g$ ，使 $G=\{g,g^2,g^3,...\}$ ，则 $G$ 是循环群， $g$ 是 $G$ 的生成元。（类比模素数原根）

循环群的性质：

循环群一定是交换群

无限阶循环群与 $<\Z,+>$ 同构，有限阶（ $n$ 阶）循环群与 $<\Z_n,\bigoplus_n>$ 同构。

若 $g$ 是群 $G$ 的生成元，若 $∣ G ∣ = + \infty$ ，则 $G$ 只有两个生成元 $g$ 和 $g^{-1}$ 。若 $∣ G ∣ = n$ ， $g^{k}|_{\gcd(k,n)=1}$ 是 $G$ 的生成元。

请读者自己尝试证明： $<\Z_{41}^*,\bigotimes_{41}>$ 与 $<\Z_{40},\bigoplus_{40}>$ 这两个群同构，其中 $\bigotimes_{41}$ 是模 $41$ 乘法， $\bigoplus_{40}$ 是模 $40$ 加法。

提示：模 $41$ 的一个原根是 $6$ 。

答案：设 $f$ 是 $Z_{40}$ 到 $Z_{41}^*$ 上的函数， $f(x)=6^{x} \mod {41}$

①：由于 $\varphi(41) = 40$ 。设 $a,b\in \Z_{40}$ 。故 $6^{a\bigoplus_{40}b}\mod 41=6^a\bigotimes_{41}6^b=f(a)\bigotimes_{41}f(b)$ ，故 $f$ 具有同态性。

②：若 $f(x_1)=f(x_2)$ ，即 $6^{x_1}\equiv 6^{x_2} \pmod{41}$ 。所以 $x_1\equiv x_2 \pmod {40}$ 。又因为 $x_1,x_2 \in \Z_{40}$ ，故只有 $x_1=x_2$ 成立，故 $f$ 是单射。

③：由于 $6$ 是模 $41$ 的原根，故模 $41$ 的一个完全剩余系可写为 ${6,6^{2},6^{3},...,6^{40}=6^0=1\}$ ，即 $6^{i},i\in \Z_{40}$ 遍历了模 $41$ 的完全剩余系，故 $f$ 是满射。

由①②③可知， $<\Z_{41}^*,\bigotimes_{41}>$ 与 $<\Z_{40},\bigoplus_{40}>$ 这两个群同构

4.2 证明方法

证明某个群是循环群，就是要找到它的生成元，若为有限循环群（阶为 $n$ ），找出一个阶为 $n$ 的元素即可。

例7：证明素数阶群一定是循环群

设 $∣ G ∣ = p$ 是素数，则对于群 $G$ 中的任意元素，阶只有可能是 $1$ 或 $p$ 。

设 $\not = e$ ，则 $a$ 的阶不可能是 $1$ ，故只有 $a$ 的阶是 $p$ 。所以 $a$ 是群 $G $ 的生成元， $G$ 是循环群

例8：已知群 $G$ ， $∣ G ∣ = p q$ ，其中 $p, q$ 是不同的素数，证明 $G$ 是循环群。

证明：由于 $∣ G ∣ = p q$ ， $p, q$ 是不同的素数，故对于任意元素 $a$ ， $a$ 的阶只有可能是 $1, p, q, p q$ 四种情况。若 $a\not =e$ ，则 $a$ 的阶只能是 $p, q, p q$ 。

设 $g,h\in G$ ， $\mathrm{ord}(g)=p,\mathrm{ord}(h)=q$ 。由于群 $G$ 中运算的封闭性，故 $gh\in G$ 。

则有 $(gh)^{1}\not =e$ ， $(gh)^{p}=g^ph^p=h^p\not =e$ ， $(gh)^{q}=g^qh^q\not =e$ ，说明 $(g h)$ 的阶不可能是 $1, p, q$ 。

故 $\mathrm{ord}(gh)=pq=|G|$ 。 $g h$ 是 $G$ 的生成元，故群 $G$ 是循环群。

是不是感觉脑子有点乱了？那我就上大招了！。

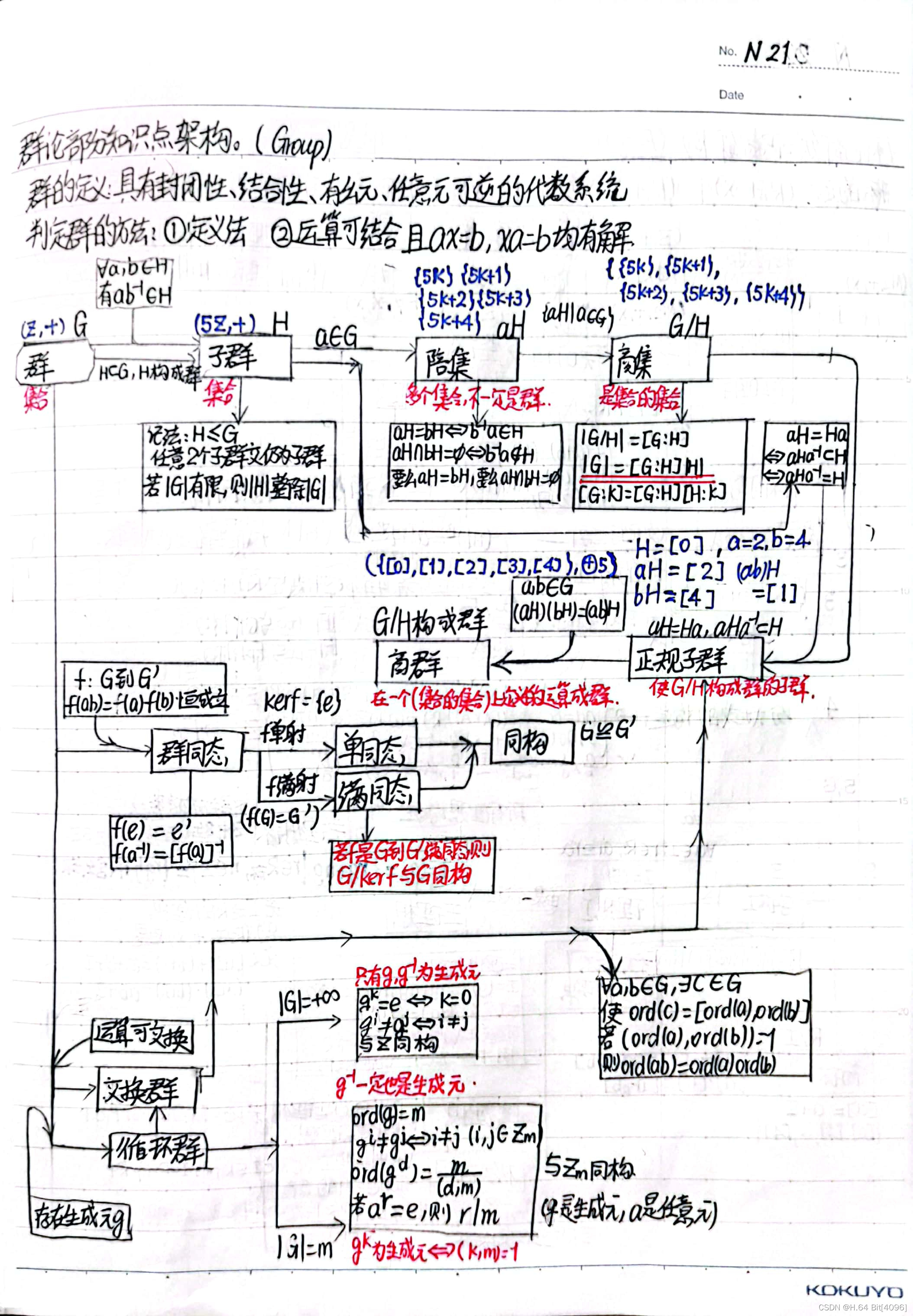
5 群论部分证明题思路汇总

$a$ 的阶只能是 $p, q, p q$ 。

设 $g,h\in G$ ， $\mathrm{ord}(g)=p,\mathrm{ord}(h)=q$ 。由于群 $G$ 中运算的封闭性，故 $gh\in G$ 。

则有 $(gh)^{1}\not =e$ ， $(gh)^{p}=g^ph^p=h^p\not =e$ ， $(gh)^{q}=g^qh^q\not =e$ ，说明 $(g h)$ 的阶不可能是 $1, p, q$ 。

故 $\mathrm{ord}(gh)=pq=|G|$ 。 $g h$ 是 $G$ 的生成元，故群 $G$ 是循环群。