[区块链]基于同态加密的隐私计算技术在基因序列演化分析场景的应用

一、概述

数据要素的流通共享和核心价值挖掘是数据要素市场培育的核心内容、必须在保证隐私安全的前提下实现有效信息共享。然而，当前仍然有三大隐私制约数据流通与协作。一是“数据孤岛”现象普遍存在，“数据孤岛”的出现使数据共享和流通协作受到阻碍，导致数据要素在资产化过程中发生垄断；二是全球数据合规监管日趋严格，日前各个国家都才采取数据安全法，确立了数据安全保护的各项基本制度，导致企事业及个人对数据流通与协作合法合规的担忧；三是隐私泄露事件频发导致信任鸿沟，各个应用软件为了商业变现对个人隐私的侵犯无处不在，导致我们越来越不信任软件的各种安全验证。

近年来，全球新冠肺炎确诊病例逾千万，且仍以每天30万新增病例飙升，一些发展中国家 正在成为新“震中”，形势堪忧。新冠病毒毒性大，隐密性、变异性强，扩散快，稍有松懈便可酿成大患，对新型冠状病毒基因组演化的分析能够为全面评估疫情风险、启动公共卫生应对措施及制定医疗方案提供有效的数据支撑。本文使用基于同态加密的隐私计算技术对新冠病毒基因序列演化进行分析，使在不泄露原始数据的前提下，采取多方不同机构的病毒数据源对基因序列进行综合分析,进而达到快速定位新变种基因的种族归簇问题。

二、相关工作

隐私计算是在保证数据提供方不泄露敏感数据的前提下，对数据进行计算并能验证计算结果的技术。在大数据时代能够打破数据孤岛，既能保护数据隐私安全、防止敏感信息泄露的同时又能实现海量数据流动。隐私计算经过近几十年的发展、目前在产业互联网、人工只能、金融科技、医疗保护共享数据等方面发挥着重要的作用。而现有的隐私保护主要从信息处理过程、隐私度量与评估两个方面入手，其技术主要分为访问控制技术、信息混淆技术方法、密码学技术方法，但是以上方案主要是针对特征场景局部数据集的具体算法，缺少针对各种场景的普适性算法框架。

隐私计算的提出解决了上述问题，隐私计算可分为联邦学习（Federated Learning，FL）、同态加密（Homomorphic Encryption,HE）、多方安全计算（Secure Multi-Party Computation，SMPC)、基于可信计算（Trust Execution Environment，TEE）、差分隐私（Differential Privacy，DP）等技术。

可信执行环境（Trust Execution Environment，TEE）通过硬件技术来对数据进行隔离保护，将数据分类处理。支持TEE的CPU中，会有一个特定的区域，该区域的作用是给数据和代码的执行提供一个更安全的空间，并保证它们的机密性和完整性。典型场景包联合建模、区块链、intel的SGX等

联邦学习（Federated Learning，FL）是近些年新崛起的新兴人工智能技术，在2016年由谷歌最先提出，保证数据不出安全控制范围，保护终端数据和个人数据隐私的前提下，实现多个参与方或多个计算节点之间开展高效率的机器学习。联邦学习的典型场景有金融联合风控、联合营销、联合画像等。

安全多方计算（Secure Multi-Party Computation，SMPC)解决的是一组相互不信任的参与方各自拥有秘密数据，协同计算一个既定函数的问题。参与方除了获得计算结果，无法获得之外的任何信息。在整个计算过程中，参与方拥有对自身数据的绝对控制权。安全多方计算的典型场景有数据安全查询，联合统计分析、拍卖、薪酬统计、联合建模等。

差分隐私（Differential Privacy，DP）具备严谨的数据理论，其本质是对计算结果的保护而不是计算过程。差分隐私的优点在于具备和背景知识严格无关的隐私保护模型，理论上可以抵御任何攻击。差分隐私当前实现的主要方式是在结果集中添加噪音，解决单个查询的隐私保护问题。

同态加密（Homomorphic Encryption,HE）是一种特殊的加密算法，在密文基础上直接进行计算，与基于解密后的明文是一样的计算结果。同态加密是基于非对称密码算法，公钥是公开的，参与方使用公钥进行加密，只有私钥持有者才能解密最终结果。同态加密分为半同态加密PHE（Partially/Semi?Homomorphic Encryption）,基本同态加密SHE（Somewhat?Homomorphic Encryption）、全同态加密FHE（Fully?Homomorphic Encryption）如图1所示同态加密算法的发展历程。

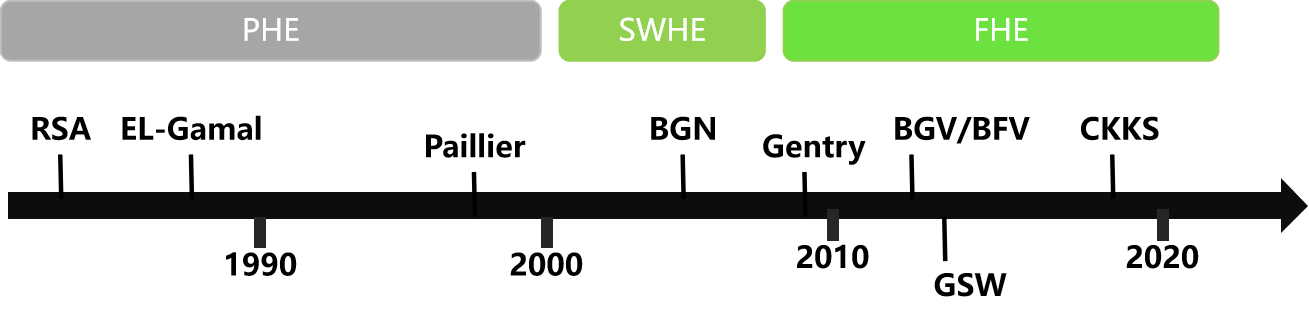
图1.同态加密算法研发历程

其中半同态加密PHE是指只能支持明文空间内部分某一类型代数运算的同态密文运算，例如乘法同态(RSA、EL-Gamal)公式2-1,加法同态(Paillier)公式2-2

基本同态指支持明文空间内定义的所有运算,比如加法和乘法的同态运算。但支持的运算的次数有限。例如Boneh-Goh-Nissim(BGN)公式2-3仅支持一次乘法同态运算。

全同态指支持明文空间内定义的所有运算的任意深度，不限制次数的同态密文运算。虽然BGV、BFV、CKKS等属于全同态加密算法，但是他们限制乘法的深度，属于分层全同态加密算法。

目前、全同态加密算法仍处于学术研究为主的发展阶段，但是最为主流的同态加密方案是整数型加密算法BFV和浮点型加密算法CKKS。本文使用同态加密技术的全同态加密技术(CKKS)作为对基因数据的加密。

三、演化分析算法结构

本文使用全同态加密算法(CKKS)对数据进行加密实现在无可信第三方参与且数据安全的情况下对新冠病毒基因的演化分析进行。如图1.所示基于同态加密的新冠病毒基因演化分析整体架构图。其中由请求方B向同态加密模块发起加密计算请求，同态加密模块使用CKKS算法生成上下文并分别发送给A、B两方。双方在各自本地通过上下文分别生成密文数据发送给密文计算模块。密文计算模块首先对密文数据先进行相似性计算构建(m+n)阶方阵(m:A方数据条数；n:B方数据条数)。然后根据相似性矩阵和基因编码数组构建距离矩阵,最后NJ树模块根据距离矩阵生成基因关系结构并生成可视化文件返回给加密请求方B。

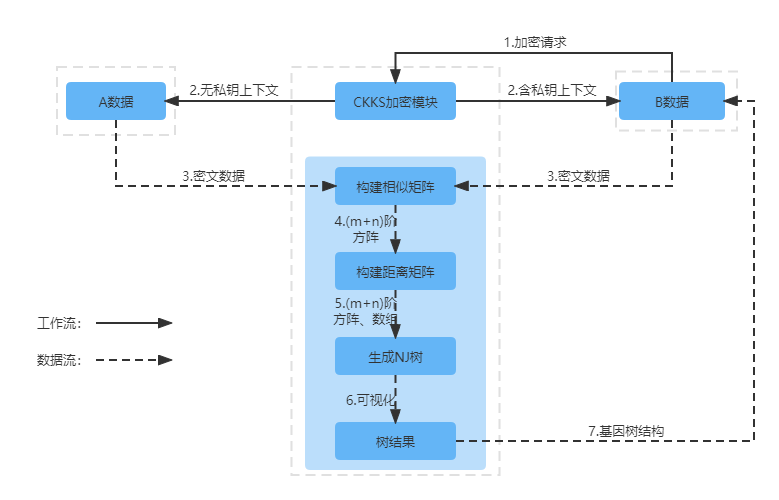
图1.基于同态加密的新冠病毒基因演化分析整体架构图

3.1、CKKS全同态加密流程

新冠病毒基因演化分析采用CKKS全同态加密算法。CKKS同态加密是把实数域中的数或者向量映射到多项式域（加密），在多项式域里做一些多项式加法和多项式乘法的运算之后，再把多项式映射回实数域（解密），得到的结果和实数域里做对应的加法和乘法的结果相同或者相似的一种加密计算技术。如图2.CKKS全同态加密技术基本流程图，总结下来，整体构建过程如下：

1. 使用encoder 将 数据data编码为明文Plaintext

2. 使用encrypt 将 明文Plaintext加密为密文Ciphertext

3. 使用Encrypted computation对密文Ciphertext 运算为 密文Ciphertext’

4. 使用decrypt 将 密文Ciphertext’解密为明文Plaintext’

5. 使用decoder 将明文Plaintext’解码为数据data’

CKKS原理介绍请阅读论文《Homomorphic Encryption for Arithmetic of Approximate Numbers》或参考CKKS同态加密算法简介进行学习。

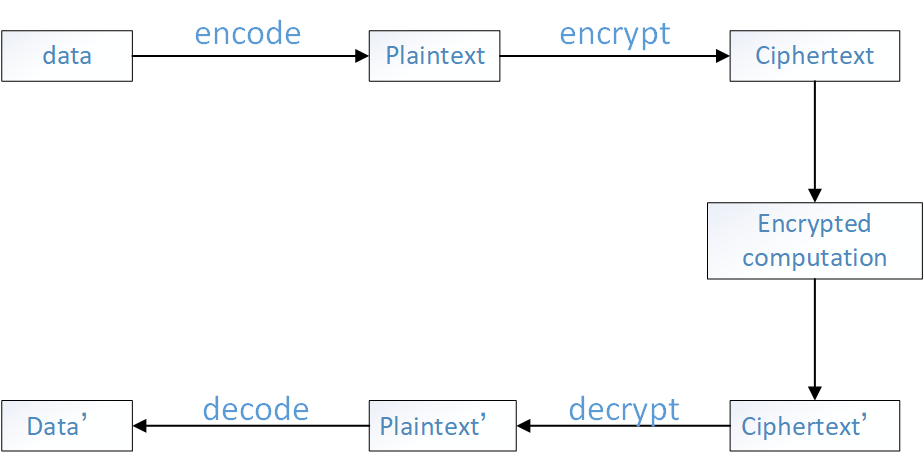
如图2.CKKS全同态加密技术基本流程图

3.2、密文计算模块

新冠病毒基因数据在本地加密形成密文后，发送到密文计算模块。密文计算模块包括构建距离矩阵、构建相似矩阵、构建距离矩阵和构建 NJ树。最后对NJ算法的输出进行可视化展示树结构。

3.2.1、构建相似矩阵

本文采用更改后的欧式距离计算不同基因序列间的相似度，具体如公式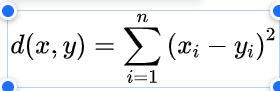(1)。

(1)

其中x，y分别为不同的基因，i为密文向量中的对应位置。

相关代码如下：

#定义0加密变量
a1=[0]
encrypted_vector0 = ts.ckks_vector(context,a1)
#定义无穷大加密变量
wuqong=[99999999999999999999999999999]
encrypted_vector_wuqiong = ts.ckks_vector(context,wuqong)

# 欧式距离公式
def eucliDist(a1, a2):
    return a1.sub(a2).square().sum()

# 构建相似矩阵
def align_star_multiple(sswq,seqLength,genLength):
    scores = np.empty((seqLength, seqLength), dtype=object)
    pairs = list(itertools.combinations(list(np.arange(len(Sseq))), 2))
    for x in range(seqLength):
        scores[x][x]=encrypted_vector0
        for y in range(x):# 时间缩小一倍
            if x != y:
                #scores[x, y] = MSE(Sseq[0],Sseq[1],genLength) 
                scores[x, y]=scores[y,x] = eucliDist(Sseq[x], Sseq[y])
    return scores

3.2.2、构建距离矩阵

构建距离矩阵的目的是使基因唯一标识和基因相似矩阵对应起来，为构建NJ树的NJ方法准备入参，需要对基因标识和基因近似结果进行封装。文章DissimilarityMatrix所用data变量用来保存2.2.1节计算出的相似矩阵，ids是存入基因唯一标识列表。详细代码见链接

3.2.3、构建NJ树

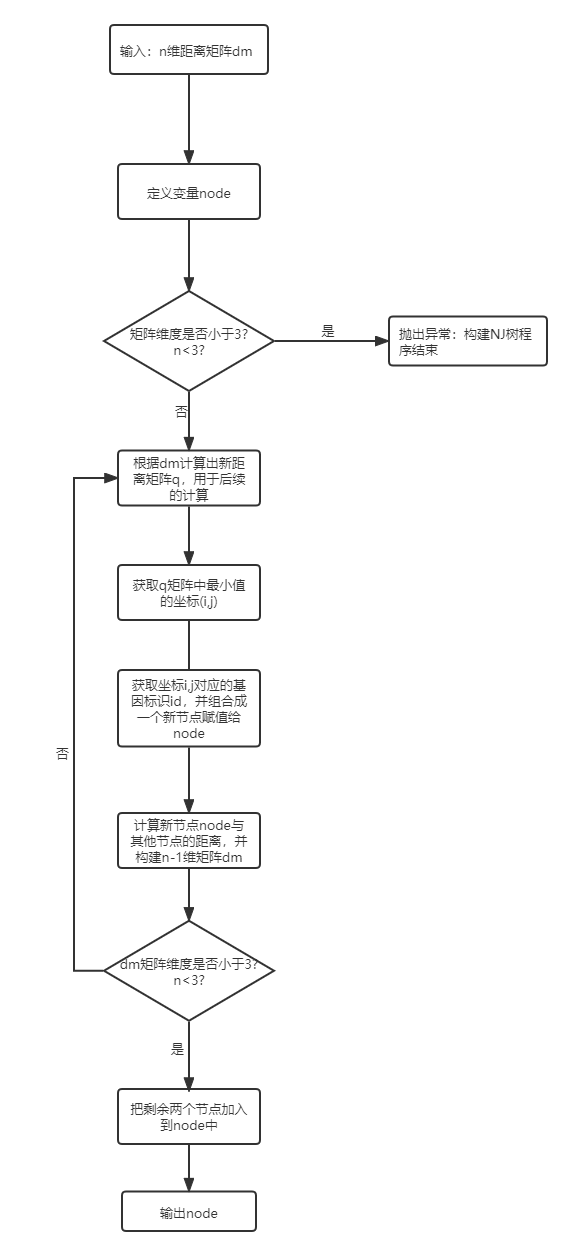
本文采用基于NJ算法构建NJ树结构，入参是n维距离矩阵，返回符合newick格式的基因编码关系字符串。因为一个基因和两个基因是无法构建NJ树结构，所以首先判断构建距离矩阵的基因数量是否小于3个。接着开始对距离矩阵中的每个基因逐个进行对比，先获取矩阵中最小值的下标。然后根据下标在基因标识数组中获取对应的基因编码。接着根据拿到的最小值下标(i,j)以及距离矩阵获取新的节点。最后生成新的n-1维的距离矩阵。循环遍历直到n小于3。最后输出整个newick格式的字符串。最后调用skibio包的treeNode方法进行可视化成树状关系结构。详细代码如下所示。相关流程如下图所示。

三、实验结果

本文使用基于同态加密的新冠病毒基因演化分析架构对200条新冠病毒基因进行结构化分析，部分分析结果截图如图3所示：

?相关代码请查看：https://download.csdn.net/download/dingyustefan/81879983

新冠病毒基因数据集：https://download.csdn.net/download/dingyustefan/81881954