[区块链]知道创宇区块链安全实验室｜浅谈 Curve - 稳定币兑换协议

简介

Curve 协议，一种基于以太坊平台的去中心化交易所，主要聚焦于稳定币、封装资产等的交易。相对于其他 DEX ，Curve 提供的交易对更集中，拥有极低的滑点和手续费，可以满足巨额的资产交易需求。极低的滑点和手续费以及 crv 的生态，都使得 Curve 在众多 DeFi 协议中能占据重要的一席之地。

StableSwap

StableSwap 是 Curve 在白皮书中设计提出的一种稳定币交易模型，该模型能提供极低的交易滑点和无限的流动性。

做市函数

StableSwap 模型的恒定函数做市商曲线（CFMM）如下：

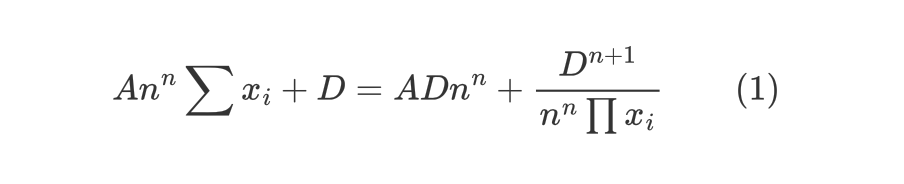
该设计理念基于融合恒定和与恒定积两种做市模型，兼具了恒定和的低滑点以及恒定积的无限流动性的特点

推导

假设现共有n个稳定币，则有：

给恒定和部分添上杠杆系数，并加上恒定积部分，则有：

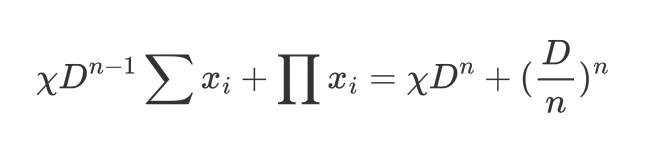
其中系数$\chi$引入了偏度的概念，由放大系数和偏度构成，其中偏度用来衡量流动池中各代币的平衡程度

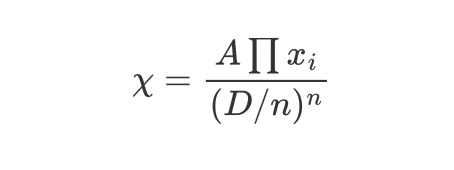
结合以上两式化简即可得出公式(1)

特点

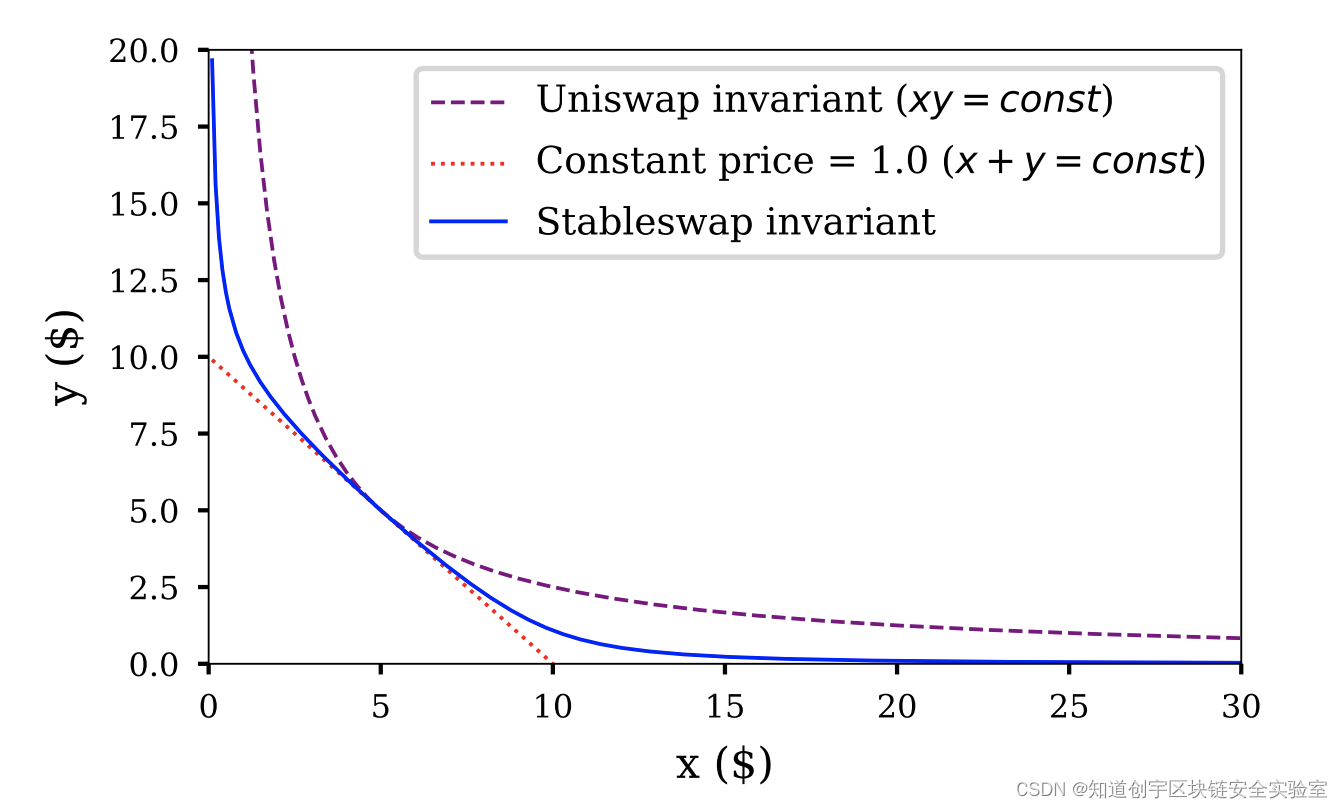
StableSwap 模型的曲线兼具恒定和与恒定积的特点，在各稳定币相对平衡的情况下，公式由恒定和占主导，曲线趋于直线，滑点较低；当在极端情况下，各稳定币不平衡，则公式由恒定积占主导，曲线与坐标轴无交点，不会出现流动性枯竭的情况

Basepool

basepool 为 Curve 推出的基础兑换池，最常见的有 3pool，由三种稳定币 DAI、USDC、USDT 组成

basepool 合约实现了基本的 StableSwap 交易模型

参数计算

StableSwap 模型的做市曲线公式(1)中，有两个重要的参数A与D，其中参数A为放大系数，由官方调整设置每个池子的放大系数；而参数D则为池中代币总量，是动态变化的。在 basepool 合约中，参数D的计算由_get_D函数实现：

@pure
@internal
def _get_D(_xp: uint256[N_COINS], _amp: uint256) -> uint256:
    """
    D invariant calculation in non-overflowing integer operations
    iteratively

    A * sum(x_i) * n**n + D = A * D * n**n + D**(n+1) / (n**n * prod(x_i))

    Converging solution:
    D[j+1] = (A * n**n * sum(x_i) - D[j]**(n+1) / (n**n prod(x_i))) / (A * n**n - 1)
    """
    S: uint256 = 0
    Dprev: uint256 = 0

    for _x in _xp:
        S += _x
    if S == 0:
        return 0

    D: uint256 = S
    Ann: uint256 = _amp * N_COINS
    for _i in range(255):
        D_P: uint256 = D
        for _x in _xp:
            D_P = D_P * D / (_x * N_COINS)  # If division by 0, this will be borked: only withdrawal will work. And that is good
        Dprev = D
        D = (Ann * S / A_PRECISION + D_P * N_COINS) * D / ((Ann - A_PRECISION) * D / A_PRECISION + (N_COINS + 1) * D_P)
        # Equality with the precision of 1
        if D > Dprev:
            if D - Dprev <= 1:
                return D
        else:
            if Dprev - D <= 1:
                return D
    # convergence typically occurs in 4 rounds or less, this should be unreachable!
    # if it does happen the pool is borked and LPs can withdraw via `remove_liquidity`
    raise

_get_D函数的算法将做市函数公式(1)以D为变量，通过牛顿迭代法计算出合适的D值，算法可谓精妙简洁

同样的算法还用于_get_y函数计算y值

@view
@internal
def _get_y(i: int128, j: int128, x: uint256, _xp: uint256[N_COINS]) -> uint256:
    """
    Calculate x[j] if one makes x[i] = x

    Done by solving quadratic equation iteratively.
    x_1**2 + x_1 * (sum' - (A*n**n - 1) * D / (A * n**n)) = D ** (n + 1) / (n ** (2 * n) * prod' * A)
    x_1**2 + b*x_1 = c

    x_1 = (x_1**2 + c) / (2*x_1 + b)
    """
    # x in the input is converted to the same price/precision

    assert i != j       # dev: same coin
    assert j >= 0       # dev: j below zero
    assert j < N_COINS  # dev: j above N_COINS

    # should be unreachable, but good for safety
    assert i >= 0
    assert i < N_COINS

    A: uint256 = self._A()
    D: uint256 = self._get_D(_xp, A)
    Ann: uint256 = A * N_COINS
    c: uint256 = D
    S: uint256 = 0
    _x: uint256 = 0
    y_prev: uint256 = 0

    for _i in range(N_COINS):
        if _i == i:
            _x = x
        elif _i != j:
            _x = _xp[_i]
        else:
            continue
        S += _x
        c = c * D / (_x * N_COINS)
    c = c * D * A_PRECISION / (Ann * N_COINS)
    b: uint256 = S + D * A_PRECISION / Ann  # - D
    y: uint256 = D
    for _i in range(255):
        y_prev = y
        y = (y*y + c) / (2 * y + b - D)
        # Equality with the precision of 1
        if y > y_prev:
            if y - y_prev <= 1:
                return y
        else:
            if y_prev - y <= 1:
                return y
    raise

流动性

Curve 池的流动性添加不同于 Uniswap 必须添加交易对的两种资产，basepool 可以仅添加池中某一种资产

@external
@nonreentrant('lock')
def add_liquidity(_amounts: uint256[N_COINS], _min_mint_amount: uint256) -> uint256:
    """
    @notice Deposit coins into the pool
    @param _amounts List of amounts of coins to deposit
    @param _min_mint_amount Minimum amount of LP tokens to mint from the deposit
    @return Amount of LP tokens received by depositing
    """
    assert not self.is_killed  # dev: is killed

    amp: uint256 = self._A()
    old_balances: uint256[N_COINS] = self.balances

    # Initial invariant
    D0: uint256 = self._get_D_mem(old_balances, amp) #hunya# 初始状态D0

    lp_token: address = self.lp_token
    token_supply: uint256 = CurveToken(lp_token).totalSupply()
    new_balances: uint256[N_COINS] = old_balances
    for i in range(N_COINS):
        if token_supply == 0:
            assert _amounts[i] > 0  # dev: initial deposit requires all coins
        # balances store amounts of c-tokens
        new_balances[i] += _amounts[i]

    # Invariant after change
    D1: uint256 = self._get_D_mem(new_balances, amp) #hunya# 添加流动性后理论D1
    assert D1 > D0

    # We need to recalculate the invariant accounting for fees
    # to calculate fair user's share
    D2: uint256 = D1
    fees: uint256[N_COINS] = empty(uint256[N_COINS])
    mint_amount: uint256 = 0
    if token_supply > 0: #hunya# 非首次添加流动性进行手续费扣出
        # Only account for fees if we are not the first to deposit
        fee: uint256 = self.fee * N_COINS / (4 * (N_COINS - 1))
        admin_fee: uint256 = self.admin_fee
        for i in range(N_COINS):
            ideal_balance: uint256 = D1 * old_balances[i] / D0
            difference: uint256 = 0
            new_balance: uint256 = new_balances[i]
            if ideal_balance > new_balance:
                difference = ideal_balance - new_balance
            else:
                difference = new_balance - ideal_balance
            fees[i] = fee * difference / FEE_DENOMINATOR
            self.balances[i] = new_balance - (fees[i] * admin_fee / FEE_DENOMINATOR)
            new_balances[i] -= fees[i]
        D2 = self._get_D_mem(new_balances, amp) #hunya# 扣除手续费后的D2
        mint_amount = token_supply * (D2 - D0) / D0 #hunya# LP铸币量
    else:
        self.balances = new_balances
        mint_amount = D1  # Take the dust if there was any
    assert mint_amount >= _min_mint_amount, "Slippage screwed you"

    # Take coins from the sender
    for i in range(N_COINS):
        if _amounts[i] > 0:
            # "safeTransferFrom" which works for ERC20s which return bool or not
            _response: Bytes[32] = raw_call(
                self.coins[i],
                concat(
                    method_id("transferFrom(address,address,uint256)"),
                    convert(msg.sender, bytes32),
                    convert(self, bytes32),
                    convert(_amounts[i], bytes32),
                ),
                max_outsize=32,
            )
            if len(_response) > 0:
                assert convert(_response, bool)  # dev: failed transfer
            # end "safeTransferFrom"

    # Mint pool tokens
    CurveToken(lp_token).mint(msg.sender, mint_amount)

    log AddLiquidity(msg.sender, _amounts, fees, D1, token_supply + mint_amount)

    return mint_amount

Metapool

metapool 为 basepool 基础上扩展衍生的新池，用作将新型的稳定币向 basepool 的 LP 代币锚定。basepool 池的流动性提供者可以将 basepool 的 LP 代币再次在 metapool 中添加流动性，进一步赚取额外的交易手续费收益。

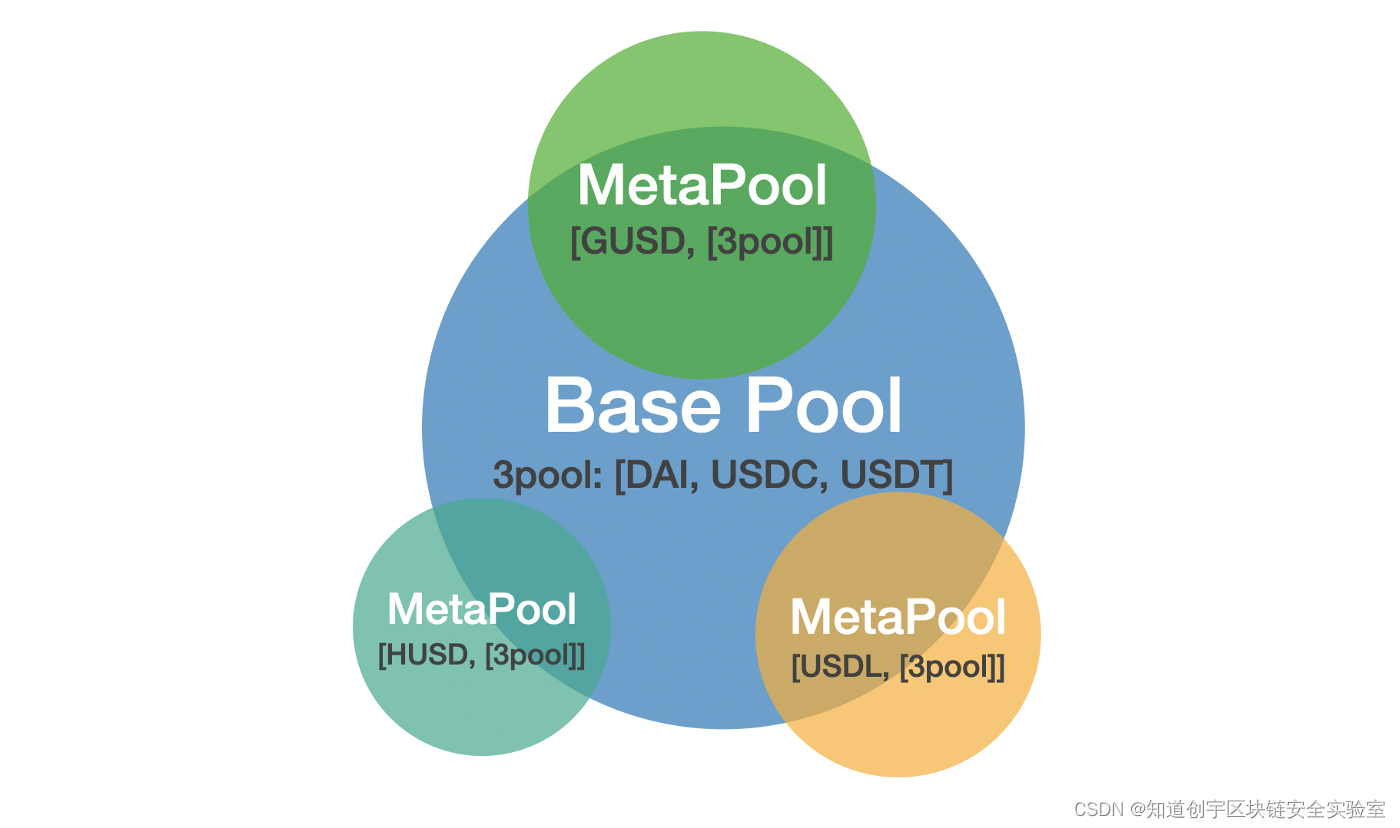
metapool 合约中，间接耦合了新型稳定币和基础池的稳定币，在提供了不同稳定币之间的兑换功能的同时，一定程度上分隔了新型稳定币的风险。

稳定币兑换

metapool 合约中的exchange_underlying函数实现了稳定币之间的相互兑换功能

@external
@nonreentrant('lock')
def exchange_underlying(i: int128, j: int128, _dx: uint256, _min_dy: uint256) -> uint256:
    ....
    # Use base_i or base_j if they are >= 0
    base_i: int128 = i - MAX_COIN
    base_j: int128 = j - MAX_COIN
    meta_i: int128 = MAX_COIN
    meta_j: int128 = MAX_COIN
    if base_i < 0:
        meta_i = i
    if base_j < 0:
        meta_j = j
    dy: uint256 = 0
    ...
    if base_i < 0 or base_j < 0: #hunya# 兑换中包含meta池代币
        old_balances: uint256[N_COINS] = self.balances
        xp: uint256[N_COINS] = self._xp_mem(rates[MAX_COIN], old_balances)

        x: uint256 = 0
        if base_i < 0: #hunya# 输入代币为meta池代币
            x = xp[i] + dx_w_fee * rates[i] / PRECISION
        else: #hunya# 输入代币为base池代币
            # i is from BasePool
            # At first, get the amount of pool tokens
            base_inputs: uint256[BASE_N_COINS] = empty(uint256[BASE_N_COINS])
            base_inputs[base_i] = dx_w_fee
            coin_i: address = self.coins[MAX_COIN]
            # Deposit and measure delta
            x = ERC20(coin_i).balanceOf(self)
            Curve(base_pool).add_liquidity(base_inputs, 0) #hunya# base池添加流动性
            # Need to convert pool token to "virtual" units using rates
            # dx is also different now
            dx_w_fee = ERC20(coin_i).balanceOf(self) - x
            x = dx_w_fee * rates[MAX_COIN] / PRECISION
            # Adding number of pool tokens
            x += xp[MAX_COIN]
        ...
        # Withdraw from the base pool if needed
        if base_j >= 0: #hunya# 输出代币为base池代币
            out_amount: uint256 = ERC20(output_coin).balanceOf(self)
            Curve(base_pool).remove_liquidity_one_coin(dy, base_j, 0) #hunya# base池移除流动性
            dy = ERC20(output_coin).balanceOf(self) - out_amount

        assert dy >= _min_dy, "Too few coins in result"

    else: #hunya# 纯base池代币兑换,直接调用base池exchange函数
        # If both are from the base pool
        dy = ERC20(output_coin).balanceOf(self)
        Curve(base_pool).exchange(base_i, base_j, dx_w_fee, _min_dy)
        dy = ERC20(output_coin).balanceOf(self) - dy
    ...

    log TokenExchangeUnderlying(msg.sender, i, _dx, j, dy)

    return dy

若兑换情况涉及 basepool 代币和 metapool 池代币，则会通过 basepool 的 LP 添加或移除流动性来做中间流程；若只是 basepool 代币的兑换，则直接调用 basepool 的exchange函数进行兑换。

总结

总的来看，无论是白皮书的理论设计还是代码的算法实现都是十分优秀的，理论设计巧妙夯实，代码算法高效简洁。这些优秀的实现都使得 Curve 在稳定对价资产交易领域中有着明显的竞争优势。