[区块链] 区块链可验证查询论文阅读（一）vChain: Enabling Verifiable Boolean Range Queriesover Blockchain Databases

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 区块链 -> 区块链可验证查询论文阅读（一）vChain: Enabling Verifiable Boolean Range Queriesover Blockchain Databases -> 正文阅读

[区块链]区块链可验证查询论文阅读（一）vChain: Enabling Verifiable Boolean Range Queriesover Blockchain Databases

2019年7月发表在顶会SIGMOD上的论文《vChain: Enabling Verifiable?Boolean?Range Queries over Blockchain Databases》，来自香港浸会大学。

1 论文解决的问题

如果想查询区块链中的数据，一种可行的做法是用户可以维护整个区块链数据库，并在本地查询数据。但是，通常区块链中所存储的数据量很大，下载完整的数据到本地需要很大的存储空间和网络带宽。另一种做法是，将完整数据存储在第三方服务提供者（Service Provider，SP），通过SP来进行查询，用户向SP发送查询请求指令，并等待接收从SP返回的结果。虽然这种做法省去了用户的本地存储和网络带宽的要求，但是SP不可信，所传回的查询结果可能是被篡改或者不完整的。用户的要求是收到的结果是健全的、完整的。

健全性是指结果返回的对象没有一个被篡改，且均符合查询条件；

完整性是指没有关于查询窗口或者订阅期的有效结果丢失。为了满足用户完整性、健全性的要求，论文提出了vChain框架，支持时间窗口查询，范围查询，Boolean查询（关键字查询），订阅查询。

论文的创新点：提出了一种基于累加器的验证数据结构ADS，该结构支持对任意查询属性进行动态聚合。进一步开发了两个新的索引来聚合块内和块间的数据记录，以实现高效的查询验证。同时还提出了倒置前缀树结构，加速大量订阅查询的处理。

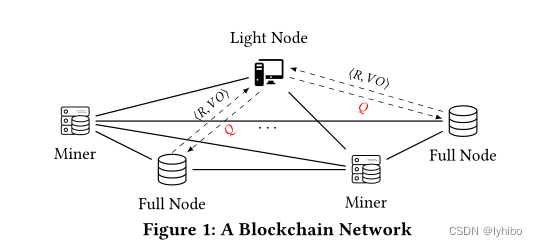
上图为区块链网络模型，其中有三种类型的节点，完整节点和矿工都作为全节点保存着区块链的完整数据集，区块头和区块体（数据记录），轻节点（用户）只保存区块链头部数据。轻节点可以通过向完整节点发送查询Q，完整节点向用户返回R和VO，R表示查询Q的结果，VO（verifiable object）是由SP构造的用于让轻节点验证查询结果的完整性和健全性的验证对象。

2 问题定义：

vChain系统模型：

数据对象表示形式：一个区块中存储多个数据对象，每一个对象被表示为<Ti, Vi, Wi>,其中i表示第i个对象，Ti表示对象的时间戳，Vi是多维度的矢量表示着一个或多个数字属性，Wi是一个集值属性。

时间窗口查询：一个查询的格式为q = ?[ts,te],[α,β],?? [公式] ,其中ts表示时间段的开始时间，te表示时间段的结尾时间，[α，β]是数字属性的多维范围选择谓词，?是一个在集值属性的单调布尔函数。所以用户可以通过时间窗口查询，或者使用数字范围查询或者使用某一个字段查询。SP返回这样的所有对象 {oi = ?ti,Vi,Wi? | ti∈ [ts,te]∧Vi∈[α,β]∧?(Wi) = 1}，假设?处于合取范式。

例如，q=?[2018-05, 2018-06], [10, +∞], send:1FFYc^receive:2DAAf?，以查找从2018年5月到6月发生的转账金额大于10并且与地址“send:1FFYc”和“receive:2DAAf”相关联的所有交易。

订阅查询：用户可以先提交查询，在未来如果区块链中有满足查询条件的数据，就向相应的订阅用户返回查询结果。订阅查询的形式是 q = ??,[α,β], ??，其中[α，β]和?与时间窗口查询的查询条件相同。SP连续返回所有对象，使得{ oi =?ti,vi,wi?| vi∈[α，β]∧?(wi） = 1 }直到查询被注销。
??比如，在基于区块链的汽车租赁系统中，每个租赁的客人的租赁价格存储了在Vi中和存储在Wi中的一组文本关键字。用户可以订阅查询q =? - ，[200,250]，“Sedan”∧（“Benz”∨“BMW”）?要收到在[200,250]范围内的价格的所有租赁消息并包含关键词“轿车”和“奔驰”或“宝马”。

论文用到的密码学知识：

哈希加密函数，双线性配对（Bilinear Pairing），多重集（Multiset），加密多重集累加器。

加密多重集累加器：多重集是允许元素出现多次的集合的概述。为了用常量大小表示它们，密码多集累加器是一个函数acc(·)，它以抗冲突的方式将一个多集映射到某个循环乘法群中的一个元素。
??累加器的一个有用性质是它可以用来证明集合不相交。它由以下概率多项式时间算法组成：
? KeyGen(1^λ) → (sk,pk): 在输入一个安全参数1^λ时，它生成一个秘钥sk和一个公钥pk。
? Setup(X,pk) → acc(X): 在输入多重集X和公钥pk时，它计算累积值acc(X)。
? ProveDisjoint(X1,X2,pk) → π：输入两个多重集X1, X2，其中X1∩X2=?，公钥pk，输出一个证明π。（SP证明查询不匹配时会用到）
? VerifyDisjoint(acc(X1),acc(X2),π,pk) → {0,1}: 输入累积值acc(X1)， acc(X2)，证明π，公钥pk，当且仅当X1∩X2=?时输出1。（用户验证用到）
?

3 基本解决方案

一个简单的方案是构造一个传统的MHT（默克尔哈希树）作为每个块的ADS，并应用传统的基于MHT的认证方法。但是这个传统的方法有3个主要的缺陷:

1)MHT仅支持构建默克尔树的查询键。为了支持涉及涉及任意属性集的查询，需要为每个块构造指数数量的MHT。

2)MHT不适用于集值属性。

3)不同块的MHT不能有效地聚合，使其无法利用块间优化技术。

为了克服这些缺点，提出了基于新的基于累加器的ADS方案的新型身份验证技术，该方案将数值属性转换为集值属性，并支持对任意查询属性进行动态聚合。

ADS生成和查询处理

?????论文为简单起见，仅考虑集值属性Wi的布尔查询条件。假设每个块存储一个对象oi= ?ti,Wi? ，然后用ObjectHash来表示原来的MerkleRoot。

ADS生成：在所提出的vchain框架中，在挖矿过程中为每个块生成ADS。它可以由SP使用，为每个查询构造验证对象（VO）。通过添加一个名为AttDigest的额外字段来扩展原始块结构，因此，区块头由PreBkHash, TS, ConsProof, ObjectHash, 和AttDigest组成。

想要作为ADS，Attdigest应该有三个性质：

1.AttDigest应该能够以某种方式总结一个对象的属性(Wi)这个可以用来证明对象是否匹配查询条件。如果是不匹配，可以返回这个digest而不是整个对象。

2.无论Wi中的元素数量如何，Attdigest都应该是恒定的大小。

3.（重要）AttDigest应该是可聚合的，以支持一个块内甚至跨块的多个对象的批量验证。因此，使用多重集累加器作为AttDigest:

它支持很多功能，包括显示不相交和验证不相交。

可验证的查询处理：给定一个布尔查询条件和一个数据对象，只有两种可能的结果:匹配或不匹配。第一种情况的正确性可以通过返回对象作为结果来容易地验证，因为它的完整性可以通过存储在区块头中的ObjectHash来验证，这对于轻节点上的查询用户是可做的。挑战在于如何使用AttDigest有效地验证不匹配的情况。由于 CNF 是用 OR 运算符的 AND 列表表示的布尔函数，我们可以将 CNF 中的布尔函数视为集合列表。

例如，一个查询条件“Sedan”∧(“Benz”∨“BMW”) 相当于两个集合 {“Sedan”} 和 {“Benz”,“BMW”}。考虑一个不匹配的对象： {“Van”,“Benz”}。很容易观察到存在一个等价集合(即{“Sedan”}) 使得它与对象属性的交集为空。

SP可以应用ProveDisjoint({“Van “，” Benz”}，{ " Sedan " }，pk) 生成一个不相交的证明π作为不匹配对象的VO(验证对象)。

相应地，用户可以从区块头中检索AttDigesti= acc({“Van”，“Benz”})，并使用VerifyDisjoint(AttDigesti，acc({“Sedan”})，π，pk)来验证不匹配。

范围查询的扩展

在许多情况下，用户还可能在数值属性Vi上应用范围条件。为了解决这一问题，提出了一种将数值属性转换为集值属性的方法。然后，范围查询可以相应地映射到布尔查询。

首先，用二进制格式表示每个数值。接下来，将一个数值转换为二进制前缀元素集合(用函数trans表示)。例如，数字4可以用二进制表示为100。因此，它可以转换成一个前缀集，比如trans(4) = {1?,10?,100}，其中?表示通配符匹配操作符。类似地，对于数值向量，可以对每个维度应用上述过程。例如，向量(4，2)具有二进制格式(100，010)。它转换的前缀集是{ $1*_{1}$ , $10*_{1}$ , $100*_{1}$ , $0*_{2}$ , $01*_{2}$ , $1*_{1}$ $010*_{2}$ }。这里每个元素都有一个下标符号（比如1,2）这是用于区分向量在不同维度中的二进制值。

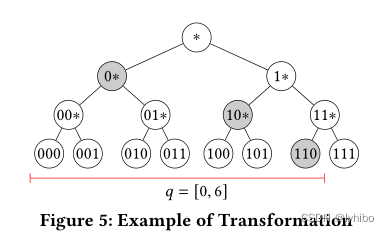
接下来，将范围查询条件转换为单调布尔函数，通过使用建立在整个二进制空间上的二叉树。上图示出了一维空间[0，7]的树。具体来说，对于一维范围[α，β]，首先以二进制格式表示α和β。接下来，将α和β视为树中的两个叶节点。最后，找到精确覆盖整个范围[α，β]的最小的树节点集。转换后的布尔函数是使用或(V)语义连接集合中每个元素的函数。

例如，对于一个查询范围[0，6]，我们可以找到它的转换布尔函数 0 ? ∨10 ? ∨110 （上图中灰色结点）。这个布尔函数的等价集是 {0?,10?,110}。类似地，在多维范围的情况下，转换后的布尔函数是一种使用AND (∧)语义连接每个维度的部分布尔函数。比如一个范围查询 [(0,3)，(6,4)] 可以转换成( $0*_{1}$ ∨ $10*_{1}$ ∨ $110*_{1}$ ) ∧ ( $011*_{2}$ ∨ $100*_{2}$ )相当于( $0*_{1}$ ， $10*_{1}$ ， $110*_{1}$ ) 和( $011*_{2}$ ， $100*_{2}$ )。

通过上述变换，关于数值Vi是否在范围[α，β]内的查询变成了对前缀集[α，β]的布尔查询。

比如查询 4 ∈ [0,6]，因为{1?,10?,100} ∩ {0?,10?,110} = {10?} != ?；

(4,2) 不属于[(0,3),(6,4)] 因为 {? $011*_{2}$ , $100*_{2}$ } ∩ { $1*_{1}$ , $10*_{1}$ , $100*_{1}$ , $0*_{2}$ , $01*_{2}$ , $010*_{2}$ } = ?。
通过上述数据转换技术，在接下来将这两种类型的查询条件统一为一个关于集值属性的统一布尔查询条件。更具体地，对于每个数据对象?ti,Vi,Wi?转换成元组?ti,W′i?，其中W’i=trans(Vi)+Wi；查询 q = ?[ts,te],[α,β],?? 转换成q=?[ts,te],?′?，其中 ?′= trans([α,β]) ∧ ?。所以查询结果为?{ Oi = ?ti,W′i? | ti ∈ [ts,te] ∧ ?′(W′i) = 1}。

它有一个缺点：只有整数才能被转化。

4 批量验证

批量验证可以加快认证速度。批量验证分为两类，一类是区块内部的批量认证，第二类是区块之间的。论文分别针对这两类设计了相应的索引（块内索引和块间索引），来加快认证速度。

块内索引

之前为了简单起见，假设每个区块仅为存储一个对象。正常来说，每个区块通常存储多个对象。可以对每个对象重复应用single-object algorithm算法来确保查询的完整性，然而，这会导致验证复杂度与对象数量成线性关系。此外，可以观察到，如果两个对象共享某些共同的属性值，它们可能由于相同的部分查询条件而对某些查询不匹配。因此，为了减少校对和验证开销，提出了一个块内索引，可以聚合多个对象并提高性能。

上图显示了一个在区块链上带有块内索引的区块。它将每个对象的ObjectHash和AttDigest组织成一个二叉的Merkle树。因此区块头由PreBkHash, TS, ConsProof, MerkleRoot组成，其中MerkleRoot是二叉默克尔树的根哈希。每一个树节点有三个字段：孩子结点的哈希值(表示为 $hash_{i}$ ，用来构成MHT)，多重集属性（用 $W_{i}$ ）表示，属性多重集的累加值(用 $AttDigest_{i}$ 表示)。它们是从孩子节点计算的，如下所示。
(块内索引非叶节点)???用hash(·) 表示哈希加密函数，’ | '是字符串连接操作符， acc(·)是多集累加器, $n_{l}$ 和 $n_{r}$ 分别是结点n的左孩子和右孩子。非叶节点n的字段定义为:

? $W_{n}$ = $W_{n_{l}}$ ∪ $W_{n_{r}}$ ? （对孩子节点的多重集取并集作为本节点的多重集属性）
? $AttDigest_{n}$ = acc( $W_{n}$ )? （具有可聚合的属性，自底向上层层聚合到根节点）
$hash_{n}$ = $hash$ ( $hash$ ( $hash_{n_{l}}$ | $hash_{n_{r}}$ ) | $AttDigest_{n}$ )? ? （注意 下标都是n）

(块内索引叶子节点)? ?叶节点的字段与底层对象的字段相同。

当构建块内索引时，我们希望实现最大的验证效率。也就是说，目标是在查询处理过程中最大化修剪不匹配对象的机会。一方面，这意味着应该找到一个集群策略，使得对于用户的查询，节点不匹配的机会最大。换句话说，应该使每个节点下的对象的相似性最大化。另一方面，平衡二叉树是最优选择，因为它可以提高查询效率。因此，以自下而上的方式基于区块的数据对象构建块内索引（由矿工）。首先，块中的每个数据对象被分配给一个叶节点。接下来产生最大 Jaccard 系数（| $W_{n_{l}}$ ∩ $W_{n_{r}}$ | / | $W_{n_{l}}$ ∪ $W_{n_{r}}$ |）的叶子结点被迭代合并。这两个合并的树节点用于在上层创建一个新的非叶节点。这个过程在每个级别中重复，直到创建根节点。最后由 $hash_{r}$ 分配的Merkle-Root 被写作区块头的组件之一。

使用上述块内索引，SP可以将查询处理为树搜索。从根节点开始，如果当前节点的属性多集满足查询条件，则将进一步研究其子树。同样，相应的AttDigest被添加到VO中，它将在结果验证期间用于重建MerkleRoot。另一方面，如果多集不满足查询条件，则意味着所有底层对象都不匹配。在这种情况下，SP将调用ProveDisjoint(·)和相应的AttDigest来生成不匹配的证明。直到到达叶子结点，多集满足查询条件的对象是匹配对象，将作为查询结果返回。（不管查询条件匹配与否，都会在VO中返回AttDigest，用于用户端重构Merkleroot）

比如，来自用户的布尔型查询是 “Sedan”∧ (“Benz”∨“BMW”) 。查询过程只是将索引从根节点遍历到叶节点。查询结果为{ $o_{1}$ }。

SP返回的VO包括{? $AttDigest_{r}$ ?, ? $AttDigest_{5}$ ?,? $hash_{2}$ , π $_{2}$ , {“Audi”}, $AttDigest_{2}$ ?, ? $hash_{6}$ , π $_{6}$ , {“Van”}, $AttDigest_{6}$ ?}。这里π $_{2}$ 和π $_{6}$ 分别是不匹配节点N $_{2}$ 和N $_{6}$ 的两个不相交证明（图6用阴影表示）。注意： $AttDigest_{r}$ 和 $AttDigest_{5}$ 将在结果验证时用于MerkleRoot的构建。

在用户方面，不匹配验证通过使用VO中的 $AttDigest$ 、不相交集、证明π来调用VerifyDisjoint(·)进行。此外，为了验证结果的可靠性和完整性，用户需要重新构造MerkleRoot，并将其与从块头读取的MerkleRoot进行比较。

在本例中，首先，使用?π $_{2}$ , $AttDigest_{2}$ , {“Audi”}? 和 ?π $_{6}$ , $AttDigest_{6}$ , {“Van”}?调用VerifyDisjoint(·) 来证明?N $_{2}$ 和N $_{6}$ 确实不匹配查询。然后，用户使用返回的结果计算 $hash$ ( $o_{1}$ )，根据VO计算? $hash_{5}$ = $hash$ ( $hash$ ( $o_{1}$ ) | $hash_{2}$ | $AttDigest_{5}$ )， $hash_{r}$ = $hash$ ( $hash_{5}$ | $hash_{6}$ | $AttDigest_{r}$ )。最后，用户根据区块头中的MerkleRoot检查新计算的哈希值 $hash_{r}$ 。（查询用户作为轻节点，只存储块头数据， $W_{i}$ 字段保存在作为全节点的矿工和SP中，不会浪费用户的存储空间。用户验证时直接使用SP返回的VO中的AttDigest进行计算即可。）

块间索引

?除了同一块内的相似对象之外，由于相同的原因，块间的对象也可能共享相似性并且不匹配查询。论文构建了一种利用跳过列表来进一步优化查询性能的块间索引。

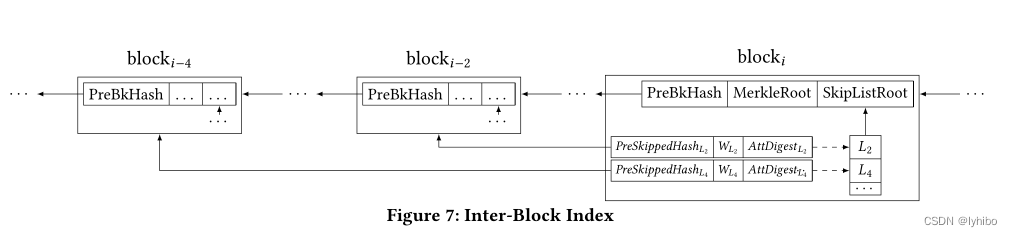
块间索引由多个跳过组成，每个跳过都跳过指数数量的先前块。例如，该列表可能会跳过本块前面的 2、4、8、··· 块。对于每个跳过，它维护三个组件：所有跳过的块的哈希（用 $PreSkippedHash _{L_{k}}$ 表示）、跳过的块的属性多集的总和（用 $W _{L_{k}}$ 表示）和相应的累积值 w.r.t. $W _{L_{k}}$ （用 $AttDigest _{L_{k}}$ 表示）。这里使用属性多集的总和来启用后面的在线聚合身份验证。最后，使用额外字段 $SkipListRoot$ 将块间索引写入块中，其定义为：

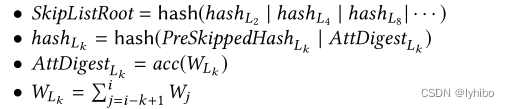
在查询处理期间，合格的跳过可以用于表示由于相同的不匹配原因而对查询结果没有贡献-的多个区块。因为用户可以避免访问这些跳过的块，所以可以降低验证成本。

带有块间索引的查询处理过程从查询时间窗口中的最新块开始。我们将跳跃列表从最大跳过次数迭代到最小跳过次数。如果一个跳过 $W_{L_{i}}$ 的多集不匹配查询条件，则意味着当前块和前i个块之间的所有跳过块都不包含匹配结果。因此，调用ProveDisjoint(·) 然后输出不匹配证明π $_{i}$ 。然后将 ? $PreSkippedHash _{L_{i}}$ , π $_{i}$ , ? $_{i}$ , $AttDigest _{L_{i}}$ ? 加入到VO中。用户可以使用该证明来验证跳过的块确实与查询不匹配。与此同时，除 $hash_{L_{i}}$ 之外的其他哈希值也都被添加到VO中。如果我们在迭代过程中没有发现不匹配的块，当前区块调用IntraIndexQuery(·) ，前一个区块也将被检查。如果我们成功找到不匹配跳过，则接下来将检查相应的前一块。递归调用函数InterIndexquery（·），直到完成检查查询窗口中的所有区块。注意，可以组合块内索引和块间索引来最大化性能，因为它们不冲突。

在线批量验证

所提出的块内索引试图用某种方式将同一区块内的对象聚集在一起来最大化提高验证不匹配对象的效率。然而，在不同块或甚至同一块的不同子树中索引的一些对象/节点也可能有相同的不匹配原因。因此，在线聚合这样的对象/节点对于更有效的校对是有益的。为此，引入的Sum(·) 原语?，Sum(·) 原语在给定多个累加值时输出聚合多重集的累加值。

在图6所示示例中，假设O2和O4共享查询条件不匹配的相同原因(“Benz”)。 ?SP 可以返回π = ProveDisjoint( $W_{2}$ + $W_{4}$ ，{“Benz”}，pk) 以及? $AttDigest_{2,4}$ = Sum(acc( $W_{2}$ ),acc( $W_{4}$ ))。用户可以用VerifyDisjoint( $AttDigest_{2,4}$ ，acc({“Benz”})，π，pk)来证明这两个对象在一批中不匹配。

5 可订阅的查询索引

订阅查询由查询用户注册，并持续处理，直到取消注册为止。当SP看到新确认的区块时，需要将结果与VO一起发布给注册用户。首先提出一个查询索引，以有效地处理大量订阅查询。然后，开发了一个延迟认证优化，延迟不匹配的证明以减少查询验证成本。订阅查询总体上可以分为三步：

（1）服务提供者收集用户的查询语句，建立索引。

（2）当有数据对象到来，就通过索引查找所有满足条件的查询。

（3）将该数据对象发给对应的用户，同时发送不匹配的数据对象的不匹配证明。

可扩展处理的查询索引

大部分查询处理开销来自于SP上的不匹配对象生成证据。对于不同的订阅查询，不匹配的对象可能有相同的不匹配原因。因此，这种查询可以共享不匹配证明。论文提出在订阅查询上构建一个倒置前缀树，称为IP树。它本质上是一个前缀树，引用了数字范围条件和布尔集合条件的倒排文件。

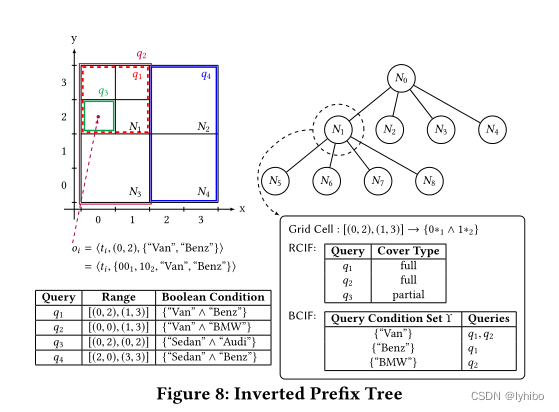
前缀树组件：IP-Tree是基于每个树节点由CNF布尔函数表示的网格树构建的，是为了索引所有订阅查询的数字范围。例如，图8中对应于左上角单元格([0，2]，[1，3])的网格节点 $N_{1}$ 由{ $0*_{1}$ ∧ $1*_{2}$ }表示。前缀树的根节点覆盖了所有订阅查询的整个范围空间。?

倒排文件组件:?IP-Tree的每个节点都与一个倒置文件相关联，该反向文件是基于该节点下索引的订阅查询而构建的。每个反向文件有两个子组件：
?范围条件倒排文件(RCIF). RCIF中的每个条目都有两个属性: 查询 $q_{i}$ 及其覆盖的类型(全部或者部分)。RCIF中的所有查询都与结点的数字空间S相交。覆盖的类型显示 $q_{i}$ 完全覆盖还是部分覆盖S。RCIF函数用于检查数值范围条件的不匹配。
?布尔条件倒排文件(BCIF). BCIF函数只记录完全覆盖结点空间的查询。BCIF中的每个条目由两个属性组成：查询条件集?和相应的查询。BCIF用于检查布尔设置条件的不匹配。

以图8为例说明如何构建IP-Tree。它是由SP以自上而下的方式构建的。首先创建根节点，并将所有查询作为部分覆盖查询添加到它的RCIF中。然后分割根节点并创建四个等距的子节点。对于每个子节点，如果一个查询完全或部分覆盖了该节点的空间，它将被添加到该节点的RCIF中。同样，一个全覆盖查询的等价集将被添加到节点的BCIF中。以 $N_{1}$ 为例。查询 $q_{1}$ 和 $q_{2}$ 完全覆盖了这个节点，查询 $q_{3}$ 仅部分覆盖了它。因此，RCIF包含三个交叉查询 $q_{1}$ 、 $q_{2}$ 和 $q_{3}$ 。 $q_{1}$ 和 $q_{2}$ 的涉及的类型是完整， $q_{3}$ 的类型是部分。对于 $N_{1}$ 的BCIF，? $q_{1}$ 和 $q_{2}$ ?共享同样的集合{“Van”}，集合{“Benz”}和{“BMW”}分别对应着? $q_{1}$ 和 $q_{2}$ ?的查询。接下来，由于 $q_{3}$ 只部分覆盖了 $N_{1}$ ，我们进一步将 $N_{1}$ 分裂成四个部分。由于 $q_{3}$ 全部覆盖了 $N_{7}$ ，它被添加到 $N_{7}$ 的RCIF和BCIF中。当在任何叶节点中没有找到部分查询时，算法终止。当一个查询被注册或注销时，更新IP-Tree的节点与查询的数值范围相对应。如果有必要，也可以拆分或合并树节点。注意，为了防止树变得太深，当树的深度达到某个预定义的阈值时，将会切换回没有IP-Tree的情况。

使用IP-Tree索引，可以将订阅查询作为树遍历处理。当一个新的对象O到达时，IP树沿着从根到覆盖O的叶节点的路径被遍历。对于遍历路径上的任何节点 $n_{q}$ ，可以从 $n_{q}$ 的RCIF中找到相关的查询。这些查询可以分为三类:

(1)一个等价集在 $n_{q}$ 的BCIF上匹配对象O的全覆盖查询（因此，这个查询的结果是O被添加）。?

(2)一个等价集在 $n_{q}$ 的BCIF上不匹配对象O的全覆盖查询（因此，将调用ProveDisjoint(·)，并为该查询生成一个不相交证明）。?

(3)部分覆盖查询(无需进一步操作)。

此外，识别出现在 $n_{q}$ 的父节点但不在 $n_{q}$ 的RCIF查询。接下来， $n_{q}$ 的子节点将被处理，并且这个过程继续，直到到达一个叶节点或者所有查询都被分类为匹配或不匹配。考虑一个新的对象Oi = ? $t_{i}$ ,(0,2), {“Van”,“Benz”}? = ? $t_{i}$ , { $00_{1}$ , $10_{2}$ ,“Van”,“Benz”}? 在图8中展示。在 $N_{1}$ ， $q_{1}$ 被归类为匹配查询， $q_{2}$ 和 $q_{4}$ 分别因为布尔集合条件和数值范围条件而不匹配。而 $q_{3}$ 直到检查 $N_{1}$ 的子节点 $N_{7}$ 才被确认为不匹配。

思路能够很轻易的由区块内索引索引的对象的新块被推导出来。我们从块内索引的根开始，对于结点 $n_{b}$ 的任何索引，将其视为一个超级对象，并应用上述查询处理过程。唯一的区别是，如果一个全覆盖查询被归类为匹配，我们不能立即返回当前节点作为查询结果，而是进一步递归检查其子节点，直到到达叶节点。

惰性认证

在前面的部分中，新的区块被确认时，结果和证明被立即发布给注册用户。特别是，即使查询没有匹配结果，仍然计算并发送不匹配的证明。这种方法适用于实时应用程序。对于没有此类实时要求的应用程序，提出了一个延迟认证优化，其中SP在存在匹配对象时才会返回结果（或自上次结果以来的时间已通过阈值）。

在这种方法中，VO应该证明当前对象是匹配的，并且自最后一个结果以来的所有其他对象都与查询不匹配。为了实现这一点，只需等待匹配结果，并调用一个时间窗口查询来动态计算不匹配的证据。然而，这种方法只能分别为每个查询生成不匹配的证明，不能利用不同订阅查询共享的证明。此外，这种方法将校对的负担全部留给有匹配结果的时候。为了解决这些问题，提出了一种新的方法，利用块间索引来增量生成不匹配证明。

使用块间索引来回答订阅查询与使用时间窗口查询完全不同。原因是可以反向遍历区块链，并使用跳过列表在时间窗口查询中聚合证据。但是，对于订阅查询不能这样做，因为新的块尚不可用，并且我们不知道未来的对象是否会共享相同的不匹配条件。因此，引入一个堆栈，以便于跟踪共享相同不匹配条件的到达块。基本思想是使用跳跃列表来找到最大跳过距离 $L_{i}$ ，这样它就覆盖了m个堆栈顶部的元素。区块的AttDigest被 $AttDigest_{L_{i}}$ 替代。不相交的证明可以通过调用ProofSum()在线聚合。例如，堆栈中有两个不匹配的 $block_{i}$ 和 $block_{i-1}$ 并且跳过距离为2。然后，SP可以用一个从ProofSum(π $_{i}$ ，π $_{i-1}$ )计算的聚合证明来替换它们的证明。这样，当找到匹配结果时，SP不需要从头计算集合不相交证明。

6 总结

在文献中首次研究了区块链数据库的可验证查询处理问题。提出了vChain框架来保证轻量级用户布尔范围查询的完整性。开发了一种新的基于累加器的自动数据挖掘方案，该方案将数字属性转换为集值属性，从而能够在任意查询属性上进行动态聚合。在此基础上，设计了两个数据索引，即基于树的块内索引和基于跳转列表的块间索引，以及一个基于前缀树的订阅查询索引，并进行了一系列优化。