IEEE INTERNET OF THINGS JOURNAL, VOL. 6, NO. 3, JUNE 2019
文章目录
摘要
智慧社区(SC)作为能源互联网(IoE)的重要组成部分,可以促进分布式可再生能源和电动汽车(EV)在智能电网中的集成。然而,由于不受信任和不透明的能源市场带来的潜在安全和隐私问题,如何优化调度SC中具有不同能耗偏好的电动汽车的充电行为成为一个巨大的挑战。
在本文中,我们提出了一种基于合约的能源区块链,用于在SC中对EV进行安全充电。
- 首先,引入了一个被许可的能源区块链系统,以通过执行智能合约来实现电动汽车的安全充电服务。
- 其次,提出了基于假设的委托拜占庭容错共识(DBFT)算法,以有效地实现区块链中的共识。
- 第三,基于合约理论,对最优合约进行了分析和设计,以满足电动汽车对能源的个性化需求,同时使运营商的效用最大化。
- 此外,还提出了一种新的能源分配机制,将有限的可再生能源分配给电动汽车。
- 最后,通过与其他传统方案的比较,进行了大量的数值计算,以评估和证明所提方案的有效性和效率。
关键词:合约理论,电动汽车,能源区块链,能源互联网,智慧社区。
介绍
可再生能源(RES)和电动汽车(EV)在缓解化石燃料危机和减少气体排放方面具有巨大潜力,这吸引了全世界的关注。
为了整合和协调大量分布式RES和EVs,能源互联网(IoE)已成为提高能源效率和可持续性的一种有前途的创新方法。
此外,配备RES的智能社区(SC)可以被视为IoE的重要组成部分,它可以实现内部能源的生成、存储和分配,并可以与外部能源实体进行能源交换,例如电网和电动汽车。在SC中,最好使用分布式RES以经济高效的方式对一组电动汽车充电。
微电网是由分布式可再生能源(如太阳能、风能、水力发电等)供电的小型电力系统,已被证明是将本地可用可再生能源整合到智能电网的可行有效策略。在与微电网集成的SC中,它允许能源供应商和消费者直接交易能源。这种本地电力交易不仅减少了输电过程中的电力损失,还减轻了电网的负担。因此,SC的电动汽车充电框架涉及三个能源方,即电网、微电网和电动汽车。
存在的问题:
- 大部分文献仅考虑了电动汽车与微电网或电网之间的双向互动,不能直接应用于SC中电动汽车的充电管理。
- 电动汽车用户对SC中的各种能源(清洁能源、传统能源或两者的混合)有不同的充电偏好。(因此既需要电网提供传统能源,也需要微店网提供清洁能源)
能源市场的恶意运营商将通过各种恶意手段严重威胁电动汽车的安全和隐私,例如隐私泄露、伪造、节点入侵、广告欺诈收费服务等。区块链通过使用不可变账本、加密货币和执行智能合约,为分布式网络中无可信代理的安全能源交易提供了独特的技术。然而,广泛使用的工作证明共识协议浪费了大量精力,并且在传统区块链应用程序(如比特币)中的交易确认速度较慢。因此,它不适用于许可的能源区块链。因此,解决电动汽车充电的安全问题仍然是一个公开而重要的问题。
在本文中,为了解决上述问题,我们在SC中开发了一种基于合约理论的电动汽车充电方案,该方案由许可的区块链技术提供安全保障。
- 首先,通过在SC中引入一个新的许可能源区块链系统,预选的EV可以公开审计和共享交易记录,而无需依赖可信的中介。
- 随后,提出了一种基于信誉的委托拜占庭容错(DBFT)共识算法,以有效地在允许的能量块链中达成一致。
- 此外,基于合约理论,垄断经营者分析和设计了最优合约,以满足电动汽车的个人能源需求偏好。
- 最后,提出了一种新的能量分配机制,在最大化运营商效用的同时,为电动汽车分配有限的可再生能源。
贡献
- 首先,基于许可的区块链技术,我们在智慧社区的能源区块链系统中提出了一个安全电动汽车充电框架,其中预选的EVs可以公开审计和共享交易记录,而不依赖于可信的中介。为了降低在能源受限的EVs中建立区块链的成本,我们提出了一种基于信誉的DBFT共识算法。
- 第二,我们利用合约博弈模型来模拟信息不对称情况下,集成商和电动汽车之间的决策过程。在我们提出的的合约博弈中,聚合者设计合约菜单,其中包含针对所有类型电动汽车的交易策略。在我们的框架内,电动汽车可以选择传统能源、清洁能源或两者的混合,以满足其个人的能源偏好,同时最大限度地提高运营商的效用。
- 第三,我们提出了一种动态最优合约分配和能源分配算法,以实现最优合约,并解决了“由于可再生能源供应的间歇性和不稳定,所有电动汽车的最优策略可能并不总是满足”的问题。我们进行了大量的仿真实验,以验证所建议方案的有效性和效率。与传统方案相比,我们的方案可以提高运营商和电动汽车的效用。
相关工作
A. 智慧社区
B. 能源区块链
C. 电动汽车充电调度
系统模型
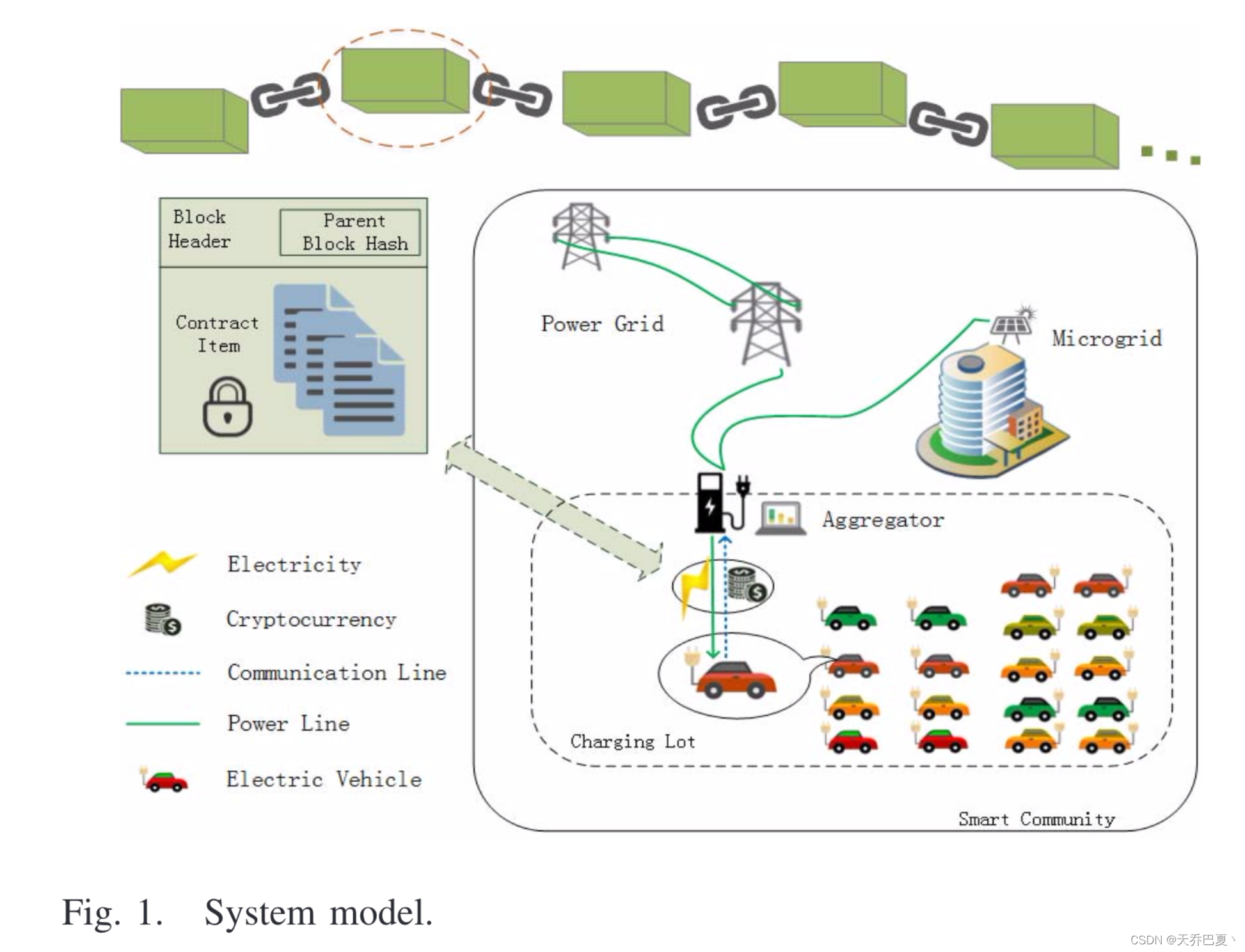
A. 网络模型
- 电动汽车电力零售商(Aggregator):电力零售商可以从电网和本地微电网(即光伏(PV)系统)获取能量。一方面,该它负责管理太阳能电池板,并将收集的太阳能出售给电动汽车。另一方面,它以单价从电网购买能源,并将传统能源出售给电动汽车。
- 电动汽车(EVs):作为能源消费者,具有不同的能源消费偏好(比如可以从电网或PV系统购买能源,也可以从SC的混合系统购买能源),电动汽车表示为 L = ( 1 , . . . i , . . . I ) L = (1,...i,...I) L=(1,...i,...I),定义 θ i θ_i θi?为电动汽车 i i i的能源消费偏好,对应的是 Θ = ( θ 1 , θ 2 , . . . θ I ) \Theta=(θ_1,θ_2,...θ_I) Θ=(θ1?,θ2?,...θI?)。
- 智能电表(Smart Meters):每辆电动汽车中都有一个内置的智能电表记录能耗量,以验证交易是否已完成,从而授权付款。
- 微电网(Microgrid): 光伏(PV)系统作为SC的本地微电网,由安装在社区建筑屋顶上的多个太阳能电池板组成。
B. 效用函数
垄断运营商为消费者提供了一组能源 { x ( θ i ) ∈ Ω } \{ x(\theta_i)\in \Omega\} {x(θi?)∈Ω}和相应的价格 { π ( θ i ) ∈ Π } \{ \pi(\theta_i)\in \Pi\} {π(θi?)∈Π},由能源和价格组成的合约项目集合定义为: Ψ = { ( x ( θ i ) , π ( θ i ) ) ∣ ? θ i ∈ Θ } \Psi=\{(x(\theta_i),\pi(\theta_i))|\forall \theta_i \in \Theta\} Ψ={(x(θi?),π(θi?))∣?θi?∈Θ}。
显然,电动汽车的能源需求既不能为负,也不能为无穷大,即有: Ω = { x ( θ i ) ∣ 0 ≤ x ( θ i ) ≤ ( C i / η i ) } \Omega=\{x(\theta_i)|0\leq x(\theta_i) \leq (C_i/\eta_i)\} Ω={x(θi?)∣0≤x(θi?)≤(Ci?/ηi?)},这里 η i \eta_i ηi?表示EV i i i的充电效率, C i C_i Ci?表示EV i i i的容量。此外,电动汽车可以决定是否从零售商购买电力,如果 x ( θ i ) = 0 x(\theta_i) = 0 x(θi?)=0表示没有购买,也就不需要支付任何价格的费用。
在能源市场中,电动汽车的效用函数应该是其能源需求的凹函数,而不是递减函数。如果EV
i
i
i选择的合约项目为
(
x
(
θ
i
)
,
π
(
θ
i
)
)
(x(\theta_i),\pi(\theta_i))
(x(θi?),π(θi?)),那么它的效用函数可以定义为:
U
(
θ
i
,
x
(
θ
i
)
)
=
V
(
θ
i
,
x
(
θ
i
)
)
?
π
(
θ
i
)
(3)
U(\theta_i,x(\theta_i)) = V(\theta_i,x(\theta_i)) - \pi(\theta_i) \tag{3}
U(θi?,x(θi?))=V(θi?,x(θi?))?π(θi?)(3)
其中,
V
(
θ
i
,
x
(
θ
i
)
)
V(\theta_i,x(\theta_i))
V(θi?,x(θi?))是EV
i
i
i从能源消耗中获得的满意度系数。
基于论文【31,47,48】,目前自然对数函数在能源购买者效用建模中已经被广泛接受。因此,我们使用对数函数来建模电动汽车满意度与需求之间的关系,包括清洁能源需求和传统能源需求,如论文【49】所示:
V
(
θ
i
,
x
(
θ
i
)
)
=
α
l
n
[
1
+
ω
θ
i
x
(
θ
i
)
+
ω
0
(
1
?
θ
i
)
x
(
θ
i
)
]
(4)
V(θ_i,x(θ_i))=αln[1+ωθ_ix(θ_i)+ω_0(1?θ_i)x(θ_i)] \tag{4}
V(θi?,x(θi?))=αln[1+ωθi?x(θi?)+ω0?(1?θi?)x(θi?)](4)
式中,
α
α
α是非负满意度系数,
ω
ω
ω是代表可再生能源发电清洁度的环境友好系数,而
ω
0
ω_0
ω0?表示传统化石能源的清洁度。一般来说,假设
ω
>
ω
0
>
0
ω>ω_0>0
ω>ω0?>0。很容易看出
(
[
?
V
(
θ
i
,
x
(
θ
i
)
)
]
/
?
θ
i
)
≥
0
,
(
[
?
V
(
θ
i
,
x
(
θ
i
)
)
]
/
?
x
(
θ
i
)
>
0
([?V(θ_i,x(θ_i))]/?θ_i)≥0,([?V(θ_i,x(θ_i))]/?x(θ_i)>0
([?V(θi?,x(θi?))]/?θi?)≥0,([?V(θi?,x(θi?))]/?x(θi?)>0,以及
(
[
?
2
V
(
θ
i
,
x
(
θ
i
)
)
]
/
?
x
(
θ
i
)
2
)
<
0
([?^2V(θ_i,x(θ_i))]/?x(θ_i)^2)<0
([?2V(θi?,x(θi?))]/?x(θi?)2)<0。如果效用为负值,EV
i
i
i将选择合约项
(
x
(
θ
i
)
=
0
,
π
(
θ
i
)
=
0
)
(x(θ_i)=0,π(θ_i)=0)
(x(θi?)=0,π(θi?)=0)。很明显,
V
(
θ
i
,
0
)
=
0
,
U
(
θ
i
,
0
)
=
0
V(θ_i,0)=0,U(θ_i,0)=0
V(θi?,0)=0,U(θi?,0)=0。
这里,我们将 R ( x ( θ i ) ) R(x(θ_i)) R(x(θi?))定义为从EV i i i的合约项 ( x ( θ i ) , π ( θ i ) ) (x(\theta_i),\pi(\theta_i)) (x(θi?),π(θi?))中获得的电力零售商的效用。我们有: R ( x ( θ i ) ) = π ( θ i ) ? C ( θ i , x ( θ i ) ) (5) R(x(θ_i))=π(θ_i)?C(θ_i,x(θ_i)) \tag{5} R(x(θi?))=π(θi?)?C(θi?,x(θi?))(5)显然,零售商不会接受负影响,也就是说满足: Π = { π ( θ i ) ∣ π ( θ i ) ≥ C ( θ i , x ( θ i ) ) } \Pi=\{π(θ_i)|π(θ_i)≥C(θ_i,x(θ_i))\} Π={π(θi?)∣π(θi?)≥C(θi?,x(θi?))}。
成本函数由发电成本、从电网购买电力的费用以及政府提供的补贴组成,可以表示为:
C
(
θ
i
,
x
(
θ
i
)
)
=
(
c
p
v
?
r
p
v
)
θ
i
x
(
θ
i
)
+
p
g
(
1
?
θ
i
)
x
(
θ
i
)
+
c
0
(6)
C(θ_i,x(θ_i))=(c_{pv}?r_{pv})θ_ix(θ_i)+p_g(1?θ_i)x(θ_i)+c_0 \tag{6}
C(θi?,x(θi?))=(cpv??rpv?)θi?x(θi?)+pg?(1?θi?)x(θi?)+c0?(6) 其中
c
p
v
c_{pv}
cpv?和
r
p
v
r_{pv}
rpv?分别是太阳能电池板发电的单位成本和单位补贴。
c
0
>
0
c_0>0
c0?>0是固定成本,主要包括交易成本、存储成本等。一般来说,我们假设
0
≤
c
p
v
?
r
p
v
≤
p
g
0≤c_{pv}-r_{pv}≤p_g
0≤cpv??rpv?≤pg?,这意味着可再生能源发电的最终单位成本不超过电网的电力市场价格。然后我们可以得到
(
[
?
C
(
θ
i
,
x
(
θ
i
)
)
]
/
?
θ
i
)
≤
0
,
(
[
?
C
(
θ
i
,
x
(
θ
i
)
)
]
/
?
x
(
θ
i
)
≥
0
([?C(θ_i,x(θ_i))]/?θ_i)≤0,([?C(θ_i,x(θ_i))]/?x(θ_i)≥0
([?C(θi?,x(θi?))]/?θi?)≤0,([?C(θi?,x(θi?))]/?x(θi?)≥0,以及
(
[
?
2
C
(
θ
i
,
x
(
θ
i
)
)
]
/
?
x
(
θ
i
)
2
)
=
0
([?^2C(θ_i,x(θ_i))]/?x(θ_i)^2)=0
([?2C(θi?,x(θi?))]/?x(θi?)2)=0,因此对于电力零售商,所有的效用函数都可以写成:
R
=
∑
i
=
1
I
τ
θ
i
(
π
(
θ
i
)
?
C
(
θ
i
,
x
(
θ
i
)
)
)
(7)
R=\sum_{i=1}^I\tau_{θ_i}(π(θ_i)?C(θ_i,x(θ_i))) \tag{7}
R=i=1∑I?τθi??(π(θi?)?C(θi?,x(θi?)))(7)
其中:
τ
θ
i
\tau_{θ_i}
τθi??表示类型为
θ
i
{θ_i}
θi?的EV数量占EV总数的比例。我们进一步将零售商和特定电动汽车之间能源交易的社会剩余定义为两种公共事业的总和:
S
(
θ
i
,
x
(
θ
i
)
)
=
R
(
x
(
θ
i
)
)
+
U
(
θ
i
,
x
(
θ
i
)
)
=
V
(
θ
i
,
x
(
θ
i
)
)
?
C
(
θ
i
,
x
(
θ
i
)
)
(8)
S(θ_i,x(θ_i))=R(x(θ_i))+U(θ_i,x(θ_i))=V(θ_i,x(θ_i))?C(θ_i,x(θ_i)) \tag{8}
S(θi?,x(θi?))=R(x(θi?))+U(θi?,x(θi?))=V(θi?,x(θi?))?C(θi?,x(θi?))(8)根据(4)和(6),可以得到:
(
[
?
2
S
(
θ
i
,
x
(
θ
i
)
)
]
/
?
x
(
θ
i
)
2
)
<
0
([?^2S(θ_i,x(θ_i))]/?x(θ_i)^2)<0
([?2S(θi?,x(θi?))]/?x(θi?)2)<0,同样,能源市场的整体社会剩余可以写作:
S
=
∑
i
=
1
I
τ
θ
i
(
V
(
θ
i
,
x
(
θ
i
)
)
?
C
(
θ
i
,
x
(
θ
i
)
)
)
(9)
S=\sum_{i=1}^I\tau_{θ_i}(V(θ_i,x(θ_i))?C(θ_i,x(θ_i))) \tag{9}
S=i=1∑I?τθi??(V(θi?,x(θi?))?C(θi?,x(θi?)))(9)为了简单起见,在下面的内容中,分别将
τ
θ
i
,
N
θ
i
,
x
(
θ
i
)
,
π
(
θ
i
)
τ_{θ_i},N_{θ_i},x(θ_i),π(θ_i)
τθi??,Nθi??,x(θi?),π(θi?)改成
τ
i
,
N
i
,
x
i
,
π
i
τ_i,N_i,x_i, π_i
τi?,Ni?,xi?,πi?。
C. 攻击模型
- 恶意的能源供应商:宣传缺乏太阳能的欺诈性收费服务。
- 恶意的能源消费者:电动汽车拒绝付款。
- 恶意的可信第三方:可能会泄漏电动汽车的隐私,也可能为了牟利而篡改电动汽车的信誉值。
能源区块链
A. 智能合约
在区块链上下文中,智能合约是一组驻留在区块链上并且合约参与者都同意的数字承诺。智能合约允许在没有第三方的情况下,在不同的匿名方之间以规定的方式自动执行可信交易。算法1给出了智能合约实现的详细概述:

- Init():系统初始化。在受信任机构注册之后,EV i i i将会得到证书 C e r i Cer_i Ceri?,绑定唯一的 I D i ID_i IDi?和许可号 p N u m i pNum_i pNumi?,加入区块链网络,并获得公钥/私钥对( P K i , S K i PK_i,SK_i PKi?,SKi?) 和 钱包地址 a d d r e s s i address_i addressi?。 每个EV的账户包含:钱包地址 a d d r e s s i address_i addressi?, 账户收支 b a l a n c e i balance_i balancei?,当前信用值 c r i cr_i cri?,信誉值 R e i Re_i Rei?,证书 C e r i Cer_i Ceri?和公钥/私钥对( P K i , S K i PK_i,SK_i PKi?,SKi?) 。(采用非对称加密技术)
- Create():在零售商和车辆EV i分别就合约项目达成同意并且使用其私钥签署之后,create()函数会将新的智能合约部署到区块链。在区块链网络中达成共识后,智能合约将会被成功部署,每个智能合约将会维护一组状态变量,包括:卖方和买方的账户地址( a c c o u n t s , a c c o u n t i account_s,account_i accounts?,accounti?),能源需求 x i x_i xi?,相应的付款 π i \pi_i πi?,交易时间 t T i m e tTime tTime,时间戳 t S t a m p tStamp tStamp和罚款价格 p P r i c e pPrice pPrice。
- Invoke():Invoke函数在达成共识之后被调用。一旦 t > = t T i m e t>=tTime t>=tTime时,合约就会自动执行,并且执行能源交易和财务结算。智能合约将会读取卖房和买房的智能电表( m s , m i m_s,m_i ms?,mi?),分别验证发电量和耗电量。Penalty函数实现必要的罚款。随后,系统将会定期更新区块链的状态账本,比如:买家账户中的余额、卖家账户中的剩余能源以及智能合约中的状态变量。
充电过程简化如下:
- EV通过能源区块链网络与聚合商签订新的智能合约。
- EV将导航到SC的充电站,等待充电。
- 一旦交易条件得到满足,智能合约将会自动执行,并以规定的方式在买卖方之间进行相应的能源和加密货币交换。
B. 共识过程
为了确保每个节点都有整个账本识别版本的副本,应执行公共审计,即共识过程。基于[52],算法2中提出了基于假设的DBFT一致性算法,以有效地在能源块链中达成一致。共识过程需要经历以下步骤:
一、Leader Election:EVs在V2V网络中有两种类型的角色:普通节点和共识节点。每个节点可以投票,去选举代表(共识节点),投票的权重根据其筹码(信誉值)。通过投票选择前M个代表,表示为
[
1
,
.
.
.
m
,
.
.
.
M
]
[1,...m,...M]
[1,...m,...M],基于【52】,假设
M
>
=
3
f
+
1
M>=3f+1
M>=3f+1,其中
f
f
f是V2V网络中的最大恶意节点个数。 领导者p根据以下式子决定:
p
=
(
h
?
v
)
?
m
o
d
?
M
+
1
p= (h-v) \,mod\, M + 1
p=(h?v)modM+1 h是当前块高度,v是视图的索引,v初始化从0开始。
二、Building Block Concurrently:

详细过程如步骤3-17所示,Qm是交易集,Sm是状态集,tx是一个交易记录,Stx是执行交易tx指定的智能合约之后更改的状态。Bm是由节点m创建的本地区块,verifyTx(tx)用于验证交易tx的有效性,simulate(tx)用于模拟执行交易tx指定的智能合约,buildBlock(Qm,Sm)通过交易集Qm和状态集Sm构建本地区块。
当EV和零售商之间签订智能合约时,EV将会将其广播到网络之中。所有共识节点都会收集特定一段时间内的所有交易,并且在交易中继之前去单独验证每个交易。并且验证无效的交易将被丢弃。然后共识节点模拟执行智能合约,并将更改的状态分别记录到其本地状态分类账中。
所有有效的交易都由每个共识节点在一定时间段内收集,按时间戳排序,并发地打包成块。每个区块都包含到前块的加密哈希。在所有非领导者共识节点都已完成此过程后,委派的领导者将在步骤16中广播ProposalMsg,并将其候选块发送给其他共识节点。
和顺序模型【53】(领导者首先构建候选块,然后其他共识节点构建其本地块)相比,本文提出的并发模型,共识节点并行地构建本地块,可以显著缩短验证候选块的时间。
三、Verifying Candidate Block

详细过程如步骤18-42所示,其中
S
p
S_p
Sp?是接收块的状态集,verifyBlock(B)用于验证接收块的有效性,getState(B)则是用于从接收块中获取状态。
每个非领导的共识节点将会将本地状态集和接受块的状态集进行比较,如果验证通过,每个非领导的共识节点将会在步骤25中带上自己的签名,将confirmMsg广播到网络中。否则,将触发视图更改,然后非领导的共识节点将会在步骤34中广播changeviewMsg。 一旦任何共识节点从不同的共识节点中,收到至少 M ? f M-f M?f个相同的 v k v_k vk?,则该轮视图更改完成,并开始进行下一轮的共识过程。如果共识节点m怀疑从领导者p收到的消息,也会触发视图更改,则共识节点、当前领导的信用值将在步骤36中分别被进行更改。
四、Publishing New Block
任何的共识节点,在 Δ T 1 \Delta T_1 ΔT1?收到不少于 M ? f M?f M?f个来自其他不同共识节点的确认消息,便会达成共识并发布新块。然后,每个共识节点m和最终产生区块的领导p’的信用价值将分别增加 Δ 1 \Delta_1 Δ1?和 Δ 2 \Delta_2 Δ2?。达成共识后,新块以线性和时间顺序添加到区块链中,其中包含前一块的加密哈希。任何节点都会将其区块链的本地副本与新区块同步,并为下一轮共识流程做好准备。
根据[52],我们提出的规定 f = ? ( M ? 1 ) / 3 ? f=\left\lfloor(M-1)/3 \right\rfloor f=?(M?1)/3?对包含M个共识节点的系统的容错。
通过执行智能合约,可以在不受信任的能源市场中自动、安全地执行交易过程,即能源和加密货币交换。如果恶意零售商在没有足够RES的情况下发布欺诈性收费服务广告,则将根据智能合约进行相应的处罚。此外,每个交易都记录在区块链中的可识别账本中。
在能源区块链系统中,所有信誉值都记录在区块链中,而不是集中信任中心。
- 一方面,由于巨大的成本,很难对区块链网络中的所有共识节点进行比较,以篡改当前的信誉值。
- 另一方面,由于每个块都与前一块哈希链相连,因此每个块中的历史信誉值和事务都是不可伪造的。
最佳合约设计
在本节中,基于合约理论,我们分析了第四节A中的集成商和每个EV之间的最优合约,以最大化双方的效用。首先,我们提出合约的可行性。然后分析了最优契约。最后,设计了有限能源交易市场中的能源分配机制。
A. 合约制定
根据【54】提出的revelation principle:可行的合约指的是:每个具有特殊偏好的电动汽车可以根据自己类型选择相应的合约项目去最大化其效用。
根据【55】提出的合约理论,可行的合约指的是:所有的类型的电动汽车同时满足以下两个约束条件:
- 个体理性( IR )约束,类型为 θ i \theta_i θi?的EV通过选择合约项目 ( x i , π i ) (x_i, \pi_i) (xi?,πi?)接收到的非负效用。 α l n [ 1 + ( w θ i + w 0 ( 1 ? θ i ) ) x i ] ? π i ≥ 0 ????? ? ? θ i ∈ Θ ? (15) \alpha ln[1+(w\theta_i+w_0(1-\theta_i))x_i]-\pi_i\geq0\,\,\,\,\,\forall\,\theta_i\in\Theta\ \tag{15} αln[1+(wθi?+w0?(1?θi?))xi?]?πi?≥0?θi?∈Θ?(15)
- 激励相容( IC )约束,相比于类型为 θ j \theta_j θj?对应的合约项目,类型为 θ i \theta_i θi?的EV更愿意选择类型为 θ i \theta_i θi?对应的合约项目。 α l n [ 1 + ( w θ i + w 0 ( 1 ? θ i ) ) x i ] ? π i ≥ α l n [ 1 + ( w θ i + w 0 ( 1 ? θ i ) ) x j ] ? π j ????? ? ? θ j ≠ θ i (16) \alpha ln[1+(w\theta_i+w_0(1-\theta_i))x_i]-\pi_i\geq \alpha ln[1+(w\theta_i+w_0(1-\theta_i))x_j]-\pi_j \,\,\,\,\,\forall\,\theta_j\neq\theta_i \tag{16} αln[1+(wθi?+w0?(1?θi?))xi?]?πi?≥αln[1+(wθi?+w0?(1?θi?))xj?]?πj??θj?=θi?(16)
因此,作为合约的设计者,电力零售商为所有类型的电动汽车建立最优合约,以最大化其效用。
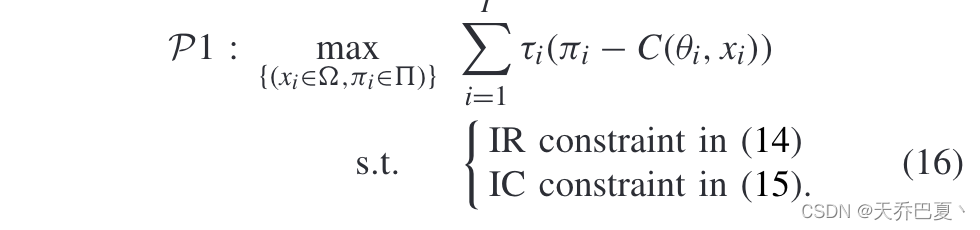
B. 合约的可行性
C. 合约的最优化
D. 能源分配
我们假设在最优合约中,电动汽车充电的可用RES总量足够,即 E r e s ≥ ∑ i = 1 I N i θ i x i ? E_{res}≥∑^I_{i=1}N_iθ_ix^?_i Eres?≥∑i=1I?Ni?θi?xi??,其中E是电动汽车充电所需的总可用太阳能。然而,在实际应用中,SC中的太阳能发电总是有限的,即 E r e s < ∑ i = 1 I N i θ i x i ? E_{res}<∑^I_{i=1}N_iθ_ix^?_i Eres?<∑i=1I?Ni?θi?xi??, 特别是对于有大量电动汽车的系统。因此,应设计适当的能源分配方案,以有效地将有限的可再生能源分配给电动汽车。
这里,每种类型为
θ
i
\theta_i
θi?的EV将会选择由电力零售商设计的最优合约
(
x
i
?
,
π
i
?
)
(x^*_i,\pi^*_i)
(xi??,πi??),根据(5),通过出售能源
x
i
?
x^*_i
xi??来实现零售商的效用:
R
(
x
i
?
)
=
π
i
?
?
C
(
θ
i
,
x
i
?
)
R(x^?_i)=π^?_i?C(θ_i,x^?_i)
R(xi??)=πi???C(θi?,xi??) 我们将
x
i
^
\hat{x_i}
xi?^?定义为类型为
θ
i
θ_i
θi?的社会最优能源需求,即:
x
i
^
=
a
r
g
m
a
x
x
i
S
(
θ
i
,
x
i
)
\hat{x_i} = argmax_{x_i}S(θ_i,x_i)
xi?^?=argmaxxi??S(θi?,xi?),而
S
(
θ
i
,
x
i
)
S(θ_i,x_i)
S(θi?,xi?)是(8)里定义的社会盈余,而
x
i
^
\hat{x_i}
xi?^?可以通过S对
x
i
x_i
xi?求一阶最优性条件获得:
(
[
?
S
(
θ
i
,
x
i
)
]
/
?
x
i
)
=
(
[
?
V
(
θ
i
,
x
i
)
]
/
?
x
i
)
?
(
[
?
C
(
θ
i
,
x
i
)
]
/
?
x
i
)
=
0
([?S(θ_i,x_i)]/?x_i)=([?V(θ_i,x_i)]/?x_i)?([?C(θ_i,x_i)]/?x_i)=0
([?S(θi?,xi?)]/?xi?)=([?V(θi?,xi?)]/?xi?)?([?C(θi?,xi?)]/?xi?)=0。 这里,零售商和电动汽车都是自私与理性的,因此两者可能不会采用社会最优需求。但,最大社会剩余为双方提供了效用总和的上限。零售商从EV i+1中获得的效用和从EV i中获得的效用差异可以描述为:
R
(
x
i
+
1
?
)
?
R
(
x
i
?
)
=
π
i
+
1
?
?
π
i
?
?
C
(
θ
i
+
1
,
x
i
+
1
?
)
+
C
(
θ
i
,
x
i
?
)
=
V
(
θ
i
+
1
,
x
i
+
1
?
)
?
V
(
θ
i
+
1
,
x
i
?
)
?
C
(
θ
i
+
1
,
x
i
+
1
?
)
+
C
(
θ
i
,
x
i
?
)
=
S
(
θ
i
+
1
,
x
i
+
1
?
)
?
S
(
θ
i
+
1
,
x
i
?
)
+
C
(
θ
i
,
x
i
?
)
?
C
(
θ
i
+
1
,
x
i
?
)
\begin{equation*} \begin{aligned} R(x^?_{i+1})?R(x^?_i) &=π^?_{i+1}?π^?_i?C(θ_{i+1},x^?_{i+1})+C(θ_i,x^?_i) \\ &=V(θ_{i+1},x^?_{i+1})?V(θ_{i+1},x^?_i)?C(θ_{i+1},x^?_{i+1})+C(θ_i,x^?_i) \\ & =S(θ_{i+1},x^?_{i+1})?S(θ_{i+1},x^?_i)+C(θ_i,x^?_i)?C(θ_{i+1},x^?_i) \end{aligned} \end{equation*}
R(xi+1??)?R(xi??)?=πi+1???πi???C(θi+1?,xi+1??)+C(θi?,xi??)=V(θi+1?,xi+1??)?V(θi+1?,xi??)?C(θi+1?,xi+1??)+C(θi?,xi??)=S(θi+1?,xi+1??)?S(θi+1?,xi??)+C(θi?,xi??)?C(θi+1?,xi??)??
经过分析,得到
R
(
x
i
+
1
?
)
≥
R
(
x
i
?
)
R(x^?_{i+1})\geq R(x^?_i)
R(xi+1??)≥R(xi??),意味着在最优合约中,零售商可以从类型更高的EV中获得更高的效用。也就是说,零售商可以通过在有限的能源交易市场中将可再生能源销售给更高类型的电动汽车,从而最大限度地发挥其效用。
我们定义
θ
c
∈
Θ
\theta_c\in\Theta
θc?∈Θ作为满足
∑
i
=
c
I
N
i
θ
i
x
i
?
≥
E
r
e
s
∑^I_{i=c}N_iθ_ix^?_i≥E_{res}
∑i=cI?Ni?θi?xi??≥Eres?和
∑
i
=
c
+
1
I
N
i
θ
i
x
i
?
<
E
r
e
s
∑^I_{i=c+1}N_iθ_ix^?_i<E_{res}
∑i=c+1I?Ni?θi?xi??<Eres?的临界类型。零售商将把有限的RES出售给临界类型的电动汽车,因此在有限的能源交易中,最优合约由以下式子给出:
(
x
~
i
,
π
~
i
)
=
{
(
0
,
0
)
,
i
f
θ
i
<
θ
c
(
x
i
?
,
π
i
?
)
,
i
f
θ
i
≥
θ
c
(51)
(\tilde{x}_i, \tilde{\pi}_i) = \begin{cases} (0,0)&,if &θ_i < θ_c\\ (x^*_i,\pi^*_i)&,if&θ_i \geq θ_c \end{cases} \tag{51}
(x~i?,π~i?)={(0,0)(xi??,πi??)?,if,if?θi?<θc?θi?≥θc??(51)
显然,进行有限能源交易的电动汽车类型集合为:
Θ
~
=
{
θ
c
,
θ
c
+
1
,
.
.
.
,
θ
I
}
\tilde{\Theta} = \{θ_c,θ_{c+1},...,θ_I\}
Θ~={θc?,θc+1?,...,θI?}。一定有一部分电动汽车无法从零售商中获取能源,因此,零售商的总体效用将不再使用(7),而是如下:
R
~
=
∑
θ
i
∈
Θ
~
τ
θ
i
(
π
i
?
?
C
(
θ
i
,
x
i
?
)
)
(52)
\tilde{R}=\sum_{\theta_i\in\tilde{\Theta}}\tau_{θ_i}(\pi^*_i-C(\theta_i,x^*_i)) \tag{52}
R~=θi?∈Θ~∑?τθi??(πi???C(θi?,xi??))(52)
这里,提出了一种动态最优合约分配和能源分配算法,以在有限能源交易市场中获得最优合约,如算法3中的步骤12-14所示。

性能评估
A. 仿真配置
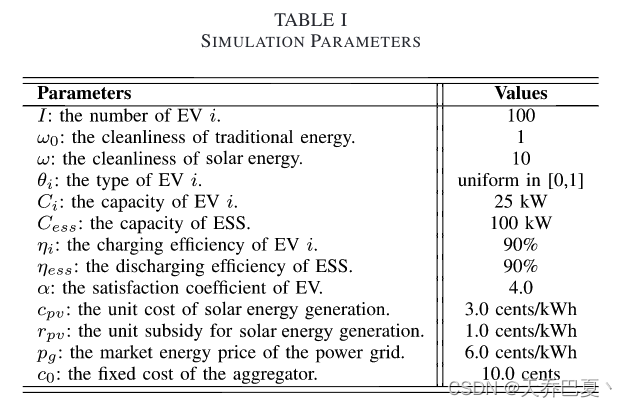
我们考虑了一个电力零售商为社区中的100个电动汽车提供可行合约的场景。电动汽车类型的上限和下限分别设置为1和0。表I中列出了其他参数。
B. 仿真结果
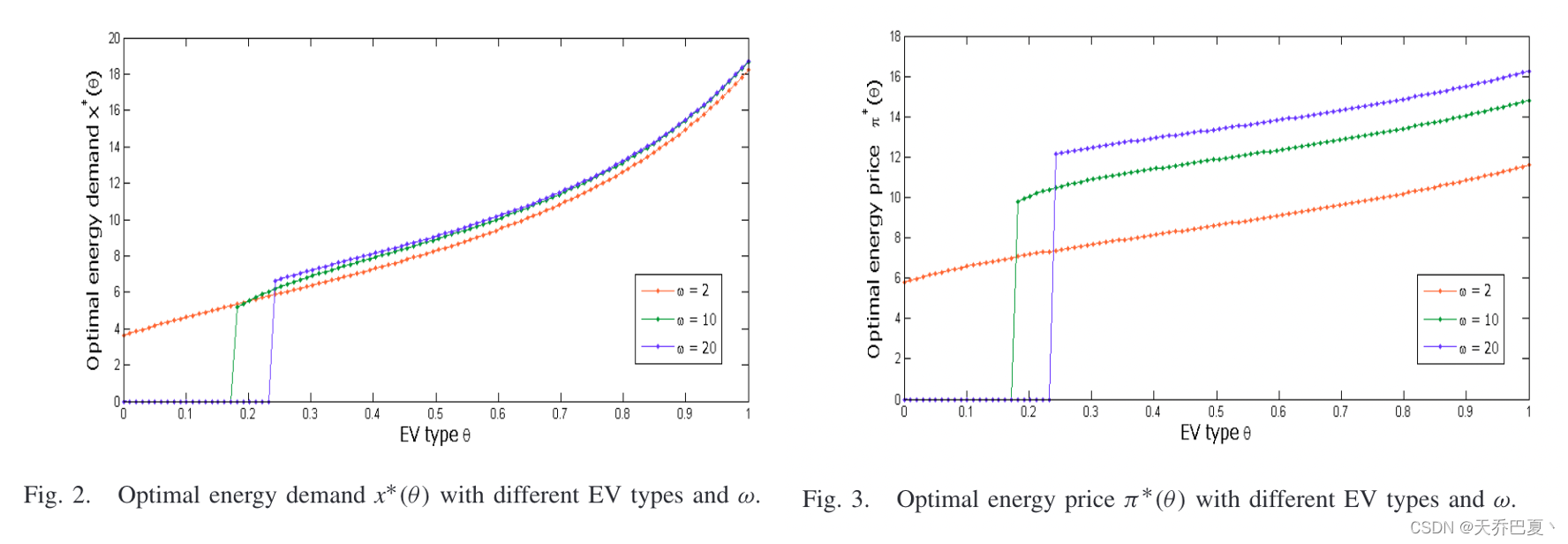
图2和3分别显示了关于各种环境友好系数ω的最优需求和价格。我们观察到,最优合约中的需求和价格都随ω以及类型值θc而增加。原因是ω越高,表示对能源消耗的满意度越高,导致能源需求越高,每个电动汽车应向电力零售商支付的价格也相应越高。
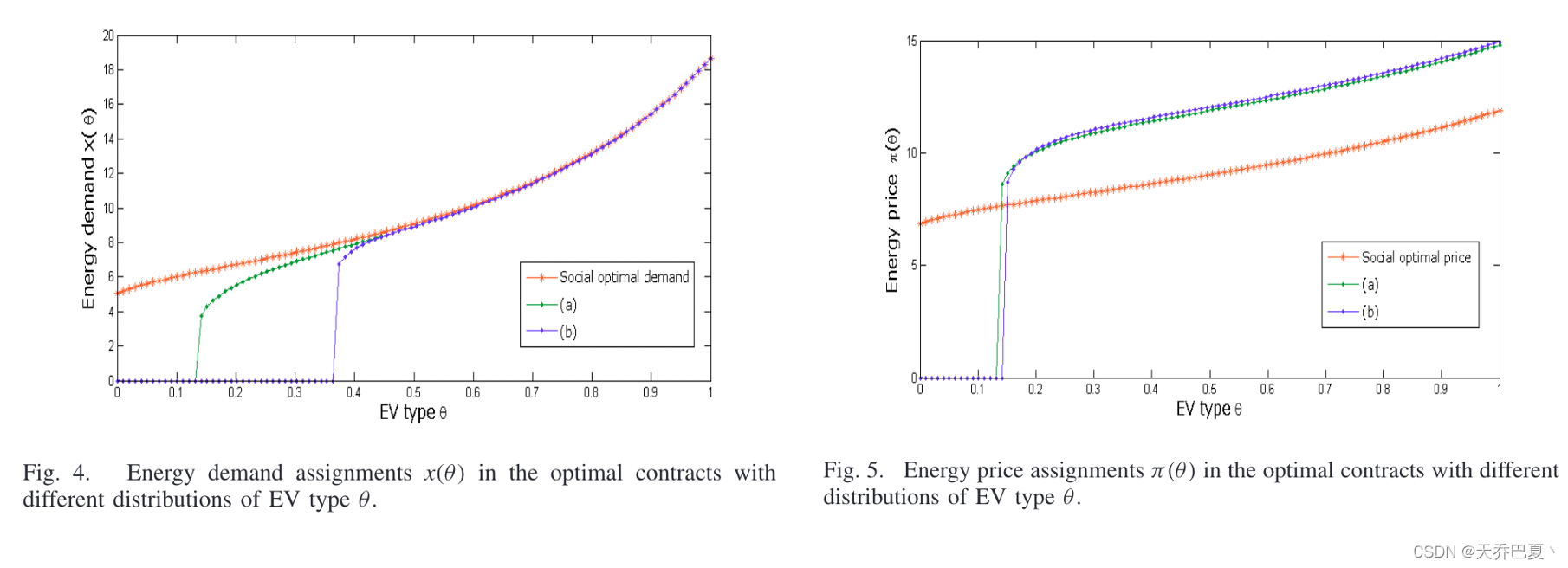
图4和5分别给出了不同电动汽车类型分布下的最优能源需求和价格。在情况(a)中,EV的类型θ是独立的,并遵循均匀分布。在情况(b)中,EV的类型θ是独立的,并遵循参数p=0.5的二项式分布。
图4和5分别表示社会剩余最大化的社会最优需求和相关的社会最优价格。由此可见,非最优合约的需求小于社会最优需求。从经济学角度,与最大化社会剩余相比,电力零售商倾向于减少对低类型电动汽车的需求,并相应提高对高类型电动汽车的价格,以最大化其效用。
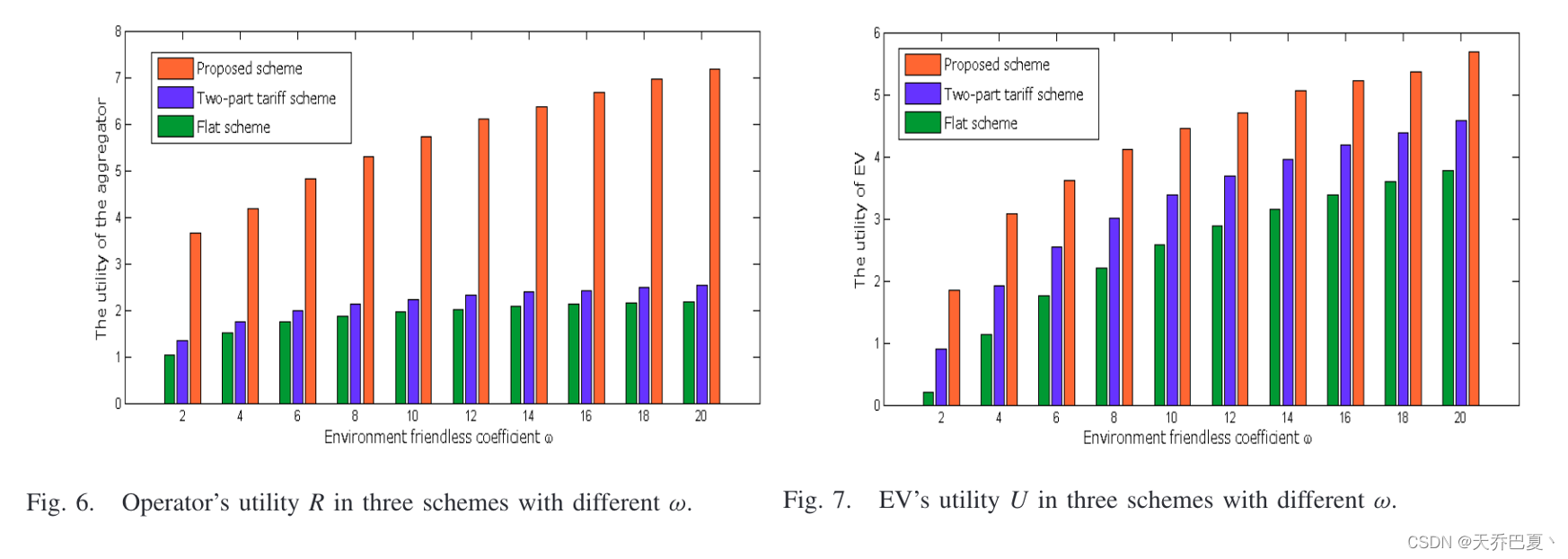
在图6和7中,我们将所提出的方案与两个传统方案进行了比较:T(Two-part tariff scheme)和F(Flast scheme)。
- 在T中,电能需求与其对应价格之间的关系可以表示为 π ( θ ) = P ? x ( θ ) + Z π(θ)=P·x(θ)+Z π(θ)=P?x(θ)+Z,其中运营商只为每种电动汽车指定一个单位电能价格P和一个恒定的充电费Z。
- 在F中,所有类型的电动汽车的单价和充电费都是一样的。
图6和7分别说明了运营商和EV在不同ω下的效用。ω越高,意味着可再生能源清洁发电,电动汽车对能源消耗的满意度越高。
从图6可以看出,与其他两种方案相比,我们的方案获得了更高的电力零售实用性。在拟议方案和T方案中,效用随ω增加而增加,而在F方案中,基本保持不变。
- 在F方案中,所有类型电动汽车的单价都是固定不变的,因此运营商无法调整更高效用的单价。
- 在T方案中,能源价格与能源需求成线性关系,导致运营商效用增长缓慢。
- 在我们的方案中,能源价格和能源需求之间的关系是非线性的,因此运营商的效用相对较高,可以通过设计最优合约来实现最大化。
从图7可以看出,我们的方案比其他两种方案获得了更高的EV效用。三种方案中的效用随着ω的增加而增加。原因是ω越高,电动汽车对能源消耗的满意度越高,导致电动汽车的效用越高。
- 在T方案中,由于单价和收费是可调整的,电动汽车可以相对提高其效用。
- 在我们的方案中,电动汽车的效用可以通过选择最优合约来实现最大化。
根据上述结果,我们的方案可以获得有限能源交易市场的最优合约。此外,在所提出的方案中,电力零售商和EV可以分别有效用上的改进。
结论和未来工作
在本文中,我们为能源区块链系统中的电动汽车提出了一种基于合约的安全充电方案。
- 首先,我们在SC中制定了一个与EV和RES集成的能源区块链系统。
- 其次,提出了一个基于信誉的DBFT算法,以在区块链中有效达成共识。
- 第三,基于合约理论对最优合约进行了分析,以满足电动汽车的能源消费偏好,最大化运营商的效用。
- 最后,仿真结果表明,我们的方案获得的最优合约优于传统方案,以实现运营商和电动汽车的更高效用。
为了将来的工作,我们将进一步将本文扩展到具有竞争影响的多运营商市场。