目录
1. 基础算法
Merkle Patricia Trie,简称 MPT,是 Merkle Tree 和 Patricia Trie 的结合。在介绍 MPT 之前,我们先来看看构成它的基础算法。
1.1 Merkle Tree
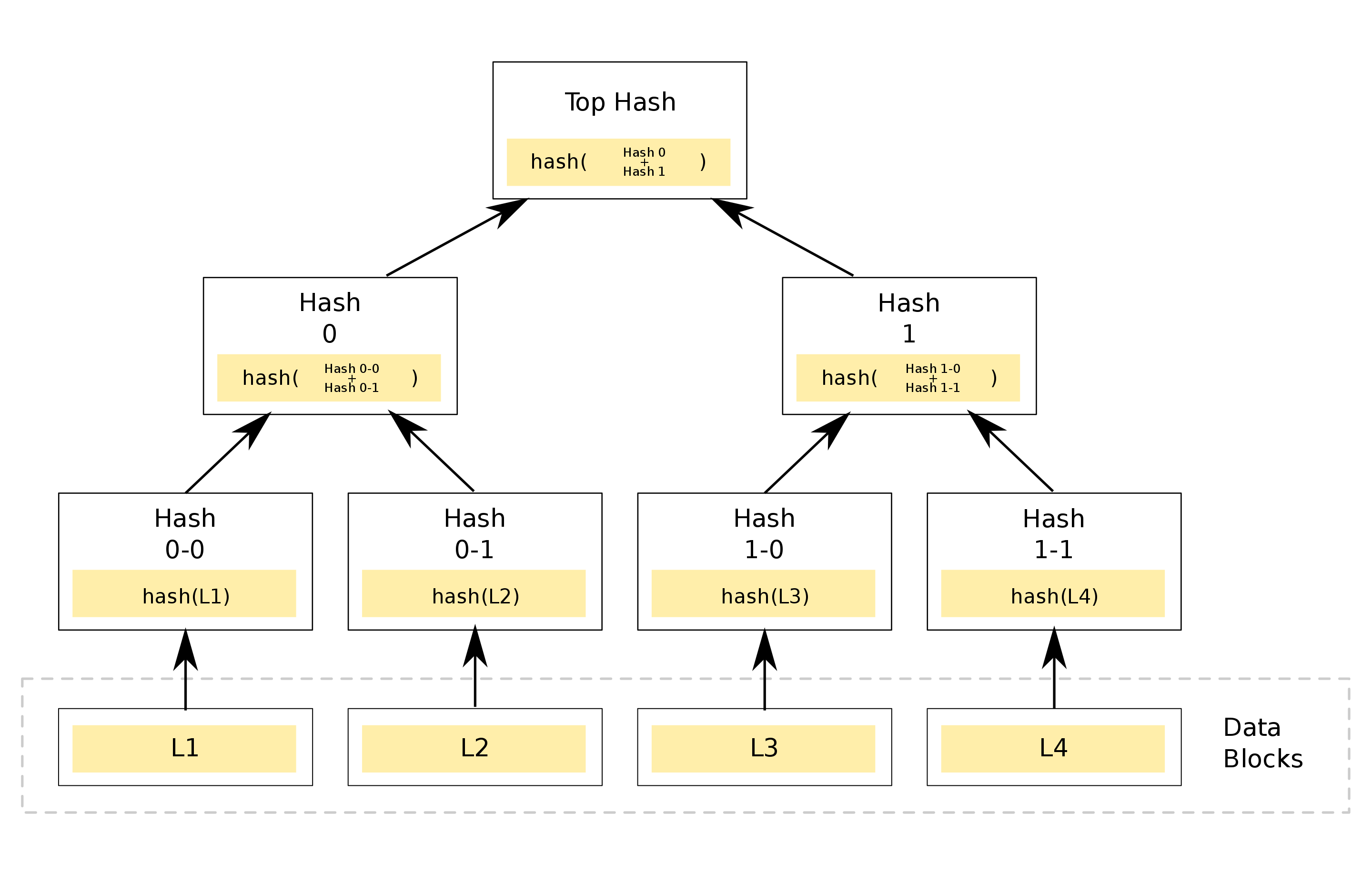
Merkle Tree,默克尔树,表示将数据块做哈希之后,作为叶子节点,再合并多个节点计算哈希,得到新节点,重复以上步骤直到得到一个根节点,形成一个树状结构,如下图:
 ?
?
可见,默克尔树的树根就相当于对所有的数据做了一个哈希,可以用来校验数据的完整性。但这有什么好处呢?为什么不直接把所有数据合并,直接计算一个哈希呢?既然中间多出了这么多冗余的哈希,那自然会有它的用处。实际上,这常被用来做?默克尔证明(Merkle Proof)。一个默克尔证明包含一个数据块、树根、以及经过这个数据块到树根之间的路径的所有哈希。使用默克尔证明可以快速验证一个数据确实存在树中的某个位置。攻击者无法伪造一个默克尔证明,因为根哈希依赖于其他所有节点的哈希,每一个节点的修改都会导致根哈希不一致。
默克尔证明最初被应用在比特币中,区块链中每个区块的交易计算哈希并形成一棵默克尔树,并将树根存储在区块头中。
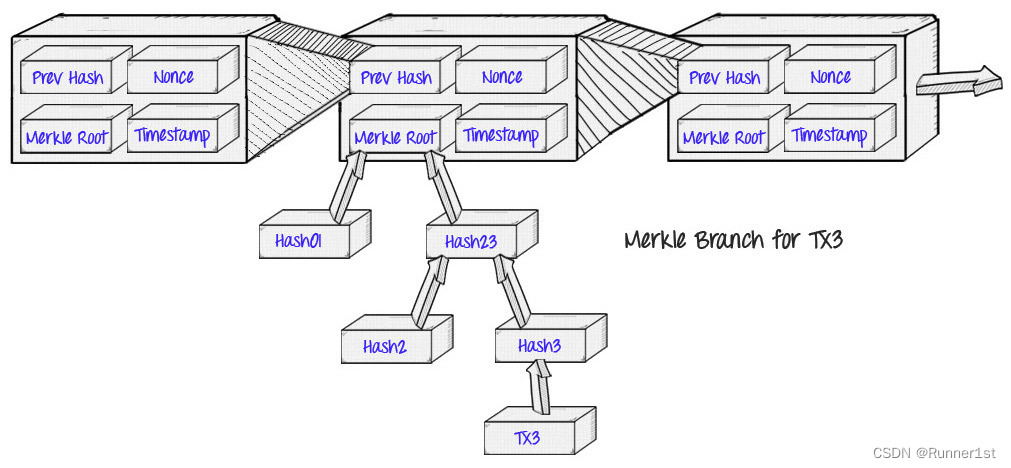
?这可以应用在“简单支付校验”(simplified payment verification)中:“轻客户端”节点无需下载区块的所有交易数据,只需要下载区块头,当需要获取一个交易的状态时,只需要向全节点请求该交易的一个默克尔证明,以证明该交易确实存在于一棵默克尔树中,并且该树的树根记录在区块头中。
1.2 Trie
Trie 是一种有序的树结构,用于存储和检索键值对(key-value),其中 key 可以映射到有限“字符集”组成的字符串,树的每个节点记录了一个字符,并且指向了下一个字符,每个路径可以组成一个完整的 key,这使得节点可以共享相同的前缀。这种数据结构可以高效地存储和检索有相同前缀的 key 集,实现简单并且占用内存小,常被用于实现路由表以及在路由器等低规格的设备中运行的系统。
“Trie” 一词提取自 “retrieval”(数据检索)的中间部分,根据其特征,也叫前缀树(Prefix Tree)、字典树等。
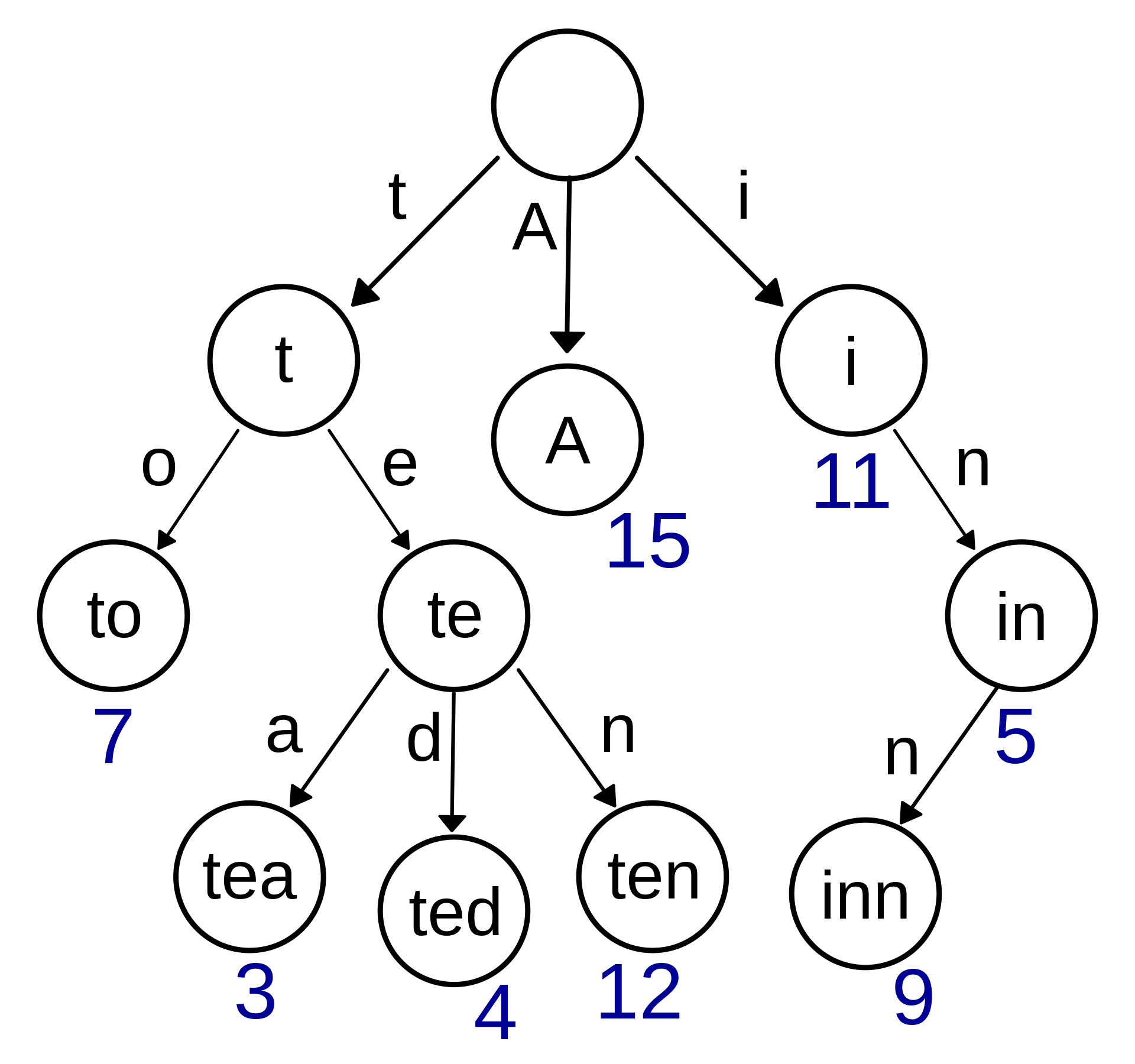
?上图表示了一棵前缀树,存储了 key 值 "A", "to", "tea", "ted", "ten", "i", "in", 和 "inn",每个 key 对应了一个数字作为 value,比如 "A" 对应的值为 15。注意图中的节点标注了完整的单词,但这只是为了演示 Trie 的原理,实际上完整的 key 并不存储在节点中,而是由路径组成的。
在一种具体实现中,Trie 的每个节点存储了一个固定长度的数组,数组的每个元素(除最后一个元素)是指向子节点的指针,数组的最后一个元素存储了 value(若存在),表示根节点到本节点的路径组成的 key 对应的 value。
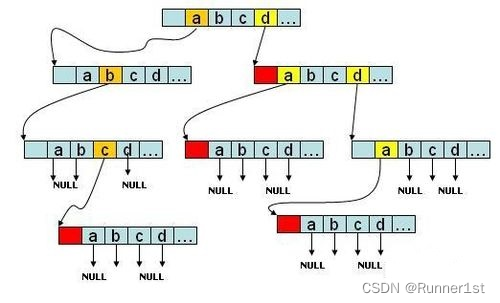
例如,一种用来存储英文单词(26个字母)的树,每个节点存储的数组长度为 27,下标 0~25 代表 a-z 字符,下标 26 代表 value。如下图所示:
 ?
?
Trie 有一个很大的缺点,即当某个 key 不与其他 key 共享前缀,并且长度很长时,会使得树极为不平衡,即高度不可控,这给攻击者提供了攻击的可能。如下图所示:
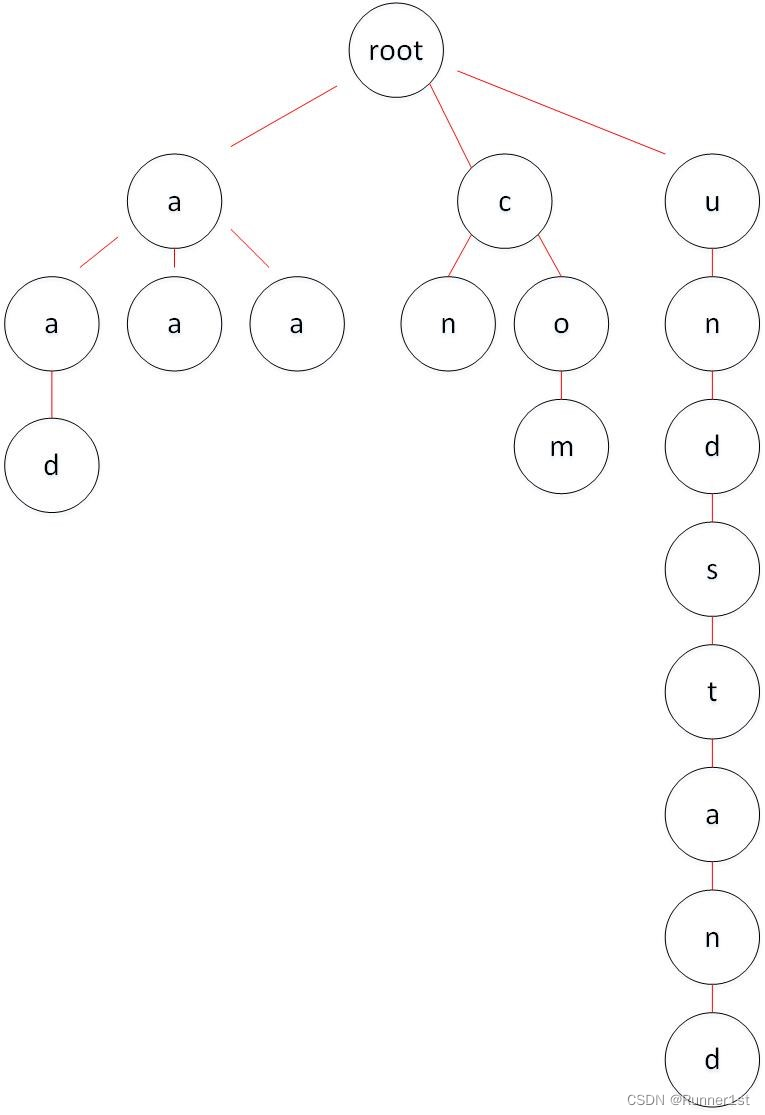
?为了解决这个问题,有新的数据结构被提出。
1.3 Patricia Trie
Patricia 一名取自论文?PATRICIA - Practical Algorithm to Retrieve Information Coded in Alphanumeric 的首字母缩写,也叫压缩前缀树、基数树(Radix Tree),是 Trie 的一种改进——当某节点只有一个子节点时,子节点与父节点进行合并。这使得压缩前缀树可以更高效地用于存储小数据集(特别是 key 长度很长时)和 相同前缀较长的数据集。
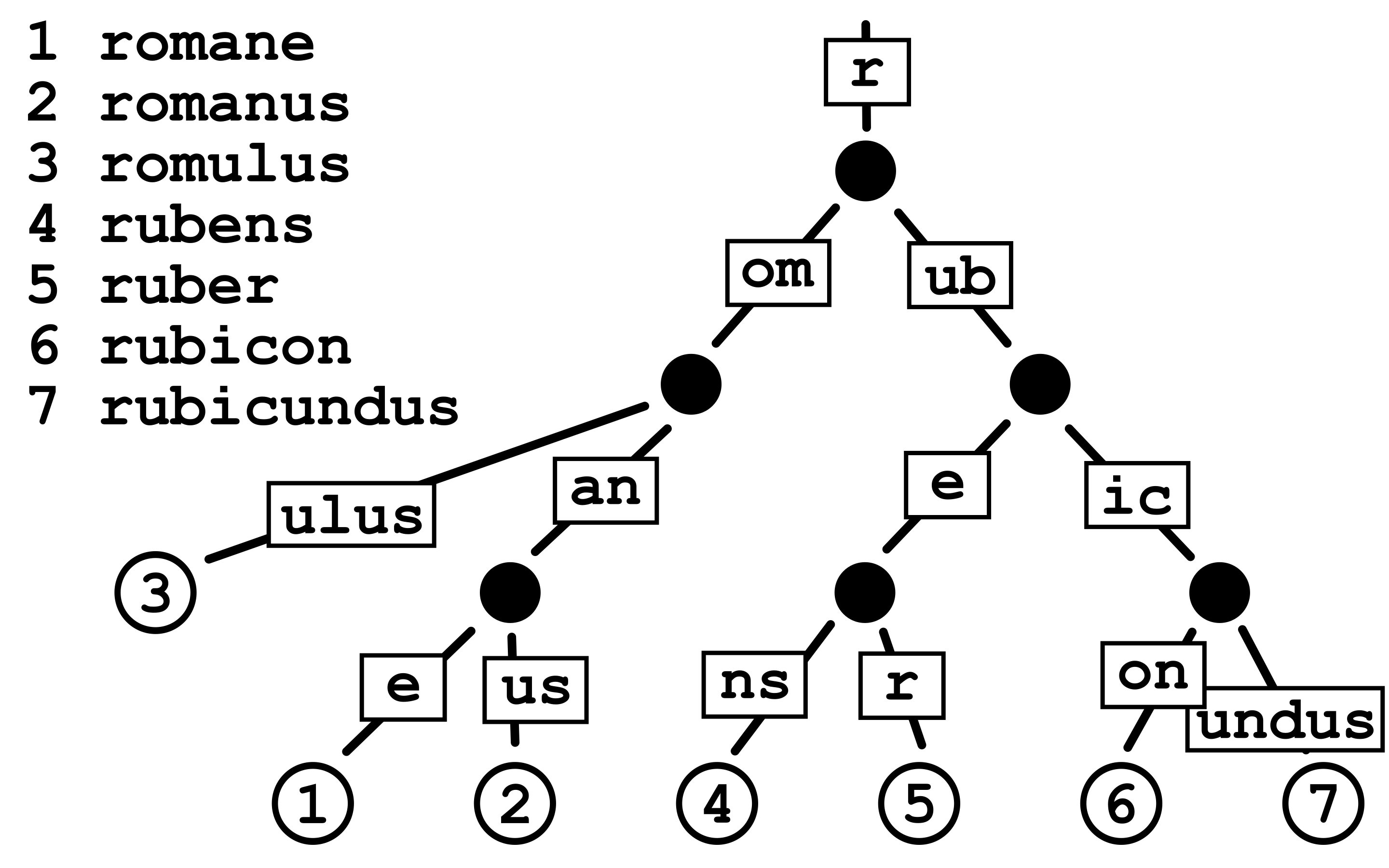
2. Merkle Patricia Trie
在了解了 Merkle tree 和 Patricia Trie 之后,我们来看看以太坊中的 MPT 树是如何把这两者结合起来,以完美地应用两种数据结构的特点。
2.1 节点类型
首先,MPT 树可以看成是压缩前缀树一种实现,为了实现压缩前缀树,MPT 树定义了如下节点类型:
- 空白节点 NULL
- 分支节点 branch [ v0 ... v15, vt ]
- 叶子节点 leaf [encodedPath, value]
- 拓展节点 extension?[encodedPath, key]
其中分支节点就是最基础的 Trie 节点,包含长度为 17 的数组(为什么是 17 下文会有解释),前 16 个元素表示十六进制字符集,最后一个元素存储该分支对应的value(如果存在);
而拓展节点就是优化后的压缩前缀树新增的节点,其中 encodedPath 表示所有被合并的节点字符组合(“部分路径”)的编码,key 指向下一个节点;
叶子节点是拓展节点的一种特殊情况,key 在该节点终止,value 为对应的值。
2.2 Key 定义
另外一个值得关注的是 MPT 树的 key,我们明确下以太坊中定义的各种 key 的概念:
- Origin Key:数据的原始 key,为字节数组。
- Secure Key:为原始 key 计算哈希 Keccak256(Origin Key) 的结果,长度固定为 32 字节,用于防止深度攻击。后文我们将看到以太坊的状态树和存储树使用这种 Key 类型。
- Hex Key:将 Origin Key 或 Secure Key 进行半字节(nibble)拆解后的 key,为 MPT 树真正存储的 key。每个 nibble 的长度为 4 bit,可以表示数字 0~15,这一步可以看成是将 key 映射到十六进制字符 0~f 组成的字符串,这就是为什么分支节点的数组长度为 17(16+1)。也就是说,在以上条件的限制下,MPT 树 key 的长度固定为 64 字符。
- HP Key:hex prefix encoding,Hex 前缀编码,当我们使用 nibble 寻找路径时,我们可能最后会剩下奇数个的 nibble,但是由于数据存储的最小单位是字节,所以可能会带来一些二义性,比如我们可能无法区分 1 或 01(都存储为1字节<01>)。因此,为了区分奇偶长度,叶子节点和拓展节点的 encodedPath 使用一个前缀作为标签,另外,这个标签也用于区分节点类型。
HP 编码规则:
| Hex字符 | bits | 节点类型 | 部分路径长度 |
| 0 | 0000 | 拓展节点 | 偶数 |
| 1 | 0001 | 拓展节点 | 奇数 |
| 2 | 0010 | 叶子节点 | 偶数 |
| 3 | 0011 | 叶子节点 | 奇数 |
另外,对于偶数路径长度的前缀(0或2),会使用半字节 0 补齐,而奇数路径长度的前缀会直接作为半字节拼接到奇数长度路径中,使其成为偶数长度。
例子:
拓展节点:
> 路径nibble值:[ 0, 1, 2, 3, 4, 5, ...] 路径长度为偶数
HP编码结果:'00 01 23 45'(前缀为'00')
> [ 1, 2, 3, 4, 5, ...] 路径长度为奇数
'11 23 45'(前缀为'1')
叶子节点:
> [ 0, f, 1, c, b, 8, 10] 路径长度为偶数(注:最后一个10为值)
'20 0f 1c b8'(前缀为'20')
> [ f, 1, c, b, 8, 10] 路径长度为奇数
'3f 1c b8'(前缀为'3')
再以一个简化的以太坊世界状态树作为例子:
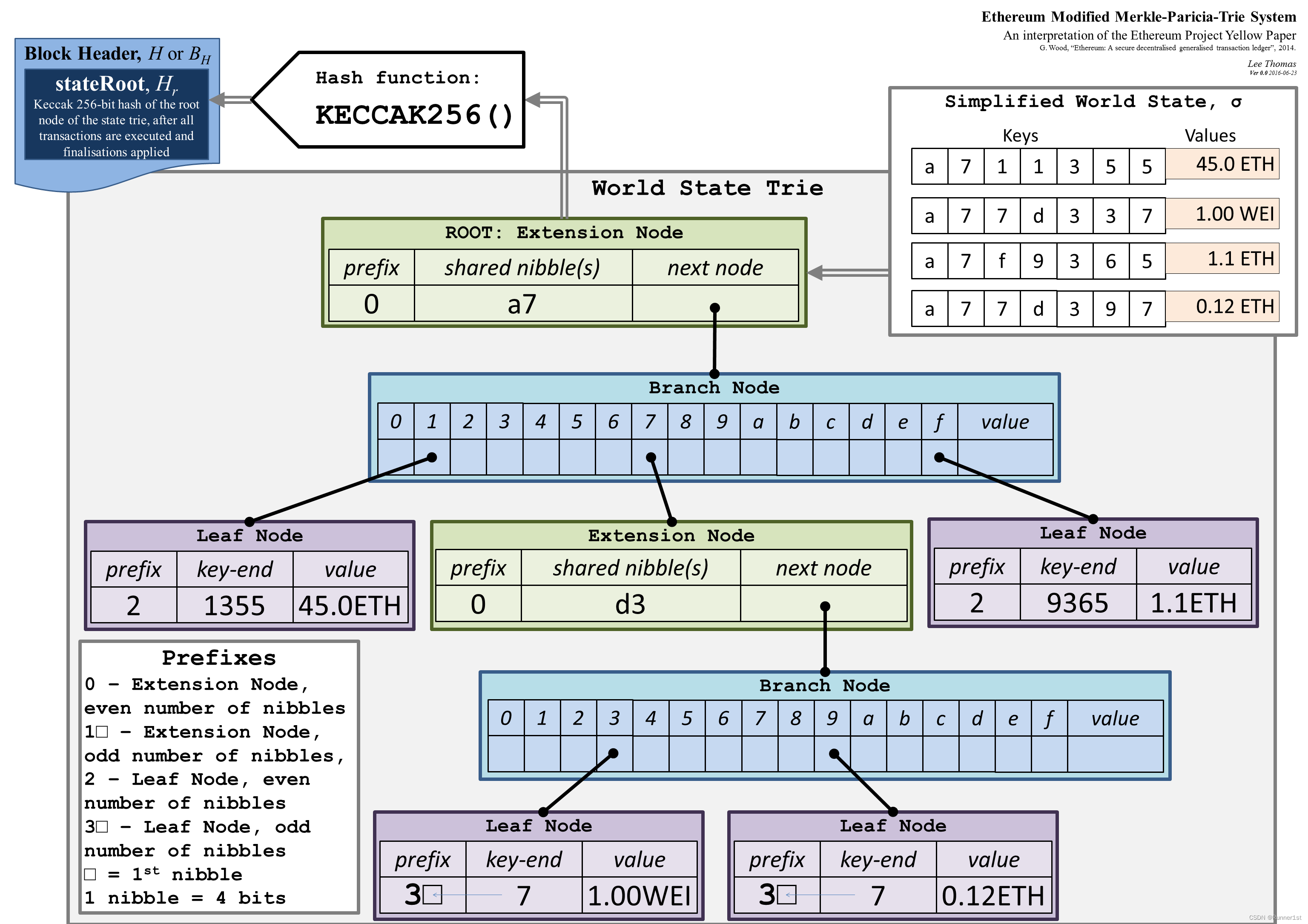
右上角为简化的 key-value 定义。我们可以看到图中有 2 个拓展节点,2 个分支节点,4 个叶子节点。在最下面的两个叶子节点中,prefix 3 的右边有个格子,有个箭头从 7 指向这个格子,表示 3 和 7 两个 nibble 组成一个字节存储,与我们上面的编码规则是一致的。
2.3 节点哈希
以上我们讲的都是“压缩前缀树”的特点,那 MPT 树的“默克尔”部分体现在哪里呢?
实际上,当一个节点被另一个节点在内部指向时(比如上图中的分支节点内部指向了叶子节点),父节点会存储H(rlp.encode(x)),其中?H(y) = keccak256(y) if len(y) >= 32 else y,?rlp.encode?为 RLP 编码函数。即当子节点内容的 RLP 编码结果小于 32 字节时,则直接存储在父节点中,否则,则存储编码结果的哈希值。对于后者,如果需要根据哈希读取出子节点的内容,还需要在数据库中存储?keccak256(y)?到?y?的映射;而对于前者,子节点的内容直接记录在父节点中,所以子节点无需再单独存储,这可以减少磁盘 IO 次数。
这个特性使得父节点的哈希值计算依赖了子节点,也就让 MPT 树具备了“默克尔”的性质。
3. 以太坊“四棵树”
以太坊(执行层)中的所有默克尔树都使用了 MPT 数据结构。
网上的大多数文章,一般都是说以太坊有“三棵树”,这是因为以太坊的区块头中存储了以下三个树根:
- transactionsRoot?交易根
- receiptsRoot?回执根
- stateRoot 状态根
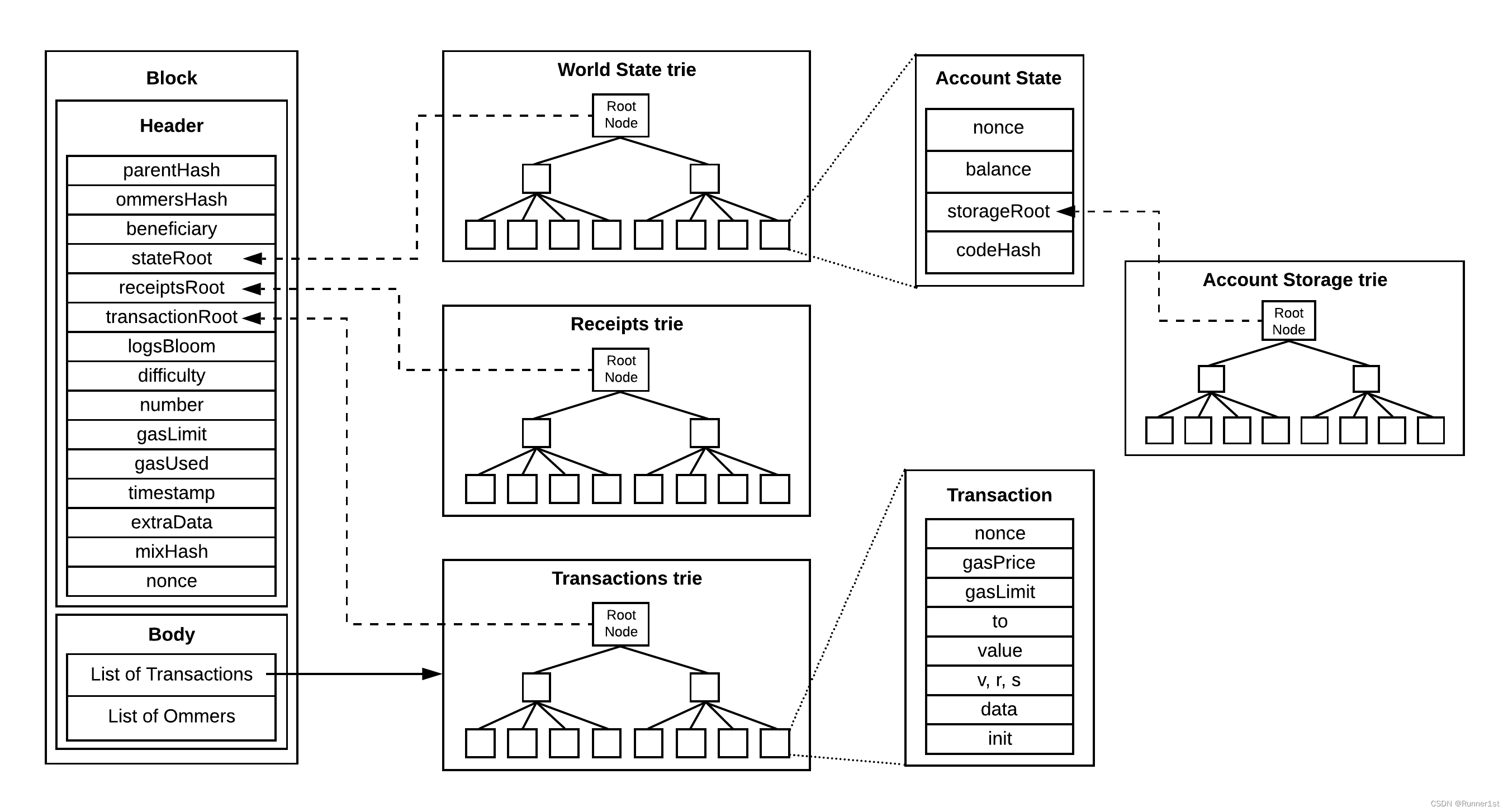
?从上图中我们可以看到,除了区块头中三个树根对应的三棵树之外,还有第四棵树——存储树。
下面我们分别来看这四棵树的构成。
3.1 交易树
每个区块都有一棵独立的交易树,对应区块头里的交易根。交易树的 key(路径)为?rlp(transactionIndex),value 为交易序列化后的值。其中?transactionIndex?表示交易在该区块中的下标。
对于交易序列化的细节,可参考 EIP 2718。
3.2 回执树
每个交易对应一个交易回执,交易回执记录了交易执行结果,包括执行状态、Gas消耗、事件日志等。每个区块也有自己的回执树,对应了区块头里的回执根。与交易树类似,key 为?rlp(transactionIndex),value 为交易回执序列化后的值。
对于交易回执序列化的细节,可参考 EIP 2718。
3.3 状态树
状态树要稍微复杂一些。与交易树和回执树不同的是,状态树是全局的、不断更新的。它的 key 为 keccak256(ethereumAddress),value 为 rlp(ethereumAccount)。其中?ethereumAddress?表示以太坊账户地址;?ethereumAccount?表示以太坊账户,包含四个字段 [nonce,balance,storageRoot,codeHash]。
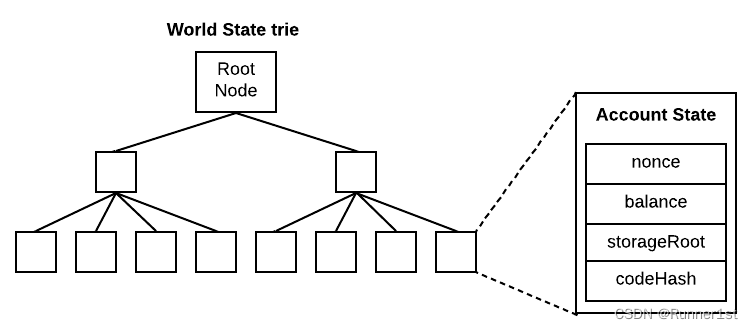
?以太坊有两种账户,分别是 EOA(Externally-Owned Account,外部拥有账户)和 合约账户,对于两种账户的介绍和区别可以参考 Ethereum Accounts。 简单来说,如果?storageRoot?和?codeHash?不为空,则为合约账户,其中 codeHash? 对应合约代码的哈希,storageRoot?对应另一棵树的树根,这棵树我们称为存储树。
3.4 存储树
这就是我们说的第四棵树。虽然每棵存储树的树根都存储在状态树中,但是存储树跟状态树的 key 和 value 都不同,所以它值得有自己的名字。
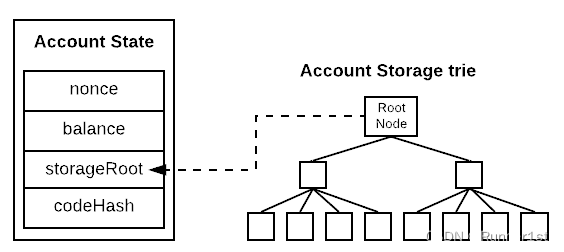
?存储树存储了合约的所有状态数据,每个合约有单独的存储树。它的 key 为?keccak256(position)?,value 为?position?对应值(32字节)的 rlp 编码。其中 position 为状态变量在合约中存储槽的位置,用32字节表示,比如以下合约代码定义的第一个 uint256 变量 a,存储槽为 0,那么key为?keccak256(0x00000000000000000000000000000000)?。
contract StorageTest {
uint256 a;
// ......
}当然,对于动态长度数组和 Map 等较复杂类型的变量,position 计算会稍微复杂一些,具体计算方法可参考 Understanding Ethereum Smart Contract Storage。
一个有意思的事实是,由于 MPT 树是确定性的,所以如果两棵树存储了完全相同的数据,那么这两棵树的节点将完全相同,包括根节点。因此,如果两个相同的合约,存储的数据刚好完全相同,那么在状态树中它们的?storageRoot?是相等的,即对应了同一棵存储树。通过上面 MPT 树的讨论,我们知道,节点在硬盘中是以(节点哈希,节点内容)这样的键值对存储的,所以当两个合约的存储树相同时,实际上他们共享了相同的硬盘数据。那么可能会带来这样的疑惑:这两个节点在读写数据时不会冲突吗?自然是不会的。假设在某一时刻,当其中一个合约修改了某个变量的数据,使得它与另一个合约的数据不同时,会生成一个新的节点,并从新节点开始由下往上直到根节点,整个路径的节点值都会更新,新生成的节点会存储到硬盘,但旧的节点不会从硬盘删除。
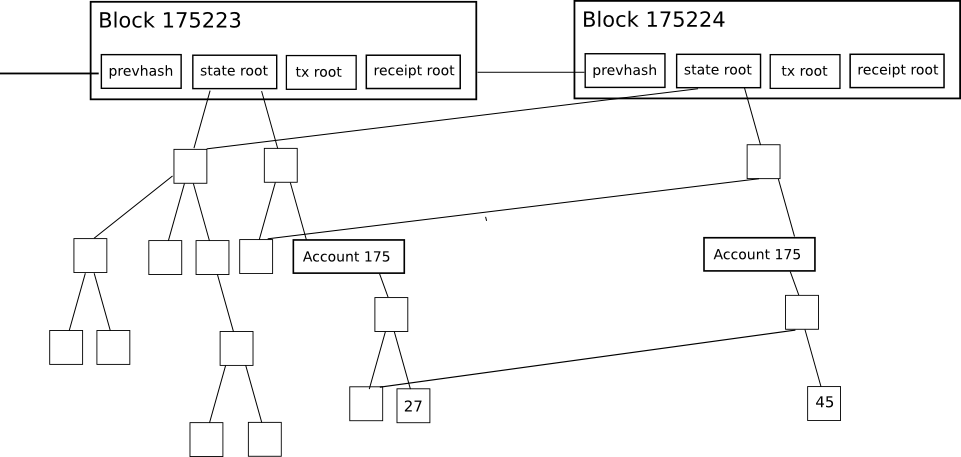
?以上图为例,左边是区块 175223 的状态树和存储树,其中账户 175 有个变量的值为 27,假如在区块 175224 中,有一个交易的合约调用将该变量的值改为 45,那么该值所在节点的哈希会变化,从该节点到存储树根节点整个路径的节点内容和哈希也随着变化,账户 175 在状态树中的?storageRoot?也会被更新,最终影响到状态根的变化。所有受影响的节点都会作为新节点存储,而其他节点仍然维持不变,这就形成了上图中不同区块对应的状态树共享一部分数据的情形。这样做的好处是显而易见的,所有历史数据都不会删除,只要拿到区块头中的状态根,就能定位到执行到该区块为止的状态数据。
因此,当我们调用以太坊的?eth_getStorageAt 接口读取状态数据时,我们需要提供合约地址、存储槽位置(position)、区块ID。根据区块ID,可以定位到区块头的状态根哈希,根据状态根哈希,从硬盘中读取状态根节点,再根据状态根节点中的子节点哈希,根据需要依次从硬盘读取其他节点,从而获取到了状态树;根据合约地址,可以从状态树中定位到合约账户信息,从中读取?storageRoot?,从而定位到存储树;最后,我们根据存储槽位置从存储树中读取出状态数据。
比如,我们读取合约地址?0x295a70b2de5e3953354a6a8344e616ed314d7251?的存储槽 0 的最新区块下的状态数据,请求和响应如下:
curl -X POST --data '{"jsonrpc":"2.0", "method": "eth_getStorageAt", "params": ["0x295a70b2de5e3953354a6a8344e616ed314d7251", "0x0", "latest"], "id": 1}' localhost:8545
{"jsonrpc":"2.0","id":1,"result":"0x00000000000000000000000000000000000000000000000000000000000004d2"}相关阅读
- 维基百科:Merkle Tree
- 维基百科:Trie
- 维基百科:Radix Tree
- Merkling in Ethereum
- Morrison, Donald R. PATRICIA -- Practical Algorithm to Retrieve Information Coded in Alphanumeric
- 以太坊官网:RLP 编码
- 以太坊官网:Patricia Merkle Trees
- 以太坊官网:Ethereum Accounts
- 以太坊智能合约存储槽详解:Understanding Ethereum Smart Contract Storage
- 详解以太坊默克尔压缩前缀树-MPT
- Merkle Tree and Ethereum Objects - Ethereum Yellow Paper Walkthrough (2/7)
- Github: go-ethereum Trie 源码