博客是以技术探讨为目的,不构成任何投资建议
炒币有风险,投资需谨慎
请遵守相关法律法规
一、hash pointer
即:hash指针,与普通指针的区别在于hash指针不仅保存数据在内存中的位置也保存数据的hash值,记作:H()

对于我们常说的区块链本质上就是由一个个区块组成的链表,它与传统链表的区别首先就是使用hash指针代替普通指针,即:block chain is a linked list using hash pointers,下面是一个区块链的示意图
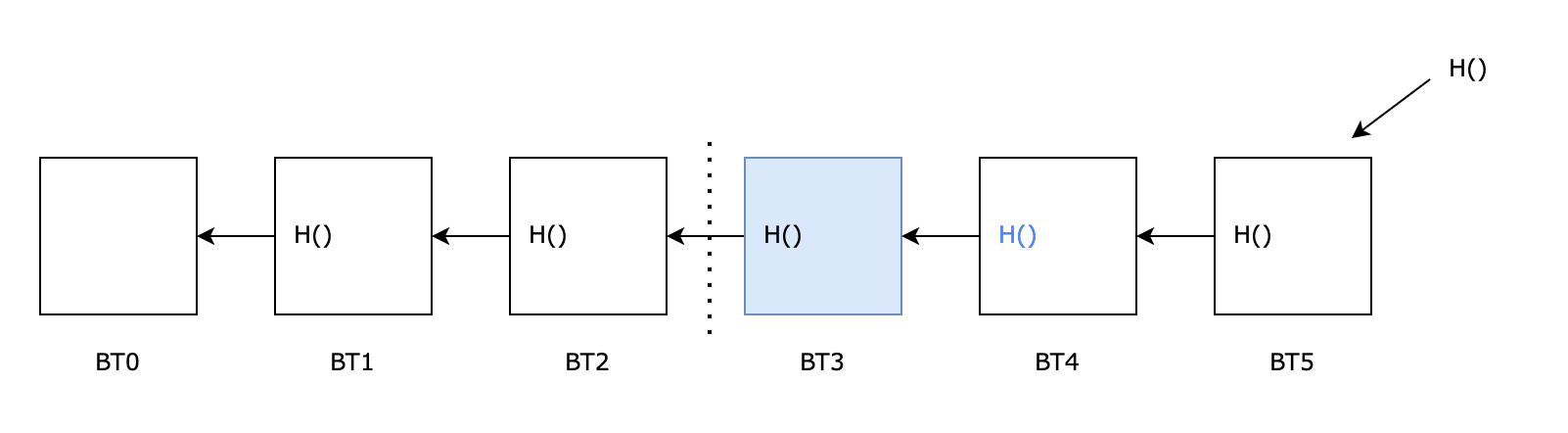
BT0为系统初始化创建的第一个区块称为:genesis block(创世纪块),之后的每一个区块都包含指向前一个区块的H()
注:取H()时是将前一个区块的整个内容包括它的H()合在一起取hash,例如BT4的H()是将BT3区块内容加上BT3的H()合在一起求hash值
这样的数据结构有一个好处,可以做到tamper-evident log(即防篡改),例如:假设BT3的内容被篡改了,为了链的完整性同样需要修改BT4的H(),同理修改BT5的H(),最终修改保存在系统中指向最后一个区块的H(),而指向最后一个区块的H()是所有用户保存在本地,因此这样的数据结构可以仅凭一个H()就可以检验对链上任意位置的修改,这就是区块链和普通链表的区别。
有了这个性质区块链上的某些节点就可以不比存储整个区块的数据了,例如只保存近1000个区块的数据。如果需要使用历史区块则可以向链上其他节点请求,但区块链上的某些节点可能是有恶意的,如何确保其他节点给的区块是否正确?例如
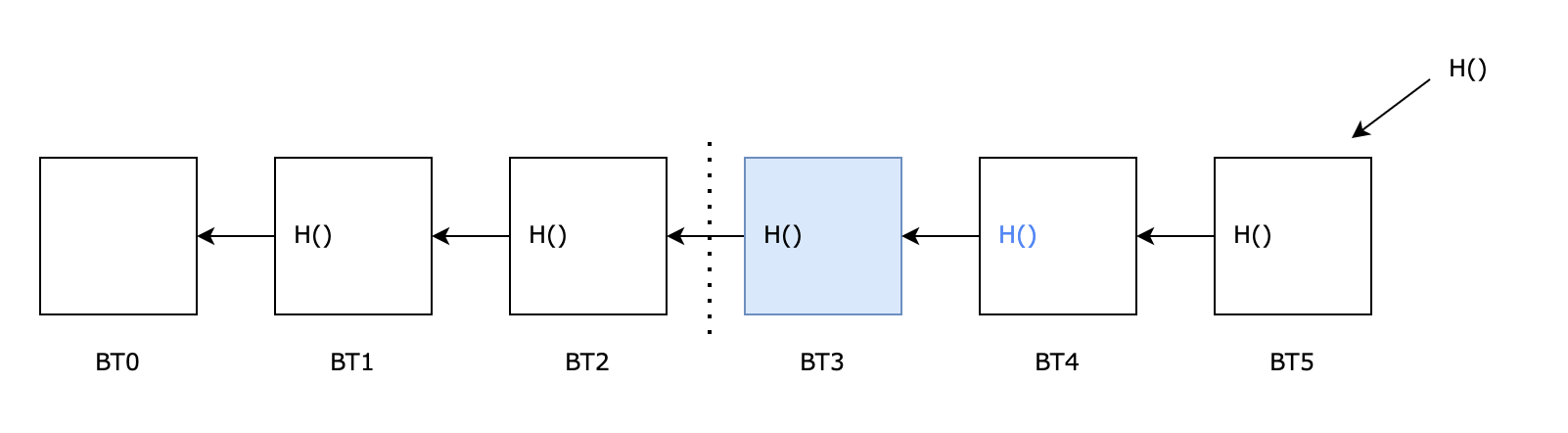
某个节点只保存到BT3的区块,对于从其他请求过来的BT2区块只需要计算一下BT2的hash与BT3保存的H()是否一致即可知道BT2的数据有没有被篡改
二、merkle tree
与区块链的结构类似,merkle tree与普通数的区别在于使用hash pointer代替普通指针,下面是merkle tree的简单视图
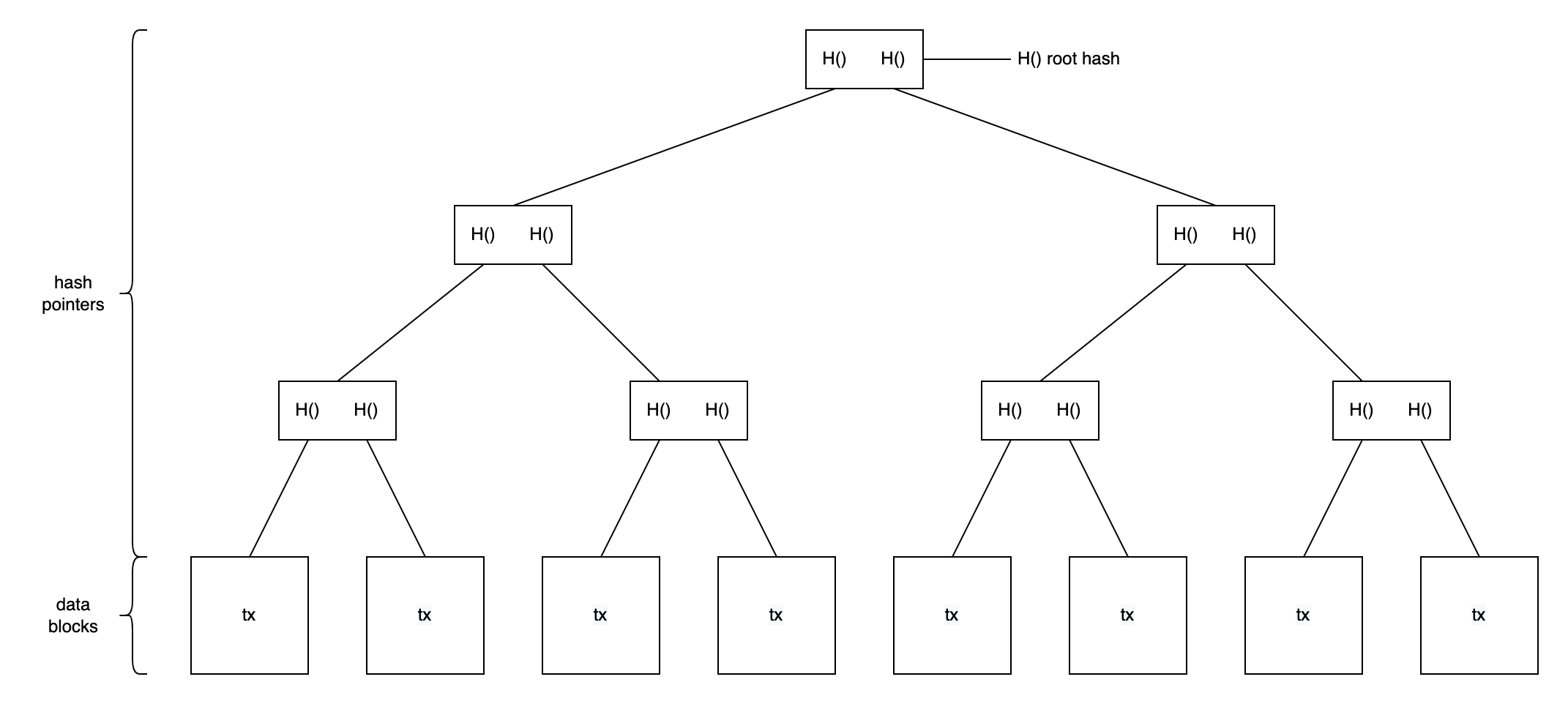
其叶子节点称为data block(数据块),每个data block的H()存储在上一个节点中,H()与H()再计算一个H()存储到上一个节点中,以此类推最终可以得到一个树形结构,顶层的H()称为root hash。这样的好处是只需要记录一个root hash就可以保护整个树,只要叶子节点的任意位置发生了修改与之相关的H()都会发生变化,最终导致root hash发生变化,且时间复杂度为O(logn)。如果只引用在数据防篡改上,例如P2P的下载,merkle tree的效率是要比hash list快许多的
三、merkle tree与区块链
上述两种数据结构在区块链中是怎么运用的?
在比特币中,区块与区块之间使用hash pointer连接,每个区块所包含的交易组织成merkle tree;同时每个区块分为block header(块头)和block body(块身),其中block header存储
- 上一个区块块头的hash
- 时间戳
- 挖矿难度值,即上一章说的target
- 工作量证明随机数(nonce)
- merkle tree的root hash
block body存储所有的交易信息组成的merkle tree,因此比特币中完整的数据结构如下
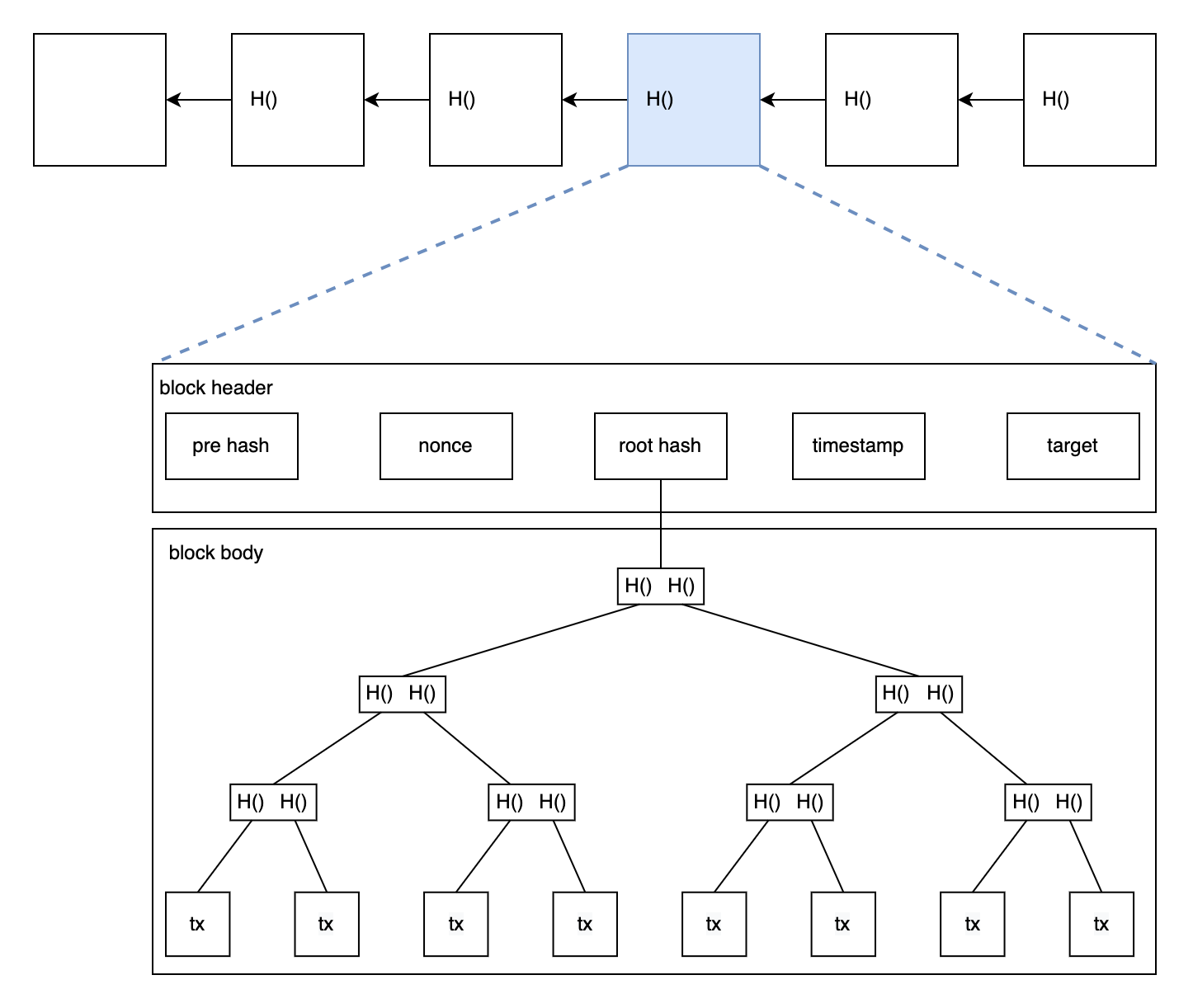
注:block header没有交易信息,只保存root hash,交易信息只存储在block body
merkle tree最大的用处就是提供merkle proof
3.1 merkle proof
比特币系统中节点分为全节点和轻节点,全节点保存整个区块的内容(block header+block body)而轻节点只保存block header,例如手机端的比特币钱包就是轻节点。那么就存在一个问题:如何向一个轻节点证明本次交易已经被写入区块链?
因此中本聪提出SPV(简化支付验证),即使用merkle proof
首先找到本次交易的data block,从这个区块往上一直到根节点的路径就被成为merkle proof,即淡蓝色标记
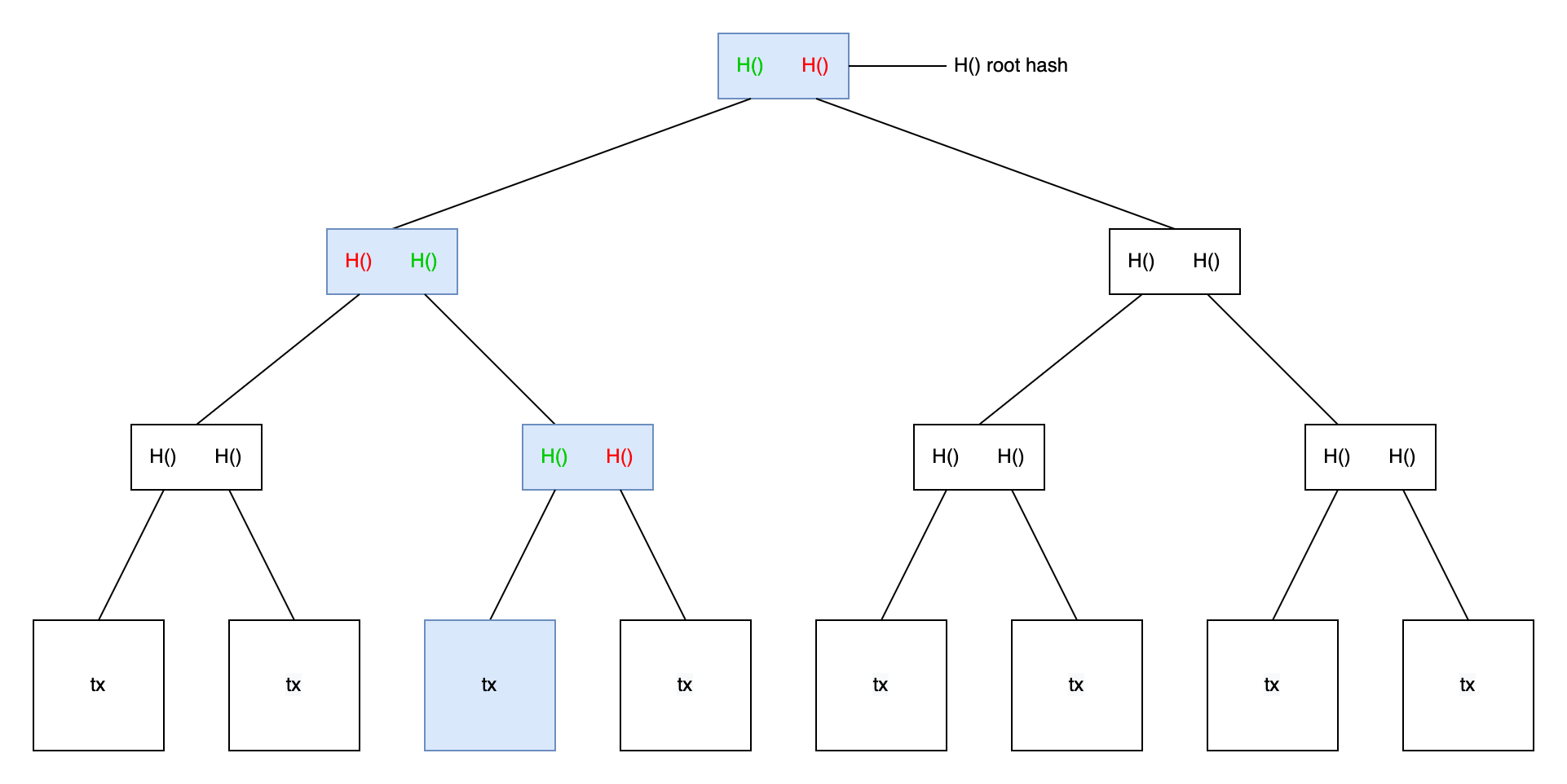
那么轻节点如何验证验证本次交易呢,此时轻节点向某个全节点发起请求获取本次交易的merkle proof,全节点返回上图中标红的hash值;轻节点首先在本地计算此次交易所在的data block的hash值,即标绿的hash值,与全节点返回的hash值组合在一次计算上一层标绿的hash值,直到算出root hash与轻节点保存的root hash比较即可验证。因此又被称为proof of membership(proof of inclusion)
注:merkle proof 只能验证自己所在路径的hash,即只能验证上图标绿的hash
如何高效证明交易不存在merkle tree中
上述merkle proof方式可以以对数级别的复杂度证明交易存在这个merkle tree中,那么如何证明不存在。一个简单的方法就是把整个merkle tree传给轻节点挨个遍历,此时的时间复杂度为O(n),如果不对merkle tree的叶子结点做任何约束那么这就是最高效的方法。
如果叶子节点按照hash值进行排序,则可以实现对数复杂度的证明,此时被称为sorted merkle tree,但比特币中没有使用这种数据结构,因为比特币中不需要做不存在证明。