首先给出比赛 Link
一:异常值、空值的处理
训练集中RESOURCE/DISK_USAGE字段在靠前部分存在大量空值。通过可视化可知,该部分采样时间间隔与后面明显不一致,且CPU使用率均为0。猜测该部分空值对应的时间为系统初始化状态,因此判断导致数据缺失的可能原因是服务器尚未开始启动,可以直接进行删除而不造成正常工作状态信息丢失。

通过可视化可知,两个任务目标的训练集测试集分布存在明显差异(为了方便观察使用了kde进行拟合),特别是JOB在训练集和测试集中分布差异极大,训练集中最大值为140测试集则为200。后期直接采用规则预测的方式给出JOB的预测值,设定预测值直接等于最后一刻的LAUCHING_JOB_NUMS(比直接建模高0.01左右),CPU占用率则使用常规建模的方法进行预测。
- 此外CPU_USAGE/MEM_USAGE等呈长尾分布,进行目标变换(这里使用开根号)使得序列更加平稳。
 ?
?
?由于训练集中某些特征存在测试集中不包含的离散值 根据此进行筛选,在训练集中去掉含有这些取值的样本。
- 根据时间进行排序,并去重复时间对应的样本。
- 对训练集进行重新分组,首先根据qid分组,然后根据时间间隔,若相邻样本(由于之前已根据时间进行排序),时间间隔大于30(题目要求的预测未来时间是5-25,这里比较随意的给定了一个30) ,则将其分为另外一组(这一步操作与之后特征处理以及目标值构造时的操作有关)(只考虑到了相邻的样本的时间),简而言之:根据时间差不同,将样本划分成若干组。
?二:特征工程
交叉特征
- CU与CPU_USAGE相乘,CU与MEM_USAGE相乘,将资源的百分比占用量转换为实际占用资源量。
- MEMS_USAGE与DISK_USAGE相加,表征存储资源总占用。
- 多种任务数量特征与CU相除,表征单位资源上的任务数量。

时序特征
- 时间点,小时(分钟)---构建小时(分钟)特征,根据前面的作图我发现一天当中的不同时段CPU的使用率分布还是有很大区别的,所以加入了 (hour*60+min)的时间特征。事实证明这个提分非常大,几个百分点的提分,在前期让我直接坐上榜二的位置。
- 历史值,X2,X3……,通过热力图(相关性分析)分析,可以明显看出当前时间点的CPU使用率与临近时间点的CPU使用率具有强相关性。
- 一阶差分,X1-X2, X3-X2……、当前与之前四个点的差分特征
- 窗内均值,mean(X1, X2), mean(X1, X2, X3)……
- 不同窗均值比,mean(X1, X2)/mean(X1, X2, X3)……
- 单点趋势值,X1/mean(X1,X2,X3,X4,X5)……
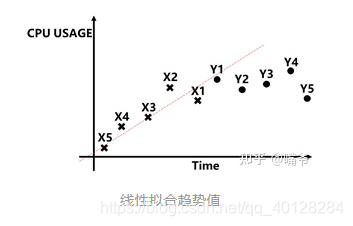
- 线性拟合趋势值,5点线性拟合斜率K
- 含有物理信息特征:正在等待执行的作业数减去运行中的作业数 , 正在等待执行的作业数除以队列规格,?运行中的作业数除以队列规格,CPU使用率除以内存使用率,取消的作业数加上失败作业数。
相关性分析:可以用DataFrame中corr()方法来进行分析:
DataFrame.corr(method: {'pearson', 'kendall', 'spearman'})
相关方法:
- pearson:标准相关系数------------度量两变量x和y之间的线性关系,为spearman相关系数的一种特殊情况。
- kendall:Kendall Tau相关系数-----------表示等级变量相关程度的一种方法,不常用。
- spearman:在线性关系不显著时,我们考虑采用Spearman秩相关系数------------相关系数表明X(独立变量)和Y(依赖变量)的相关方向。如果当X增加时,Y趋向于增加,斯皮尔曼相关系数则为正。如果当X增加时,Y趋向于减少,斯皮尔曼相关系数则为负。斯皮尔曼相关系数为零表明当X增加时Y没有任何趋向性。当X和Y越来越接近完全的单调相关时,斯皮尔曼相关系数会在绝对值上增加。当X和Y完全单调相关时,斯皮尔曼相关系数的绝对值为1。
在时序问题中,通常获取历史特征之后,我们就可以求取其均值、方差、最大值、最小值和中位数等特征,用以刻画一段时间内的数据分布,从而帮助我们的模型去学习。
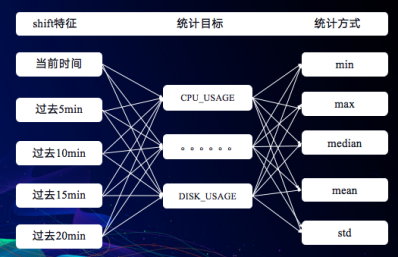
聚合特征
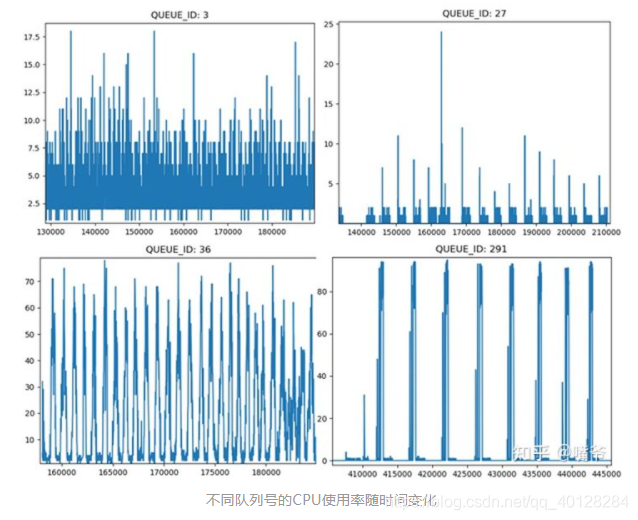
不同队列的状态变化存在显著区别,同时随时间呈一定周期性变化。为了提取该信息,将时间戳转换为一天内的小时信息,同时根据队列名及小时进行聚合。为了从多角度对分布进行刻画,采用了多种统计值,包括:最大值,最小值,均值,中位数等。
三:建模
- 嘴爷采用:在lgb中对5个未来时间点分别建模,lstm则可同时预测5个时间点值。我在lgb建模时采用迭代预测的方法,将前一个时间点的预测值作为特征输入下一个时间点。迭代预测同时可能存在一个问题,后面的预测会受到前一个点预测误差影响。
siguo采用:输入前5个样本,预测后5个样本,预测的目标变化为预测当前与未来的差值。
四:特征筛选
为了更进一步上分,在十折交叉验证中,加入RFE递归特征消除做特征筛选,使用LGB模型作为筛选方式,保留若干个特征。
from sklearn.feature_selection import RFE
rfe = RFE(estimator=LGBMRegressor(), n_features_to_select=30)
rfe_train = pd.DataFrame(rfe.fit_transform(df_train, targets[i]))
rfe_test = pd.DataFrame(rfe.transform(df_test))五:后处理
通过验证集可视化可以发现,模型的预测结果明显偏小,乘以系数可以显著提高分数。
- 因为测试集的分布和训练集不一致,测试集的CPU使用率偏高一点,所以我给结果整体加/乘上了一个小常数 ,使它更好的拟合测试集,感觉这其实是玄学做法,但是有几个千分点的提分。

Tips
- 有高分队伍对每个队列分别进行建模,这样可以减少不同队列之间的干扰,但可能丢失所有队列的共性特点,也会降低每个模型的训练数据。
- 长尾分布可以采用开根号、取对数等方式使得序列平稳,也可以考虑差分。
- JOB预测可以考虑目标变换后建模,而非直接规则预测。【忘记之前有没有尝试了。。。
- 在lstm模型中对队列号尝试了多种编码,例如根据训练集qid对应的CPU均值、标准差进行编码,有些好有些差,可以多多尝试。
- lgb中将队列号置为category属性,有一定提升。
- 由于训练集中采样间隔不同,最好能进行处理,我做了一些尝试并不理想。
- 同6,尝试对时间进行重采样,线性填充
- 尝试将CPU*CU/100,即cpu_use作为预测的目标值,最后将结果变换回去
- 尝试先进行分类预测目标值未来趋势,将分类值或概率作为特征加入数据中(二分类(提升、下降)或三分类(提升、平稳、下降))
Tricks:
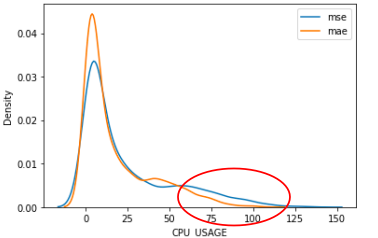
- 第一个是修改了预测目标,用差分值代替原始目标,此想法基于邻近时间的几个点通常具有较强的相关性,而事实数据也证明差分后要比差分前在0点处的密度提升很多。
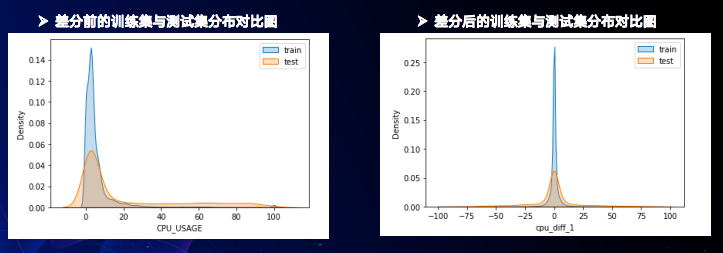
- 而第二个则改进是修改了损失函数,比赛方在评价我们成绩好坏的时候使用的是MAE损失函数,但我们通过数据探索分析发现,训练集和测试集出现明显的分布不一致的问题,这会导致测试集中不一致的部分会被认为是“异常值”,而MAE对“异常值”不敏感的特点使得在预测过程中,这一部分的数据会变得不准确,因此我们修改损失函数将MAE改成MSE提高模型对于“异常值”的敏感性来保证在实际预测中,对这一部分数据的预测更具鲁棒性。