我们换一种方式,申请一个bit数组,数组大小为4294967295,大概为40亿bit,40亿/8 = 5亿字节,那么需要0.5G空间, bit数组的每个位置有两种状态0和1,那么怎么使用这个bit数组呢?呵呵,数组的长度刚好满足我们整数的个数范围,那么数组的每个下标值对应4294967295中的一个数,逐个遍历40亿个无符号数,例如,遇到20,则bitArray[20] = 1;遇到666,则bitArray[666] = 1,遍历完所有的数,将数组相应位置变为1。
4、40亿个非负整数中找到一个没有出现的数,内存限制10MB
? 本题将内存空间缩小为10MB,对于40亿个数据来说那是明显不够用的,那么我们只有将数据分块处理,分块应该怎么分,分多少块合理呢?根据我做过的题经验来看,10亿个字节的数据大概需要1GB空间处理(如果这个结论不正确欢迎读者指出),那么10MB内存换算过来就是可以处理1千万字节的数据,也就是8千万bit,对于40亿非负整数如果申请bit数组的话,40亿bit / 0.8亿bit = 50,那么这样最少也得分50块来处理,处理每块数据的时候几乎用完了内存空间,这样也不太好。看书上解说是分成了64块,至于为什么是64我目前也不是很了解,我只知道最少50块。所以下面就以64块来进行分析解答吧。
首先,将0 - 4294967259这个范围平均分成64个区间,每个区间是67108864个数,为了定位更加准确一些,我们先开辟一个大小为64的整型数组intArray,将40亿个数进行区间划分,第0区间(0-67108863)、第一区间(67108864-134217728)、第i区间(67108864i-67108864(i+1)-1),…,第63区间(4227858432 - 4294967259)。intArray分别记录每个区间出现的数的个数,肯定至少有一个区间上的计数少于67108864.利用这一点可以快速找出一个没有出现过的数。
? 第一次遍历时,先申请长度为64的整型数组countArr[0…63],countArr[i]用来统计区间i 上的数有多少。遍历40亿个数,根据当前数是多少来决定哪一个区间上的计数增加。例如,如果当前数是3422552090,3422552090/67108864=51,所以第51区间上的计数增加countArr[51]++。遍历完40亿个数之后,遍历countArr,必然会有某一个位置上的值(countArr[i])小于67108864,表示第i 区间上至少有一个数没出现过。我们肯定会至少找到一个这样的区间。此时使用的内存就是countArr的大小(64×4B),是非常小的。
假设我们找到第37区间上的计数小于67108864,以下为第二次遍历的过程:
1.申请长度为67108864的bit map,这占用大约8MB的空间,记为bitArr[0…67108863];
2.再遍历一次40亿个数,此时的遍历只关注落在第37区间上的数,记为num(num/67108864==37),其他区间的数全部忽略。
3.如果步骤2的num在第37区间上,将bitArr[num - 67108864*37]的值设置为1,也就是只做第37区间上的数的bitArr映射。
4.遍历完40亿个数之后,在bitArr上必然存在没被设置成1的位置,假设第i 个位置上的值没设置成1,那么67108864×37+i 这个数就是一个没出现过的数。
总结一下进阶的解法:
1.根据10MB的内存限制,确定统计区间的大小,就是第二次遍历时的bitArr大小。
2.利用区间计数的方式,找到那个计数不足的区间,这个区间上肯定有没出现的数。
3.对这个区间上的数做bit map映射,再遍历bit map,找到一个没出现的数即可。
5、找到100亿个URL中重复的URL
? 原问题的解法使用解决大数据问题的一种常规方法:把大文件通过哈希函数分配到机器,或者通过哈希函数把大文件拆成小文件。一直进行这种划分,直到划分的结果满足资源限制的要求。首先,你要向面试官询问在资源上的限制有哪些,包括内存、计算时间等要求。在明确了限制要求之后,可以将每条URL通过哈希函数分配到若干机器或者拆分成若干小文件,这里的“若干”由具体的资源限制来计算出精确的数量。
? 例如,将100亿字节的大文件通过哈希函数分配到100台机器上,然后每一台机器分别统计分给自己的URL中是否有重复的URL,**同时哈希函数的性质决定了同一条URL不可能分给不同的机器;**或者在单机上将大文件通过哈希函数拆成1000个小文件,对每一个小文件再利用哈希表遍历,找出重复的URL;或者在分给机器或拆完文件之后,进行排序,排序过后再看是否有重复的URL出现。总之,牢记一点,很多大数据问题都离不开分流,要么是哈希函数把大文件的内容分配给不同的机器,要么是哈希函数把大文件拆成小文件,然后处理每一个小数量的集合。
6、海量搜索词汇,找到最热TOP100词汇的方法
? 最开始还是用哈希分流的思路来处理,把包含百亿数据量的词汇文件分流到不同的机器上,具体多少台机器由面试官规定或者由更多的限制来决定。对每一台机器来说,如果分到的数据量依然很大,比如,内存不够或其他问题,可以再用哈希函数把每台机器的分流文件拆成更小的文件处理。
? 处理每一个小文件的时候,哈希表统计每种词及其词频,哈希表记录建立完成后,再遍历哈希表,遍历哈希表的过程中使用大小为100的小根堆来选出每一个小文件的top 100(整体未排序的top 100)。每一个小文件都有自己词频的小根堆(整体未排序的top 100),将小根堆里的词按照词频排序,就得到了每个小文件的排序后top 100。然后把各个小文件排序后的top 100进行外排序或者继续利用小根堆,就可以选出每台机器上的top 100。不同机器之间的top100再进行外排序或者继续利用小根堆,最终求出整个百亿数据量中的top 100。对于top K 的问题,除哈希函数分流和用哈希表做词频统计之外,还经常用堆结构和外排序的手段进行处理。
7、40亿个无符号整数,1GB内存,找到所有出现两次的数
? 对于原问题,可以用bit map的方式来表示数出现的情况。具体地说,是申请一个长度为4294967295×2的bit类型的数组bitArr,用2个位置表示一个数出现的词频,1B占用8个bit,所以长度为4294967295×2的bit类型的数组占用1GB空间。怎么使用这个bitArr数组呢?遍历这40亿个无符号数,如果初次遇到num,就把bitArr[num2 + 1]和bitArr[num2]设置为01,如果第二次遇到num,就把bitArr[num2+1]和bitArr[num2]设置为10,如果第三次遇到num,就把bitArr[num2+1]和bitArr[num2]设置为11。以后再遇到num,发现此时bitArr[num2+1]和bitArr[num2]已经被设置为11,就不再做任何设置。遍历完成后,再依次遍历bitArr,如果发现bitArr[i2+1]和bitArr[i2]设置为10,那么i 就是出现了两次的数。
8、10MB内存,找到40亿整数的中位数
①内存够:内存够还慌什么啊,直接把100亿个全部排序了,你用冒泡都可以…然后找到中间那个就可以了。但是你以为面试官会给你内存??
②内存不够:题目说是整数,我们认为是带符号的int,所以4字节,占32位。
假设100亿个数字保存在一个大文件中,依次读一部分文件到内存(不超过内存的限制),将每个数字用二进制表示,比较二进制的最高位(第32位,符号位,0是正,1是负),如果数字的最高位为0,则将这个数字写入 file_0文件中;如果最高位为 1,则将该数字写入file_1文件中。
从而将100亿个数字分成了两个文件,假设 file_0文件中有 60亿 个数字,file_1文件中有 40亿 个数字。那么中位数就在 file_0 文件中,并且是 file_0 文件中所有数字排序之后的第 10亿 个数字。(file_1中的数都是负数,file_0中的数都是正数,也即这里一共只有40亿个负数,那么排序之后的第50亿个数一定位于file_0中)
现在,我们只需要处理 file_0 文件了(不需要再考虑file_1文件)。对于 file_0 文件,同样采取上面的措施处理:将file_0文件依次读一部分到内存(不超内存限制),将每个数字用二进制表示,比较二进制的 次高位(第31位),如果数字的次高位为0,写入file_0_0文件中;如果次高位为1,写入file_0_1文件 中。
现假设 file_0_0文件中有30亿个数字,file_0_1中也有30亿个数字,则中位数就是:file_0_0文件中的数字从小到大排序之后的第10亿个数字。
抛弃file_0_1文件,继续对 file_0_0文件 根据 次次高位(第30位) 划分,假设此次划分的两个文件为:file_0_0_0中有5亿个数字,file_0_0_1中有25亿个数字,那么中位数就是 file_0_0_1文件中的所有数字排序之后的 第 5亿 个数。
按照上述思路,直到划分的文件可直接加载进内存时,就可以直接对数字进行快速排序,找出中位数了。
9、设计短域名系统,将长URL转化成短的URL.
(1)利用放号器,初始值为0,对于每一个短链接生成请求,都递增放号器的值,再将此值转换为62进制(a-zA-Z0-9),比如第一次请求时放号器的值为0,对应62进制为a,第二次请求时放号器的值为1,对应62进制为b,第10001次请求时放号器的值为10000,对应62进制为sBc。
(2)将短链接服务器域名与放号器的62进制值进行字符串连接,即为短链接的URL,比如:t.cn/sBc。
(3)重定向过程:生成短链接之后,需要存储短链接到长链接的映射关系,即sBc -> URL,浏览器访问短链接服务器时,根据URL Path取到原始的链接,然后进行302重定向。映射关系可使用K-V存储,比如Redis或Memcache。
10、让你系统的设计一个高并发的架构,你会从哪几个方面考虑?
系统拆分
总结:绘上一张Kakfa架构思维大纲脑图(xmind)
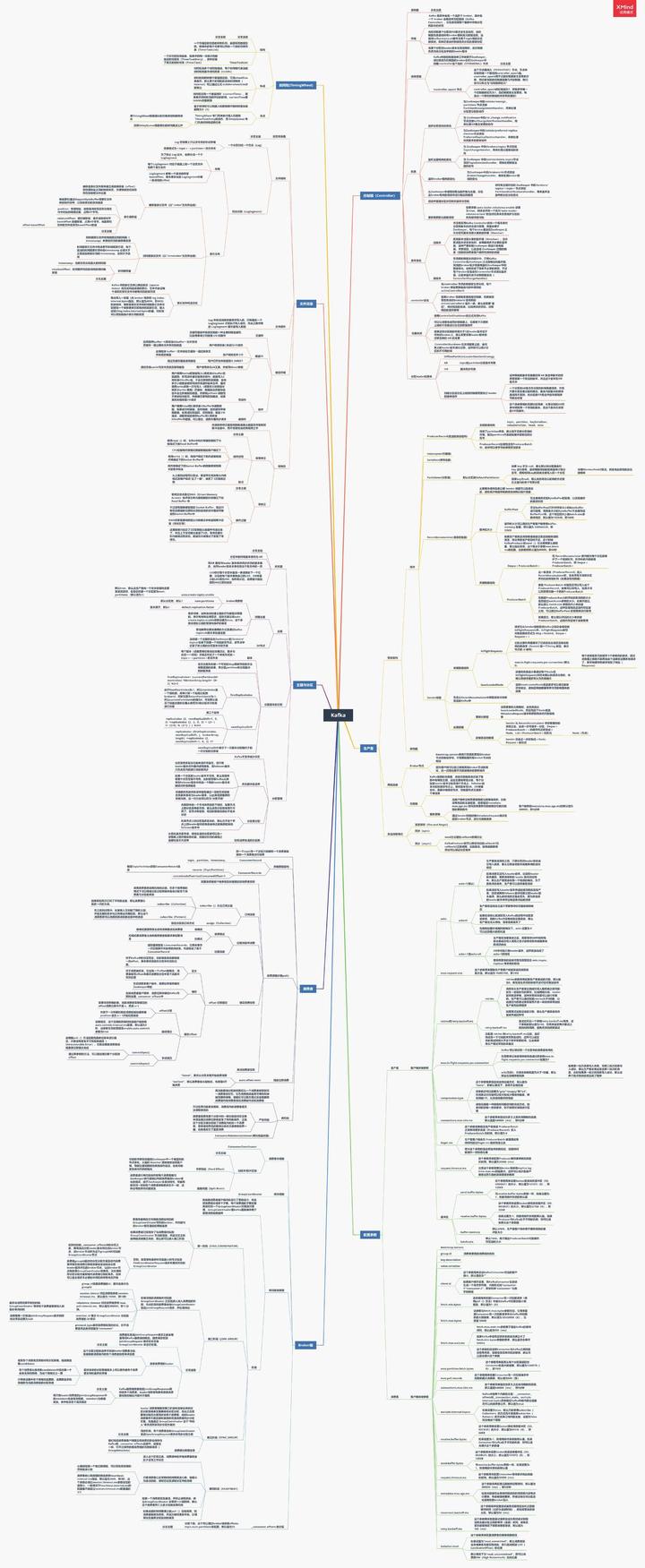
其实关于Kafka,能问的问题实在是太多了,扒了几天,最终筛选出44问:基础篇17问、进阶篇15问、高级篇12问,个个直戳痛点,不知道如果你不着急看答案,又能答出几个呢?
若是对Kafka的知识还回忆不起来,不妨先看我手绘的知识总结脑图(xmind不能上传,文章里用的是图片版)进行整体架构的梳理
梳理了知识,刷完了面试,如若你还想进一步的深入学习解读kafka以及源码,那么接下来的这份《手写“kafka”》将会是个不错的选择。
-
Kafka入门
-
为什么选择Kafka
-
Kafka的安装、管理和配置
-
Kafka的集群
-
第一个Kafka程序
-
Kafka的生产者
-
Kafka的消费者
-
深入理解Kafka
-
可靠的数据传递
-
Spring和Kafka的整合
-
SpringBoot和Kafka的整合
-
Kafka实战之削峰填谷
-
数据管道和流式处理(了解即可)
Kafka的生产者
-
Kafka的消费者
-
深入理解Kafka
-
可靠的数据传递
-
Spring和Kafka的整合
-
SpringBoot和Kafka的整合
-
Kafka实战之削峰填谷
-
数据管道和流式处理(了解即可)
[外链图片转存中…(img-kmBINImi-1628394066652)]
