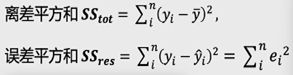题目:现有某商场2020年1-9月实际销售额数据,需要预测10月销售额数据,以便制定10月目标,数据如下

①算术平均法
计算1~9月的算术平均数即可
=AVERAGE(B4:J4)
②加权平均法
距离10月越近的数字是越有价值的,所以要对每个月的销售额进行加权平均计算,先在单元格中加入权重值,再用函数进行计算
=SUM(B6:J6)/SUM(B5:J5)
或者直接使用SUMPRODUCT:
=SUMPRODUCT(B4:J4,B5:J5)/SUM(B5:J5)
③移动平均法
根据最近一组销售数据来推断未来销售数据,一般一组是两个数据以上
举例:7~9月的销售额相加后再除以4,得到平均数据即可预测10月数据
=SUM(G4:J4)/COUNT(G4:J4)
④加权移动平均法
加权平均法与移动平均法相结合,如三个月移动平均,分别给这三个月按照离10月的距离进行赋权,确认好加几个以后在单元格内输入权重值,然后使用SUMPRODUCT
=SUMPRODUCT(H4:J4,B5:D5)/SUM(B5:D5)
⑤回归预测法
使用一元线性回归方程进行预测
y=ax+b
选择1~9月的数据 - 插入 - 折线图,点击右上角加号显示趋势线,选择线性,然后选择显示公式和R平方值,可以得到线性回归方程为
y=-121.58x+8418.6
R2=0.2053
然后将x=10带入,就可以得到结果7203
1、R2也叫决定系数,公式:
离差平方和:代表因变量的波动,即因变量实际值与其平均值之间的差值平方和。(实际值与其平均值之间的差值平方和)
误差平方和:代表因变量实际值与模型拟合值之间的误差大小。(实际值与模型预测值之间的误差平方和)
故R方可以解释因变量波动中,被模型拟合的百分比,即R方可以衡量模型拟合数据的好坏程度;R方的取值范围<=1,R方越大,模型对数据的拟合程度越好。
0.9~1.0是强相关,0.7 ~ 0.9是相关性有点强,0.5 ~0.7是相关性有点弱,未满0.5是相关性非常弱
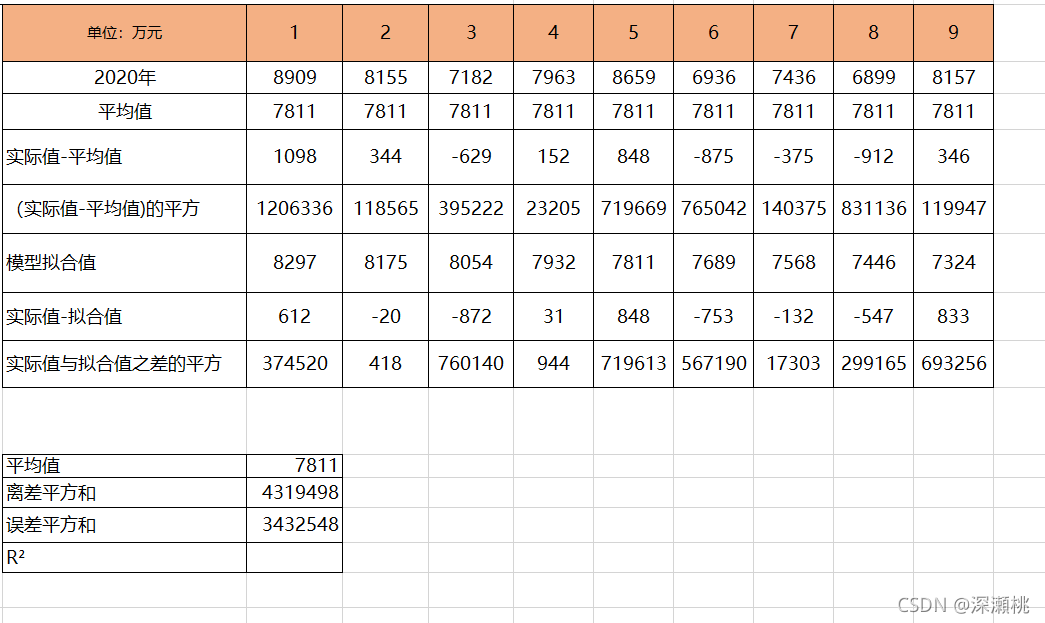
Excel中的计算方法如下
- 平均值使用average函数计算
- 实际值-平均值直接使用减法拖拽
- (实际值-平均值)的平方使用power函数,power值为2,求和后即为离差平方和
- 模型拟合值:把X值带入线性回归方程中即可得到
- 实际值-拟合值,直接进行计算即可
- 实际值 - 拟合值的平方使用power函数进行计算,求和后即为误差平方和
最后所有的数字集合如下,R2通过公式计算即可,为0.2503,此题中的R2值代表相关性非常弱
⑥业务分析法
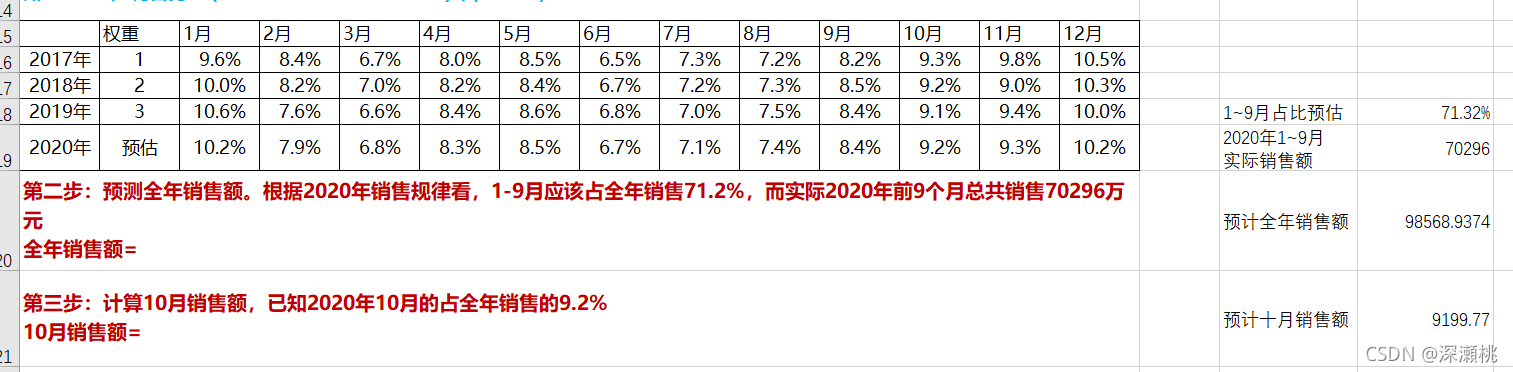
加入2017~2019年1 ~12月的数据如下图

第一步
找历史数据的规律,即每月销售额比重,其中2020年是前三年月销售百分比的加权平均数
①计算得出三年中每个月的销售额占比,表格如下图

②预估2020年每月销售比重
将上个表格中的值粘贴过来,只粘贴值,给2017~2019三年分别赋1、2、3的权重,然后哦计算2020年每个月份占比
如2020年1月占比=(9.6%*1+10%*2+10.6%*3)/(1+2+3)=10.1%)
最终得到表格如下图

第二步
预测全年销售额。根据2020年销售规律看,1-9月应该占全年销售71.3%,而实际2020年前9个月总共销售70296万元
全年销售额=70296/71.3%=98568.9
第三步
第三步:计算10月销售额,已知2020年10月的预测销售占全年销售的9.2%
10月销售额=98568.9*9.2%=9199.77万元
一般来讲,利用上面三个步骤做零售预测基本就可以了。在实际业务过程中,影响每月销售比重的因素还有:
如:在1月、2月间飘忽不定的春节因素。
这些差异性在上面计算规律的方法中没有被体现出来。
解决方案:将1月和2月合并起来计算销售比重,目的是为了剔除春节因素的影响。
总结
6种方法得到的结果如下
(1)算术平均法:7811万元
(2)加权平均法:7649万元
(3)移动平均法:三个月(即7-9月,n=3)移动平均值为7497万元,四个月(即6-9月,n=4)移动平均值为7357万元
(4)加权移动平均法:7618万元
(5)回归预测法:7203万元
(6)业务分析法:9083万元
算完这些数据后,查看前两年10月的销售数据,发现都大于当年9月的销售额,而根据数据模型算出来的预测值都小于9月份数据8157万元,这个怎么回事呢?
前5种预测方法的预测结果,不能说它们是错的,只是适用于销售量稳定,没有季节性波动的产品的预测;而传统零售行业恰恰是季节性很强的行业,要采用业务分析方法