一、简介
redis在4.0版本中引入了新的数据结构raix tree, 为了修复集群慢的问题。
“A new data structure, the radix tree (rax.c) was introduced into Redis in order to fix a major Redis Cluster slowdown. (Salvatore Sanfilippo)”
二、结构
代码4.0.0
typedef struct raxNode {
uint32_t iskey:1; /* Does this node contain a key? */
uint32_t isnull:1; /* Associated value is NULL (don't store it). */
uint32_t iscompr:1; /* Node is compressed. */
uint32_t size:29; /* Number of children, or compressed string len. */
unsigned char data[];
} raxNode;
typedef struct rax {
raxNode *head;
uint64_t numele; //元素的个数
uint64_t numnodes;//节点个数
} rax;
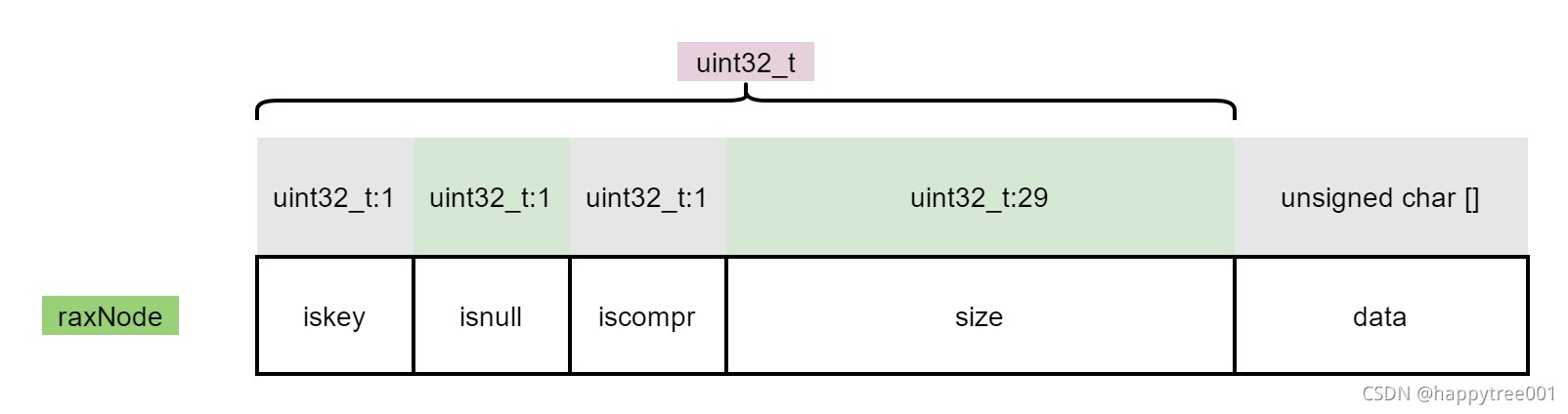
data部分的结构根据iscompr字段值进行区分
-
非压缩结构时的data结构
每一个字符都对应一个子节点

-
压缩结构
data中的数据属于一个key中的连续数据,并且只有一个子节点。

-
可选的数据部分

三、代码实现
插入
3.1 插入位置在压缩节点时
插入的位置在一个压缩节点位置时,需要对压缩节点进行拆分。
拆分压缩节点分了5种场景
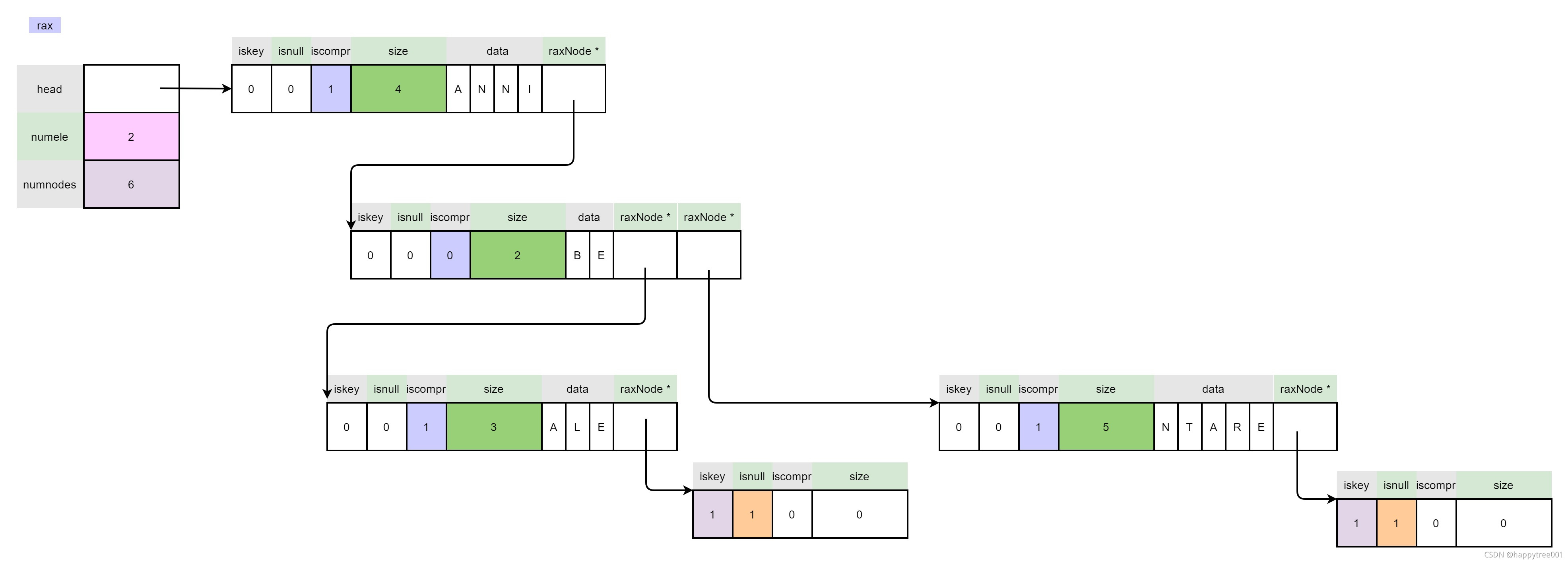
原始数据“ANNIBALE”如下:
场景1
插入“ANNIENTARE”
从中间拆分,拆分成两段
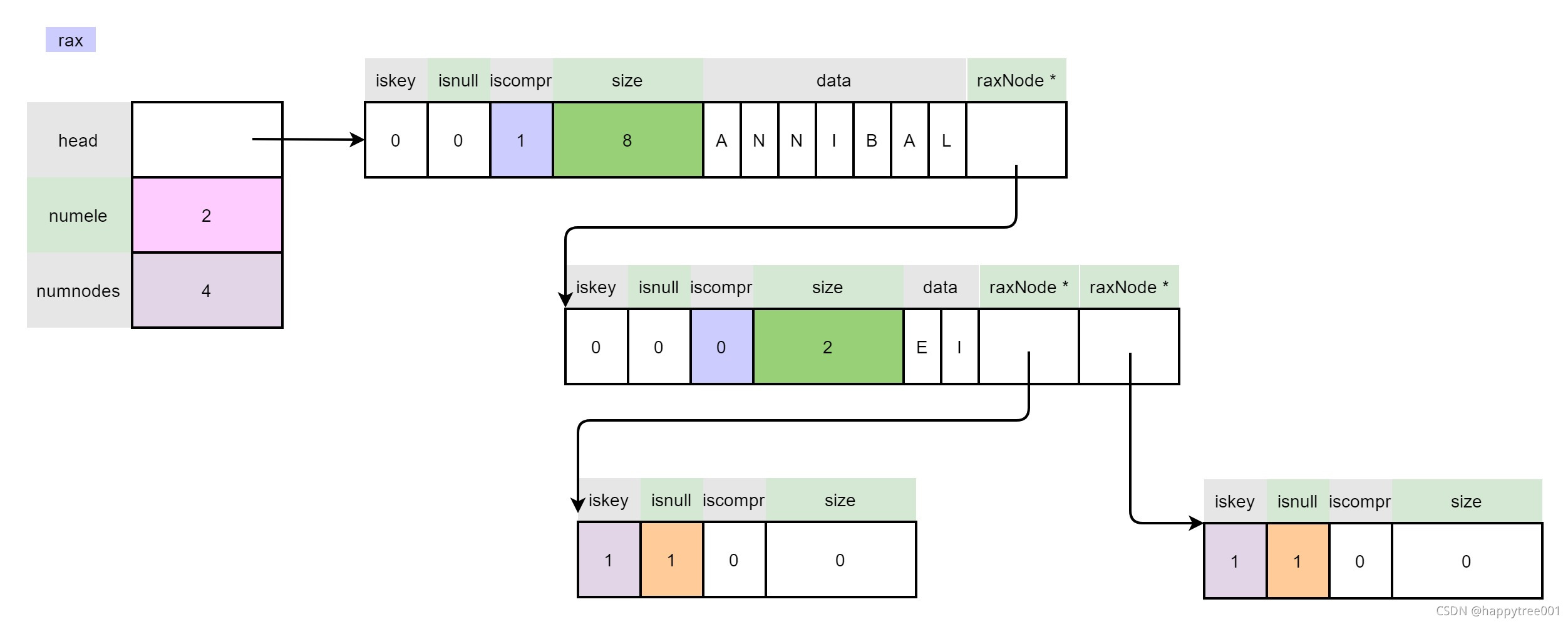
场景2
插入“ANNIBALI”
最后一个字符拆分,即只能拆分一个段,没有后段
场景3
插入“AGO”
和场景1相似,只是iscompr=0, 变为非压缩节点
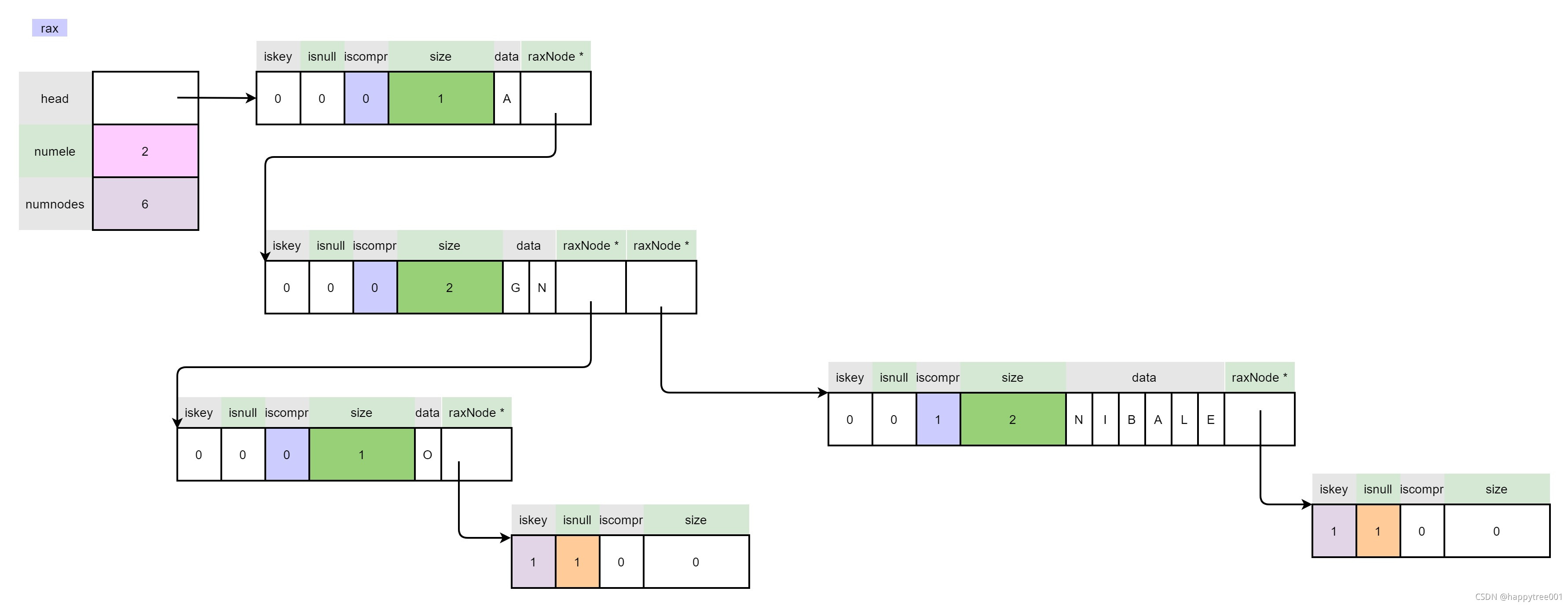
场景4
插入“CIAO”
拆分成一段,没有前段
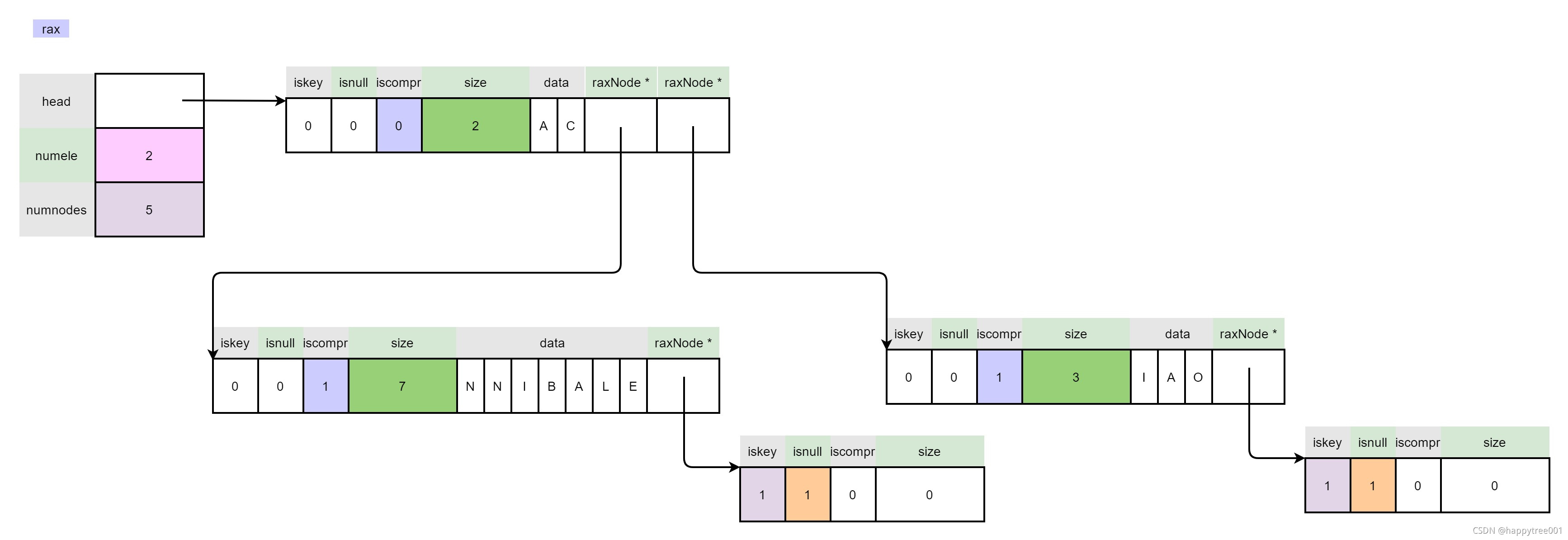
场景5
插入“ANNI”
前缀完全相同
3.2 插入非压缩节点时
创建节点,插入。
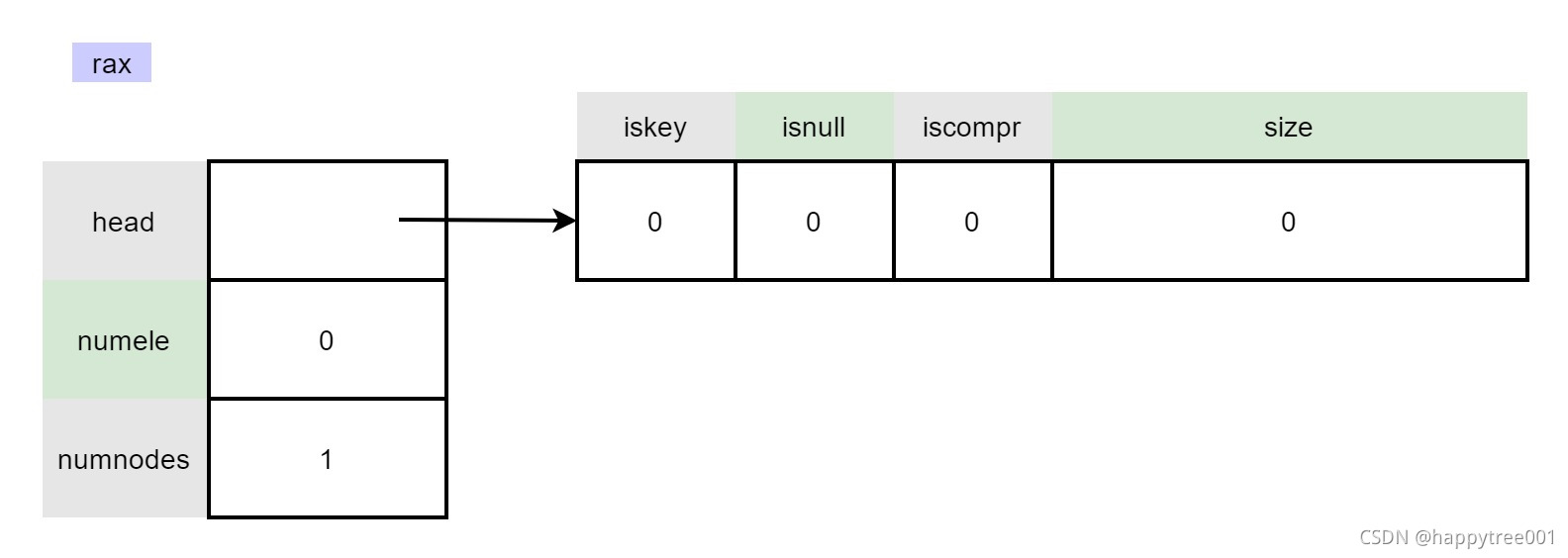
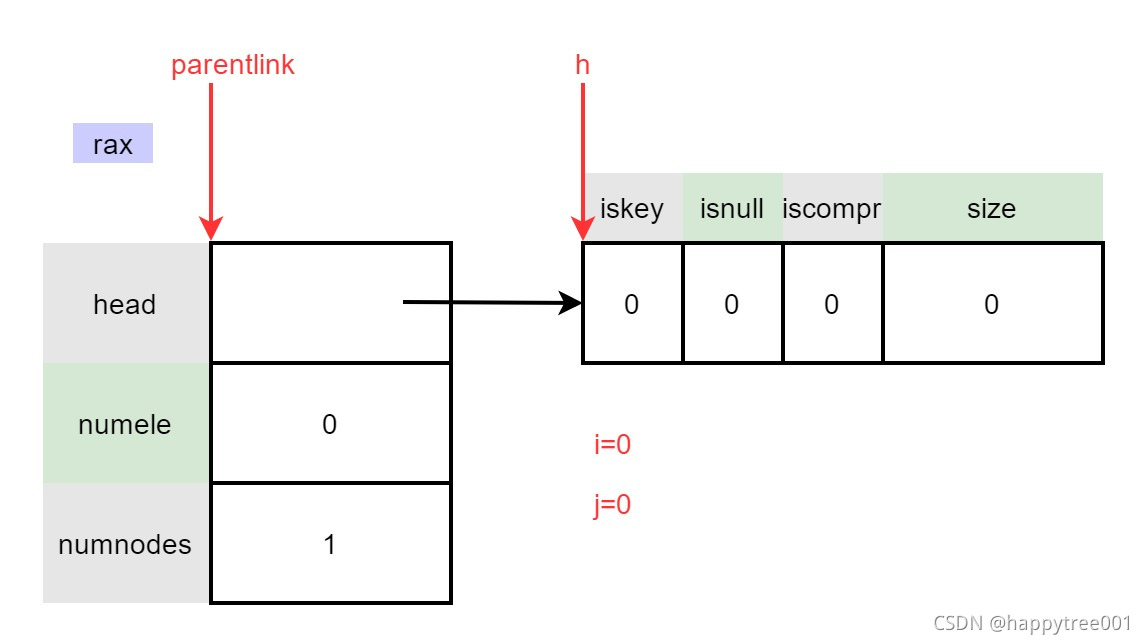
3.3 创建一个新的radix
rax *raxNew(void) {
rax *rax = rax_malloc(sizeof(*rax));
if (rax == NULL) return NULL;
rax->numele = 0;
rax->numnodes = 1;
rax->head = raxNewNode(0,0);
if (rax->head == NULL) {
rax_free(rax);
return NULL;
} else {
return rax;
}
}
raxNode *raxNewNode(size_t children, int datafield) {
size_t nodesize = sizeof(raxNode)+children+
sizeof(raxNode*)*children;
if (datafield) nodesize += sizeof(void*);
raxNode *node = rax_malloc(nodesize);
if (node == NULL) return NULL;
node->iskey = 0;
node->isnull = 0;
node->iscompr = 0;
node->size = children;
return node;
}
3.4 插入或者更新
- 当插入的元素已经存在,则直接更新data,并返回0
- 否则插入成功,返回1
- oom时也返回0,同时设置errno = ENOMEM
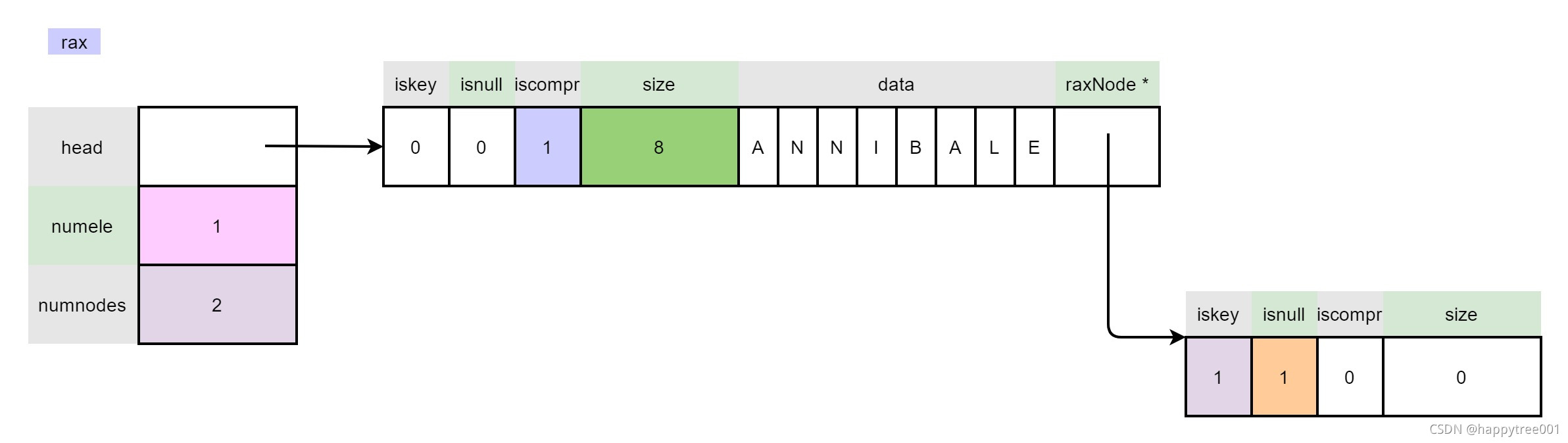
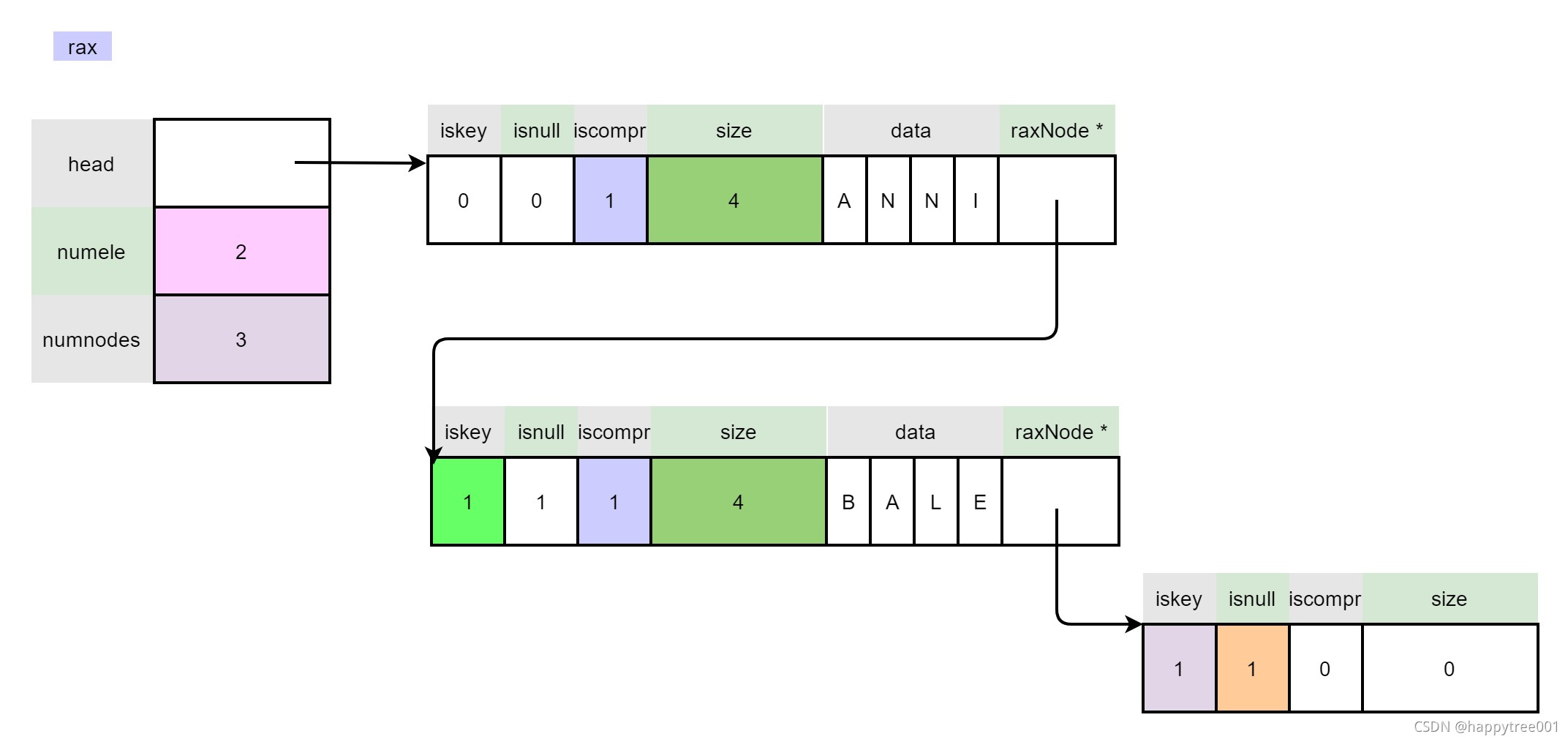
3.4.1 插入“ANNIBALE”
//插入有value
char *value = malloc(30);
strcpy(value, "hello world!");
raxInsert(rax, "ANNIBALE", 8, value, NULL) ;
3.4.1.1 首先查询到插入位置
i = raxLowWalk(rax,s,len,&h,&parentlink,&j,NULL);
static inline size_t raxLowWalk(rax *rax, unsigned char *s, size_t len, raxNode **stopnode, raxNode ***plink, int *splitpos, raxStack *ts) {
raxNode *h = rax->head;
raxNode **parentlink = &rax->head;
size_t i = 0; /* Position in the string. */
size_t j = 0; /* Position in the node children (or bytes if compressed).*/
while(h->size && i < len) {
debugnode("Lookup current node",h);
unsigned char *v = h->data;
if (h->iscompr) {
for (j = 0; j < h->size && i < len; j++, i++) {
if (v[j] != s[i]) break;
}
if (j != h->size) break;
} else {
/* Even when h->size is large, linear scan provides good
* performances compared to other approaches that are in theory
* more sounding, like performing a binary search. */
for (j = 0; j < h->size; j++) {
if (v[j] == s[i]) break;
}
if (j == h->size) break;
i++;
}
if (ts) raxStackPush(ts,h); /* Save stack of parent nodes. */
raxNode **children = raxNodeFirstChildPtr(h);
if (h->iscompr) j = 0; /* Compressed node only child is at index 0. */
memcpy(&h,children+j,sizeof(h));
parentlink = children+j;
j = 0; /* If the new node is compressed and we do not
iterate again (since i == l) set the split
position to 0 to signal this node represents
the searched key. */
}
if (stopnode) *stopnode = h;
if (plink) *plink = parentlink;
if (splitpos && h->iscompr) *splitpos = j;
return i;
}
3.4.1.2 插入节点为非压缩节点
前面的逻辑都不满足,直接进入插入逻辑
while(i < len) {
raxNode *child;
/* If this node is going to have a single child, and there
* are other characters, so that that would result in a chain
* of single-childed nodes, turn it into a compressed node. */
if (h->size == 0 && len-i > 1) {
debugf("Inserting compressed node\n");
size_t comprsize = len-i;
if (comprsize > RAX_NODE_MAX_SIZE)
comprsize = RAX_NODE_MAX_SIZE;
raxNode *newh = raxCompressNode(h,s+i,comprsize,&child);
if (newh == NULL) goto oom;
h = newh;
memcpy(parentlink,&h,sizeof(h));
parentlink = raxNodeLastChildPtr(h);
i += comprsize;
} else {
debugf("Inserting normal node\n");
raxNode **new_parentlink;
raxNode *newh = raxAddChild(h,s[i],&child,&new_parentlink);
if (newh == NULL) goto oom;
h = newh;
memcpy(parentlink,&h,sizeof(h));
parentlink = new_parentlink;
i++;
}
rax->numnodes++;
h = child;
}
- 本例子中满足
if (h->size == 0 && len-i > 1),所以插入一个压缩节点
//raxCompressNode(h, "ANNIBALE", 8, &child)
raxNode *raxCompressNode(raxNode *n, unsigned char *s, size_t len, raxNode **child) {
assert(n->size == 0 && n->iscompr == 0);
void *data = NULL; /* Initialized only to avoid warnings. */
size_t newsize;
debugf("Compress node: %.*s\n", (int)len,s);
/* Allocate the child to link to this node. */
*child = raxNewNode(0,0);
if (*child == NULL) return NULL;
/* Make space in the parent node. */
newsize = sizeof(raxNode)+len+sizeof(raxNode*);
if (n->iskey) {
data = raxGetData(n); /* To restore it later. */
if (!n->isnull) newsize += sizeof(void*);
}
raxNode *newn = rax_realloc(n,newsize);
if (newn == NULL) {
rax_free(*child);
return NULL;
}
n = newn;
n->iscompr = 1;
n->size = len;
memcpy(n->data,s,len);
if (n->iskey) raxSetData(n,data);
raxNode **childfield = raxNodeLastChildPtr(n);
memcpy(childfield,child,sizeof(*child));
return n;
}
3.4.1.2.1 创建子节点

/* Allocate the child to link to this node. */
*child = raxNewNode(0,0);
if (*child == NULL) return NULL;
3.4.1.2.2 扩容父节点
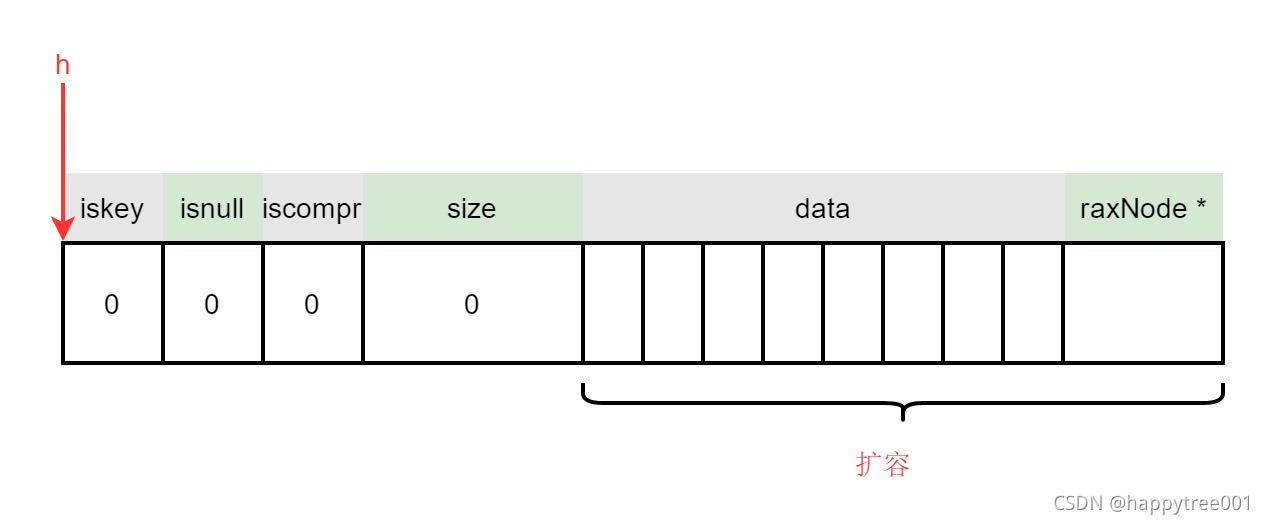
/* Make space in the parent node. */
newsize = sizeof(raxNode)+len+sizeof(raxNode*);
if (n->iskey) {
data = raxGetData(n); /* To restore it later. */
if (!n->isnull) newsize += sizeof(void*);
}
raxNode *newn = rax_realloc(n,newsize);
if (newn == NULL) {
rax_free(*child);
return NULL;
}
n = newn;
3.4.1.2.3 设置父节点信息
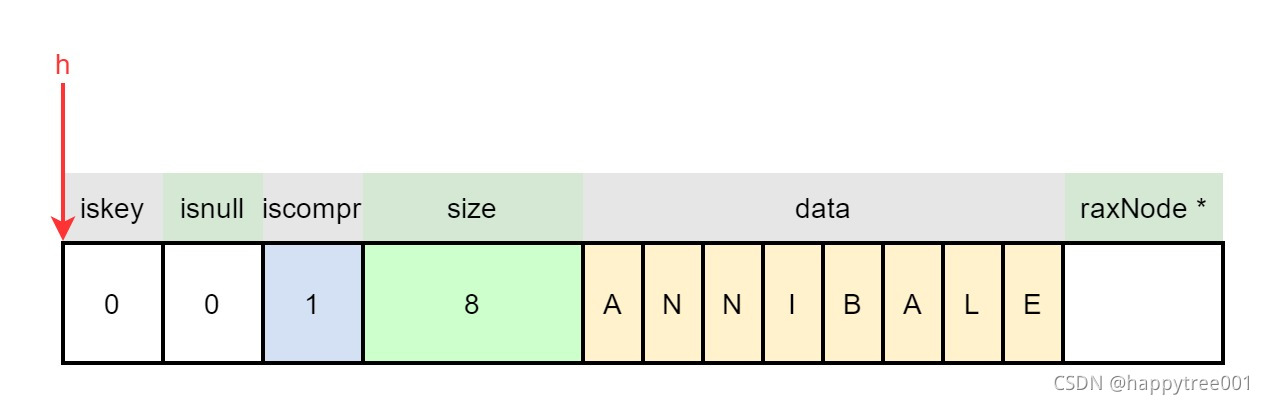
n->iscompr = 1;
n->size = len;
memcpy(n->data,s,len);
3.4.1.2.4 重新设置原有的value
//本例子中此节点不是一个key
if (n->iskey) raxSetData(n,data);
3.4.1.2.5 关联父子节点
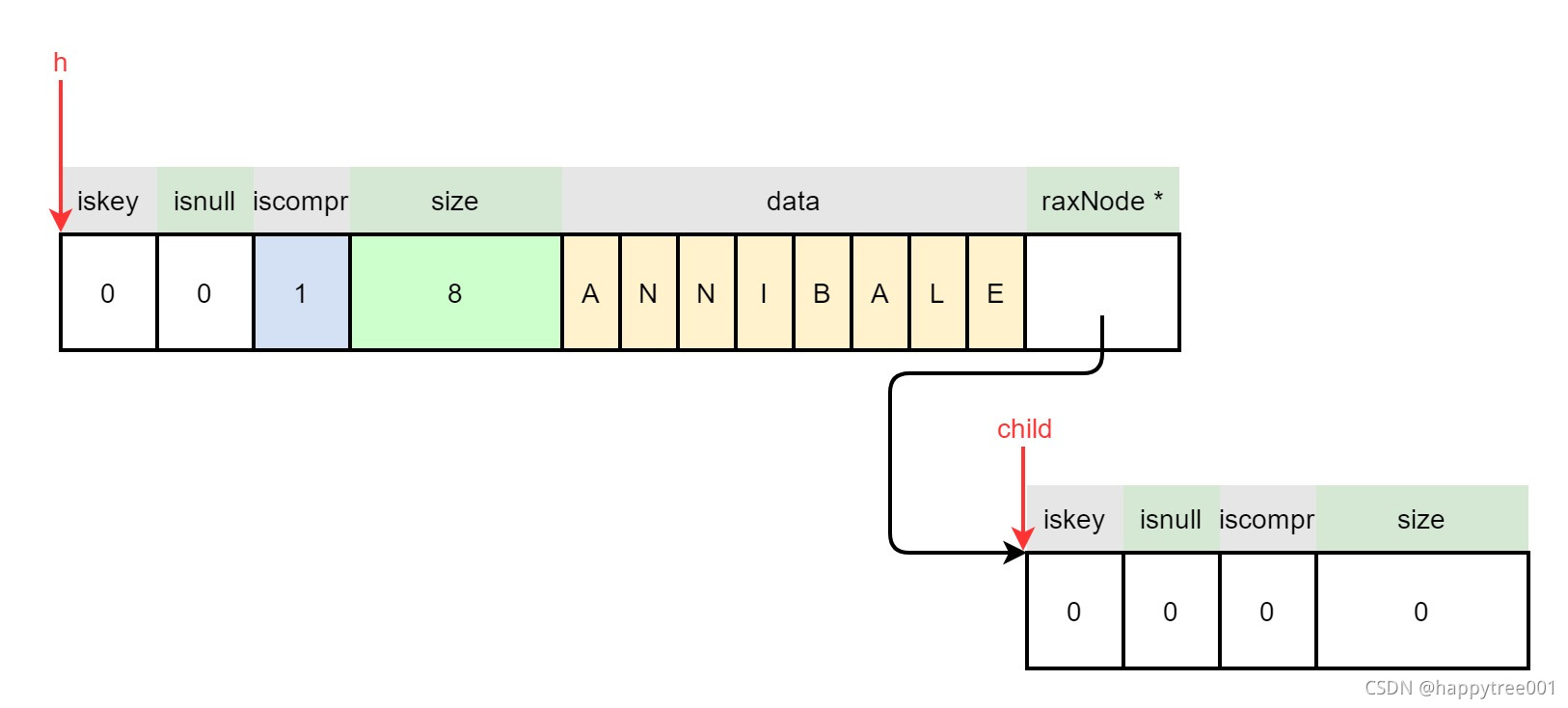
raxNode **childfield = raxNodeLastChildPtr(n);
memcpy(childfield,child,sizeof(*child));
3.4.1.2.6 重置子节点
因为h扩容了,可能地址已经改变,所以需要重新赋值
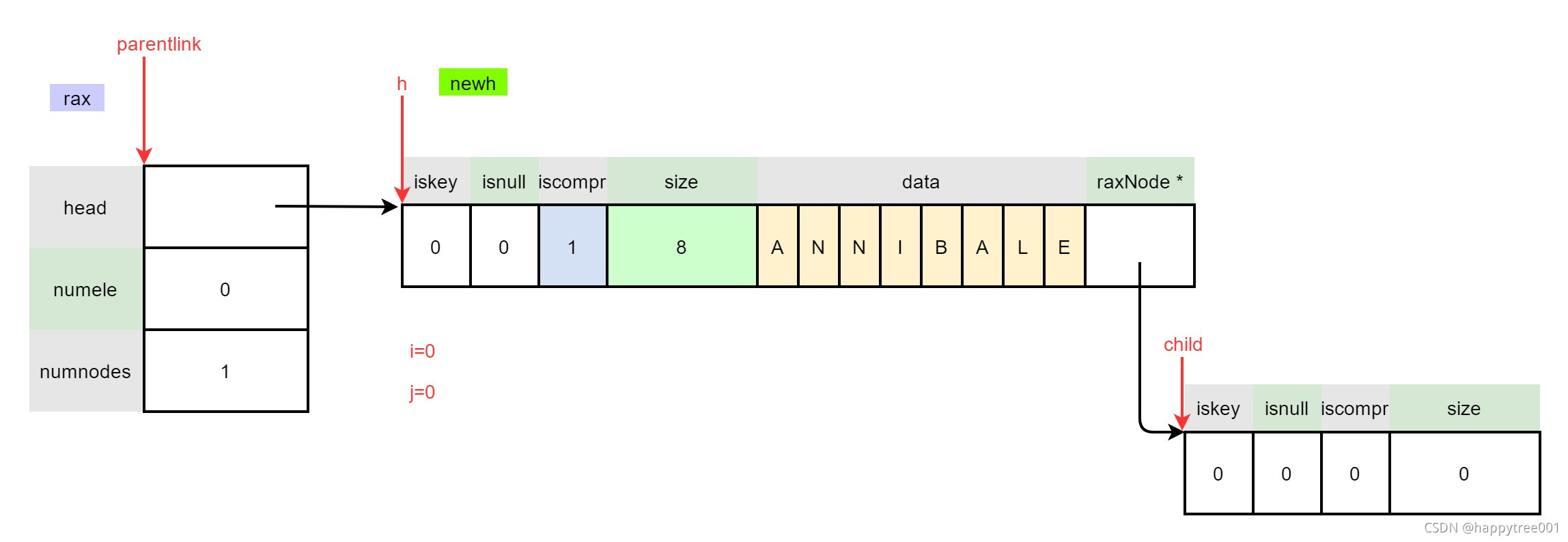
raxNode *newh = raxCompressNode(h,s+i,comprsize,&child);
if (newh == NULL) goto oom;
h = newh;
memcpy(parentlink,&h,sizeof(h));
3.4.1.2.7 移动下一个节点
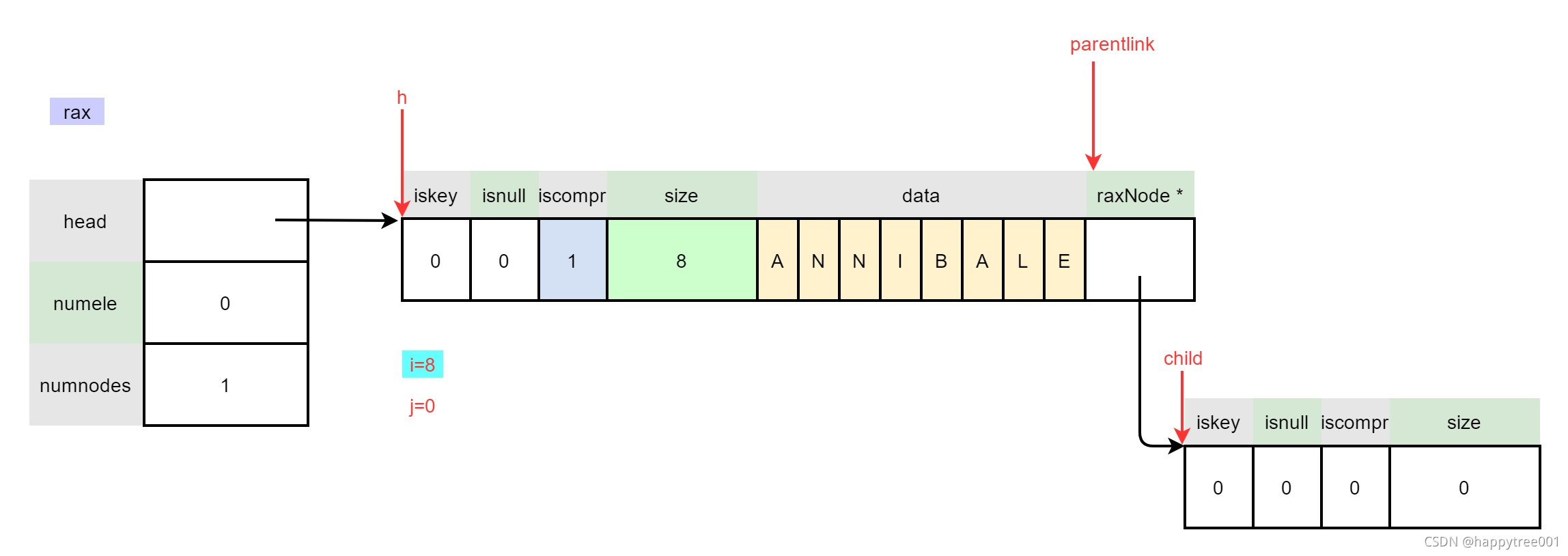
parentlink = raxNodeLastChildPtr(h);
i += comprsize;
3.4.1.2.8 节点个数增加
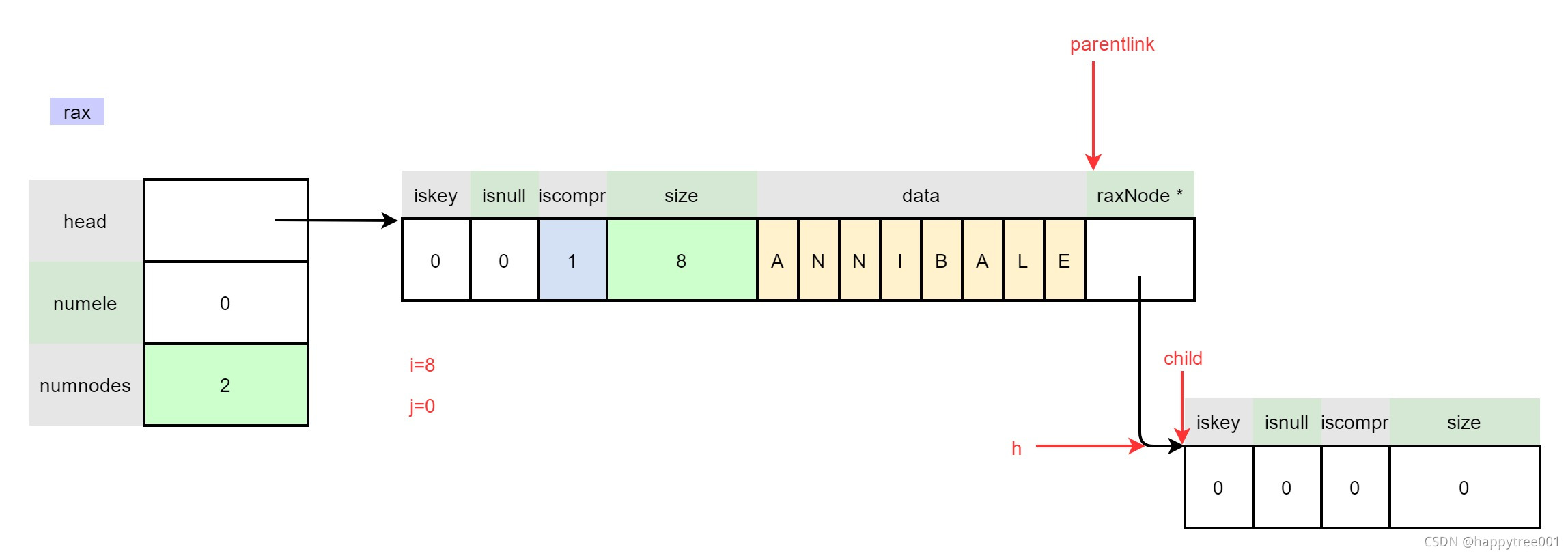
rax->numnodes++;
h = child;
3.4.1.2.9 分配数据空间
如果data为null,则不会分配空间
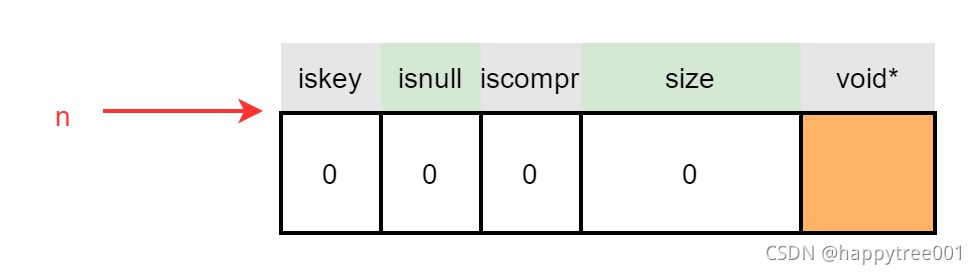
raxNode *newh = raxReallocForData(h,data);
if (newh == NULL) goto oom;
/* realloc the node to make room for auxiliary data in order
* to store an item in that node. On out of memory NULL is returned. */
raxNode *raxReallocForData(raxNode *n, void *data) {
if (data == NULL) return n; /* No reallocation needed, setting isnull=1 */
size_t curlen = raxNodeCurrentLength(n);
return rax_realloc(n,curlen+sizeof(void*));
}
3.4.1.2.10 增加key节点个数
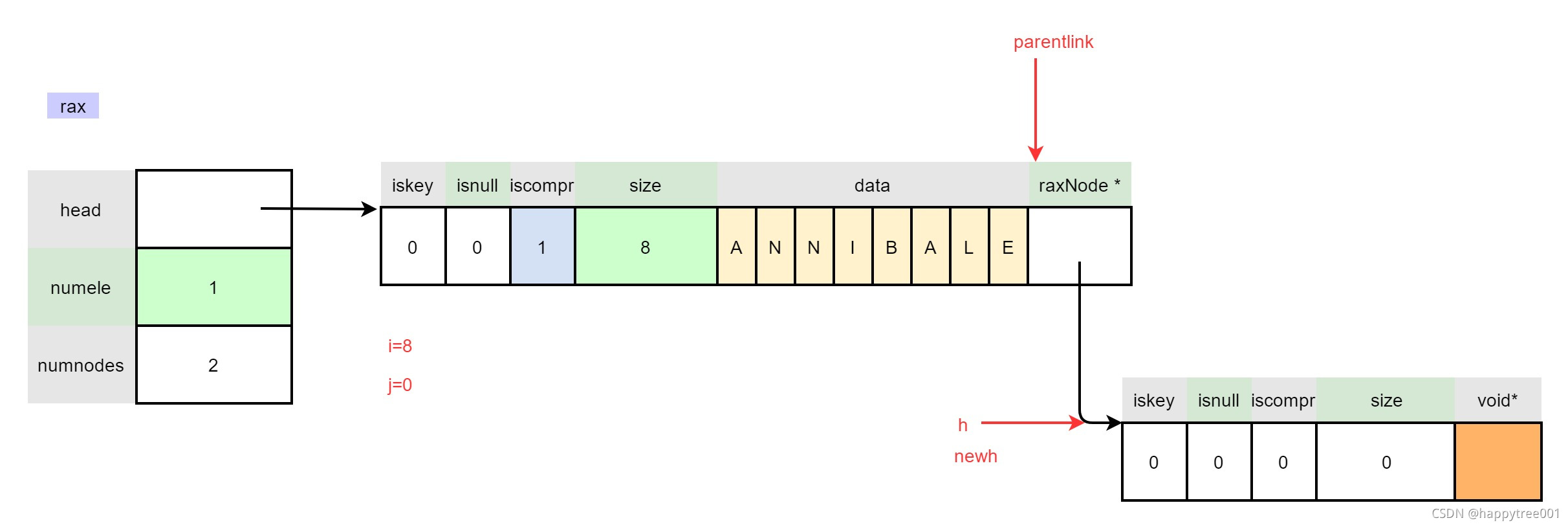
h = newh;
if (!h->iskey) rax->numele++;
3.4.1.2.11 设置value
当有data时,isnull是1, 否则isnull为0,value字段只是存放的真正值的地址
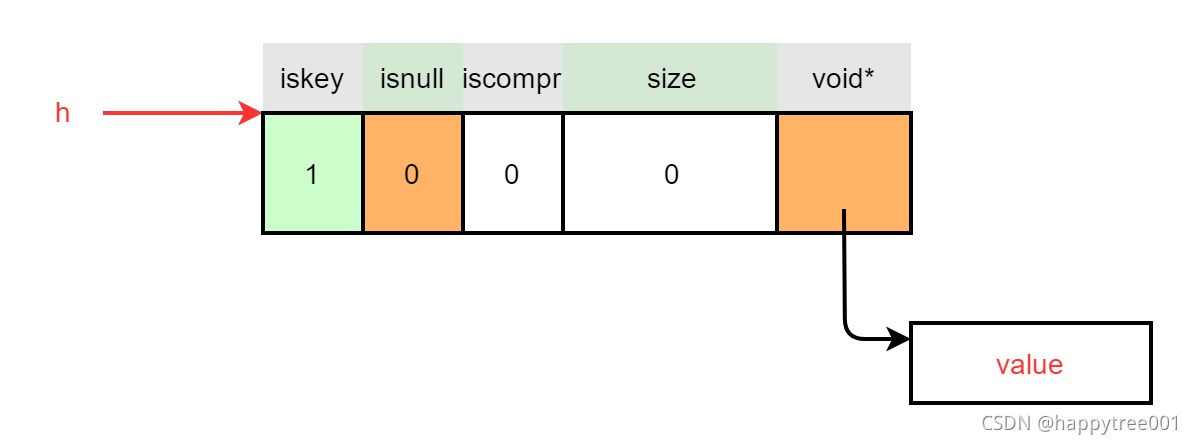
raxSetData(h,data);
/* Set the node auxiliary data to the specified pointer. */
void raxSetData(raxNode *n, void *data) {
n->iskey = 1;
if (data != NULL) {
void **ndata = (void**)
((char*)n+raxNodeCurrentLength(n)-sizeof(void*));
memcpy(ndata,&data,sizeof(data));
n->isnull = 0;
} else {
n->isnull = 1;
}
}
3.4.1.2.12 重置子节点
因为在h设置value扩容,地址可能修改
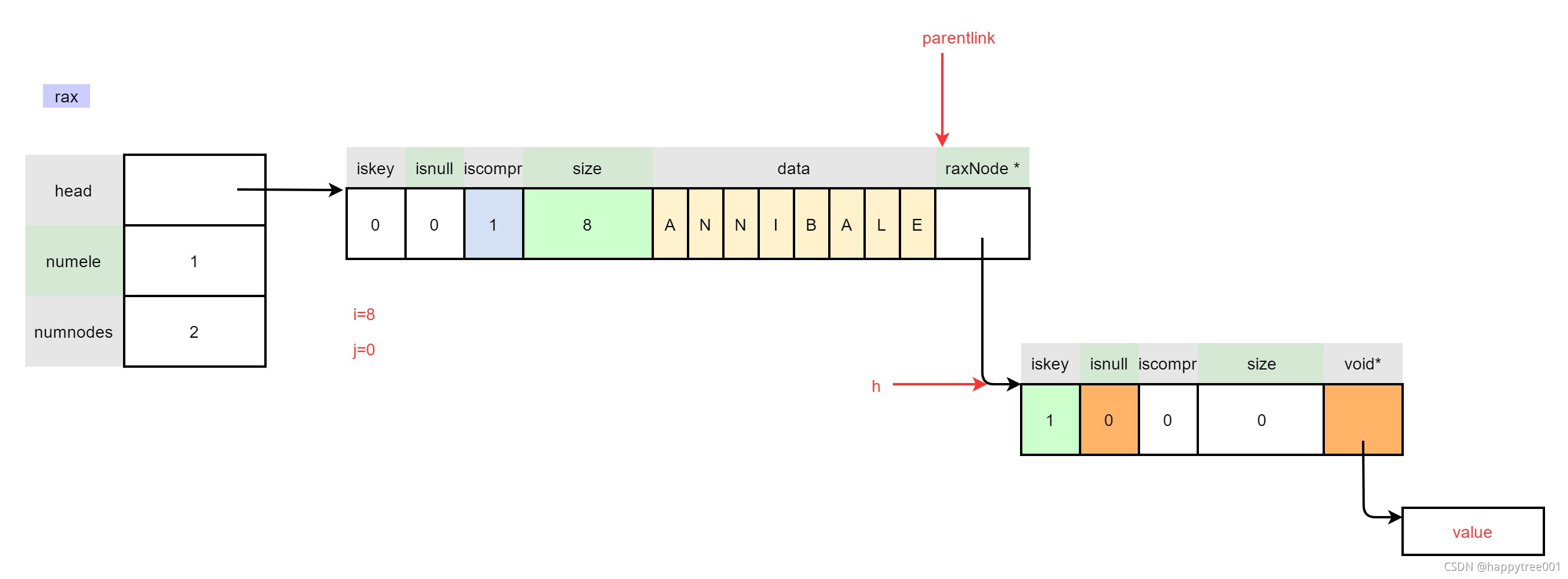
memcpy(parentlink,&h,sizeof(h));
return 1; /* Element inserted. */
3.4.2 插入"ANNIENTARE"
raxInsert(rax, "ANNIENTARE", 10, NULL, NULL) ;
3.4.2.1 定位插入位置
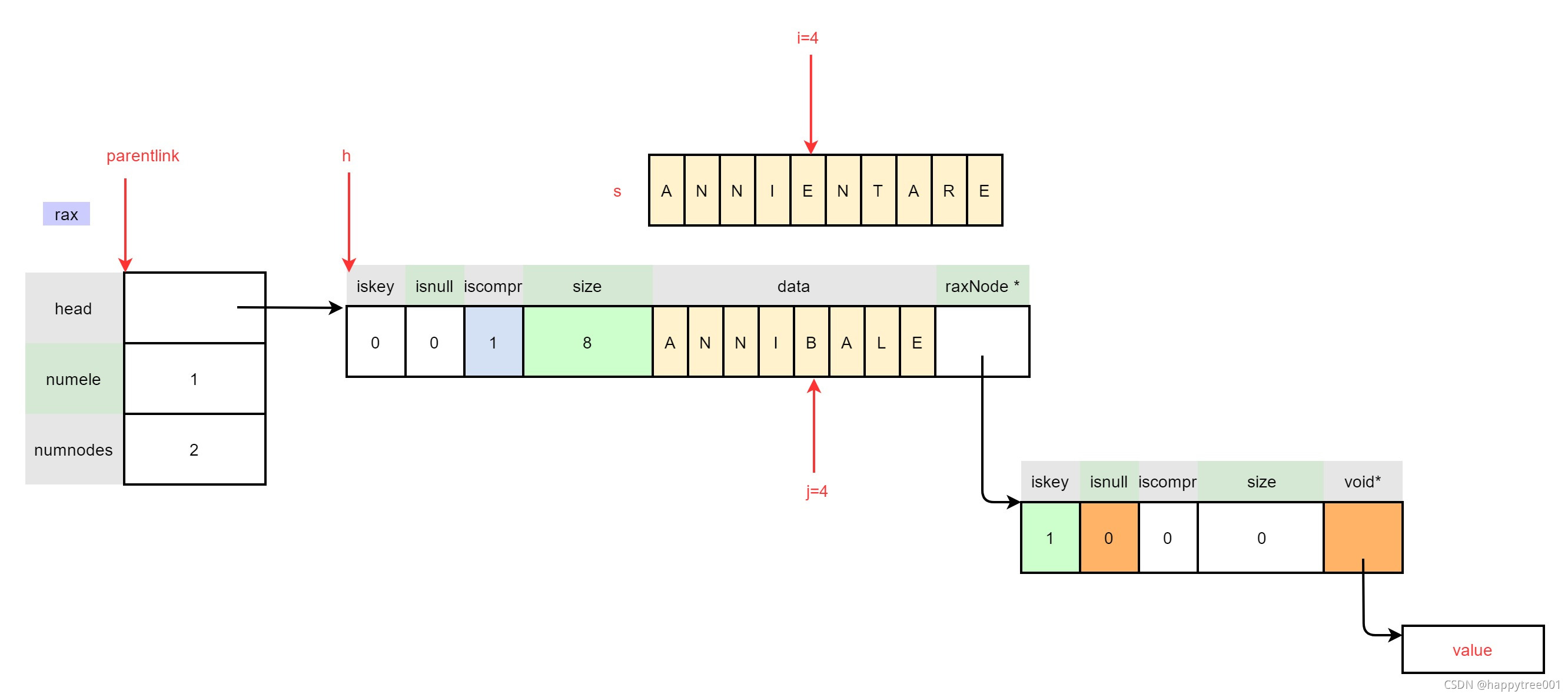
3.4.2.2 插入节点为压缩节点
- 确定算法
当前例子满足算法1
/* ------------------------- ALGORITHM 1 --------------------------- */
if (h->iscompr && i != len) {
3.4.2.2.1 保存next指针
/* 1: Save next pointer. */
raxNode **childfield = raxNodeLastChildPtr(h);
raxNode *next;
memcpy(&next,childfield,sizeof(next));
...
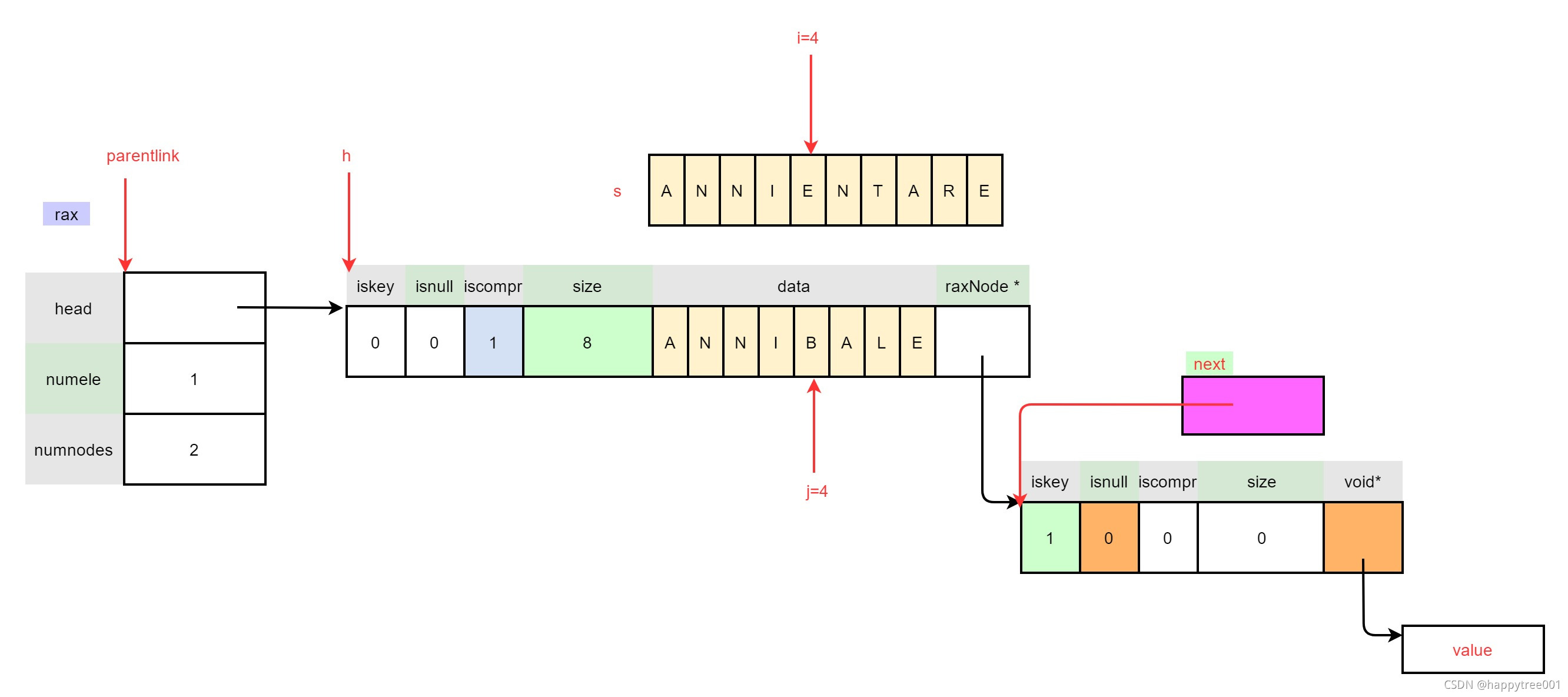
3.4.2.2.2 创建拆分节点
/* Set the length of the additional nodes we will need. */
size_t trimmedlen = j;
size_t postfixlen = h->size - j - 1;
int split_node_is_key = !trimmedlen && h->iskey && !h->isnull;
size_t nodesize;
/* 2: Create the split node. Also allocate the other nodes we'll need
* ASAP, so that it will be simpler to handle OOM. */
raxNode *splitnode = raxNewNode(1, split_node_is_key);
raxNode *trimmed = NULL;
raxNode *postfix = NULL;
if (trimmedlen) {
nodesize = sizeof(raxNode)+trimmedlen+sizeof(raxNode*);
if (h->iskey && !h->isnull) nodesize += sizeof(void*);
trimmed = rax_malloc(nodesize);
}
if (postfixlen) {
nodesize = sizeof(raxNode)+postfixlen+
sizeof(raxNode*);
postfix = rax_malloc(nodesize);
}
/* OOM? Abort now that the tree is untouched. */
if (splitnode == NULL ||
(trimmedlen && trimmed == NULL) ||
(postfixlen && postfix == NULL))
{
rax_free(splitnode);
rax_free(trimmed);
rax_free(postfix);
errno = ENOMEM;
return 0;
}
splitnode->data[0] = h->data[j];
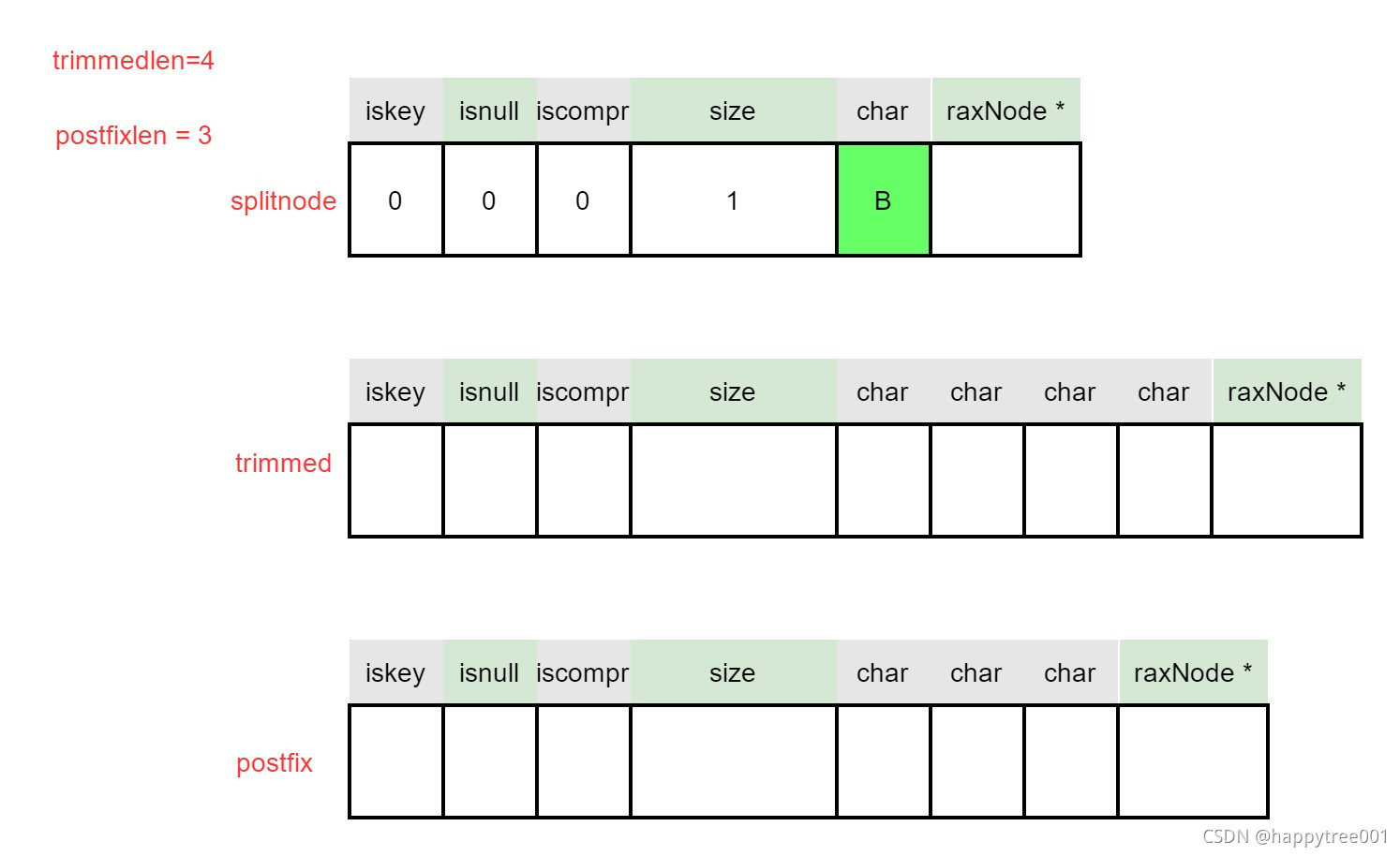
3.4.2.2.3 处理压缩节点前半部分
if (j == 0) {
/* 3a: Replace the old node with the split node. */
if (h->iskey) {
void *ndata = raxGetData(h);
raxSetData(splitnode,ndata);
}
memcpy(parentlink,&splitnode,sizeof(splitnode));
} else {
/* 3b: Trim the compressed node. */
trimmed->size = j;
memcpy(trimmed->data,h->data,j);
trimmed->iscompr = j > 1 ? 1 : 0;
trimmed->iskey = h->iskey;
trimmed->isnull = h->isnull;
if (h->iskey && !h->isnull) {
void *ndata = raxGetData(h);
raxSetData(trimmed,ndata);
}
raxNode **cp = raxNodeLastChildPtr(trimmed);
memcpy(cp,&splitnode,sizeof(splitnode));
memcpy(parentlink,&trimmed,sizeof(trimmed));
parentlink = cp; /* Set parentlink to splitnode parent. */
rax->numnodes++;
}
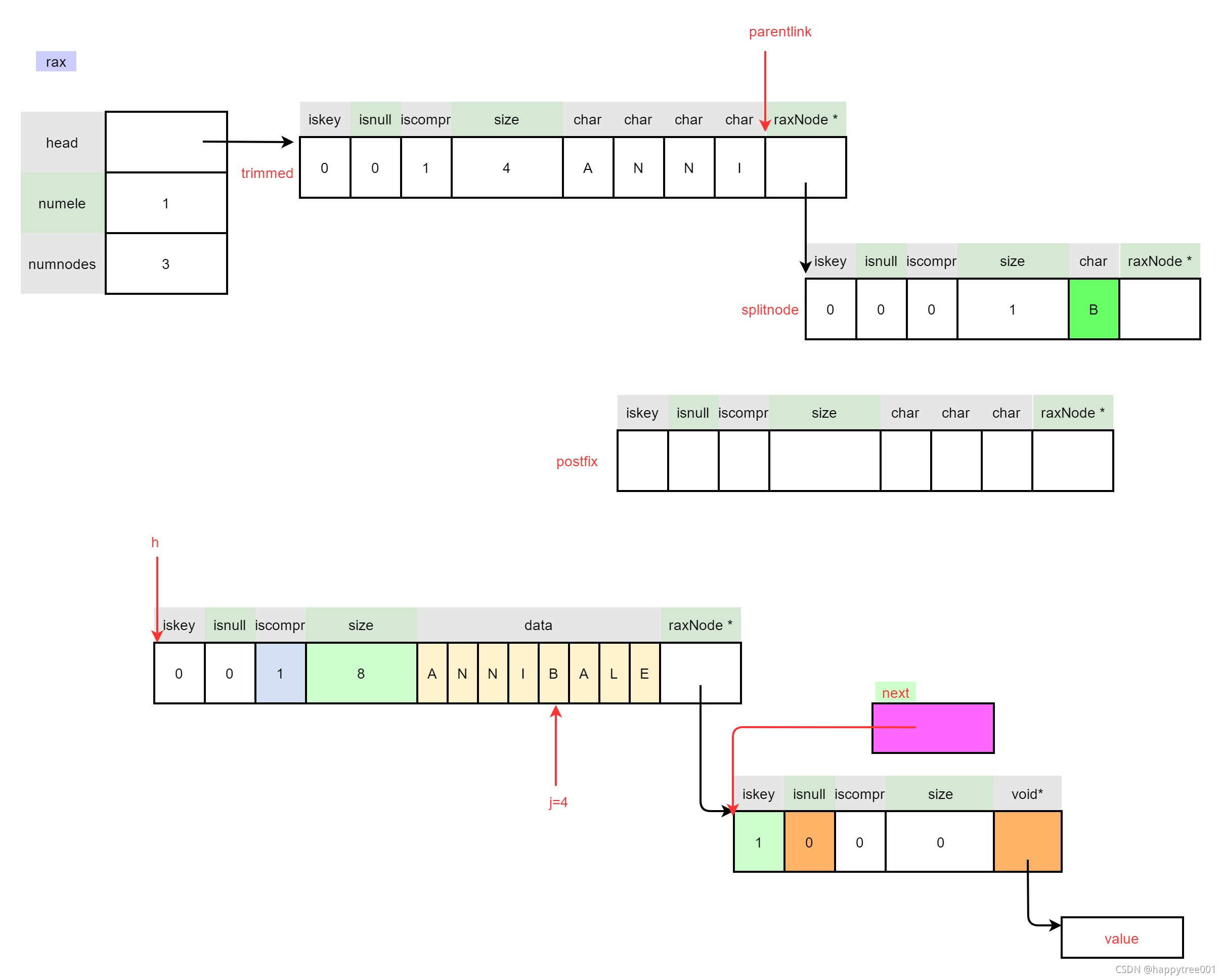
3.4.2.2.4 处理压缩节点后半部分
/* 4: Create the postfix node: what remains of the original
* compressed node after the split. */
if (postfixlen) {
/* 4a: create a postfix node. */
postfix->iskey = 0;
postfix->isnull = 0;
postfix->size = postfixlen;
postfix->iscompr = postfixlen > 1;
memcpy(postfix->data,h->data+j+1,postfixlen);
raxNode **cp = raxNodeLastChildPtr(postfix);
memcpy(cp,&next,sizeof(next));
rax->numnodes++;
} else {
/* 4b: just use next as postfix node. */
postfix = next;
}
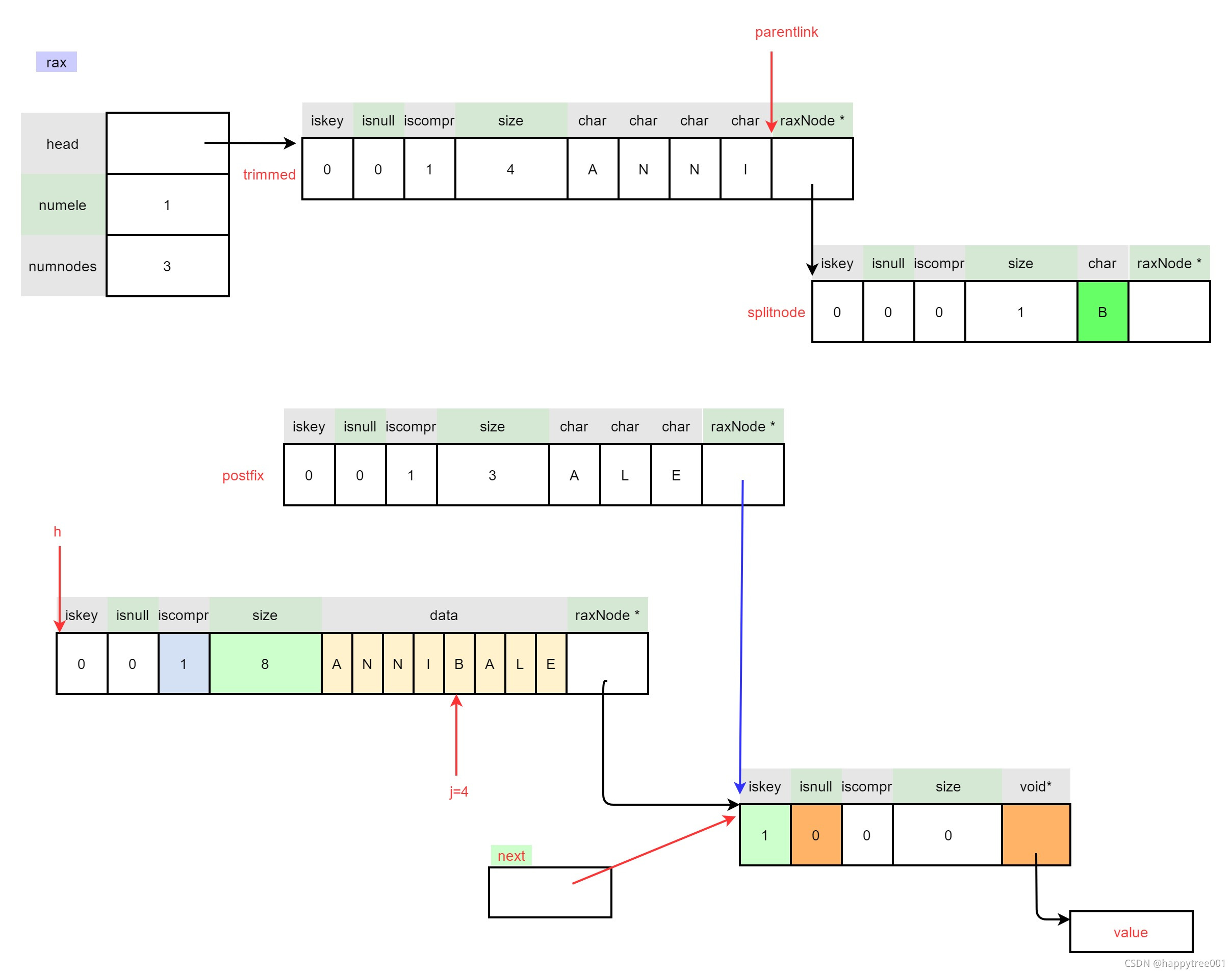
3.4.2.2.5 连接拆分节点
/* 5: Set splitnode first child as the postfix node. */
raxNode **splitchild = raxNodeLastChildPtr(splitnode);
memcpy(splitchild,&postfix,sizeof(postfix));
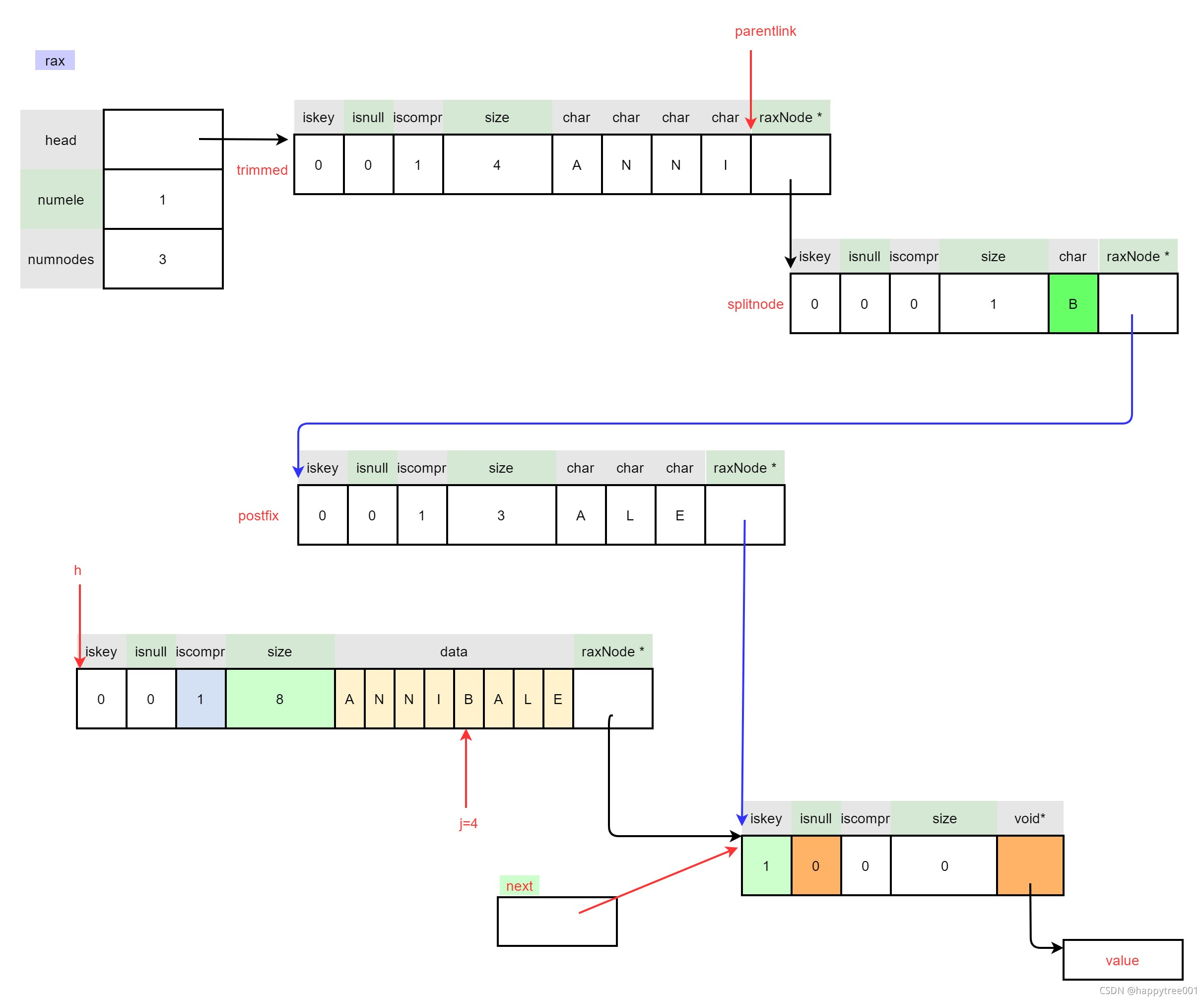
3.4.2.2.6 释放老节点
/* 6. Continue insertion: this will cause the splitnode to
* get a new child (the non common character at the currently
* inserted key). */
rax_free(h);
h = splitnode;
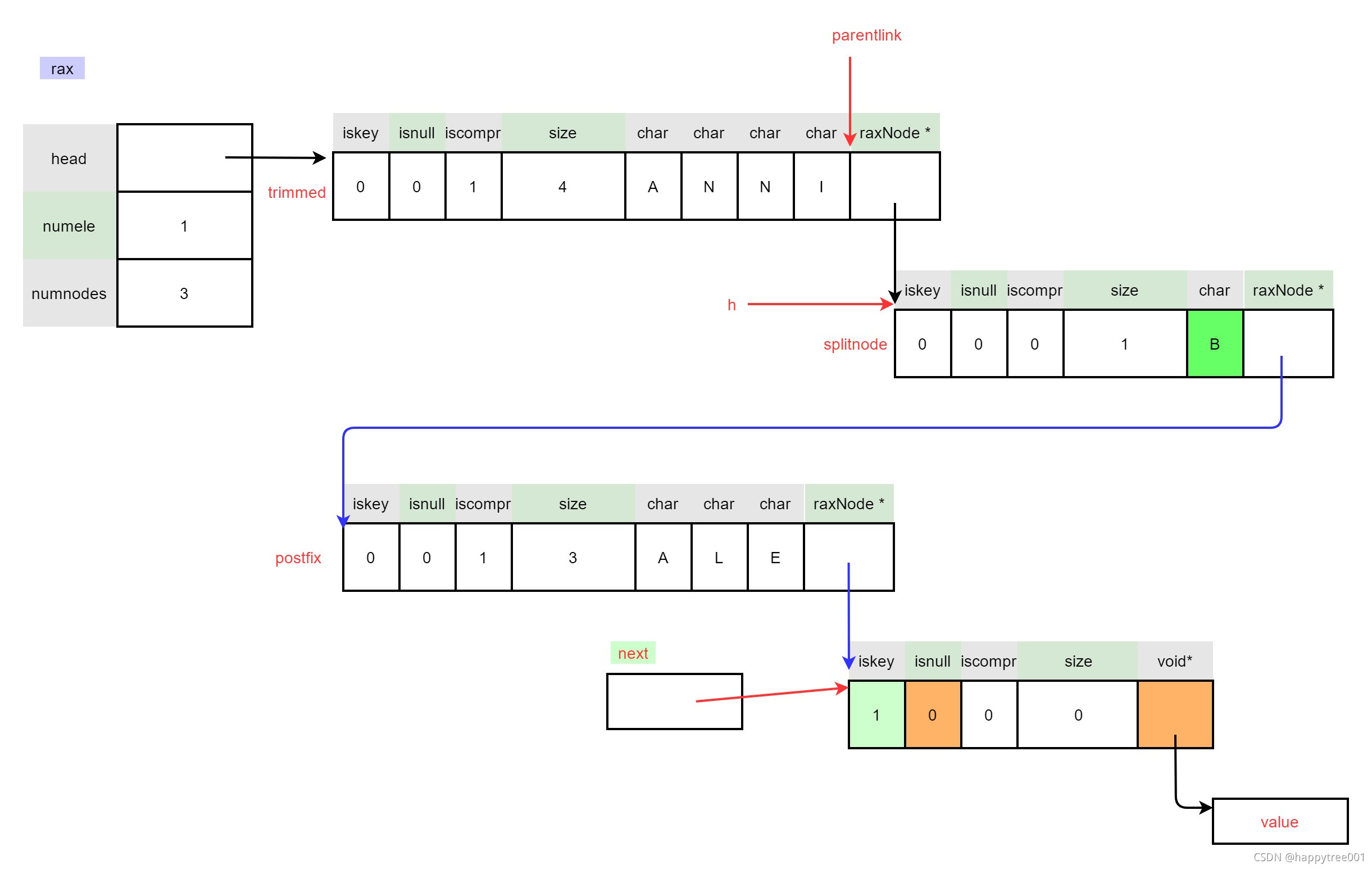
3.4.2.3 插入后续数据
3.4.2.3.1 插入剩余数据
while(i < len) {
raxNode *child;
/* If this node is going to have a single child, and there
* are other characters, so that that would result in a chain
* of single-childed nodes, turn it into a compressed node. */
if (h->size == 0 && len-i > 1) {
debugf("Inserting compressed node\n");
size_t comprsize = len-i;
if (comprsize > RAX_NODE_MAX_SIZE)
comprsize = RAX_NODE_MAX_SIZE;
raxNode *newh = raxCompressNode(h,s+i,comprsize,&child);
if (newh == NULL) goto oom;
h = newh;
memcpy(parentlink,&h,sizeof(h));
parentlink = raxNodeLastChildPtr(h);
i += comprsize;
} else {
debugf("Inserting normal node\n");
raxNode **new_parentlink;
raxNode *newh = raxAddChild(h,s[i],&child,&new_parentlink);
if (newh == NULL) goto oom;
h = newh;
memcpy(parentlink,&h,sizeof(h));
parentlink = new_parentlink;
i++;
}
rax->numnodes++;
h = child;
}
当前插入的h节点h->size == 1, 所以进入else分支
raxAddChild函数主要创建子节点,并且移动数据,将新节点插入到对应的位置(字典序)
/* Add a new child to the node 'n' representing the character 'c' and return
* its new pointer, as well as the child pointer by reference. Additionally
* '***parentlink' is populated with the raxNode pointer-to-pointer of where
* the new child was stored, which is useful for the caller to replace the
* child pointer if it gets reallocated.
*
* On success the new parent node pointer is returned (it may change because
* of the realloc, so the caller should discard 'n' and use the new value).
* On out of memory NULL is returned, and the old node is still valid. */
raxNode *raxAddChild(raxNode *n, unsigned char c, raxNode **childptr, raxNode ***parentlink) {
assert(n->iscompr == 0);
size_t curlen = sizeof(raxNode)+
n->size+
sizeof(raxNode*)*n->size;
size_t newlen;
/* Alloc the new child we will link to 'n'. */
raxNode *child = raxNewNode(0,0);
if (child == NULL) return NULL;
/* Make space in the original node. */
if (n->iskey) curlen += sizeof(void*);
newlen = curlen+sizeof(raxNode*)+1; /* Add 1 char and 1 pointer. */
raxNode *newn = rax_realloc(n,newlen);
if (newn == NULL) {
rax_free(child);
return NULL;
}
n = newn;
/* After the reallocation, we have 5/9 (depending on the system
* pointer size) bytes at the end, that is, the additional char
* in the 'data' section, plus one pointer to the new child:
*
* [numc][abx][ap][bp][xp]|auxp|.....
*
* Let's find where to insert the new child in order to make sure
* it is inserted in-place lexicographically. */
int pos;
for (pos = 0; pos < n->size; pos++) {
if (n->data[pos] > c) break;
}
/* Now, if present, move auxiliary data pointer at the end
* so that we can mess with the other data without overwriting it.
* We will obtain something like that:
*
* [numc][abx][ap][bp][xp].....|auxp| */
unsigned char *src;
if (n->iskey && !n->isnull) {
src = n->data+n->size+sizeof(raxNode*)*n->size;
memmove(src+1+sizeof(raxNode*),src,sizeof(void*));
}
/* Now imagine we are adding a node with edge 'c'. The insertion
* point is between 'b' and 'x', so the 'pos' variable value is
* To start, move all the child pointers after the insertion point
* of 1+sizeof(pointer) bytes on the right, to obtain:
*
* [numc][abx][ap][bp].....[xp]|auxp| */
src = n->data+n->size+sizeof(raxNode*)*pos;
memmove(src+1+sizeof(raxNode*),src,sizeof(raxNode*)*(n->size-pos));
/* Now make the space for the additional char in the data section,
* but also move the pointers before the insertion point in the right
* by 1 byte, in order to obtain the following:
*
* [numc][ab.x][ap][bp]....[xp]|auxp| */
src = n->data+pos;
memmove(src+1,src,n->size-pos+sizeof(raxNode*)*pos);
/* We can now set the character and its child node pointer to get:
*
* [numc][abcx][ap][bp][cp]....|auxp|
* [numc][abcx][ap][bp][cp][xp]|auxp| */
n->data[pos] = c;
n->size++;
raxNode **childfield = (raxNode**)(n->data+n->size+sizeof(raxNode*)*pos);
memcpy(childfield,&child,sizeof(child));
*childptr = child;
*parentlink = childfield;
return n;
}
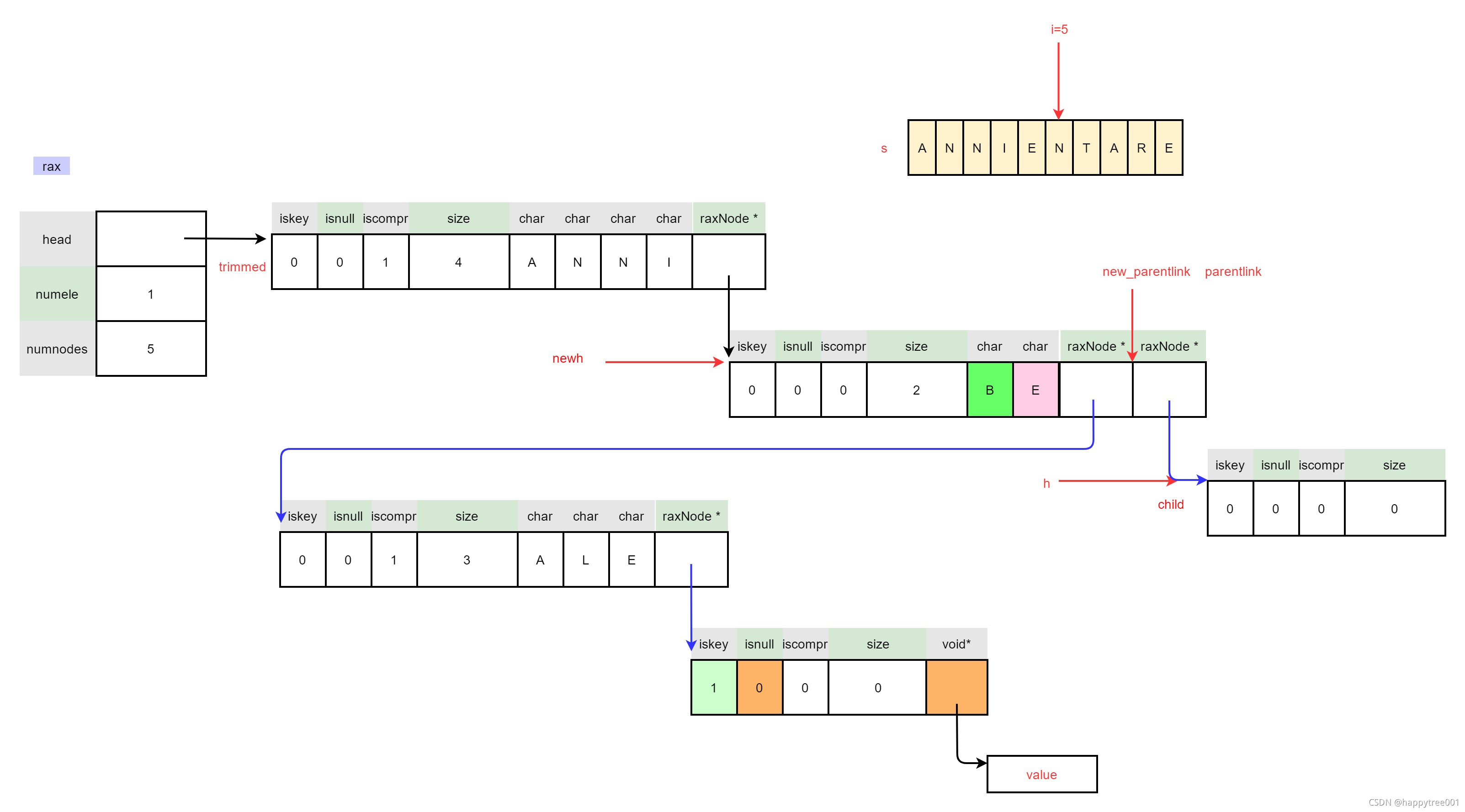
- 进入第二次while
满足 if (h->size == 0 && len-i > 1) {, 插入压缩节点
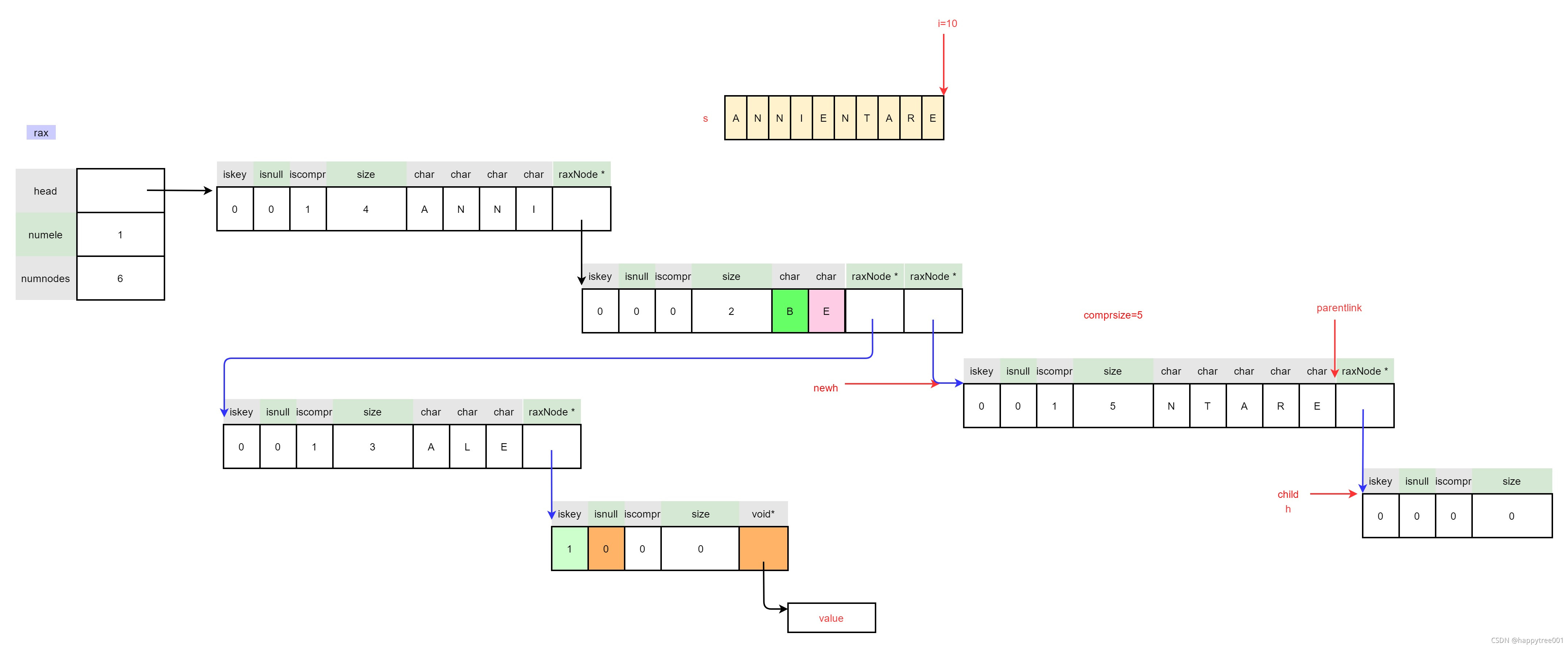
3.4.2.3.2 插入value
raxNode *newh = raxReallocForData(h,data);
if (newh == NULL) goto oom;
h = newh;
if (!h->iskey) rax->numele++;
raxSetData(h,data);
memcpy(parentlink,&h,sizeof(h));
return 1; /* Element inserted. */
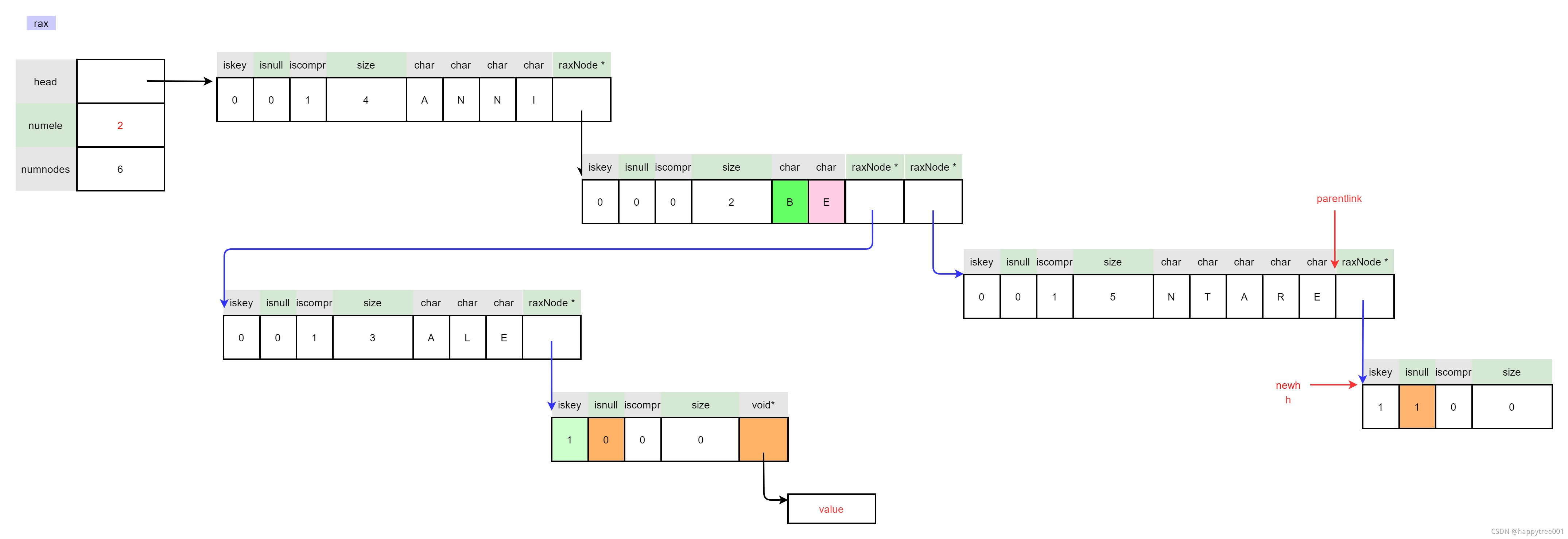
3.4.3 插入“ANNE”
raxInsert(rax, "ANNE", 4, NULL, NULL) ;
3.4.3.1 定位插入位置
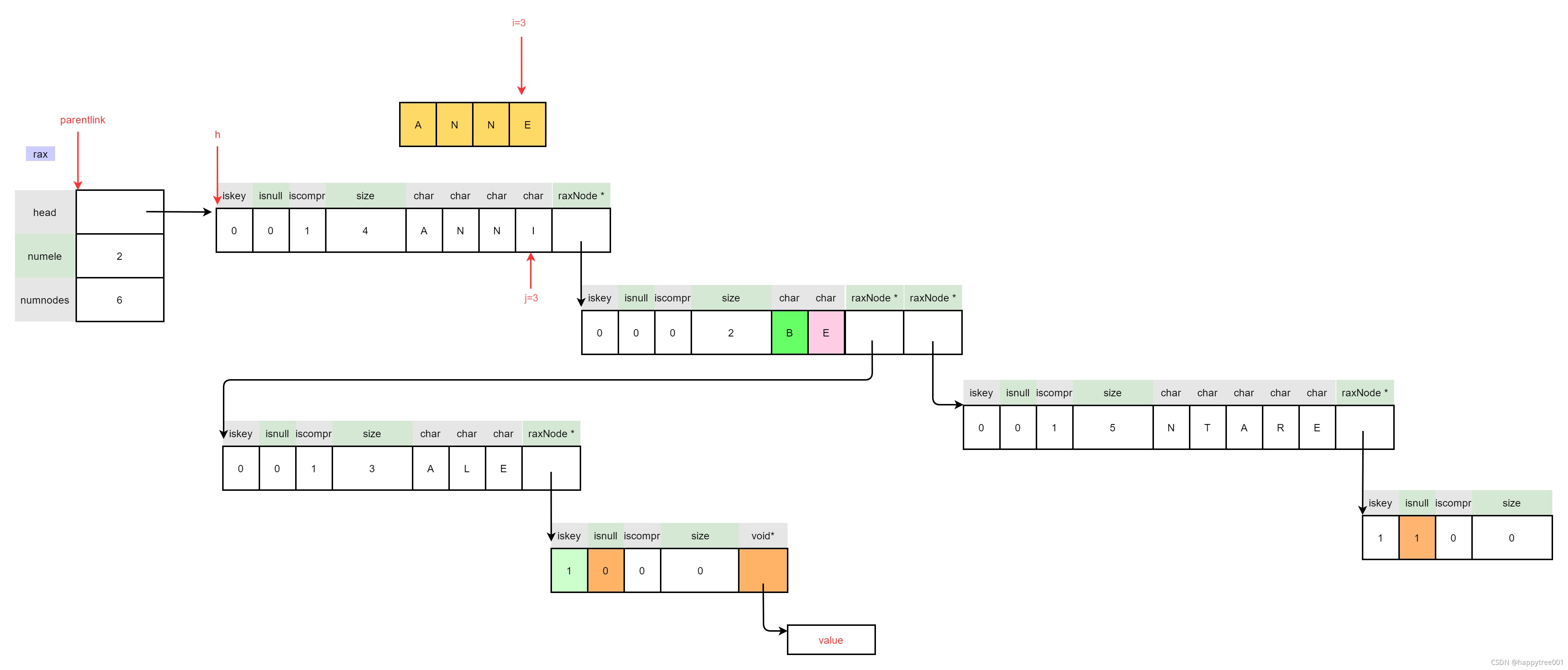
3.4.3.2 插入节点为压缩节点
满足算法1
3.4.3.2.1 保存next指针
/* 1: Save next pointer. */
raxNode **childfield = raxNodeLastChildPtr(h);
raxNode *next;
memcpy(&next,childfield,sizeof(next));
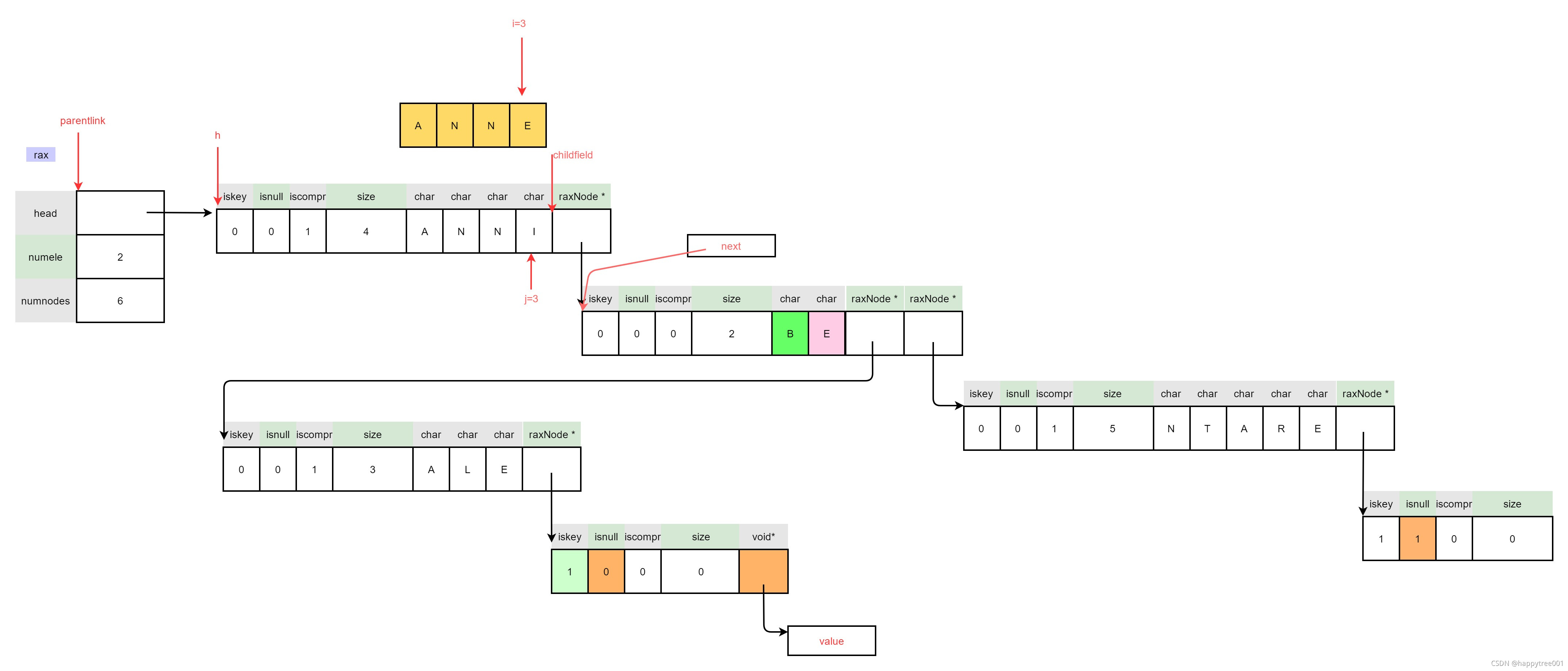
3.4.3.2.2 创建拆分节点
/* Set the length of the additional nodes we will need. */
size_t trimmedlen = j;
size_t postfixlen = h->size - j - 1;
int split_node_is_key = !trimmedlen && h->iskey && !h->isnull;
size_t nodesize;
/* 2: Create the split node. Also allocate the other nodes we'll need
* ASAP, so that it will be simpler to handle OOM. */
raxNode *splitnode = raxNewNode(1, split_node_is_key);
raxNode *trimmed = NULL;
raxNode *postfix = NULL;
if (trimmedlen) {
nodesize = sizeof(raxNode)+trimmedlen+sizeof(raxNode*);
if (h->iskey && !h->isnull) nodesize += sizeof(void*);
trimmed = rax_malloc(nodesize);
}
if (postfixlen) {
nodesize = sizeof(raxNode)+postfixlen+
sizeof(raxNode*);
postfix = rax_malloc(nodesize);
}
/* OOM? Abort now that the tree is untouched. */
if (splitnode == NULL ||
(trimmedlen && trimmed == NULL) ||
(postfixlen && postfix == NULL))
{
rax_free(splitnode);
rax_free(trimmed);
rax_free(postfix);
errno = ENOMEM;
return 0;
}
splitnode->data[0] = h->data[j];
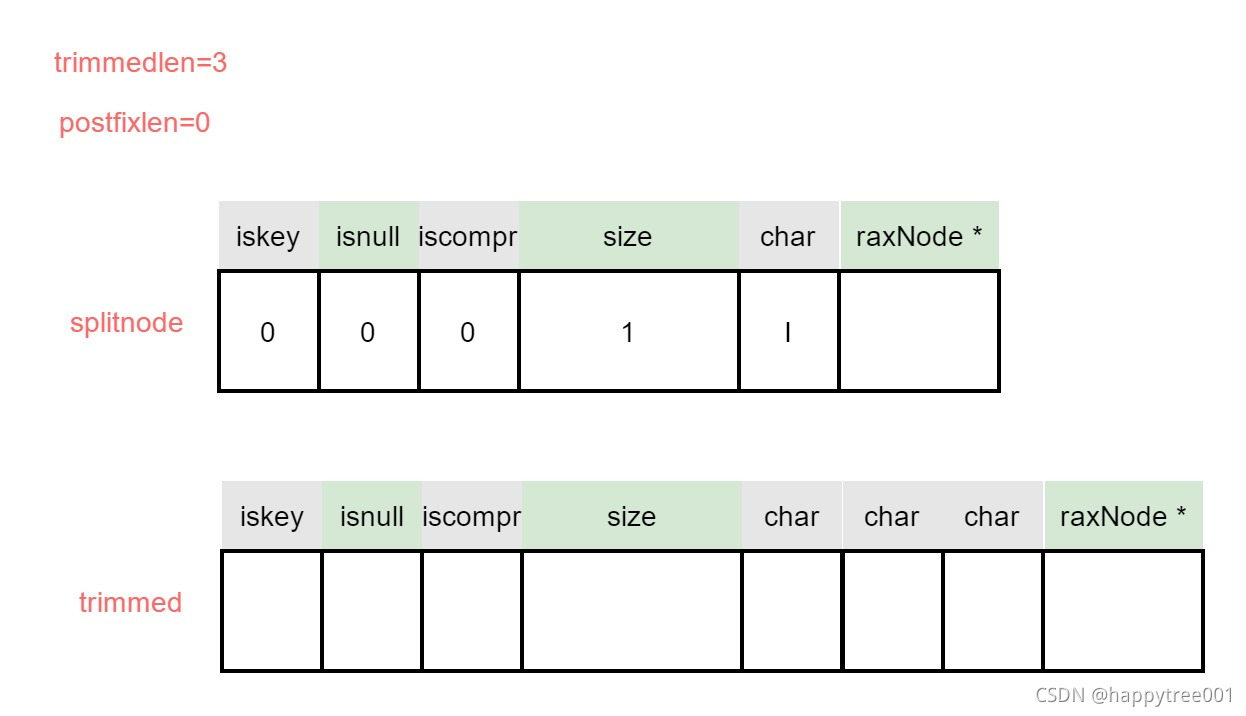
3.4.3.2.3 处理压缩节点前半部分
if (j == 0) {
/* 3a: Replace the old node with the split node. */
if (h->iskey) {
void *ndata = raxGetData(h);
raxSetData(splitnode,ndata);
}
memcpy(parentlink,&splitnode,sizeof(splitnode));
} else {
/* 3b: Trim the compressed node. */
trimmed->size = j;
memcpy(trimmed->data,h->data,j);
trimmed->iscompr = j > 1 ? 1 : 0;
trimmed->iskey = h->iskey;
trimmed->isnull = h->isnull;
if (h->iskey && !h->isnull) {
void *ndata = raxGetData(h);
raxSetData(trimmed,ndata);
}
raxNode **cp = raxNodeLastChildPtr(trimmed);
memcpy(cp,&splitnode,sizeof(splitnode));
memcpy(parentlink,&trimmed,sizeof(trimmed));
parentlink = cp; /* Set parentlink to splitnode parent. */
rax->numnodes++;
}
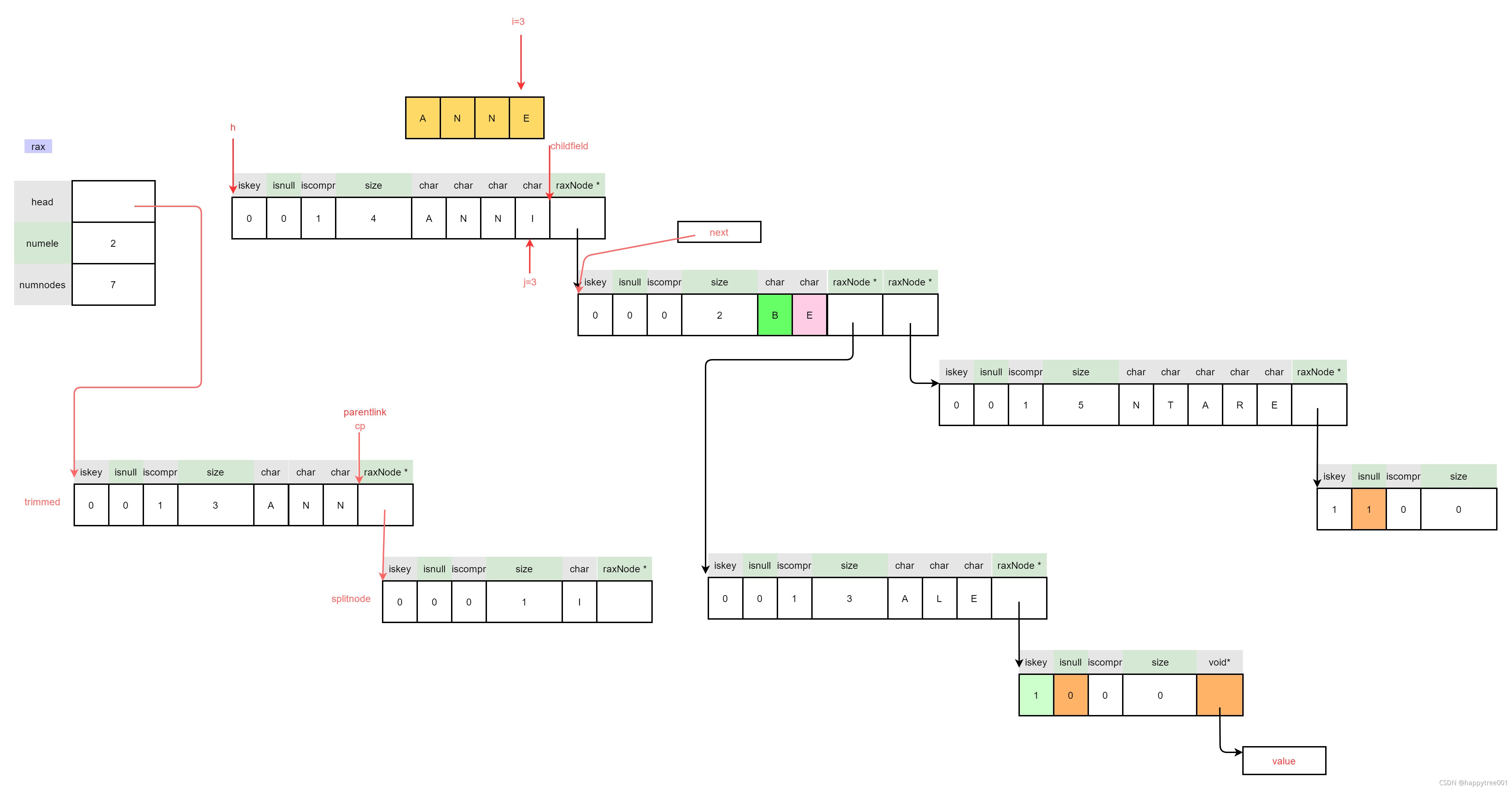
3.4.3.2.4 处理后半部分
/* 4: Create the postfix node: what remains of the original
* compressed node after the split. */
if (postfixlen) {
/* 4a: create a postfix node. */
postfix->iskey = 0;
postfix->isnull = 0;
postfix->size = postfixlen;
postfix->iscompr = postfixlen > 1;
memcpy(postfix->data,h->data+j+1,postfixlen);
raxNode **cp = raxNodeLastChildPtr(postfix);
memcpy(cp,&next,sizeof(next));
rax->numnodes++;
} else {
/* 4b: just use next as postfix node. */
postfix = next;
}
因postfixlen=0, 所以只是执行了简单的posfix=next
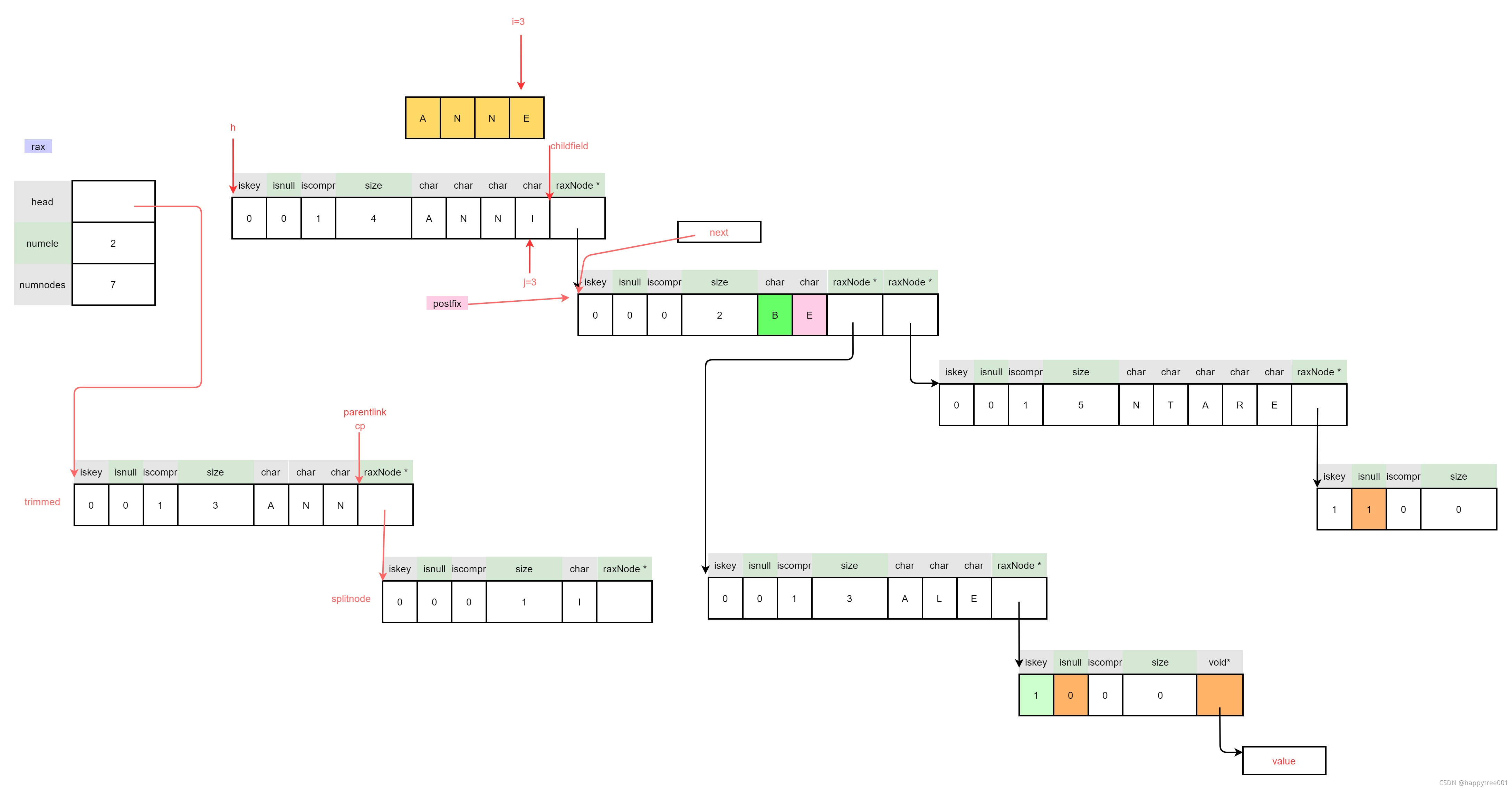
3.4.3.2.5 连接拆分节点
/* 5: Set splitnode first child as the postfix node. */
raxNode **splitchild = raxNodeLastChildPtr(splitnode);
memcpy(splitchild,&postfix,sizeof(postfix));
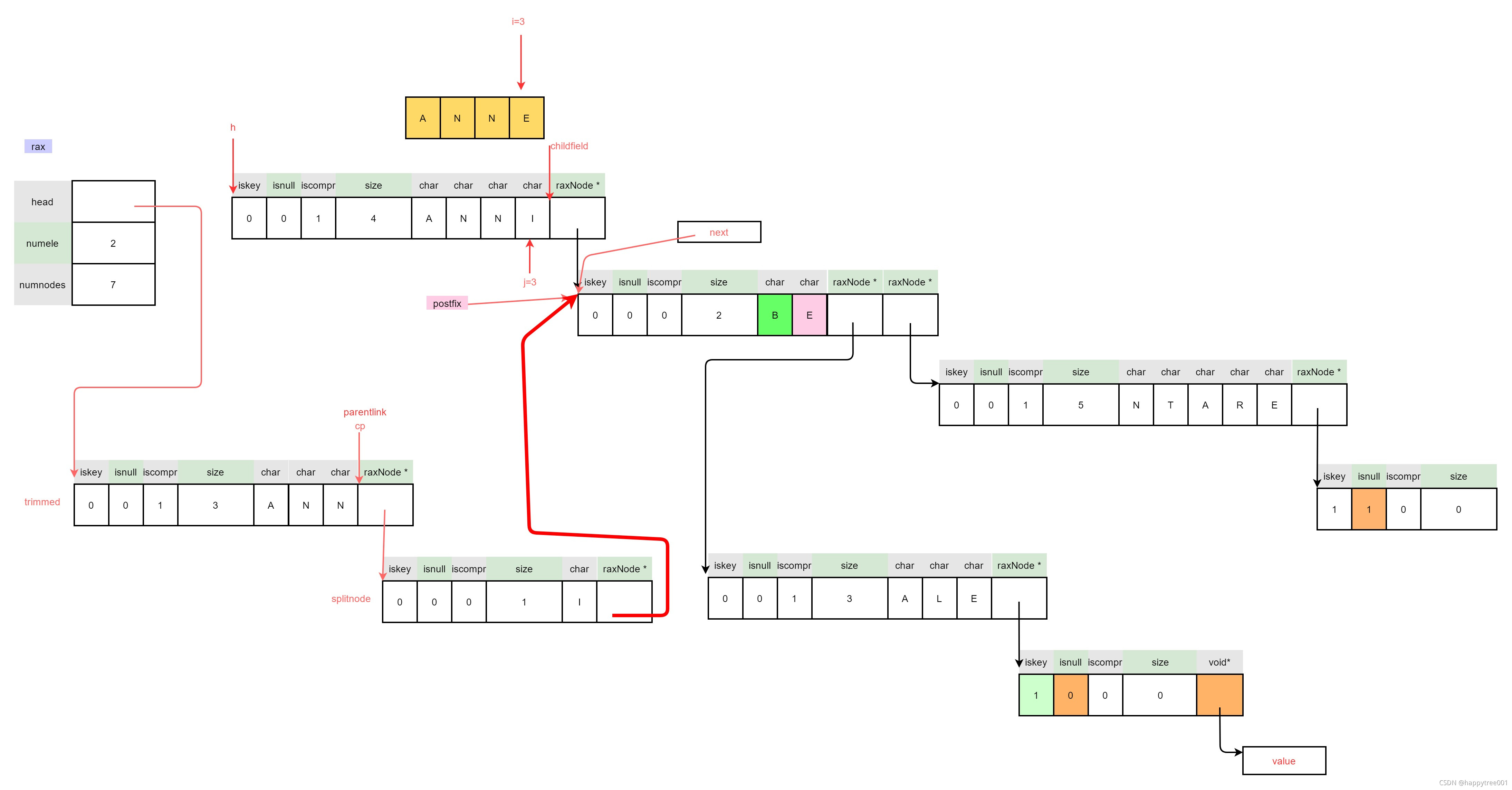
3.4.3.2.6 释放被拆分节点
/* 6. Continue insertion: this will cause the splitnode to
* get a new child (the non common character at the currently
* inserted key). */
rax_free(h);
h = splitnode;
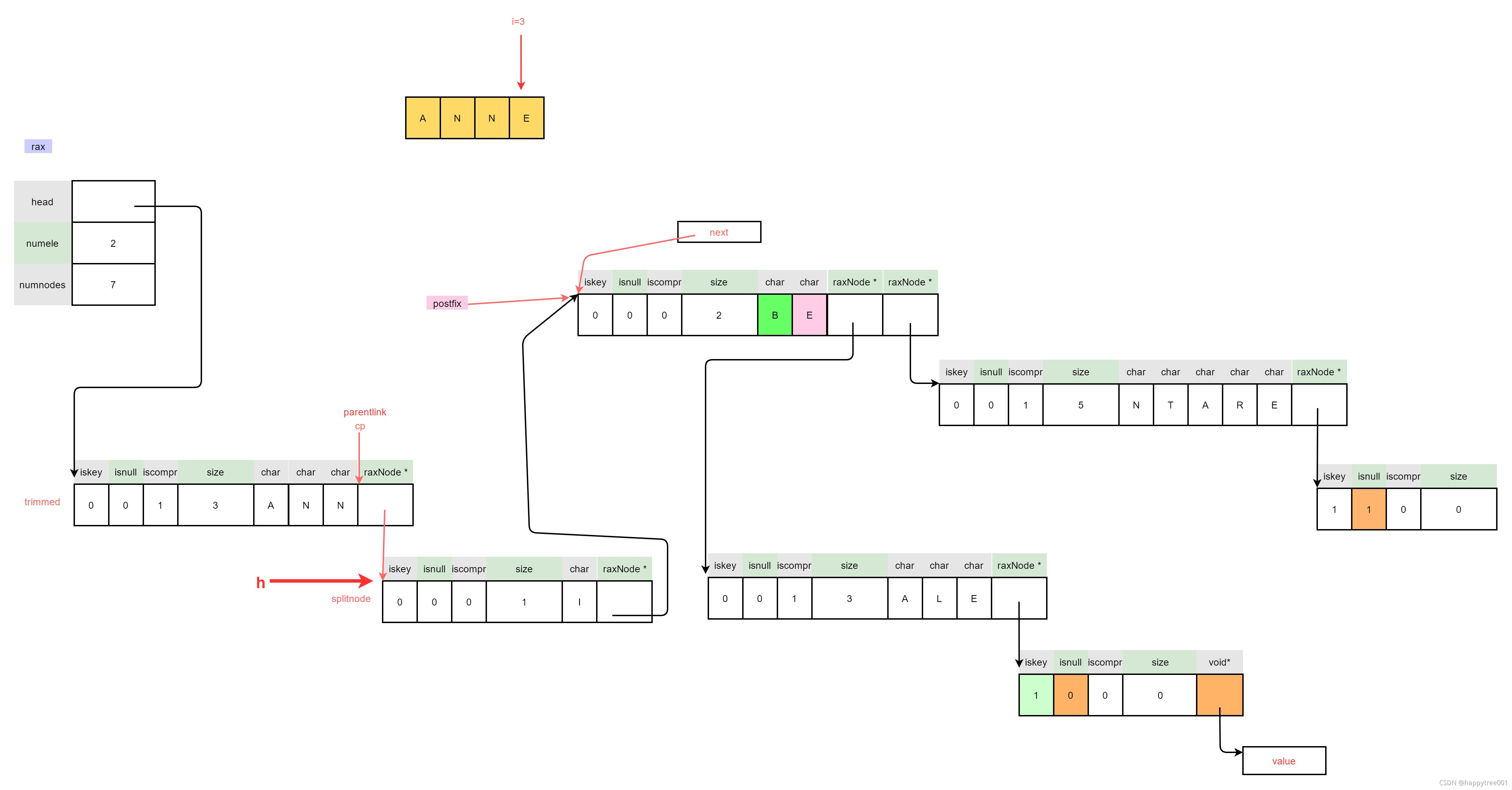
3.4.3.3 处理后续数据
3.4.3.3.1 处理剩余数据
没有剩余数据
3.4.3.3.2 插入value
- 扩容,用于存储value,本例子中data为null,不需要分配空间
raxNode *newh = raxReallocForData(h,data);
if (newh == NULL) goto oom;
h = newh;
- 增加元素个数
if (!h->iskey) rax->numele++;
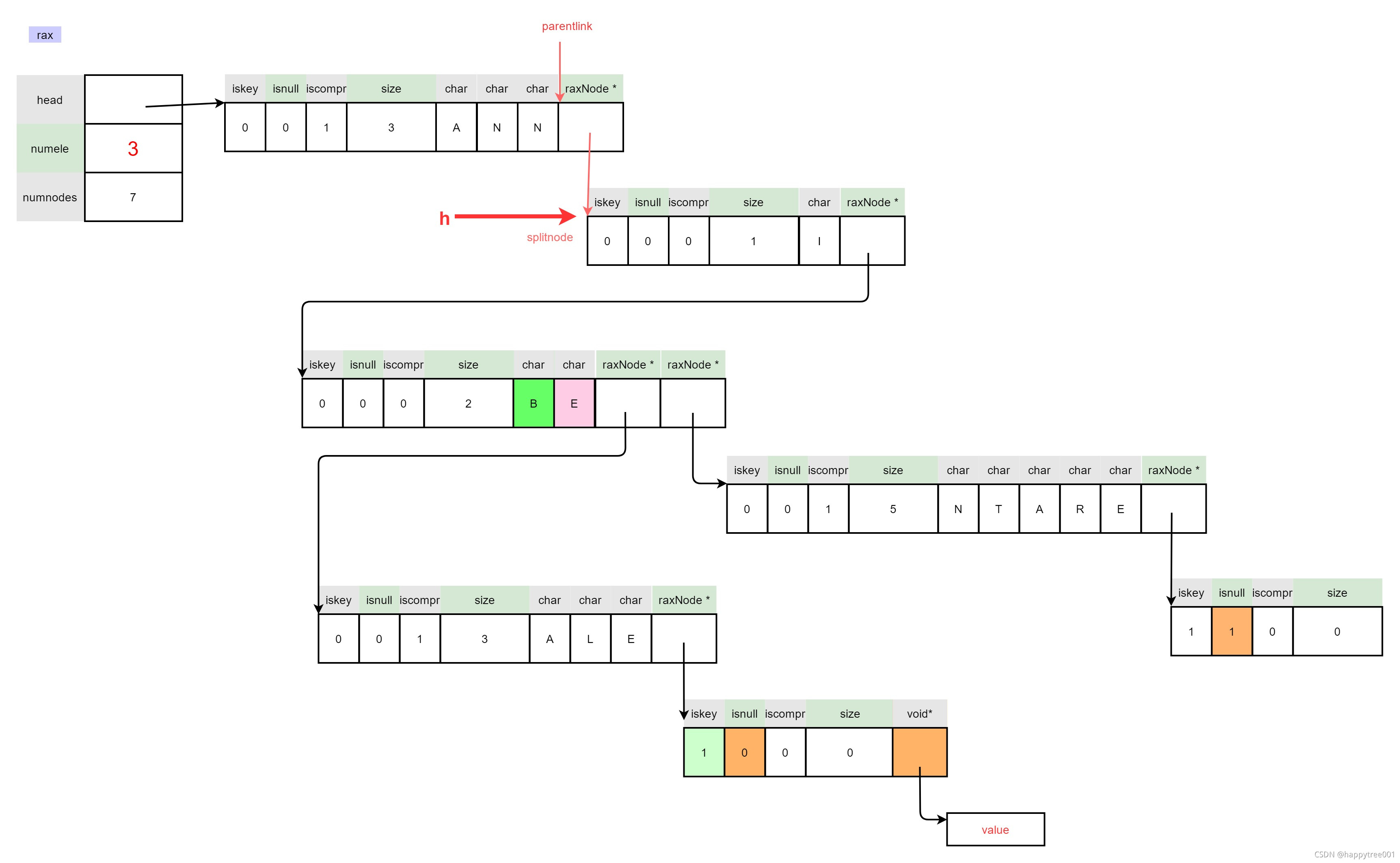
- 设置值
raxSetData(h,data);
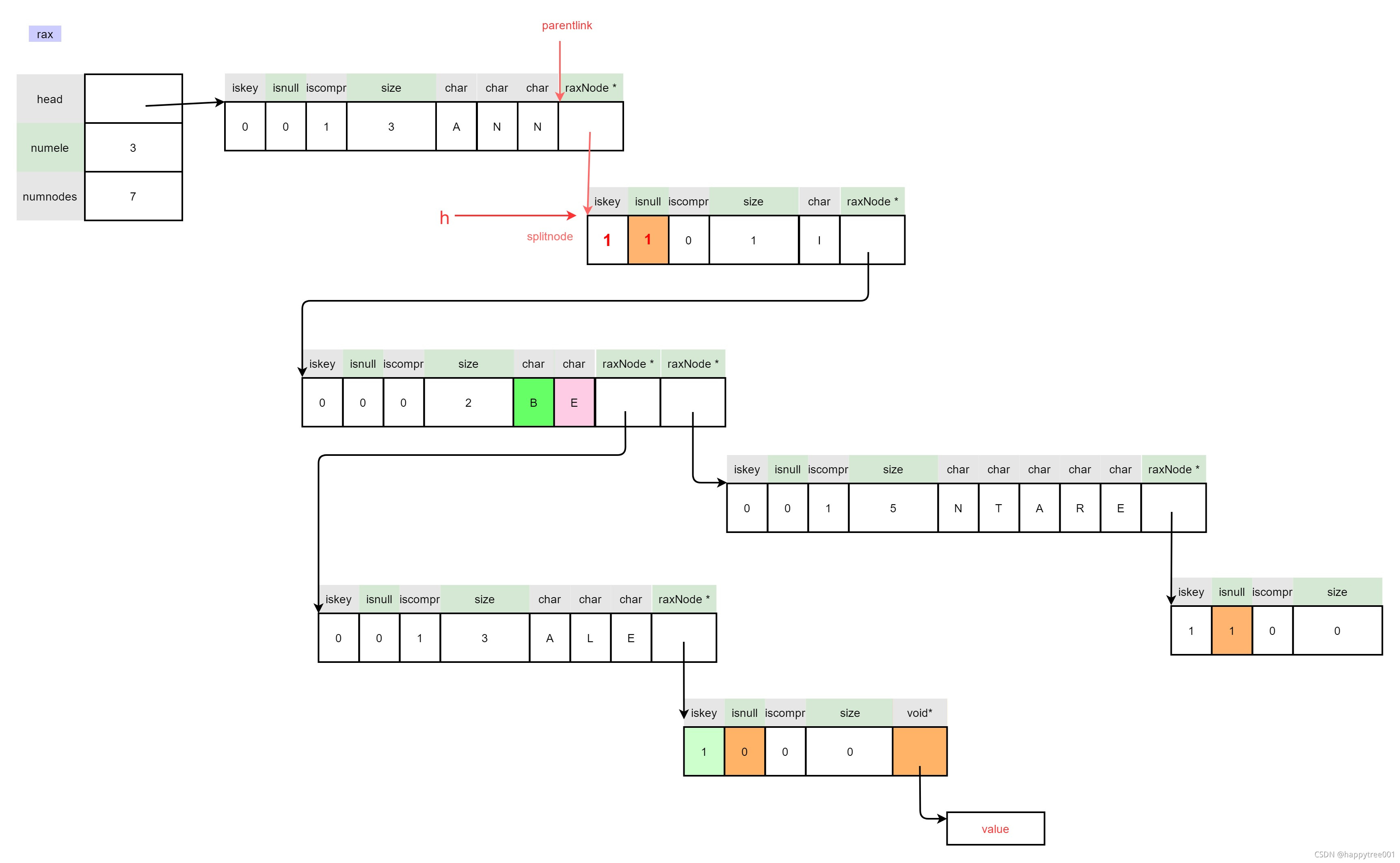
- 重新赋值连接
因为前面扩容重新分配空间,可能导致h地址改变,所以需要重新设置连接
memcpy(parentlink,&h,sizeof(h));
return 1; /* Element inserted. */
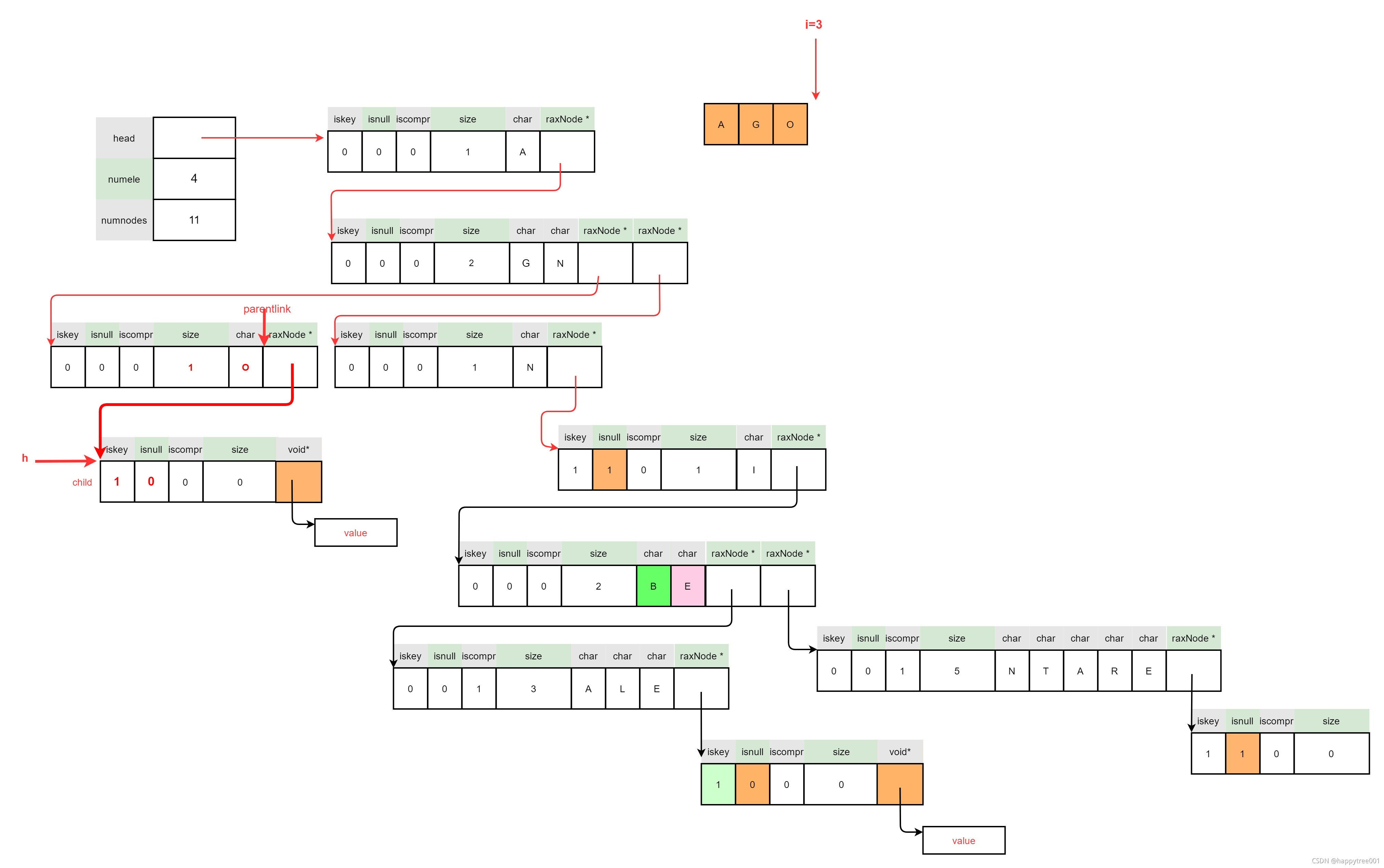
3.4.4 插入 “AGO”
char *data = malloc(100);
strcpy(data, "this is test!");
raxInsert(rax, "AGO", 3, data, NULL) ;
3.4.4.1 定位插入位置
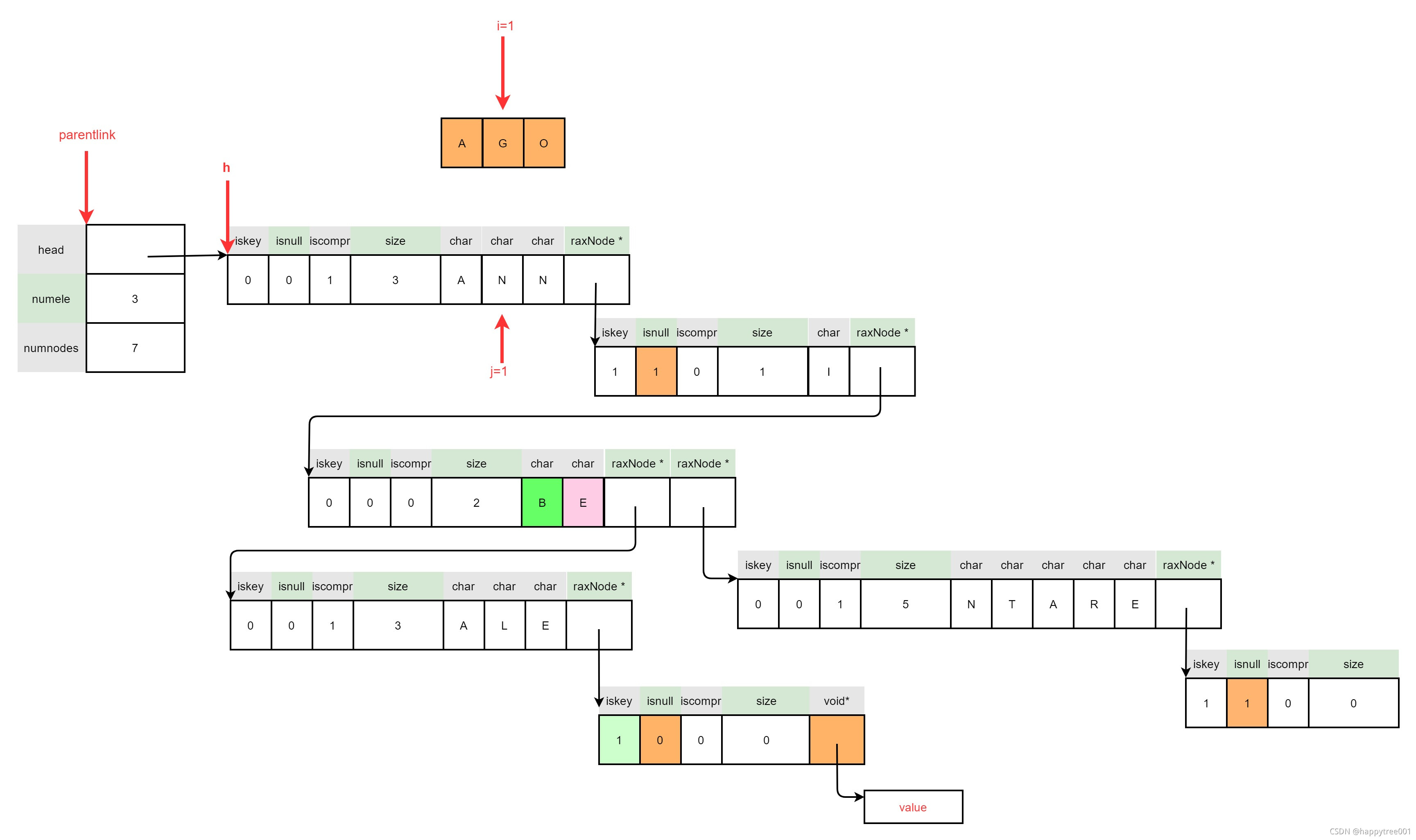
3.4.4.2 插入节点为压缩节点
3.4.4.2.1 保存next指针
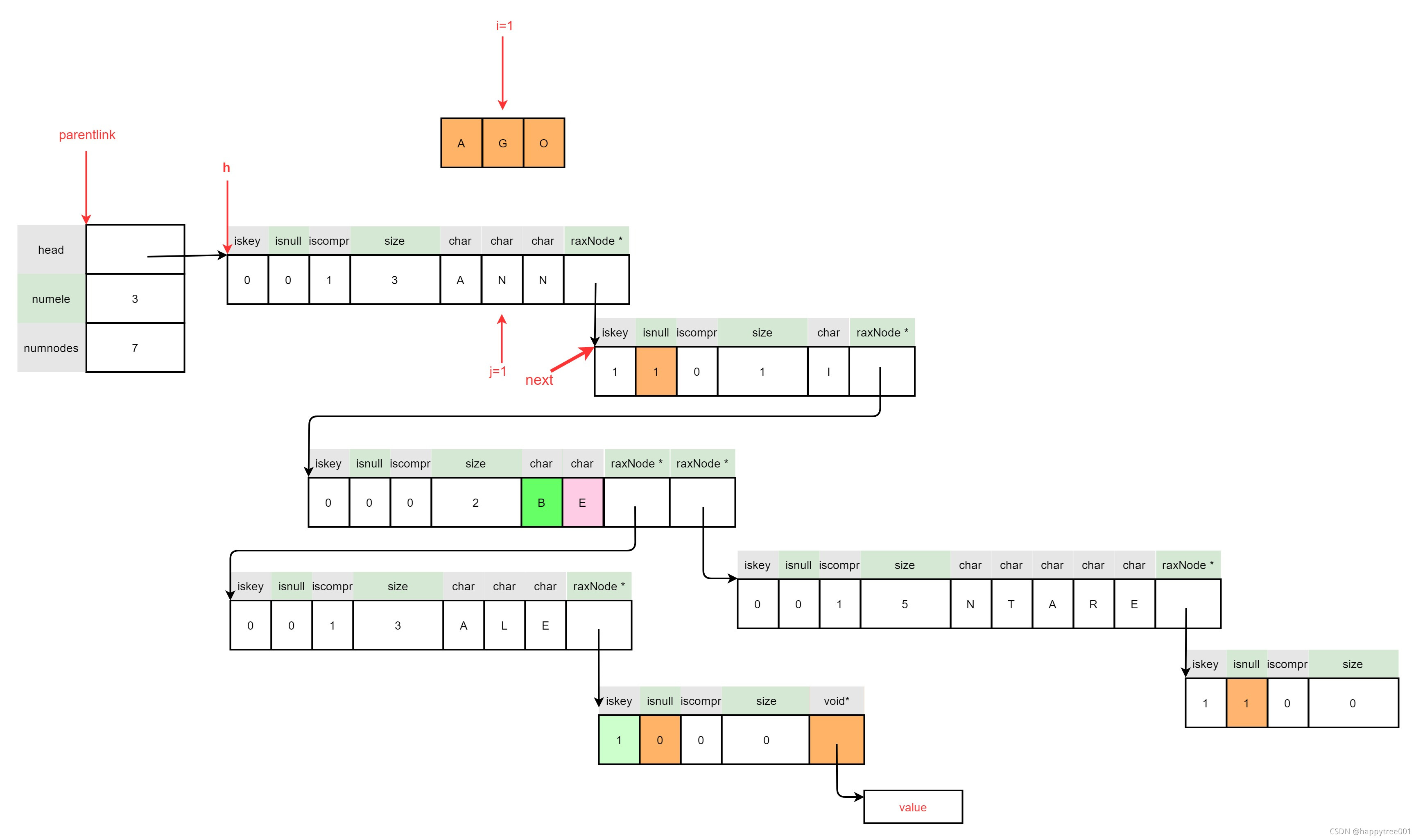
3.4.4.2.2 创建拆分节点
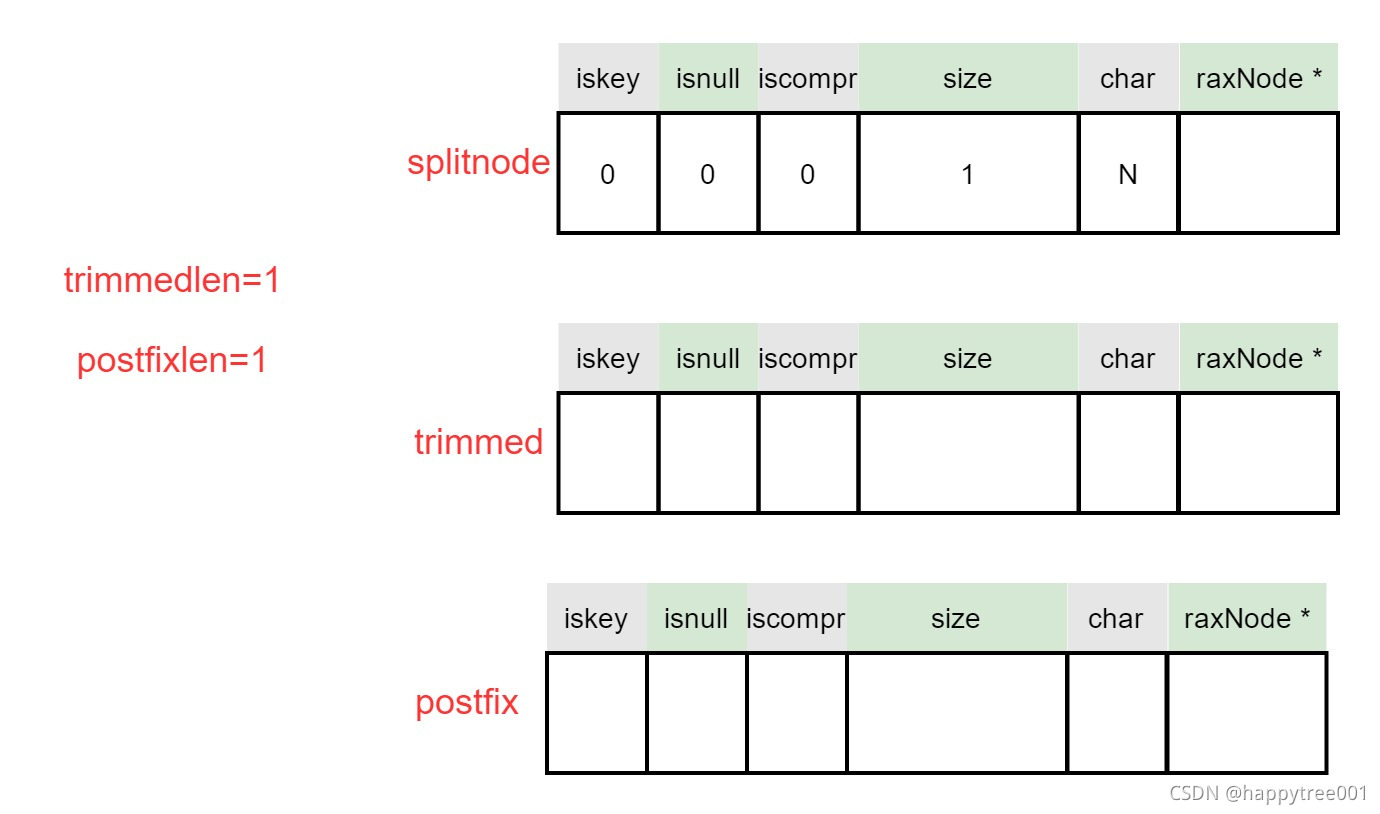
3.4.4.2.3 处理压缩节点前半部分
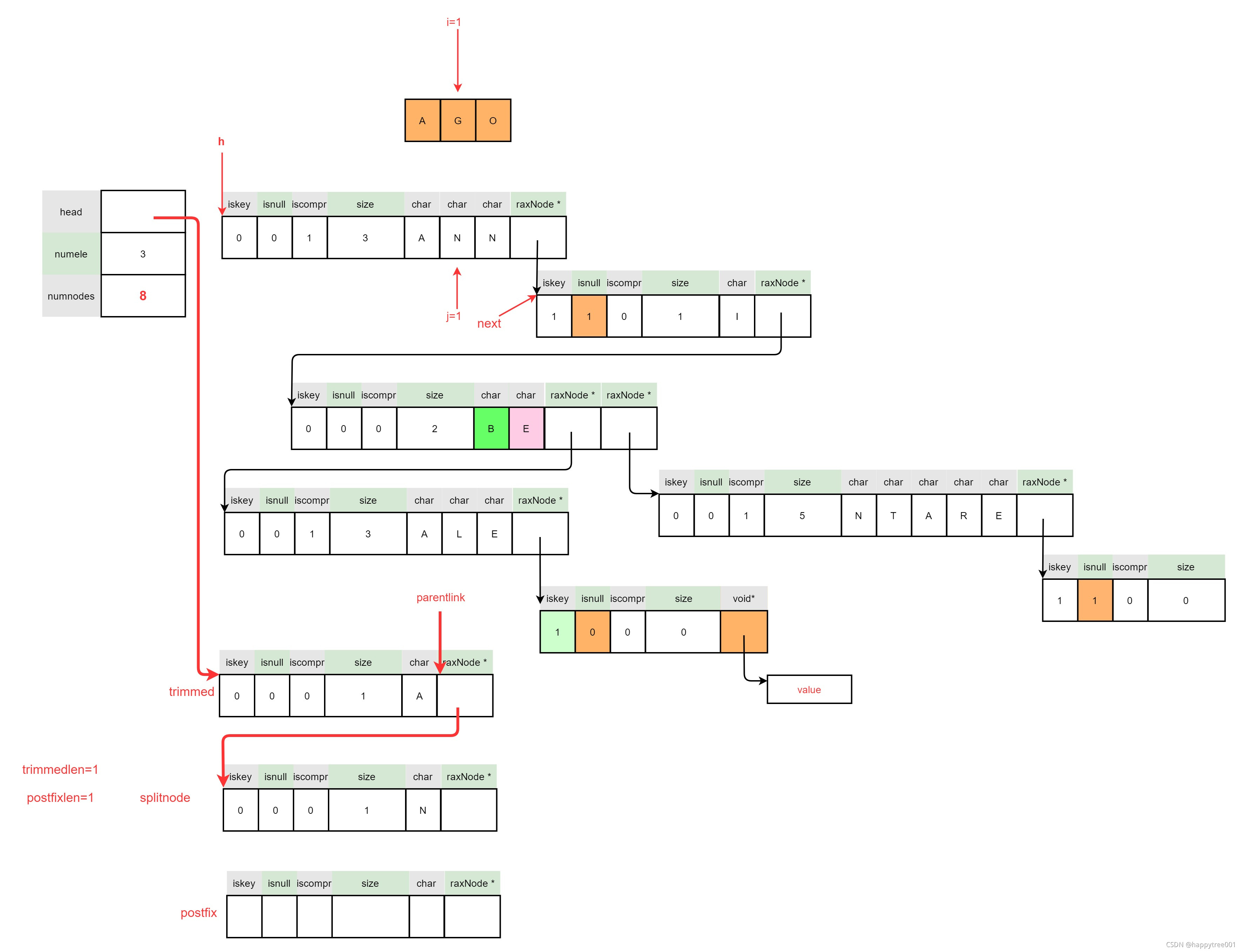
3.4.4.2.4 处理压缩节点后半部分
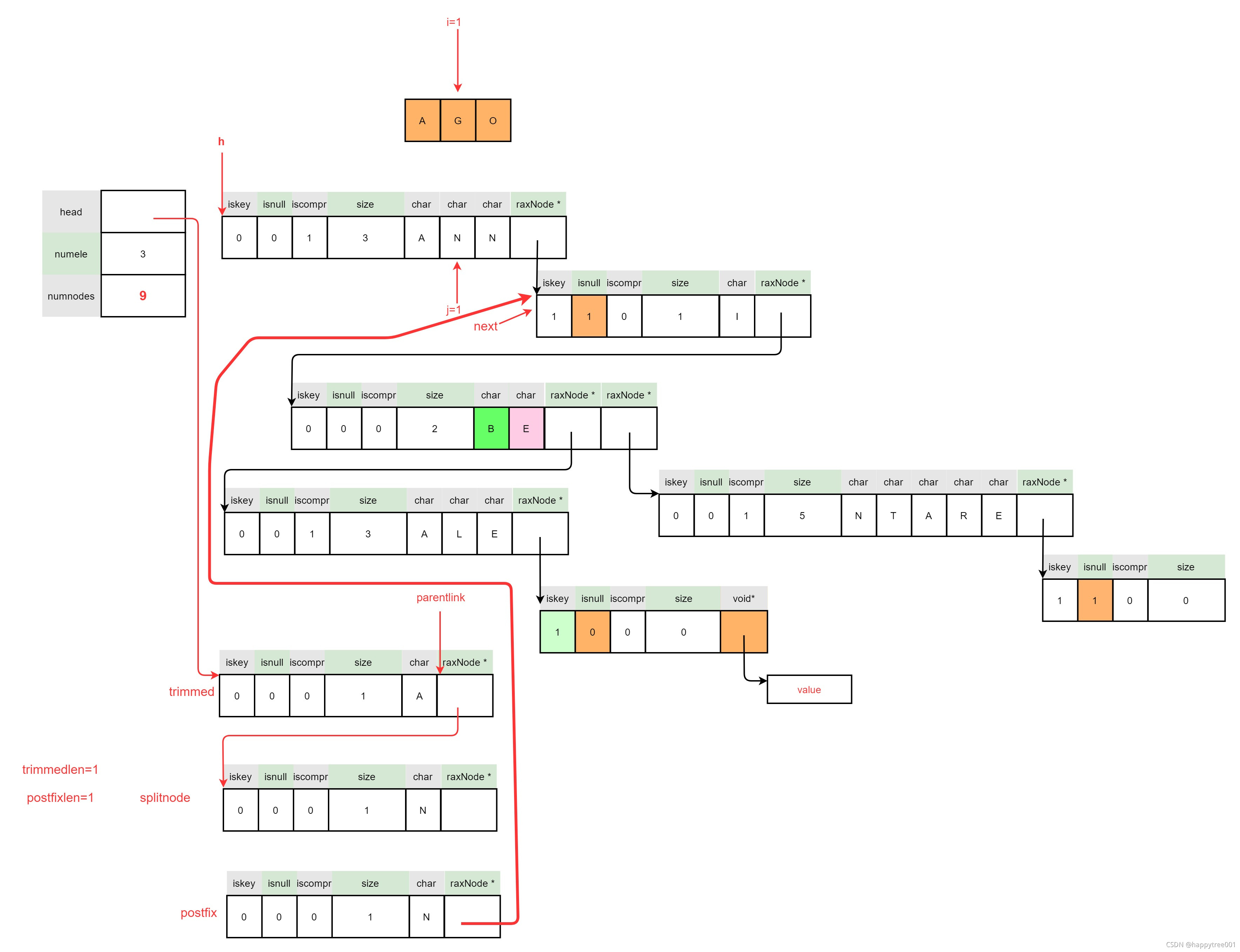
3.4.4.3.5 连接拆分节点
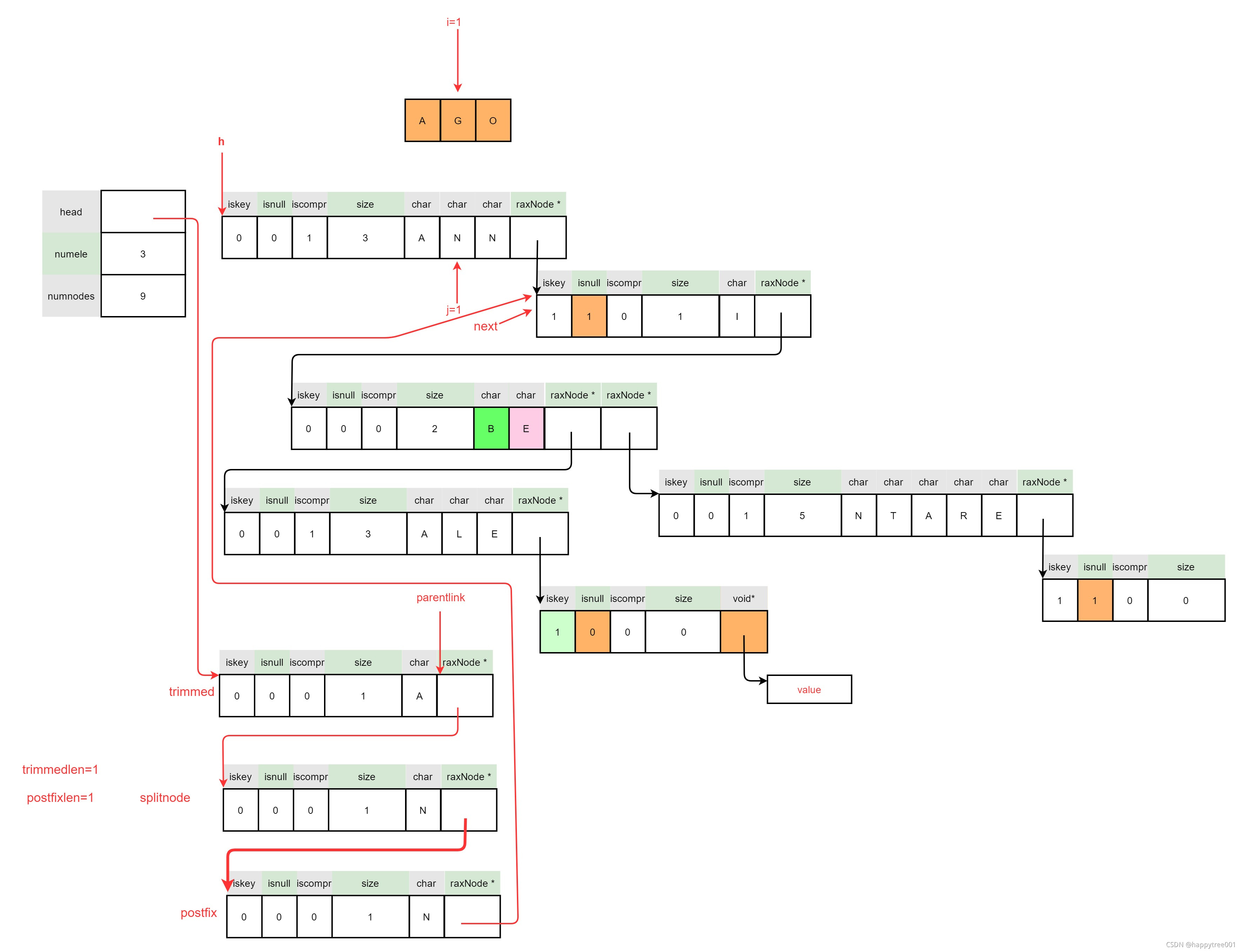
3.4.4.3.6 释放被拆分节点
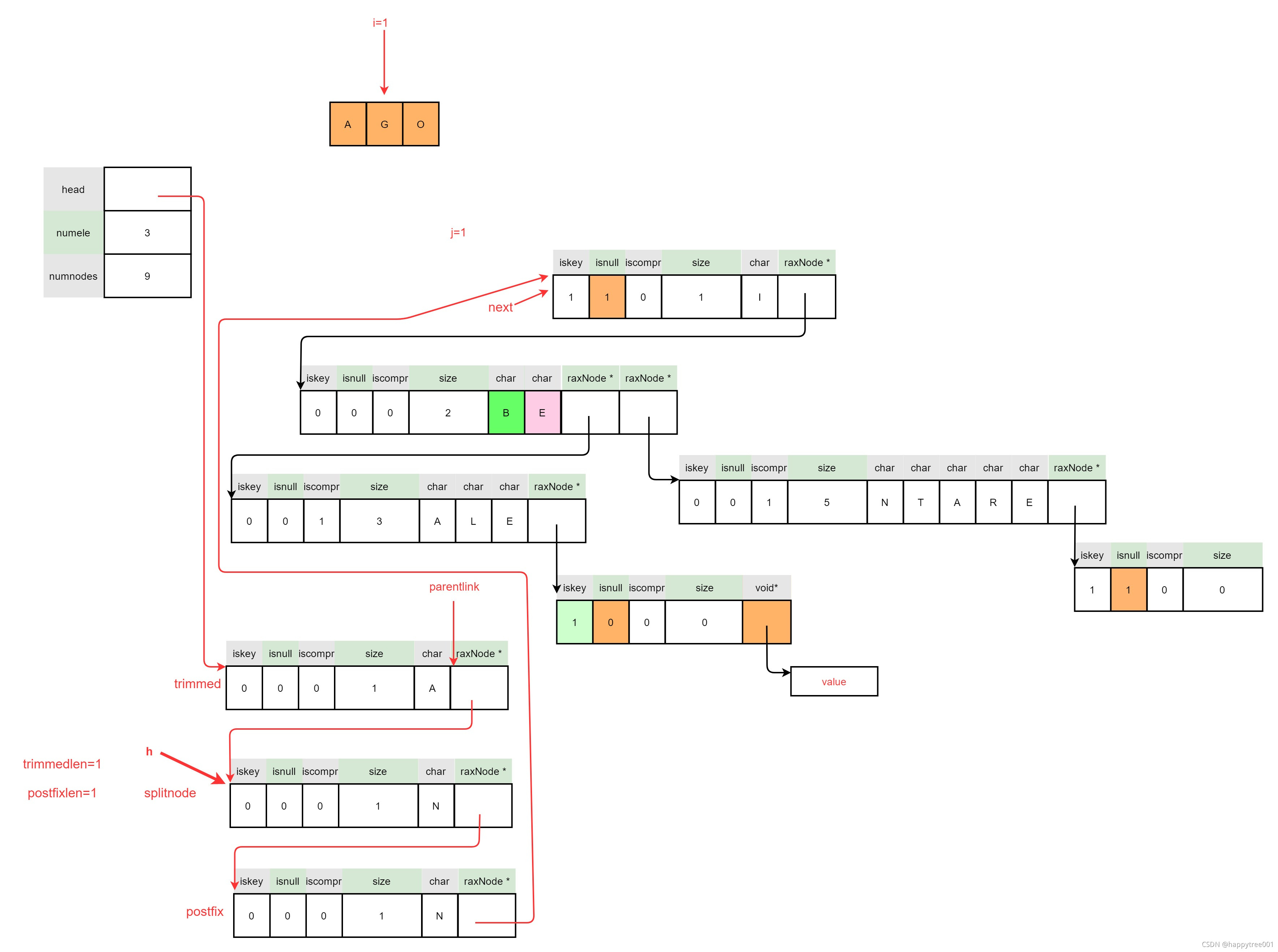
3.4.4.3 处理后续数据
3.4.4.3.1 处理剩余数据
- 插入正常节点
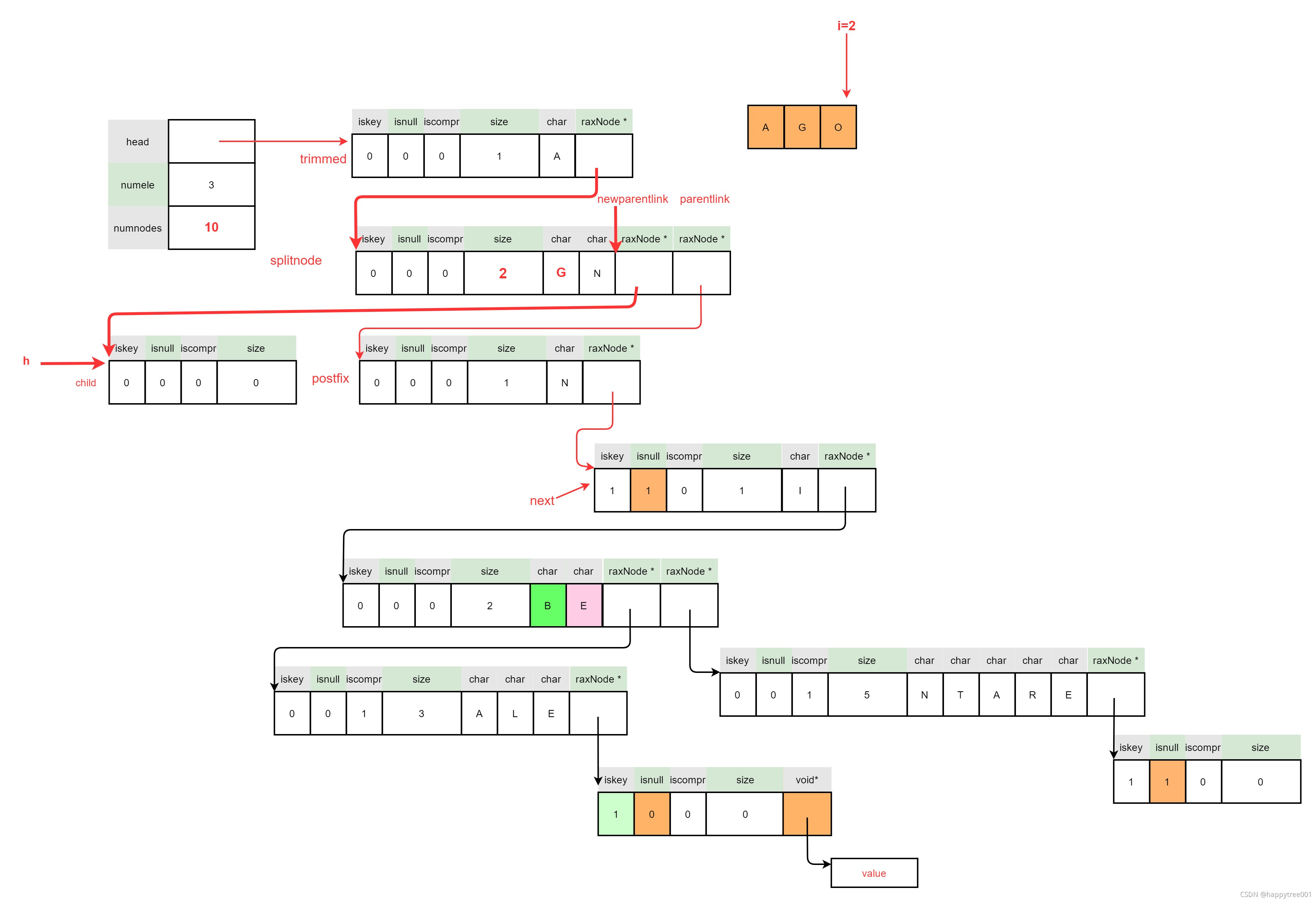
- 插入正常节点
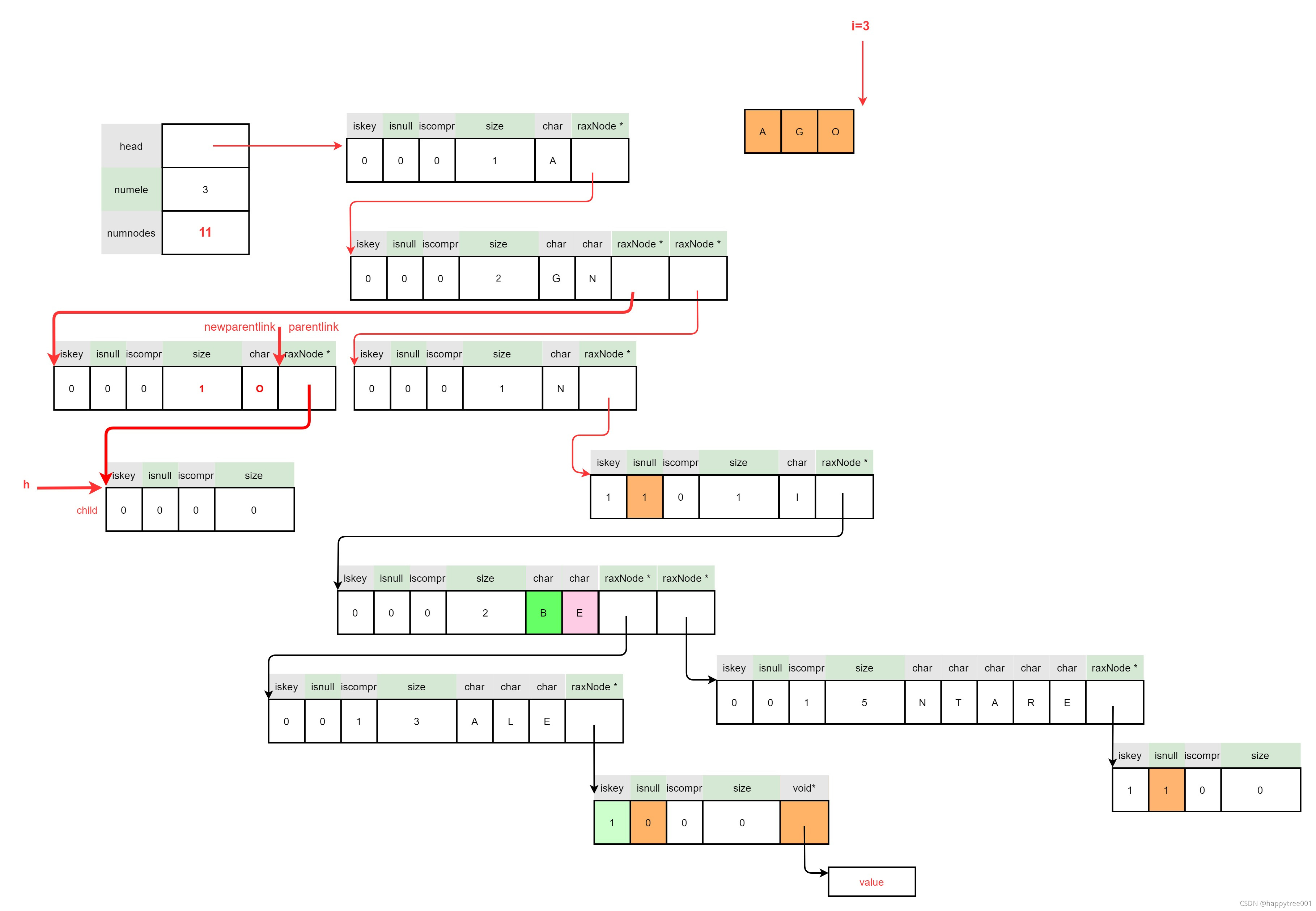
3.4.4.3.2 插入value
-
扩容
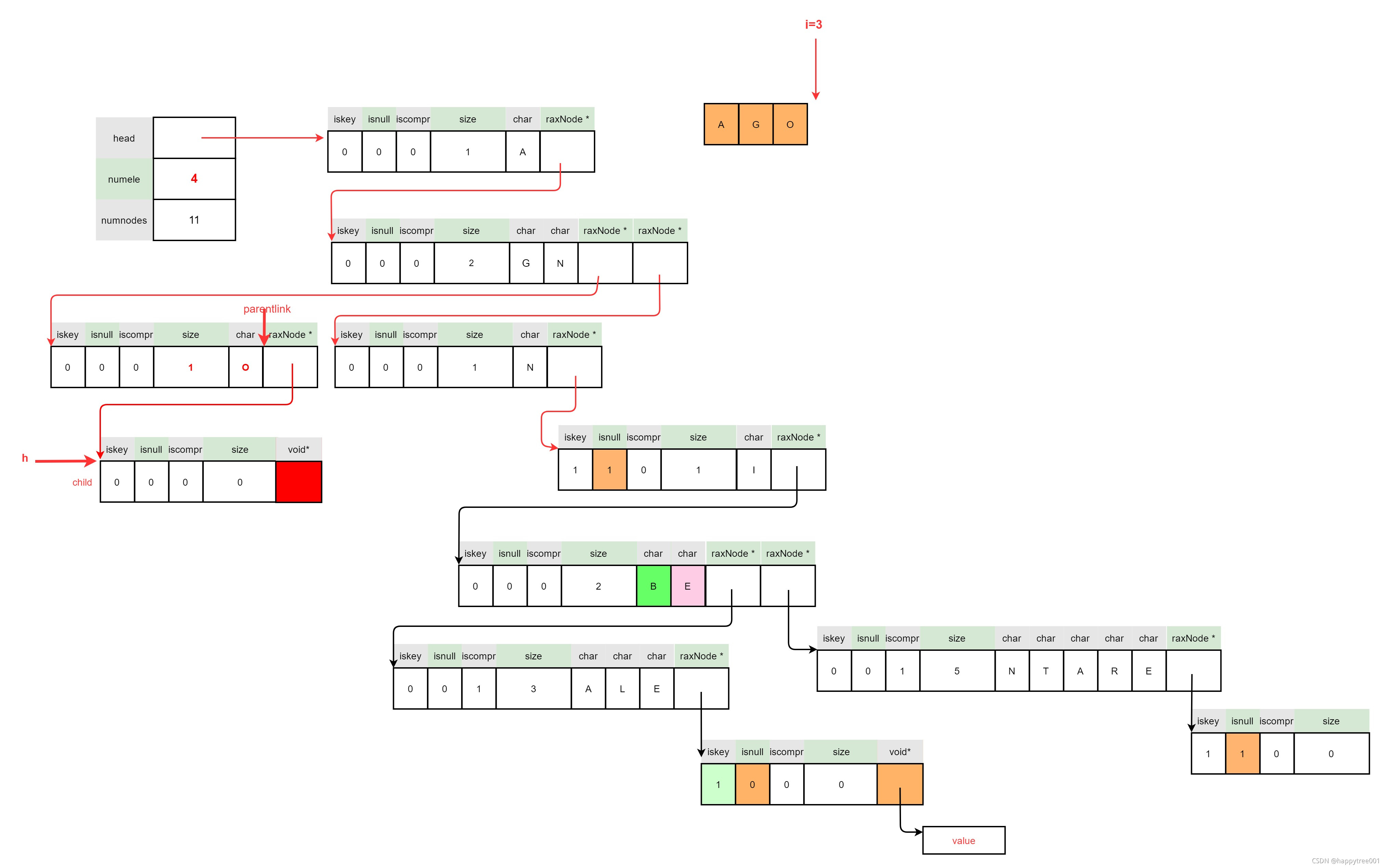
-
设置值
删除
相对于插入,在删除第一步查找过程中,会将经历过的节点加入栈中,后续循环处理,并且因节点的删除,某些节点需要合并成压缩节点。
/* Remove the specified item. Returns 1 if the item was found and
* deleted, 0 otherwise. */
int raxRemove(rax *rax, unsigned char *s, size_t len, void **old) {
raxNode *h;
raxStack ts;
debugf("### Delete: %.*s\n", (int)len, s);
raxStackInit(&ts);
int splitpos = 0;
size_t i = raxLowWalk(rax,s,len,&h,NULL,&splitpos,&ts);
if (i != len || (h->iscompr && splitpos != 0) || !h->iskey) {
raxStackFree(&ts);
return 0;
}
if (old) *old = raxGetData(h);
h->iskey = 0;
rax->numele--;
/* If this node has no children, the deletion needs to reclaim the
* no longer used nodes. This is an iterative process that needs to
* walk the three upward, deleting all the nodes with just one child
* that are not keys, until the head of the rax is reached or the first
* node with more than one child is found. */
int trycompress = 0; /* Will be set to 1 if we should try to optimize the
tree resulting from the deletion. */
if (h->size == 0) {
debugf("Key deleted in node without children. Cleanup needed.\n");
raxNode *child = NULL;
while(h != rax->head) {
child = h;
debugf("Freeing child %p [%.*s] key:%d\n", (void*)child,
(int)child->size, (char*)child->data, child->iskey);
rax_free(child);
rax->numnodes--;
h = raxStackPop(&ts);
/* If this node has more then one child, or actually holds
* a key, stop here. */
if (h->iskey || (!h->iscompr && h->size != 1)) break;
}
if (child) {
debugf("Unlinking child %p from parent %p\n",
(void*)child, (void*)h);
raxNode *new = raxRemoveChild(h,child);
if (new != h) {
raxNode *parent = raxStackPeek(&ts);
raxNode **parentlink;
if (parent == NULL) {
parentlink = &rax->head;
} else {
parentlink = raxFindParentLink(parent,h);
}
memcpy(parentlink,&new,sizeof(new));
}
/* If after the removal the node has just a single child
* and is not a key, we need to try to compress it. */
if (new->size == 1 && new->iskey == 0) {
trycompress = 1;
h = new;
}
}
} else if (h->size == 1) {
/* If the node had just one child, after the removal of the key
* further compression with adjacent nodes is pontentially possible. */
trycompress = 1;
}
/* Don't try node compression if our nodes pointers stack is not
* complete because of OOM while executing raxLowWalk() */
if (trycompress && ts.oom) trycompress = 0;
/* Recompression: if trycompress is true, 'h' points to a radix tree node
* that changed in a way that could allow to compress nodes in this
* sub-branch. Compressed nodes represent chains of nodes that are not
* keys and have a single child, so there are two deletion events that
* may alter the tree so that further compression is needed:
*
* 1) A node with a single child was a key and now no longer is a key.
* 2) A node with two children now has just one child.
*
* We try to navigate upward till there are other nodes that can be
* compressed, when we reach the upper node which is not a key and has
* a single child, we scan the chain of children to collect the
* compressable part of the tree, and replace the current node with the
* new one, fixing the child pointer to reference the first non
* compressable node.
*
* Example of case "1". A tree stores the keys "FOO" = 1 and
* "FOOBAR" = 2:
*
*
* "FOO" -> "BAR" -> [] (2)
* (1)
*
* After the removal of "FOO" the tree can be compressed as:
*
* "FOOBAR" -> [] (2)
*
*
* Example of case "2". A tree stores the keys "FOOBAR" = 1 and
* "FOOTER" = 2:
*
* |B| -> "AR" -> [] (1)
* "FOO" -> |-|
* |T| -> "ER" -> [] (2)
*
* After the removal of "FOOTER" the resulting tree is:
*
* "FOO" -> |B| -> "AR" -> [] (1)
*
* That can be compressed into:
*
* "FOOBAR" -> [] (1)
*/
if (trycompress) {
debugf("After removing %.*s:\n", (int)len, s);
debugnode("Compression may be needed",h);
debugf("Seek start node\n");
/* Try to reach the upper node that is compressible.
* At the end of the loop 'h' will point to the first node we
* can try to compress and 'parent' to its parent. */
raxNode *parent;
while(1) {
parent = raxStackPop(&ts);
if (!parent || parent->iskey ||
(!parent->iscompr && parent->size != 1)) break;
h = parent;
debugnode("Going up to",h);
}
raxNode *start = h; /* Compression starting node. */
/* Scan chain of nodes we can compress. */
size_t comprsize = h->size;
int nodes = 1;
while(h->size != 0) {
raxNode **cp = raxNodeLastChildPtr(h);
memcpy(&h,cp,sizeof(h));
if (h->iskey || (!h->iscompr && h->size != 1)) break;
/* Stop here if going to the next node would result into
* a compressed node larger than h->size can hold. */
if (comprsize + h->size > RAX_NODE_MAX_SIZE) break;
nodes++;
comprsize += h->size;
}
if (nodes > 1) {
/* If we can compress, create the new node and populate it. */
size_t nodesize =
sizeof(raxNode)+comprsize+sizeof(raxNode*);
raxNode *new = rax_malloc(nodesize);
/* An out of memory here just means we cannot optimize this
* node, but the tree is left in a consistent state. */
if (new == NULL) {
raxStackFree(&ts);
return 1;
}
new->iskey = 0;
new->isnull = 0;
new->iscompr = 1;
new->size = comprsize;
rax->numnodes++;
/* Scan again, this time to populate the new node content and
* to fix the new node child pointer. At the same time we free
* all the nodes that we'll no longer use. */
comprsize = 0;
h = start;
while(h->size != 0) {
memcpy(new->data+comprsize,h->data,h->size);
comprsize += h->size;
raxNode **cp = raxNodeLastChildPtr(h);
raxNode *tofree = h;
memcpy(&h,cp,sizeof(h));
rax_free(tofree); rax->numnodes--;
if (h->iskey || (!h->iscompr && h->size != 1)) break;
}
debugnode("New node",new);
/* Now 'h' points to the first node that we still need to use,
* so our new node child pointer will point to it. */
raxNode **cp = raxNodeLastChildPtr(new);
memcpy(cp,&h,sizeof(h));
/* Fix parent link. */
if (parent) {
raxNode **parentlink = raxFindParentLink(parent,start);
memcpy(parentlink,&new,sizeof(new));
} else {
rax->head = new;
}
debugf("Compressed %d nodes, %d total bytes\n",
nodes, (int)comprsize);
}
}
raxStackFree(&ts);
return 1;
}
3.5.1 删除“ANNIENTARE”
raxRemove(rax, "ANNIENTARE", 10, NULL) {
3.5.1.1 初始化路径栈
raxStackInit(&ts);
static inline void raxStackInit(raxStack *ts) {
ts->stack = ts->static_items;
ts->items = 0;
ts->maxitems = RAX_STACK_STATIC_ITEMS;
ts->oom = 0;
}
栈结构内有一个静态的数组,当处理的个数小于32个时,避免频繁分配空间,当处理的个数大于32时,将动态的分配空间,并且扩容策略:大小翻倍
#define RAX_STACK_STATIC_ITEMS 32
typedef struct raxStack {
void **stack; /* Points to static_items or an heap allocated array. */
size_t items, maxitems; /* Number of items contained and total space. */
/* Up to RAXSTACK_STACK_ITEMS items we avoid to allocate on the heap
* and use this static array of pointers instead. */
void *static_items[RAX_STACK_STATIC_ITEMS];
int oom; /* True if pushing into this stack failed for OOM at some point. */
} raxStack;
3.5.1.2 查找删除key,并且记录搜索路径栈
size_t i = raxLowWalk(rax,s,len,&h,NULL,&splitpos,&ts);
if (i != len || (h->iscompr && splitpos != 0) || !h->iskey) {
raxStackFree(&ts);
return 0;
}
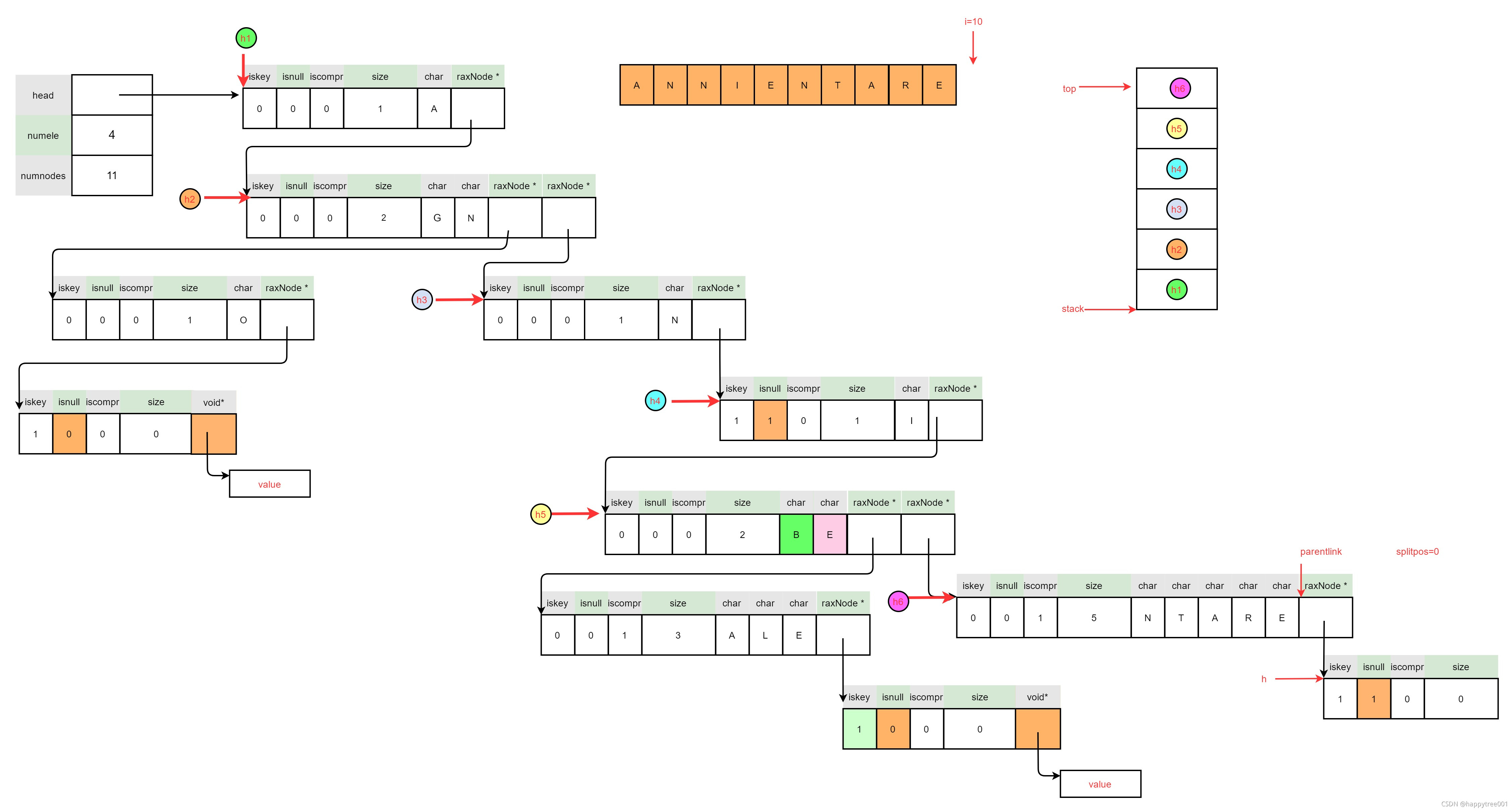
3.5.1.3 保存删除节点数据
if (old) *old = raxGetData(h);
3.5.1.4 减少元素个数
h->iskey = 0;
rax->numele--;
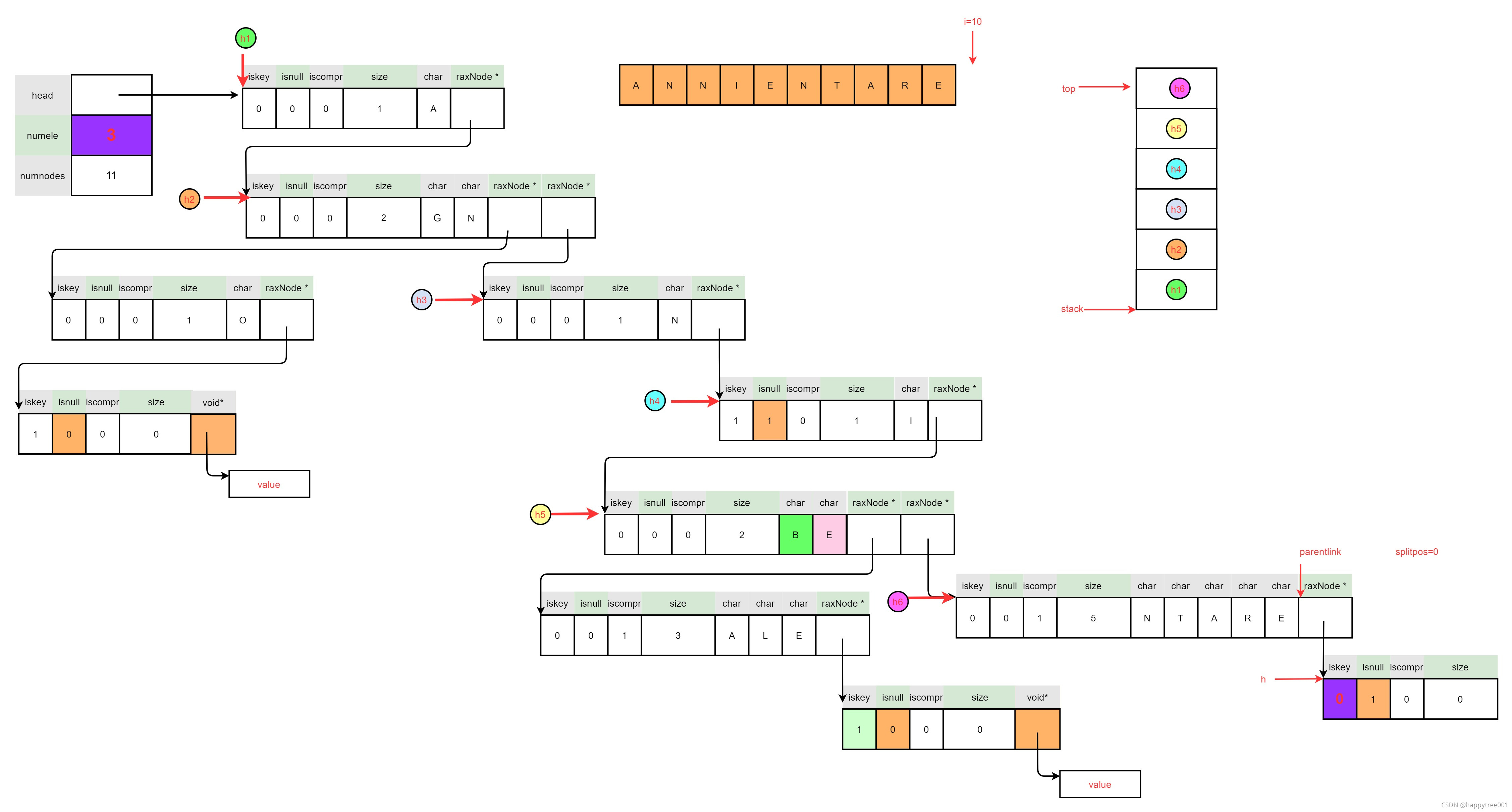
3.5.1.5 删除不在使用的节点
/* If this node has no children, the deletion needs to reclaim the
* no longer used nodes. This is an iterative process that needs to
* walk the three upward, deleting all the nodes with just one child
* that are not keys, until the head of the rax is reached or the first
* node with more than one child is found. */
int trycompress = 0; /* Will be set to 1 if we should try to optimize the
tree resulting from the deletion. */
if (h->size == 0) {
debugf("Key deleted in node without children. Cleanup needed.\n");
raxNode *child = NULL;
while(h != rax->head) {
child = h;
debugf("Freeing child %p [%.*s] key:%d\n", (void*)child,
(int)child->size, (char*)child->data, child->iskey);
rax_free(child);
rax->numnodes--;
h = raxStackPop(&ts);
/* If this node has more then one child, or actually holds
* a key, stop here. */
if (h->iskey || (!h->iscompr && h->size != 1)) break;
}
...
}
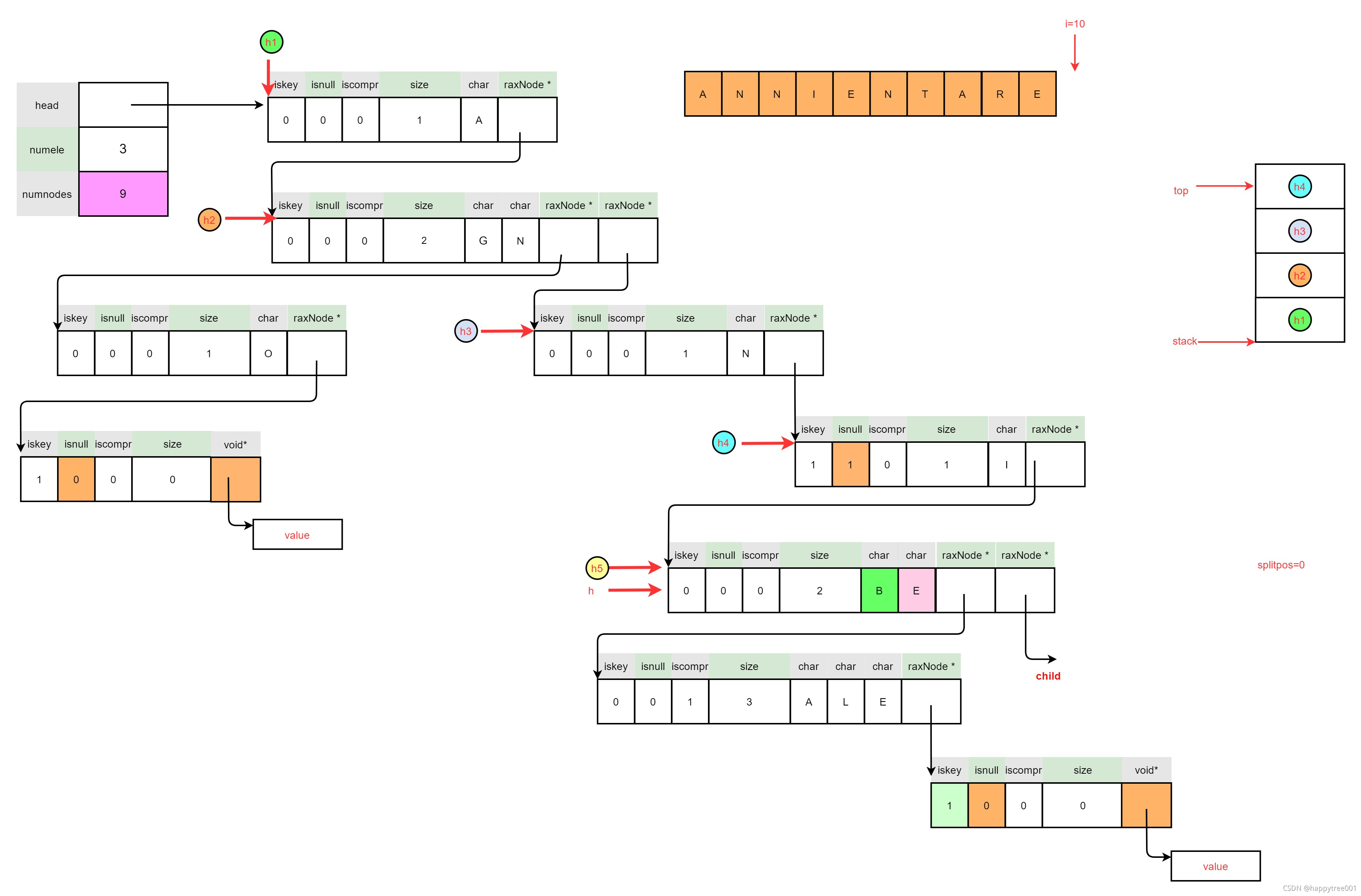
if (child) {
debugf("Unlinking child %p from parent %p\n",
(void*)child, (void*)h);
raxNode *new = raxRemoveChild(h,child);
if (new != h) {
raxNode *parent = raxStackPeek(&ts);
raxNode **parentlink;
if (parent == NULL) {
parentlink = &rax->head;
} else {
parentlink = raxFindParentLink(parent,h);
}
memcpy(parentlink,&new,sizeof(new));
}
/* If after the removal the node has just a single child
* and is not a key, we need to try to compress it. */
if (new->size == 1 && new->iskey == 0) {
trycompress = 1;
h = new;
}
}
/* Low level child removal from node. The new node pointer (after the child
* removal) is returned. Note that this function does not fix the pointer
* of the parent node in its parent, so this task is up to the caller.
* The function never fails for out of memory. */
raxNode *raxRemoveChild(raxNode *parent, raxNode *child) {
debugnode("raxRemoveChild before", parent);
/* If parent is a compressed node (having a single child, as for definition
* of the data structure), the removal of the child consists into turning
* it into a normal node without children. */
if (parent->iscompr) {
void *data = NULL;
if (parent->iskey) data = raxGetData(parent);
parent->isnull = 0;
parent->iscompr = 0;
parent->size = 0;
if (parent->iskey) raxSetData(parent,data);
debugnode("raxRemoveChild after", parent);
return parent;
}
/* Otherwise we need to scan for the children pointer and memmove()
* accordingly.
*
* 1. To start we seek the first element in both the children
* pointers and edge bytes in the node. */
raxNode **cp = raxNodeFirstChildPtr(parent);
raxNode **c = cp;
unsigned char *e = parent->data;
/* 2. Search the child pointer to remove inside the array of children
* pointers. */
while(1) {
raxNode *aux;
memcpy(&aux,c,sizeof(aux));
if (aux == child) break;
c++;
e++;
}
/* 3. Remove the edge and the pointer by memmoving the remaining children
* pointer and edge bytes one position before. */
int taillen = parent->size - (e - parent->data) - 1;
debugf("raxRemoveChild tail len: %d\n", taillen);
memmove(e,e+1,taillen);
/* Since we have one data byte less, also child pointers start one byte
* before now. */
memmove(((char*)cp)-1,cp,(parent->size-taillen-1)*sizeof(raxNode**));
/* Move the remaining "tail" pointer at the right position as well. */
memmove(((char*)c)-1,c+1,taillen*sizeof(raxNode**)+parent->iskey*sizeof(void*));
/* 4. Update size. */
parent->size--;
/* realloc the node according to the theoretical memory usage, to free
* data if we are over-allocating right now. */
raxNode *newnode = rax_realloc(parent,raxNodeCurrentLength(parent));
if (newnode) {
debugnode("raxRemoveChild after", newnode);
}
/* Note: if rax_realloc() fails we just return the old address, which
* is valid. */
return newnode ? newnode : parent;
}
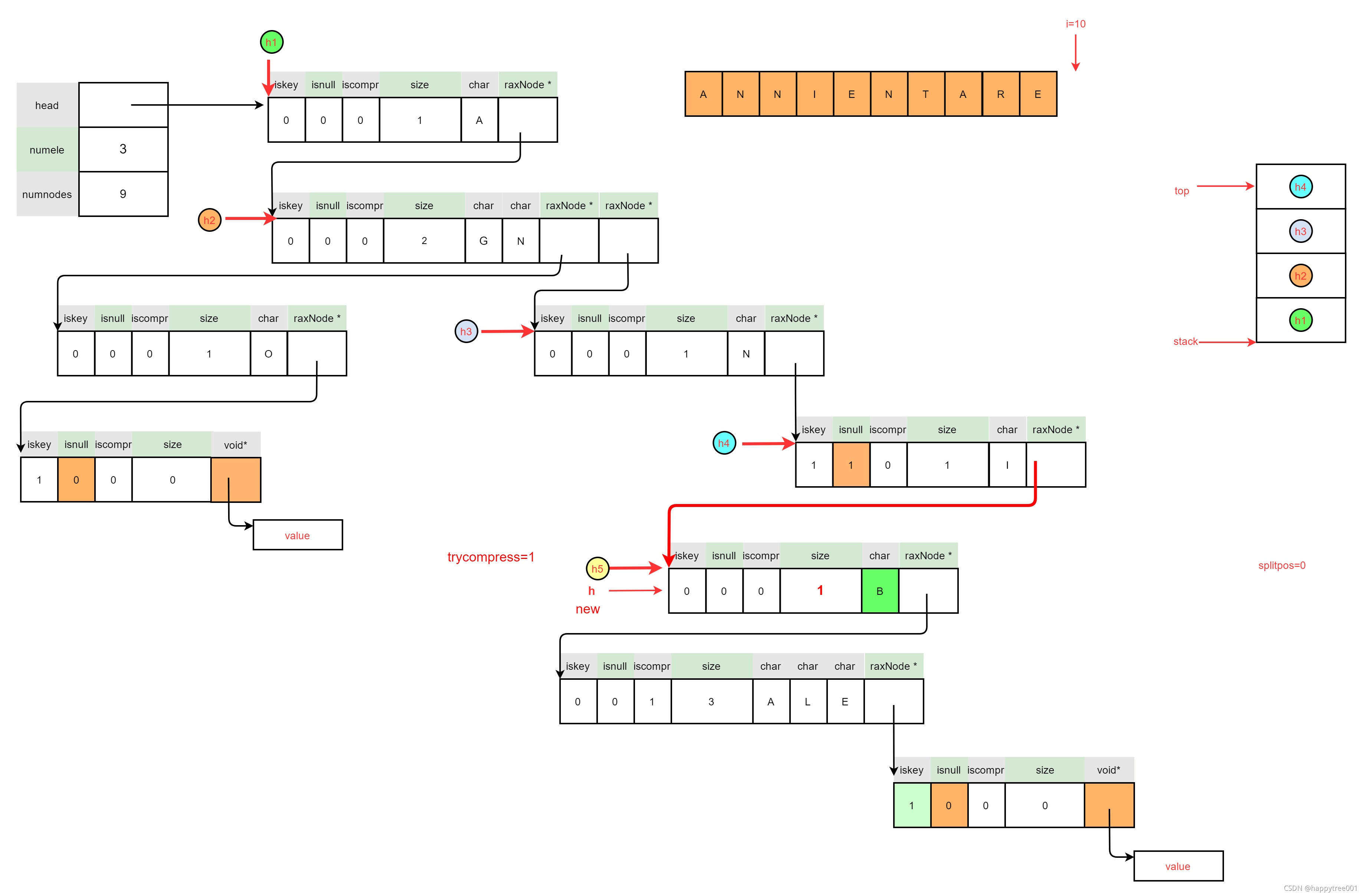
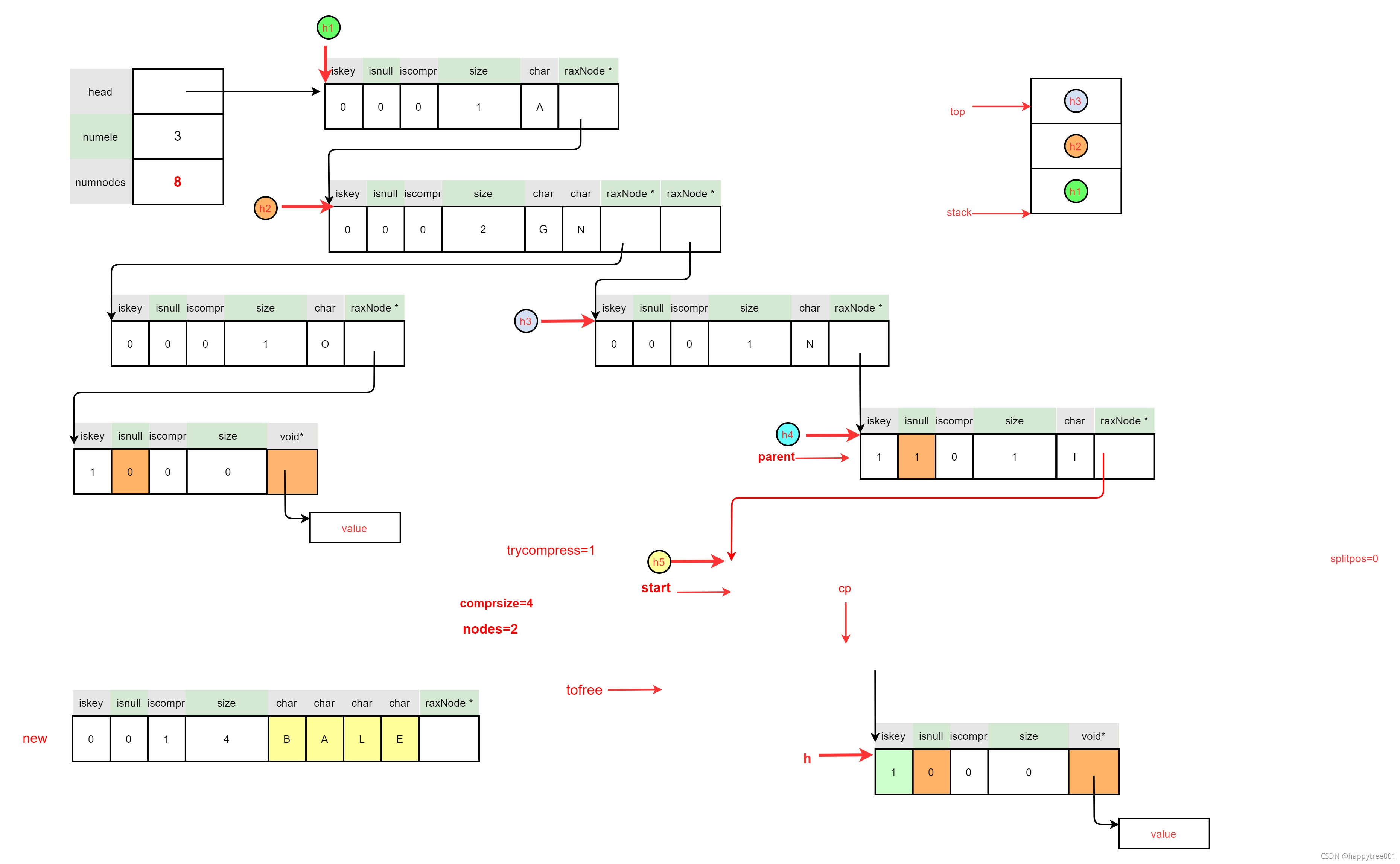
3.5.1.6 尝试压缩节点
3.5.1.6.1 查找可压缩的第一个节点
/* Try to reach the upper node that is compressible.
* At the end of the loop 'h' will point to the first node we
* can try to compress and 'parent' to its parent. */
raxNode *parent;
while(1) {
parent = raxStackPop(&ts);
if (!parent || parent->iskey ||
(!parent->iscompr && parent->size != 1)) break;
h = parent;
debugnode("Going up to",h);
}
raxNode *start = h; /* Compression starting node. */
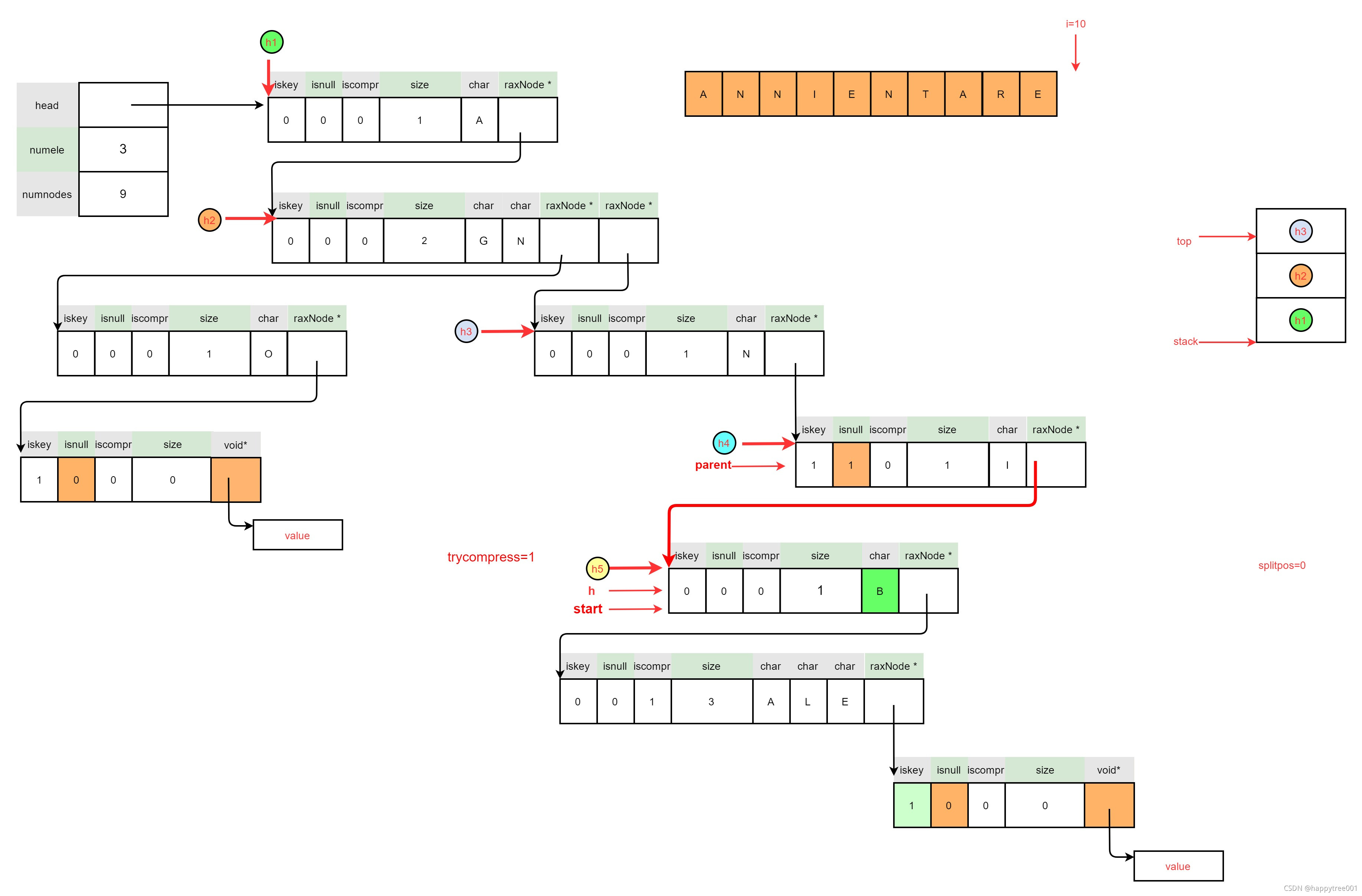
3.5.1.6.2 扫描整个可压缩链路
/* Scan chain of nodes we can compress. */
size_t comprsize = h->size;
int nodes = 1;
while(h->size != 0) {
raxNode **cp = raxNodeLastChildPtr(h);
memcpy(&h,cp,sizeof(h));
if (h->iskey || (!h->iscompr && h->size != 1)) break;
/* Stop here if going to the next node would result into
* a compressed node larger than h->size can hold. */
if (comprsize + h->size > RAX_NODE_MAX_SIZE) break;
nodes++;
comprsize += h->size;
}
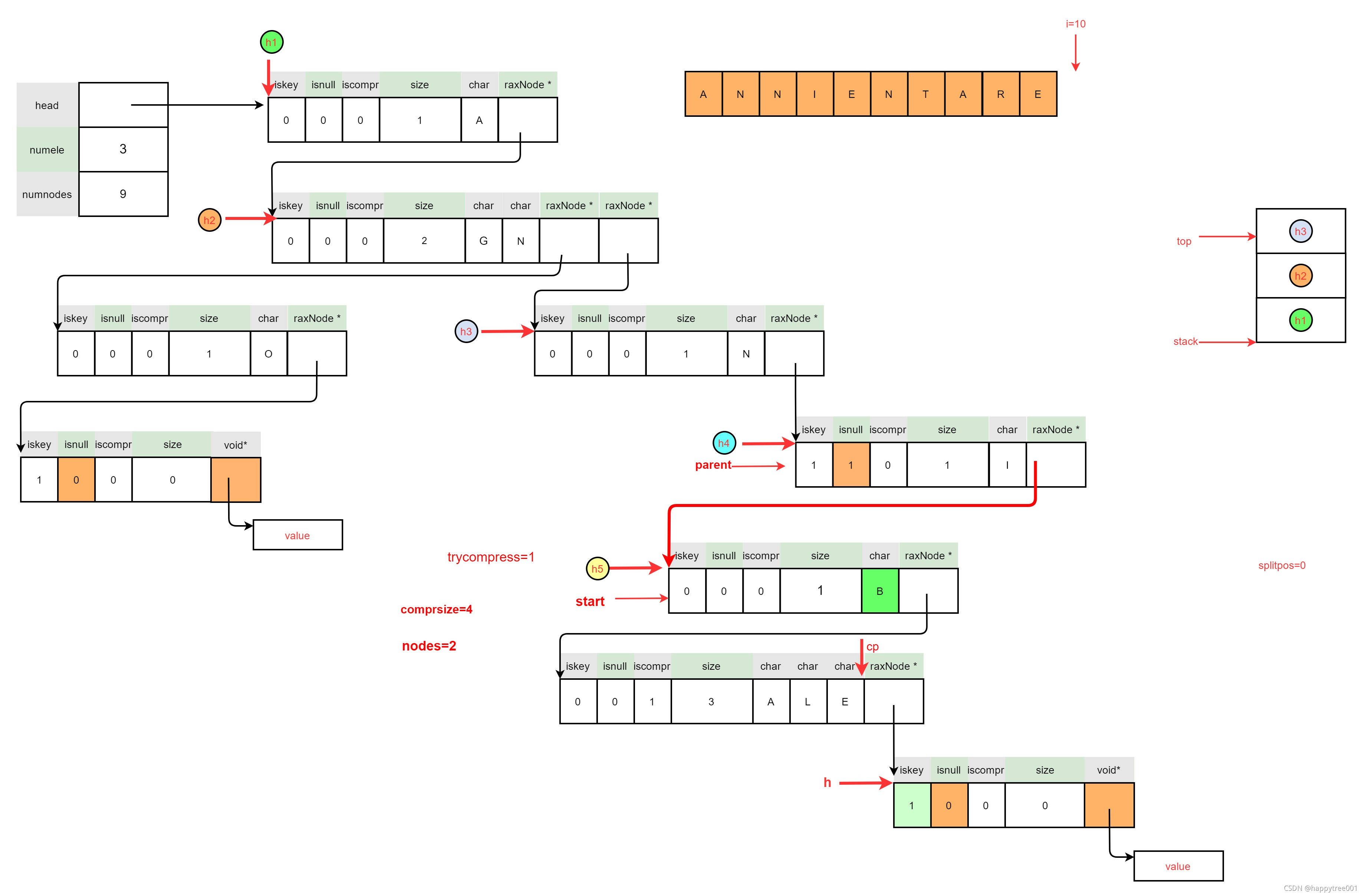
3.5.1.6.3 节点压缩
if (nodes > 1) 满足条件,所以可以进行节点压缩
- 创建新的压缩节点
/* Ifwe can compress, create the new node and populate it. */
size_t nodesize =
sizeof(raxNode)+comprsize+sizeof(raxNode*);
raxNode *new = rax_malloc(nodesize);
/* An out of memory here just means we cannot optimize this
* node, but the tree is left in a consistent state. */
if (new == NULL) {
raxStackFree(&ts);
return 1;
}
new->iskey = 0;
new->isnull = 0;
new->iscompr = 1;
new->size = comprsize;
rax->numnodes++;
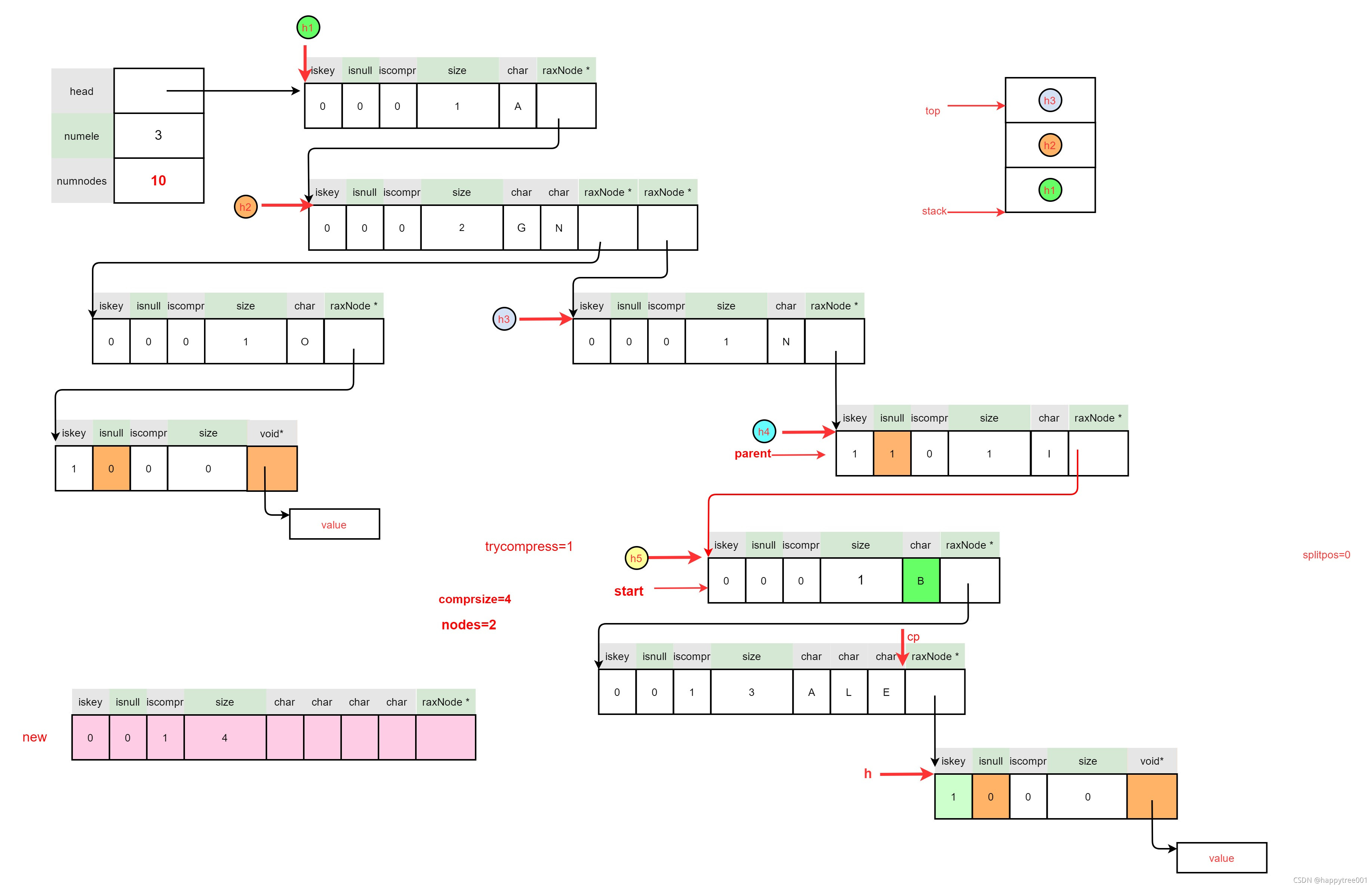
- 再次扫描,给新节点赋值,并且释放老节点
/* Scan again, this time to populate the new node content and
* to fix the new node child pointer. At the same time we free
* all the nodes that we'll no longer use. */
comprsize = 0;
h = start;
while(h->size != 0) {
memcpy(new->data+comprsize,h->data,h->size);
comprsize += h->size;
raxNode **cp = raxNodeLastChildPtr(h);
raxNode *tofree = h;
memcpy(&h,cp,sizeof(h));
rax_free(tofree); rax->numnodes--;
if (h->iskey || (!h->iscompr && h->size != 1)) break;
}
debugnode("New node",new);
- 重新连接节点连接
/* Now 'h' points to the first node that we still need to use,
* so our new node child pointer will point to it. */
raxNode **cp = raxNodeLastChildPtr(new);
memcpy(cp,&h,sizeof(h));
/* Fix parent link. */
if (parent) {
raxNode **parentlink = raxFindParentLink(parent,start);
memcpy(parentlink,&new,sizeof(new));
} else {
rax->head = new;
}
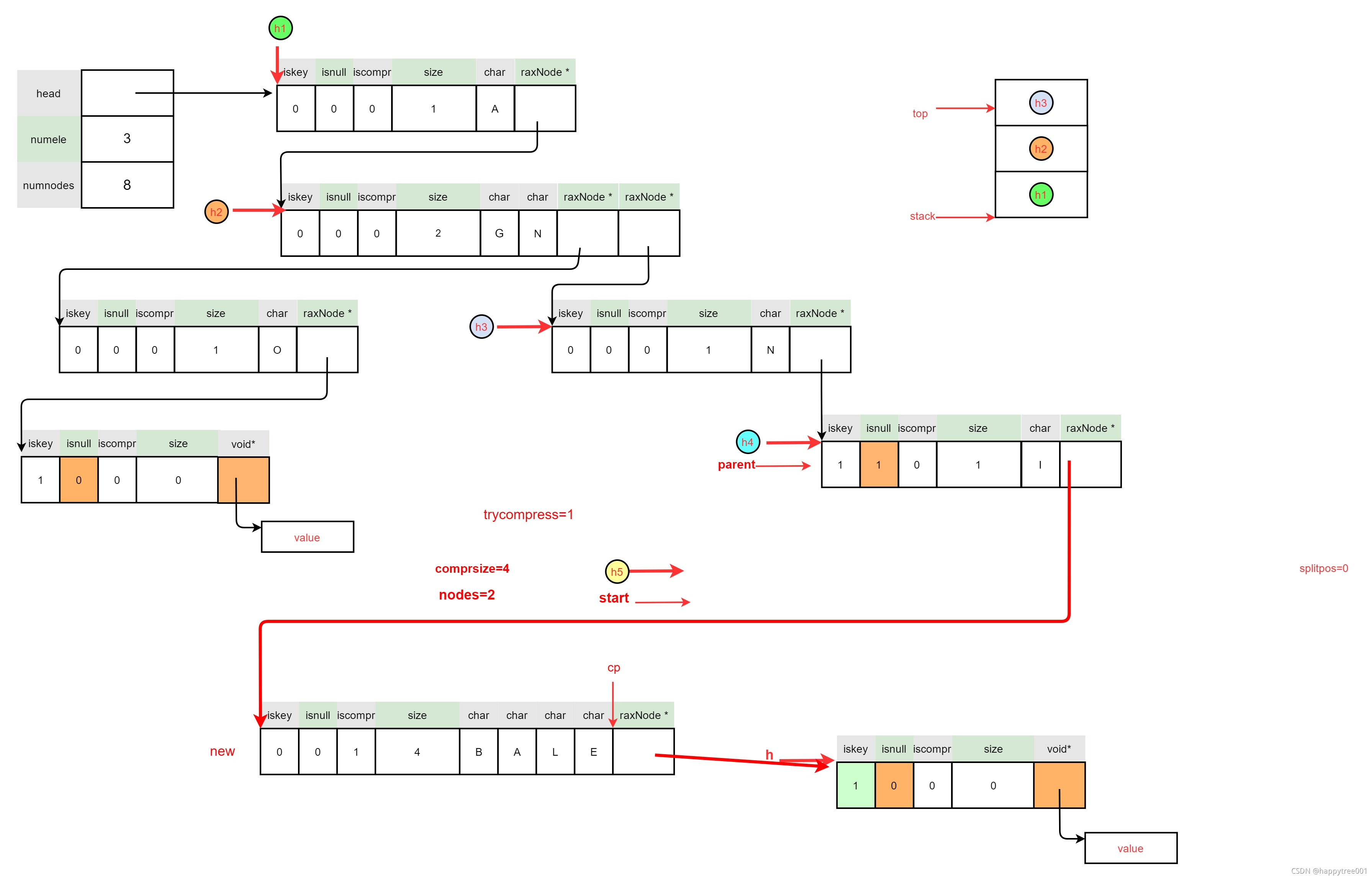
3.5.1.6 释放栈
raxStackFree(&ts);
/* Free the stack in case we used heap allocation. */
static inline void raxStackFree(raxStack *ts) {
if (ts->stack != ts->static_items) rax_free(ts->stack);
}