原文标题:Index Design of Electronic Medical Record Database Using Blockchain
原文作者:Jingwen Li,Jian Wang
原文地址:DOI 10.1109/ICMCCE51767.2020.00438
发表会议:2020 5th International Conference on Mechanical, Control and Computer Engineering (ICMCCE)
笔记整理:doxbwx@163,com
1.简介
电子简历(EMR)是一种高度敏感的医疗数据,存储在传统的SQL数据库中,很容易因为数据库的开放数据访问而导致数据被篡改。利用区块链的防篡改、可追溯、高共享等特点,与传统数据库方便查询用户数据的特点相结合,在保证医疗数据存储安全的情况下,方便用户查询检索。主要作出了以下几个方面的贡献:
- 作者设计了一个专门用于存储EMR的区块链系统
- 根据EMR的字段特征,设计了一个数据库表,用三种结构建立聚类索引和非聚类索引
- 基于数据库表的索引结构,用户可以在单字段或多字段组合中进行数据查询。
预备内容
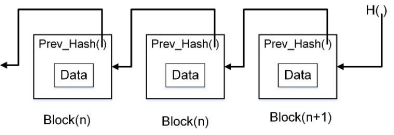
1.一般区块链结构如下图所示
? ? ? ? 区块链可以理解为一种分布式的数据库,它由多个区块按时间顺序链接在一起组成的p2p网络。

2.数据库中的索引
索引可以分为聚集索引和非聚集索引。
聚集索引可以通过主键值直接找到需要的数据,非聚集索引只能找到对应的主键值,然后再通过聚集索引中的主键找到最终的数据。两者之间的关系如下图所示。

常见的索引结构包括有B-树,B+树和bitmap index
B树:由下图所示,是一个M叉搜索树
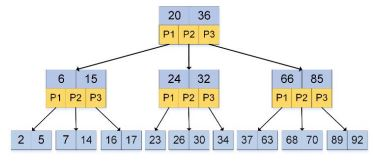
- num(根节点的子节点) = [2,M]
2. 除根节点外,num(非叶子节点的子树)=[M/2,M]
3. num(非叶子节点的关键字)=num(指向子节点的指针)-1
4. 非叶子节点的关键字K[1], K[2], … , K[M-1], 并且K[i] < K[i+1]
5. 非叶子节点P[1],P[2],… ,P[M]的指针,其中P[1]指向关键字小于K[1]的子树,P[M]指向关键字大于K[M-1]的子树,其他P[i]指向关键字属于(K[i-1],K[i])的子树
6. 所有叶子节点都在同一层
B+树:如下图所示,与B-树基本相同,差别在于

1.对于非叶节点,num(指向子节点的指针)=num(关键字)
2.非叶子节点作为索引,叶子节点存储关键词的数据记录
3.所有叶子节点形成一个有序的链表,这对范围查询很方便
位图索引:适用于一个字段只有几个固定的值
方案
作者把方案分为三个部分
- 用于存储医疗数据的区块链数据库
- 面向用户的数据库
- 建立索引和查询
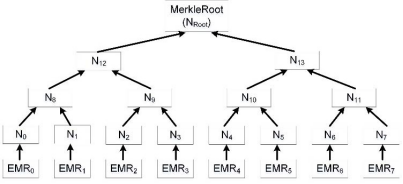
把数据存入EMR表中,并把它当作一个数据块,把数据块的哈希结果作为叶子节点的哈希值传入。
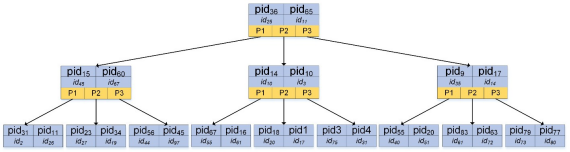
面向用户的数据库各字段定义为下图所示
建立索引
//在表patient_info(id)上创建聚类索引index_id
create unique index index_id on patient_info(id);
//在表patient_info(pid)上创建非聚类索引index_pid
create index index_id on patient_info(pid);
//在表patient_info(gender)上创建非聚类索引index_gender
create index index_gender on patient_info(gender);
//在表patient_info(dr)上创建非聚类索引index_dr
create index index_dr on patient_info(dr);
在主键上建立index_id索引,则B+树上叶子节点不仅存储节点的键值,还存储数据行信息。从数据行信息中可以找到EMR的物理地址,再从区块链数据库中下载EMR进行哈希处理,两者相比较,相等则没被篡改。

使用B树结构建立”index_pid“索引,因为每个病人都有id,所以每个节点都包含pid、id以及指针。检索到满足条件的pid后可以得到id,通过id再聚类索引叶子节点。
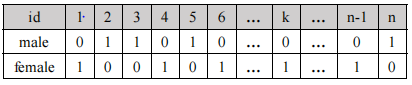
”gender“和"dr"字段重复率高,所以使用位图索引。当查询到性别为male时,male的向量为011010…等,再使用id满足该向量为1,继续在聚类索引树中查询,直到叶子节点满足条件为止。
检索算法
单字段查询语句
//在表patient_info(id)上创建聚类索引index_id
create unique index index_id on patient_info(id);
//在表patient_info(pid)上创建非聚类索引index_pid
create index index_id on patient_info(pid);
//在表patient_info(gender)上创建非聚类索引index_gender
create index index_gender on patient_info(gender);
多字段组合查询语句
//在表patient_info(dr)上创建非聚类索引index_dr
create index index_dr on patient_info(dr);
性能分析
用户输入一个查询条件时,主键将被非聚类索引找到。然后数据行也将通过聚集索引使用主键进行查询。这种情况下,索引的时间复杂性可以分为下面两种情况。
- Time1 = Time(Bitmap) + Time(B+Tree)
O1 = O(1) +O(log N) = O(log N) - Time2 = Time(B-Tree) + Time(B+Tree)
O2 = O(log N) + O(log N) = O(log N)
当用户输入多个条件查询,主键被几个非聚集索引找到,然后通过聚集索引进行查询。
- Time3 = Time(B-Tree) + Time(B+Tree) + Time(Bitmap)
O3 = mO(log N) + O(log N) + nO(1) = O(log N)
所以,平均时间复杂度为O(log N)
结论
作者建了一个专门用于存储EMR的区块链数据库,然后使用B-tree、B+tree和bitmap索引来建立数据库表的聚类索引和非聚类索引。可以满足用户不同的查询需求,可以准确地、快速地检索到EMR。作者将区块链数据库与传统SQL数据库结合,既满足了用户查询需求,又保证了EMR的安全性。但是该方案还有待改进,多字段的条件租合查询,还需要使用多个查询语句或嵌套语句来实现,时间成本还有待减少并且区块链数据库中用于存储EMR的Merkle树应该还可以改进,并且作者提出的该方案还没有经过实验论证。


