原文链接:http://tecdat.cn/?p=24861?
原文出处:拓端数据部落公众号
概括
- r 语言允许用户计算 lme 4 包中广义线性混合模型的功效。功率计算基于蒙特卡罗模拟。
- 它包括用于 (i) 对给定模型和设计进行功效分析的工具;(ii) 计算功效曲线以评估功效和样本量之间的权衡。
- 本文提供了一个教程,使用具有混合效果的计数数据的简单示例(具有代表环境监测数据的结构)。
介绍
假设检验的功效定义为假设原假设为假,检验拒绝原假设的概率。换句话说,如果一个效应是真实的,那么分析判断该效应具有统计显着性的概率是多少?
如果一项研究的功效不足,资源可能被浪费,真正的效果可能被遗漏。另一方面,一项大型研究的花费可能过大,因此其费用也会超过必要的范围。因此,在收集数据之前进行功效分析是一个很好的做法,以确保样本具有适当的规模来回答正在考虑的任何研究问题。
广义线性混合模型 (GLMM) 在生态学中很重要,它允许分析计数和比例以及连续数据,并控制空间非独立性.
蒙特卡罗模拟是一种灵活且准确的方法,适用于现实的生态研究设计。在某些情况下,我们可以使用解析公式来计算功效,但这些通常是近似值或需要特殊形式的设计?。仿真是一种适用于各种模型和方法的单一方法。即使公式可用于特定模型和设计,定位和应用适当的公式也可能非常困难,因此首选仿真。
对于对 r 不够熟悉的研究人员,设置模拟实验可能太复杂了。在本文中,我们介绍了一个工具来自动化这个过程。
r 包
有一系列的 r 包目前可用于混合模型的功效分析 。然而,没有一个可以同时处理非正态因变量和广泛的固定和随机效应规范。
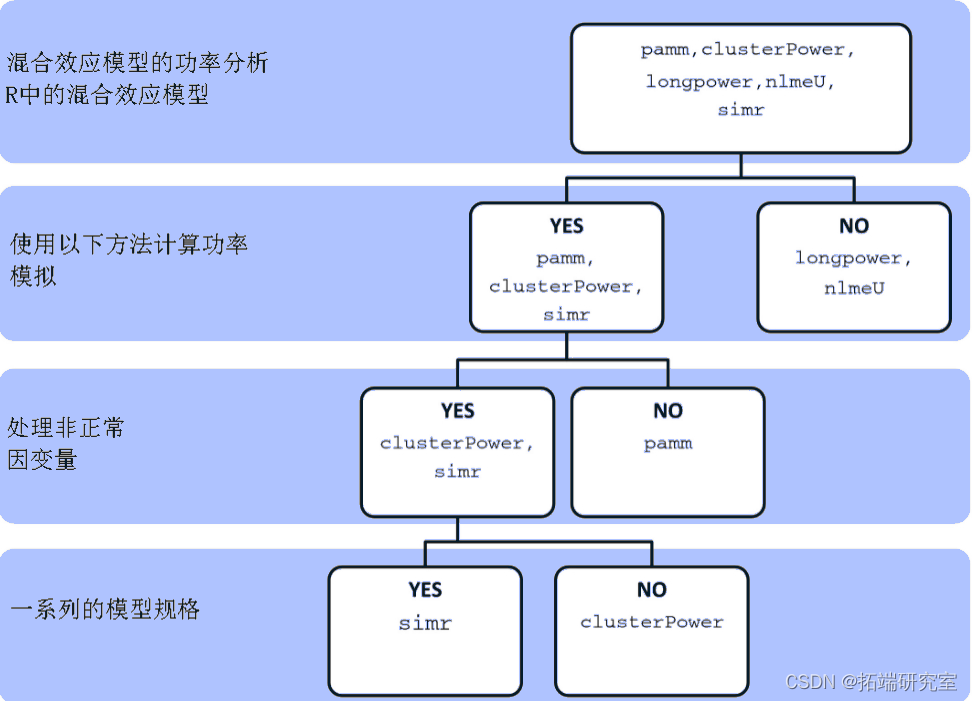
图1
r 旨在与任何可以与 lme 4 中的 lmer 或 glmer 配合的线性混合模型 (LMM) 或 GLMM 一起使用。这允许具有不同固定和随机效应规范的各种模型。还支持在 r 中使用 lm 和 glm 的线性模型和广义线性模型,以允许没有随机效应的模型。
r 中的功效分析从适合 lme 4 的模型开始。
在 r 中,通过重复以下三个步骤来计算功效:(i) 使用提供的模型模拟因变量的新值;(ii) 将模型重新拟合为模拟因变量;(iii) 对模拟拟合应用统计检验。在此设置中,已知存在测试效果,因此每个阳性测试都是真正的阳性,每个阴性测试都是 II 类错误。可以根据步骤 3 的成功和失败次数计算测试的功效。
教程
本教程使用包含的数据集。该数据集代表环境监测数据,在连续固定效应变量x?(例如研究年份)的10 个水平上测量三个组?g?(例如研究地点)的因变量?z?(例如鸟类丰度?)。还有一个连续因变量?y?,在本教程中没有使用。
拟合模型
我们首先将 lme 4 中的一个非常简单的泊松混合效应模型拟合到数据集。在这种情况下,我们有一个随机截距模型,其中每个组 ( g? ) 都有自己的截距,但这些组共享一个共同的趋势。
glm
summary

本教程重点介绍关于x?趋势的推断?。在这种情况下,x?的估计效应大小为?-0.11,使用默认z检验在 0.01 水平上显着?。
请注意,我们特意使用了一个非常简单的模型来使本文易于理解。例如,适当的分析会包含更多的组,并会考虑过度分散等问题。。
简单的功率分析
假设我们想重复这项研究。如果效果是真实的,我们是否有足够的功效来期待积极的结果?
指定效应量
在开始功效分析之前,重要的是要考虑您感兴趣的效果大小类型。功效通常随效果大小而增加,较大的效果更容易检测。回顾性“观察功效”计算,其中目标效应大小来自数据,给出误导性结果.
对于此示例,我们将考虑检测 -0.05 斜率的功效。可以使用 lme 4 函数拟合 glmer 模型中的固定效应。然后可以更改固定效应的大小。变量x?的固定效应的大小?可以从 -0.11 更改为 -0.05,如下所示:
fixe<‐ ‐0.05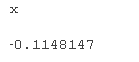
在本教程中,我们只更改变量x?的固定斜率?。但是,我们也可以更改随机效应参数或残差方差(适用于合适的模型)。
运行功效分析
一旦指定了模型和效应大小,在 r 中进行功效分析就非常容易了。由于这些计算基于蒙特卡罗模拟,因此您的结果可能略有不同。如果你想得到和教程一样的结果,你可以使用 set.seed(123)。
power

鉴于此特定设置,拒绝x?中零趋势的零假设的?能力约为 33%。这几乎总是被认为是不够的;传统上,80% 的功率被认为是足够的.
在实践中,? z检验可能不适合这样一个小例子。参数引导测试?可能是最终分析的首选。但是,更快的?z -test 更适合学习使用该包以及在功效分析期间进行初始探索性??工作。
增加样本量
在第一个示例中,估计功率很低。小型试点研究通常没有足够的功效来检测微小的影响,但更大的研究可能会。
试点研究对x 的?10 个值进行了观察,?例如代表研究第 1 年到第 10 年。在此步骤中,我们将计算将其增加到 20 年的影响。
modl2 <‐ extend
power(modl2)

沿参数指定要扩展的变量,n 指定要替换它的级别。扩展模型 2 现在将具有?从 1 到 20 的x?值,与以前一样分为三组,总共 60 行(与模型 1 中的 30 行相比)。
通过观察x 的?20 个值?,我们将有足够的能力来检测大小为 -0.05 的效应。
各种样本量的功效分析
当数据收集成本高昂时,用户可能只想收集达到一定统计能力所需的数据量。 功效曲线 函数可用于探索样本大小和功效之间的权衡。
确定所需的最小样本量
在前面的示例中,当对变量x 的20 个值进行观察时,我们发现了非常高的?功效?。我们能否减少这个数字,同时保持我们的功效高于通常的 80% 阈值?
poerCure
print
plot
请注意,我们已将此结果保存到变量 pc2 以匹配模型 2 中的编号。由于模型 1 没有足够的功率,我们没有通过 powerCurve 运行它。绘制的输出如图所示。?我们可以看到,检测x?趋势的?能力随着采样大小的增加而增加。这里的结果基于将模型拟合到 10 个不同的自动选择的子集。最小的子集仅使用前 3 年(即 9 个观测值),最大的子集使用所有 20 个假设研究年份(即 60 行数据)。该分析表明,该研究必须运行 16 年才能有≥80% 的功效来检测指定大小的影响。

图2
检测大小为 -0.05 的固定效应的功效 (±95% CI),使用 powerCurve 函数在一系列样本大小上计算。变量x?的不同值的数量?从 3 ( n? ?= 9) 到 20 ( n? ?= 60) 不等。
改变组的数量和大小
增加观察到的x?值的数量可能不可行?。例如,如果?x?是研究年份,我们可能不愿意等待更长时间的结果。在这种情况下,增加研究地点的数量或每个地点的测量数量可能是更好的选择。这两项分析从我们的原始模型 1 开始,该模型已有 10 年的研究时间。
添加更多组
我们可以像为x?添加额外值一样?为g?添加额外级别?。例如,如果变量?g?代表我们的研究站点,我们可以将站点数量从 3 增加到 15。
extend(n=15)
plot(pc3)与上一个示例的主要变化是我们将变量g?传递?给了沿参数。该分析的输出如图 1 所示。要达到 80% 的功率,我们至少需要 11 个站点。
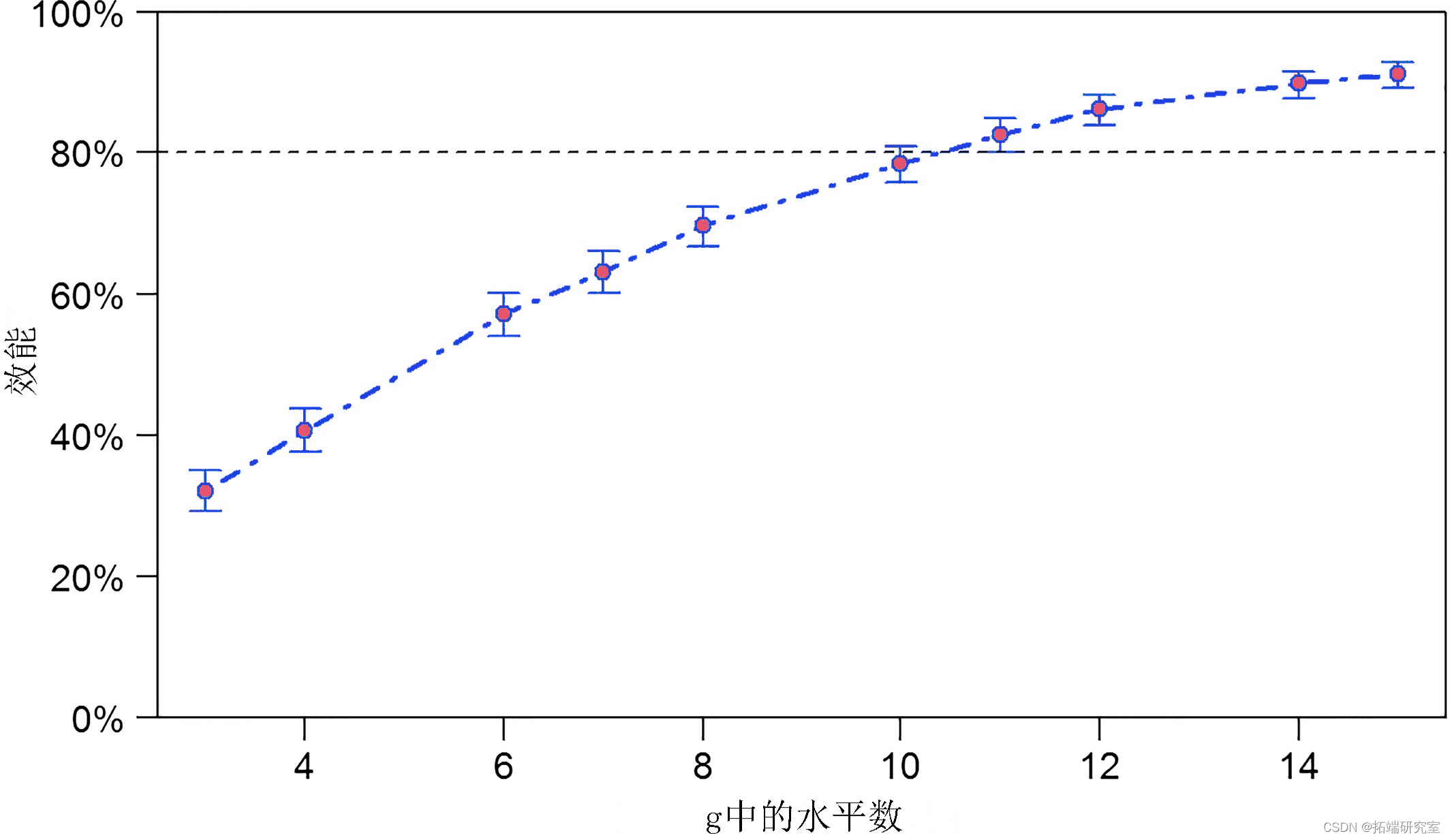
图 3
检测大小为 -0.05 的固定效应的功效 (±95% CI),使用 powerCurve 在一系列样本大小上计算。因子g?的级别数?从 3 ( n? ?= 30) 到 15 ( n? ?= 150) 不等。
增加组内的大小
我们可以用内参数替换扩展和 powerCurve 的沿参数以增加组内的样本大小。每个组在x?和?g 的?每个水平上只有一个观察值?。我们可以将其扩展到每个站点每年 5 次观测,??如下所示:
extend( n=5)
plot(p4)
请注意 powerCurve 的breaks 参数。为x?和?g 的?每个组合提供一到五个观察结果?。图表明每年每个站点 4 次观测会给我们 80% 的效力。
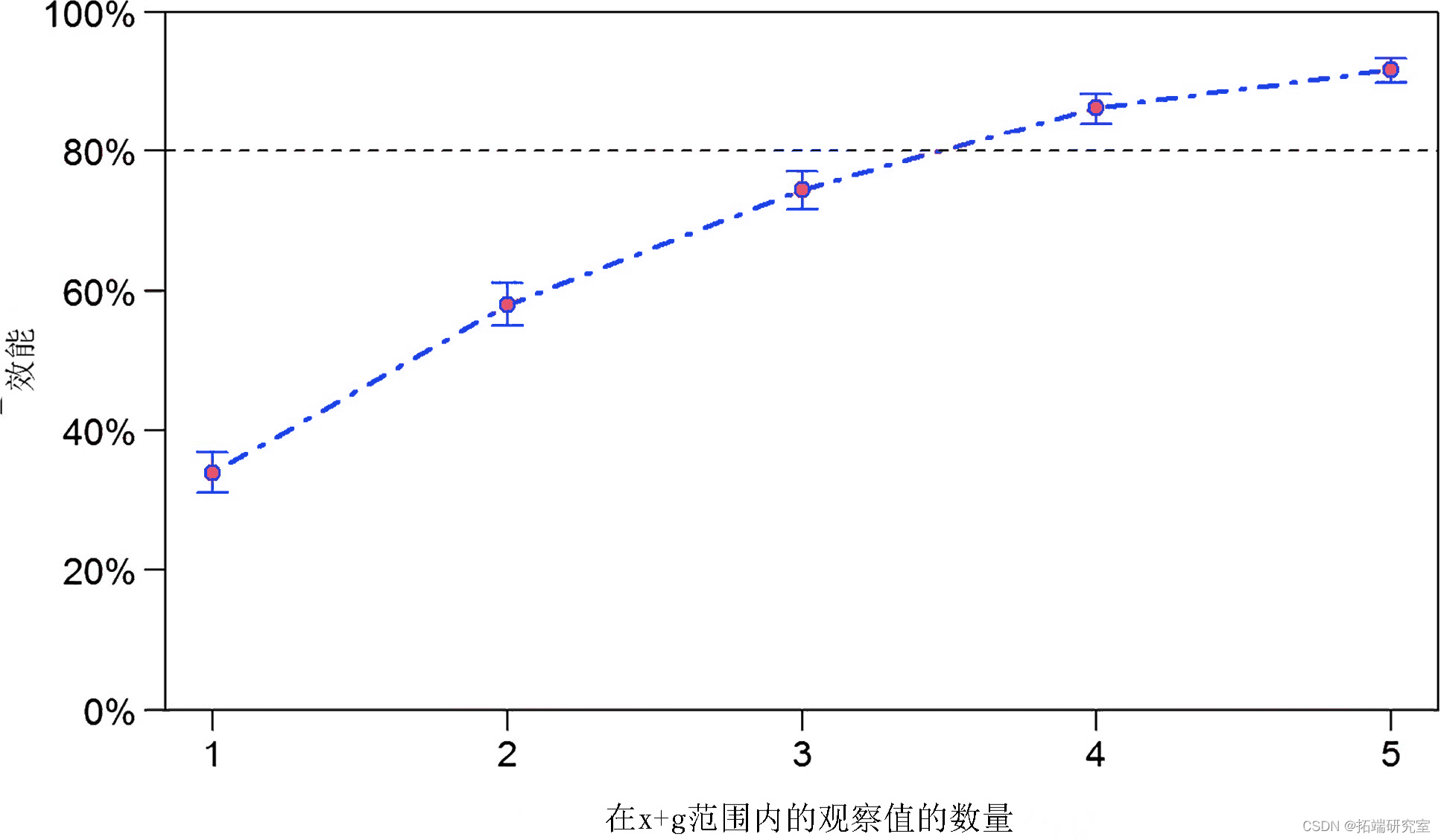
图 4
检测大小为 -0.05 的固定效应的功效 (±95% CI),使用 powerCurve 函数在一系列样本大小上计算。x?和?g 的?每个组合的观察数?从 1 ( n? ?= 30) 到 5 ( n? ?= 150) 不等。

最受欢迎的见解
1.Matlab马尔可夫链蒙特卡罗法(MCMC)估计随机波动率(SV,Stochastic Volatility) 模型
3.WinBUGS对多元随机波动率模型:贝叶斯估计与模型比较
4.R语言回归中的hosmer-lemeshow拟合优度检验