目录
🍎走进关联规则
🍊什么是关联规则?
🐾🐾情景引入:🍺啤酒与尿布🍼
在一家超市里,有一个有趣的现象:尿布和啤酒赫然摆在一起出售。但是这个奇怪的举措却使尿布和啤酒的销量双双增加了。这不是一个笑话,而是发生在美国沃尔玛连锁店超市的真实案例,并一直为商家所津津乐道。沃尔玛拥有世界上最大的数据仓库系统,为了能够准确了解顾客在其门店的购买习惯,沃尔玛对其顾客的购物行为进行购物篮分析,想知道顾客经常一起购买的商品有哪些。沃尔玛数据仓库里集中了其各门店的详细原始交易数据。在这些原始交易数据的基础上,沃尔玛利用数据挖掘方法对这些数据进行分析和挖掘。一个意外的发现是:"跟尿布一起购买最多的商品竟是啤酒!
经过大量实际调查和分析,揭示了一个隐藏在"尿布与啤酒"背后的美国人的一种行为模式:在美国,一些年轻的父亲下班后经常要到超市去买婴儿尿布,而他们中有30%~40%的人同时也为自己买一些啤酒。产生这一现象的原因是:美国的太太们常叮嘱她们的丈夫下班后为小孩买尿布,而丈夫们在买尿布后又随手带回了他们喜欢的啤酒。
这就是隐藏在实际生活中的关联规则吗,也是数据挖掘的一种形式,生活中的各类事物都会产生价值,善于挖掘事物的价值就会有不一样的价值。
联规则最初提出的动机是针对购物篮分析(Market Basket Analysis)问题提出的。假设分店经理想更多的了解顾客的购物习惯。特别是,想知道哪些商品顾客可能会在一次购物时同时购买?
为回答该问题,可以对商店的顾客事物零售数量进行购物篮分析。该过程通过发现顾客放入“购物篮”中的不同商品之间的关联,分析顾客的购物习惯。这种关联的发现可以帮助零售商了解哪些商品频繁的被顾客同时购买,从而帮助他们开发更好的营销策略。
关联规则是指事物间的相互联系,反映了一个事物与其他事物之间的相互依存性和关联性。如果两个或者多个事物之间存在一定的关联关系,那么其中一个事物就能够通过其他事物预测得到。
🍒关联规则的分类
按处理值分类,关联规则可以分为量化型和布尔型
布尔型关联规则是研究数据项在某个事务中是否会出现。量化型关联规则主要是离散型的数据,关联规则中的数据项是数量型的。
在对量化进行关联规则进行挖掘时,通常使用统计学、离散方法等对量化数值进行离散化。分化成几个离散区间,从而转换成布尔型关联规则挖掘。
关联规则按所涉及的抽象层次可以分为单层和多层
比如每科成绩之间的关联挖掘就是单层的。而专业课、公共课等之间的关联挖掘,就是多层的。因为 他们是属于不同层级。
根据数据维数则可以分为,单维和多维
比如,购买网球,只涉及到一个维度。年龄购买网球,则涉及到年龄和网球两个维度。
🍉关联规则的基本概念
(1)项
对一个数据表而言,表的每个字段都具有一个或多个不同的值。字段的每种取值都是一个项Item。
(2)项集
项的集合称为项集itemset。包含k个项的项集被称为k-项集,k表示项集中项的数目。由所有的项所构成的集合是最大的项集,一般用符号I表示。
(3)事务
事务是项的集合。本质上,一个事务就是事实表中的一条记录。事务是项集I的子集。事务的集合称为事务集。一般用符号D表示事务集/事务数据库。
(4)关联规则
给定一个事务集D,挖掘关联规则的问题就变成如何产生支持度和可信度分别大于用户给定的最小支持度和最小可信度的关联规则的问题。(标准)
(5)支持度(同时,交;元组总数)
若D中的事务包含A∪B的百分比为s,则称关联规则AB的支持度为s。即:support(AB )= P(A∪B ) = 包含A和B的元组数/元组总数
(6)可信度(同时,交;条件概率)
若D中包含A的事务同时也包含B的的百分比为c,则称关联规则 AB 的置信度/可信度为c,即:confidence(AB )=P(B|A) = 包含A和包含B的元组数/包含A的元组数 = support(A∪B )/support(A)
根据上面的例子,可以求解到苹果——>啤酒的置信度=3/8 /4/8=3/4
75%的置信度
(7)频繁项集
项集的出现频率是包含项集的事务数,简称项集的频率;项集满足最小支持度阈值minsup,如果项集的出现频率大于或等于minsup与D中事务总数的乘积;满足最小支持阈值的项集就称为频繁项集(大项集)。频繁k项集的集合记为Lk;
如何得出频繁项集,apriori算法的价值所在
(8)强关联规则
大于或等于最小支持度阈值和最小置信度阈值的规则叫做强关联规则
关联分析的最终目的,就是为了找出强关联规则??????????
算法
那么,关联规则的本质,其实就是挖掘频繁项,那么算法的目的也就是尽可能快速有效的挖掘不同事物间 关系出现的频率。
而衡量规则是否成立的两个参考维度,就是支持度和置信度。
常用的算法有 Apriori 算法?,FP-growth 算法。这两个算法,前者主要用迭代方法挖掘,不适用于多维挖掘。后者利用存储优化,大幅提高了挖掘性能。
(9)Lift(提升度)
指A项和B项一同出现的频率,但同时要考虑这两项各自出现的频率。公式表达:{A→B}的提升度={A→B}的置信度/P(B):
提升度反映了关联规则中的A与B的相关性,提升度>1且越高表明正相关性越高,提升度<1且越低表明负相关性越高,提升度=1表明没有相关性。负值,商品之间具有相互排斥的作用。
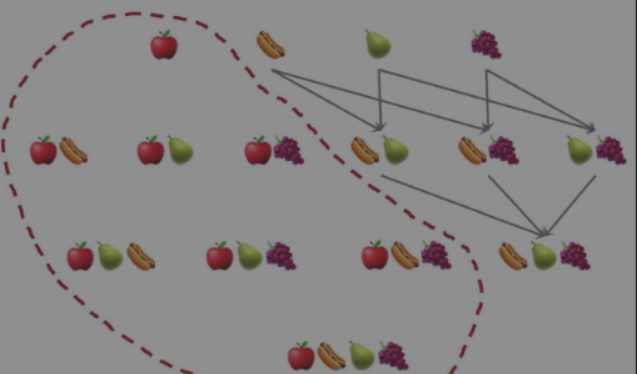
🎈🎈?通过了解上面的一些概念知识,这里给出来一个具体的实例:
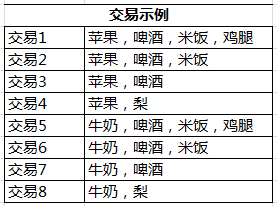
事务: 每一条交易称为一个事务,例如:上表中包含8个事务。
项:??? 交易中的每一个物品称为一个项,例如:苹果、啤酒。
项集:包含零个或者多个项的集合叫做项集,例如{苹果,啤酒} 、{牛奶,啤酒,米饭}。
?k-项集:包含k个项的项集叫做k-项集。例如{苹果}叫做1-项集,{牛奶,啤酒,米饭}叫做3-项集。
前件和后件:对于规则{苹果}->{啤酒},{苹果}叫前件,{啤酒}叫后件。
📢 📣🍩🍩下面也通过对三个度量指标进行实例的分析
1?? 支持度:
{苹果}在8次交易中出现了4次,所以其支持度为50%。
一个项集也可以包含多项,比如{苹果,啤酒,米饭}的支持度为2/8,即25%。
可以人为设定一个支持度阈值,当某个项集的支持度高于这个阈值时,我们就把它称为频繁项集。
2?? 置信度:
{苹果→啤酒}的置信度=(支持度{苹果,啤酒}/支持度{苹果})=3/4,即75%。
置信度有一个缺点,那就是它可能会错估某个关联规则的重要性。只考虑了苹果的购买频率,而并未考虑啤酒的购买频率。如果啤酒也很受欢迎(支持度很高),如上表,那么包含苹果的交易显然很有可能也包含啤酒,这会抬高置信度指标。
3?? 提升度:
{苹果→啤酒}的提升度等于{苹果→啤酒}的置信度除以{啤酒}的支持度,{苹果→啤酒}的提升度等于1,这表示苹果和啤酒无关联。
{X→Y}的提升度大于1,这表示如果顾客购买了商品X,那么可能也会购买商品Y;而提升度小于1则表示如果顾客购买了商品X,那么不太可能再购买商品Y。
为什么说置信度是有缺点的呢?下面我们看一个实际的例子@快来看📢 📣📢
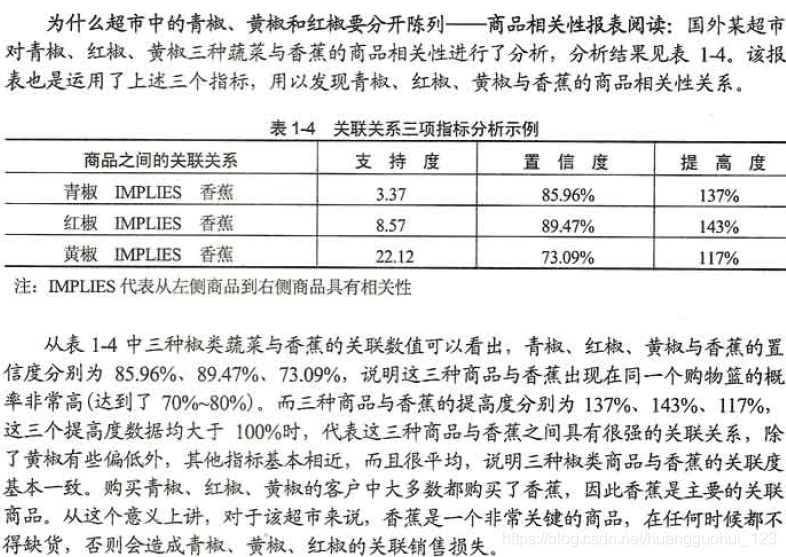
?置信度的局限——错估某个关联规则的重要性
📑实际案例
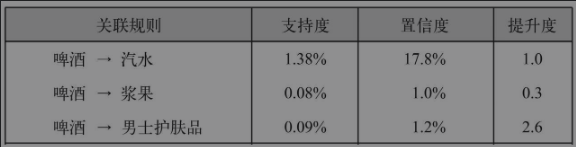
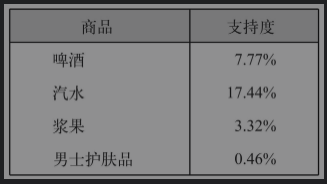
?各商品在与啤酒相关的关联规则中的支持度?
置信度很高,但是提升度较低,关联效果不好!
{啤酒→汽水}规则的置信度最高,为17.8%。然而,在所有交易中,二者出现的频率都很高,所以它们之间的关联可能只是巧合。这一点可以通过其提升度为1得到印证,即购买啤酒和购买汽水这两个行为之间并不存在关联。
置信度很低,但是关联效果较好!
比如{啤酒→男士护肤品}规则的置信度低,这是因为男士护肤品的总购买量不大。
尽管如此,如果一位顾客买了男士护肤品,那么很有可能也会买啤酒,这一点可以从较高的提升度(2.6)推断出来。
提升度为负数,无关联!
{啤酒→浆果}的情况则恰好相反。从提升度小于1这一点,我们可以得出结论:如果一位顾客购买了啤酒,那么可能不会买浆果。
虽然很容易算出各个商品组合的销售频率,但是商家往往更感兴趣的是所有的热销商品组合。为此,需要先为每种可能的商品组合计算支持度,然后找到支持度高于指定阈值的商品组合。
那么如何去计算和找出热销商品的组合策略呢?手动的去就是,综合比对吗?如果是在理解算法原理,那倒是可以,但是如果是在进行项目实战,显然无法进行。
提升度难道是最好的判断标准吗?显然不是,下面我们一起看看,提升度会受到哪些因素的影响吧!以及提升度的来源是什么?
提升度和零事务的关系
假设:10000个超市订单(10000个事务),其中购买三元牛奶(A事务)的6000个,购买伊利牛奶(B事务)的7500个,4000个同时包含两者。
三元牛奶(A事务)和伊利牛奶(B事务)的支持度为:0.4
三元牛奶(A事务)对伊利牛奶(B事务)的置信度为:0.67
说明在购买三元牛奶后,有0.67的用户去购买伊利牛奶。
伊利牛奶(B事务)对三元牛奶(A事务)的置信度为:0.53
说明在购买伊利牛奶后,有0.53的用户去购买三元牛奶。
在没有任何条件下,B事务的出现的比例是0.75,而出现A事务,且同时出现B事务的比例是0.67,也就是说设置了A事务出现这个条件,B事务出现的比例反而降低了。这说明A事务和B事务是排斥的。
我们把0.67/0.75的比值作为提升度,即P(B|A)/P(B),称之为A条件对B事务的提升度,即有A作为前提,对B出现的概率有什么样的影响,如果提升度=1说明A和B没有任何关联,如果<1,说明A事务和B事务是排斥的,>1,我们认为A和B是有关联的,但是在具体的应用之中,我们认为提升度>3才算作值得认可的关联。
提升度是一种很简单的判断关联关系的手段,但是在实际应用过程中受零事务的影响比较大,零事务在上面例子中可以理解为既没有购买三元牛奶也没有购买伊利牛奶的订单。
数值为10000-4000-2000-3500=500,可见在本例中,零事务非常小,但是在现实情况中,零事务是很大的。在本例中如果保持其他数据不变,把10000个事务改成1000000个事务,那么计算出的提升度就会明显增大,此时的零事务很大(1000000-4000-2000-3500),可见提升度是与零事务有关的,零事务越多,提升度越高。
先验原则
简单地说,先验原则是指,如果某个项集出现得不频繁,那么包含它的任何更大的项集必定也出现得不频繁。这就是说,如果{啤酒}是非频繁项集,那么{啤酒,比萨}也必定是非频繁项集。因此,在整理频繁项集列表时,既不需要考虑{啤酒,比萨},也不需要考虑其他任何包含啤酒的项集。
随后就会引入最小支持度和最小置信度的概念
步骤1:列出只包含一个元素的项集,比如{苹果}和{梨}。
步骤2:计算每个项集的支持度,保留那些满足最小支持度阈值条件的项集,淘汰不满足的项集。
步骤3:向候选项集(淘汰步骤2不满足的项集后的结果)中增加一个元素,并利用在步骤2中保留下来的项集产生所有可能的组合。
步骤4:重复步骤2和步骤3,为越来越大的项集确定支持度,直到没有待检查的新项集。
?
举个例子,假设我们的任务是找到具有高置信度的关联规则。如果{啤酒,薯片→苹果}规则的置信度很低,那么所有包含相同元素并且箭头右侧有苹果的规则都有很低的置信度,包括{啤酒→苹果,薯片}和{薯片→苹果,啤酒}。如前所述,根据先验原则,这些置信度较低的规则会被移除。这样一来,待检查的候选规则就更少了。
这样对计算的复杂度和效率就会有很大的提升空间
实际案例
🍝下面给出一个具体的关联规则的案例🍝
?代码实战
频繁项集和支持度
from numpy import *
# 构造数据
def loadDataSet():
return [[1, 3, 4], [2, 3, 5], [1, 2, 3, 5], [2, 5]]
# 将所有元素转换为frozenset型字典,存放到列表中
def createC1(dataSet):
C1 = []
for transaction in dataSet:
for item in transaction:
if not [item] in C1:
C1.append([item])
C1.sort()
# 使用frozenset是为了后面可以将这些值作为字典的键
return list(map(frozenset, C1)) # frozenset一种不可变的集合,set可变集合
# 过滤掉不符合支持度的集合
# 返回 频繁项集列表retList 所有元素的支持度字典
def scanD(D, Ck, minSupport):
ssCnt = {}
for tid in D:
for can in Ck:
if can.issubset(tid): # 判断can是否是tid的《子集》 (这里使用子集的方式来判断两者的关系)
if can not in ssCnt: # 统计该值在整个记录中满足子集的次数(以字典的形式记录,frozenset为键)
ssCnt[can] = 1
else:
ssCnt[can] += 1
numItems = float(len(D))
retList = [] # 重新记录满足条件的数据值(即支持度大于阈值的数据)
supportData = {} # 每个数据值的支持度
for key in ssCnt:
support = ssCnt[key] / numItems
if support >= minSupport:
retList.insert(0, key)
supportData[key] = support
return retList, supportData # 排除不符合支持度元素后的元素 每个元素支持度
# 生成所有可以组合的集合
# 频繁项集列表Lk 项集元素个数k [frozenset({2, 3}), frozenset({3, 5})] -> [frozenset({2, 3, 5})]
def aprioriGen(Lk, k):
retList = []
lenLk = len(Lk)
for i in range(lenLk): # 两层循环比较Lk中的每个元素与其它元素
for j in range(i+1, lenLk):
L1 = list(Lk[i])[:k-2] # 将集合转为list后取值
L2 = list(Lk[j])[:k-2]
L1.sort(); L2.sort() # 这里说明一下:该函数每次比较两个list的前k-2个元素,如果相同则求并集得到k个元素的集合
if L1==L2:
retList.append(Lk[i] | Lk[j]) # 求并集
return retList # 返回频繁项集列表Ck
# 封装所有步骤的函数
# 返回 所有满足大于阈值的组合 集合支持度列表
def apriori(dataSet, minSupport = 0.5):
D = list(map(set, dataSet)) # 转换列表记录为字典 [{1, 3, 4}, {2, 3, 5}, {1, 2, 3, 5}, {2, 5}]
C1 = createC1(dataSet) # 将每个元素转会为frozenset字典 [frozenset({1}), frozenset({2}), frozenset({3}), frozenset({4}), frozenset({5})]
L1, supportData = scanD(D, C1, minSupport) # 过滤数据
L = [L1]
k = 2
while (len(L[k-2]) > 0): # 若仍有满足支持度的集合则继续做关联分析
Ck = aprioriGen(L[k-2], k) # Ck候选频繁项集
Lk, supK = scanD(D, Ck, minSupport) # Lk频繁项集
supportData.update(supK) # 更新字典(把新出现的集合:支持度加入到supportData中)
L.append(Lk)
k += 1 # 每次新组合的元素都只增加了一个,所以k也+1(k表示元素个数)
return L, supportData
dataSet = loadDataSet()
L,suppData = apriori(dataSet)
print(L)
print(suppData)也可以直接调用包:
from efficient_apriori import apriori
# 挖掘频繁项集和频繁规则
itemsets, rules = apriori(transactions, min_support=0.5, min_confidence=1)
print("频繁项集:", itemsets)
print("关联规则:", rules)置信度调用
#!/usr/bin/python
# -*- coding:utf-8 -*-
from itertools import combinations
#读取数据
def readdata(filename):
data = []
with open(filename, 'r') as f:
while True:
line = f.readline()
if not line:
break
data.append([int(_) for _ in line.split()])
return data
def subtract_item_set(pre_discard_itemset, candidate_set):
'''
首先去除候选集中不符合非频繁项集的那些元素,
在当前候选集中去掉上一轮删除的项集,
比如{2, 3}是非频繁项集,那么就将删除candidate_set中的{2, 3, x}这些项集
Parameters:
-----------
pre_discard_itemset: 上一轮删除的项集
candidate_set: 上一次产生的候选集
Returns:
--------
返回经过pre_discard_itemset筛选后的项集列表
'''
saved_item_set = set()
discard_item_set = set()
for item in candidate_set:
is_discard = False
for d_item in pre_discard_itemset:
if d_item.issubset(item):
is_discard = True
if is_discard:
discard_item_set.add(tuple(item))
else:
saved_item_set.add(tuple(item))
# saved_item_set, discard_item_set
return [set(i) for i in saved_item_set], [set(i) for i in discard_item_set]
def scan_data_set(data_set, candidate_set, min_support):
'''
扫描一遍数据集,从候选集中挑出满足支持度的频繁项集,
同时记录每个项集的支持度(供后面置信度计算)
'''
data_set = [set(i) for i in data_set]
data_set_size = len(data_set)
candidate_set_size = len(candidate_set)
cand_set_count = [0 for i in range(candidate_set_size)]
# 对候选集中的元素通过遍历数据集得到他们出现的次数
for i in range(candidate_set_size):
for ds in data_set:
if candidate_set[i].issubset(ds):
cand_set_count[i] += 1
saved_item_set = []
discard_item_set = []
support_data = []
# 删除不满足支持度的
for i in range(candidate_set_size):
support = cand_set_count[i] * 1.0 / data_set_size
if support >= min_support:
saved_item_set.append(candidate_set[i])
support_data.append(support)
else:
discard_item_set.append(candidate_set[i])
return saved_item_set, discard_item_set, support_data
def gen_cand_set(data_set, previous_freq_set, k):
'''
从上一次生成的候选集中产生本次的候选集(未经过支持度筛选处理的),
只是单纯生成下一轮的组合集
Parameters:
-----------
data_set: 数据集,用以生成k为1的项集
previous_freq_set: 上一次产生的候选集
k: 本次产生的候选集中项目的大小
Returns:
--------
返回列表存储的项集,每个项集是一个集合set, [{0}, {1}, {2}, {3}, {4}...]
'''
if k == 1:
# 列表解析
item_set = set([item for sublist in data_set for item in sublist]) # 或者item_set = set(sum(data_set, []))
return [set([i]) for i in item_set]
elif k > 1:
cur_freq_set = set()
pre_fre_set_len = len(previous_freq_set)
for i in range(pre_fre_set_len):
for j in range(i + 1, pre_fre_set_len):
# 遍历所有的两两组合,并将其加入到集合中
# {(1, 2, 3), (1, 3, 5), (2, 3, 4)}
s = previous_freq_set[i] | previous_freq_set[j]
if len(s) == k:
cur_freq_set.add(tuple(s))
return [set(i) for i in cur_freq_set]
def gen_frequecy_set(data_set, min_support):
'''
生成频繁项集
Returns:
--------
freq_item_set: [[set(item1), set(item2)..]...] 存储频繁项集
item_set_support: [[support_score1, s_score2..]] 每个项集对应的支持度分值
'''
freq_item_set = []
item_set_support = []
discard_item_set = None
cur_dis_item_set_1, cur_dis_item_set_2 = [], []
cur_item_set_size = 0
while True:
# 循环产生项集大小为1, 2...的项集
cur_item_set_size += 1
if cur_item_set_size == 1:
# 产生初始的候选集
cur_candiate_set = gen_cand_set(data_set, [], cur_item_set_size)
# 将候选集分成要满足支持度的集合和不满足支持度的集合,同时记录满足支持度集合对应的支持度分值
saved_item_set, cur_dis_item_set_1, support_data = scan_data_set(data_set, cur_candiate_set, min_support)
else:
# 生成该轮候选集
cur_candiate_set = gen_cand_set(data_set, freq_item_set[-1], cur_item_set_size)
# 去除候选集中不符合非频繁项集的那些元素
cur_candiate_set, cur_dis_item_set_1 = subtract_item_set(discard_item_set, cur_candiate_set)
# 对剩下的候选集,进行遍历数据集,得到保存、丢弃、支持度集合
saved_item_set, cur_dis_item_set_2, support_data = scan_data_set(data_set, cur_candiate_set, min_support)
if saved_item_set == []: # 如果该轮没有产生任何频繁项集,则下一轮也不会产生新的频繁项集了,退出
break
freq_item_set.append(saved_item_set) # freq_item_set存储每一轮产生的频繁项集
discard_item_set = cur_dis_item_set_1 # discard_item_set存储每一轮产生的要丢弃的项集
discard_item_set.extend(cur_dis_item_set_2)
item_set_support.append(support_data) # item_set_support存储每一轮产生的频繁项集对应的支持度值
return freq_item_set, item_set_support
def gen_association_rules(freq_item_set, support_data, min_confd):
'''
生成关联规则
Returns:
--------
association_rules: [(set(item1, item2, ...), itemx, confidence_score), ..]
存储关联规则,list存储,每个元素都是一个3元组,分别表示item1 和 item2.. 推出 itemx,置信度为confidence_score
'''
association_rules = []
for i in range(1, len(freq_item_set)):
for freq_item in freq_item_set[i]: # 对频繁项集的每一项尝试生成关联规则
gen_rules(freq_item, support_data, min_confd, association_rules)
return association_rules
def gen_rules(freq_item, support_data, min_confd, association_rules):
'''
生成关联规则,然后存储到association_rules中
'''
if len(freq_item) >= 2: # 遍历二阶及以上的频繁项集
for i in range(1, len(freq_item)): # 生成多种关联规则
for item in combinations(freq_item, i): # 遍历长度为1的item的组合
conf = support_data[frozenset(freq_item)] / float(support_data[frozenset(freq_item) - frozenset(item)])
if conf >= min_confd:
association_rules.append((freq_item - set(item), item, conf))
gen_rules(freq_item - set(item), support_data, min_confd, association_rules)
def support_map(freq_item_set, item_set_support):
'''
将生成的频繁项集和每个项集对应的支持度对应起来
Returns:
--------
support_data: {frozenset(item1, item2..): support_score, ..}
'''
support_data = {}
for i in range(len(freq_item_set)):
for j in range(len(freq_item_set[i])):
support_data[frozenset(freq_item_set[i][j])] = item_set_support[i][j]
return support_data
def apriori_gen_rules(data_set, min_support, min_confd):
'''
利用apriori算法生成关联规则分为两步:
Step1:生成频繁项集
Step2:生成关联规则
Parameters:
-----------
data_set: item list
min_support: 项集需要满足的最小支持度,|X U Y| / |All|
min_confd: 项集之间关系需要满足的最小置信度,|X U Y| / |X|
Returns:
--------
rules: 通过apriori算法挖掘出的关联规则
'''
freq_item_set, item_set_support = gen_frequecy_set(data_set, min_support) # 利用Apriori算法生成频繁项集和对应的支持度
support_data = support_map(freq_item_set, item_set_support) # 将频繁项集和支持度联系起来
rules = gen_association_rules(freq_item_set, support_data, min_confd) # 利用频繁项集、对应的支持度和置信度生成关联规则
return rules
if __name__ == '__main__':
data_set = readdata("DATA.txt")
min_support = 0.2 # 最小支持度
min_confd = 0.4 # 可信度或支持度
rules = apriori_gen_rules(data_set=data_set, min_support=min_support, min_confd=min_confd)
print(sorted(rules, key=lambda x: x[2], reverse=True))
?文末资源推荐
🍓 🍑 🍈 🍌 🍐 🍍 🍠 🍆 🍅 🌽
点击下方即可下载 ??????????
Python爬取知网论文信息,包含数据爬取、数据分析、数据可视化代码
每文一语
爱不释手,才是爱的意义