开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 大数据 -> 从数据库库索引说到空间数据索引 -> 正文阅读

[大数据]从数据库库索引说到空间数据索引

要说空间索引，我们不得不先说一下数据库索引。

1. 数据库索引

1.1. 什么是数据库索引

索引是定义在table基础之上，有助于无需检查所有记录而快速定位所需记录的一种辅助存储结构，由一系列存储在磁盘上的索引项组成，每一种索引项由索引字段和行指针构成。

1.2. 数据索引是干什么用的呢？

数据库索引其实就是为了使查询数据效率快。

1.3. 索引的好处？

通过创建索引,可以在查询的过程中,提高系统的性能；
通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性；
在使用分组和排序子句进行数据检索时,可以减少查询中分组和排序的时间；

1.4. 索引的坏处？

创建索引和维护索引要耗费时间,而且时间随着数据量的增加而增大；
索引需要占用物理空间,如果要建立聚簇索引,所需要的空间会更大；
在对表中的数据进行增加删除和修改时需要耗费较多的时间,因为索引也要动态地维护；

1.5. 何时创建索引?

表的主键和包含唯一约束的列自动创建索引，所以在建立唯一约束时，可以考虑该列是否必要建立，是否要作为查询条件。
如果某个表的数据量较大（十几二十万以上），某列经常作为where的查询条件，并且检索的出来的行数经常是小于总表的5%，那该列可以考虑建立索引。
对于两表连接的字段，应该考虑建立索引。如果经常在某表的一个字段进行Order By 则也经过进行索引。

1.6. 为什么索引能提高查询速度?

https://baijiahao.baidu.com/s?id=1644431964707531789&wfr=spider&for=pc

2. 空间索引

????????空间索引是指依据空间对象的位置和形状或空间对象之间的某种空间关系按一定的顺序排列的一种数据结构，其中包含空间对象的概要信息，如对象的标识、外接矩形及指向空间对象实体的指针。

????????空间数据查询即空间索引，是对存储在介质上的数据位置信息的描述，是用来提高系统对数据获取的效率，也称为空间访问方法(Spatial Access Method SAM)。是指依据空间对象的位置和形状或空间对象之间的某种空间关系按一定的顺序排列的一种数据结构其中包含空间对象的概要信息如对象的标识外接矩形及指向空间对象实体的指针。

????????作为一种辅助性的空间数据结构空间索引介于空间操作算法和空间对象之间它通过筛选作用大量与特定空间操作无关的空间对象被排除从而提高空间操作的速度和效率。

2.1. 常见的空间索引

????????常见空间索引类型有BSP树、K－D－B树、R树、R+树和CELL树，空间索引的性能的优越直接影响空间数据库和地理信息系统的整体性能。结构较为简单的格网型空间索引在各GIS软件和系统中（如ArcGIS）都有着广泛的应用。

2.1.1. 基于网格的空间索引

????????网格索引的基本思想是将研究区域按一定规则用横竖线分为小的网格，记录每个网格所包含的地理对象。当用户进行空间查询时，首先计算查询对象所在的网格，然后通过该网格快速查询所选的地理对象。网格索引算法大致分为三类：基于固定网格划分的空间索引算法、基于多层次网格的空间索引算法和自适应层次网格空间索引算法。

基于固定网格的空间索引

????????将一幅地图分割成ab的固定网格，再根据一定的方法将网格编码，为落入每个格网内的地图目标建立索引，这样只需检索原来区域的1/ab，以达到快速检索的目的。该算法的优点是操作简单，在涉及的数据量不大、不需要进行复杂操作时具有一定的适应性。例如对点对象的检索特点适合使用。

在这里插入图片描述
例如面的网格索引

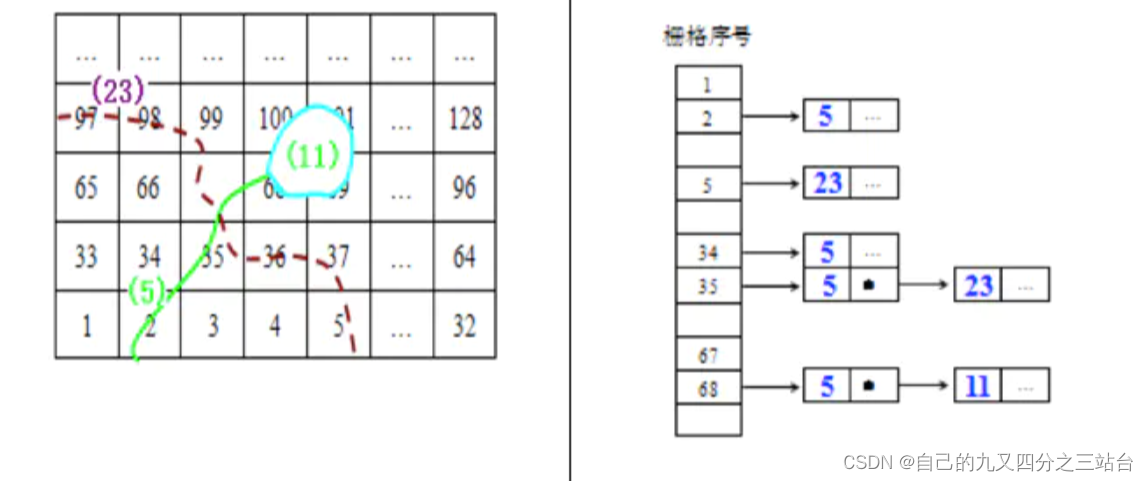
在这里插入图片描述

2.1.2. 四叉树空间索引

????????具体可以借鉴博客：https://blog.csdn.net/zhouxuguang236/article/details/12312099

????????四叉树索引可能是最早的专门为存取空间数据而设计的数据结构，不仅可用于二维变量，也可以用于任意维数。它是二叉树用于二维数据的一种推广。

????????四叉树索引，类似于网格索引，也是对地理空间进行网格划分，对地理空间递归进行四分来构建四叉树，直到自行设定的终止条件（比如每个节点关联图元的个数不超过3 个，超过 3 个，就再四分），最终形成一颗有层次的四叉树。它的特点如下
1. 每个叶子节点存储了本区域所关联的图元标识列表和本区域地理范围；
2. 非叶子节点仅存储本区域地理范围。

????????由于四叉树的生成和维护比较简单，且当空间数据对象分布比较均匀时，基于四叉树的空间索引可以获得比较高的空间数据插入和查询效率。如下两图：

在这里插入图片描述

2.1.3. KD树

????????K邻近算法在这里就不提及了，KD树（K维搜索树）是把二叉树推广到多维数据的一种主存数据结构，它是一个K维空间中的平衡二叉树，主要用于存储点数据。在每一个内部节点中，它用一个k-1维的超平面（如二维空间的线）将节点所表示的k维空间分成两个部分，这些超平面在k个可能的方向上交替出现，而且在每一个超平面中至少包括一个点数据。在KD树中查找一个所有维都给定值得对象的处理如同在二叉树中一样，只需在每个内部节点上决定沿哪个走向，直至搜索到叶节点为止。

????????假设有6个二维数据点{(2,3)，(5,4)，(9,6)，(4,7)，(8,1)，(7,2)}，数据点位于二维空间内，如下图八所示。为了能有效的找到最近邻，kd树采用分而治之的思想，即将整个空间划分为几个小部分。首先，粗黑线将空间一分为二，然后在两个子空间中，细黑直线又将整个空间划分为四部分，最后虚黑直线将这四部分进一步划分。

2.1.4. KDB树

????????KDB树兼有KD树和B树的特性，以B树的方式进行插入和删除，是完全平衡的，且可以进行局部重组，她的主要缺陷是不能保证最小空间利用率。KDB树是B树享多味空间发展的一种形式。它对于多维空间中的点进行索引，具有较好的动态特性，删除和增加地理要素可以很方便地实现。其缺点是不直接支持占据一定空间范围的地理要素，如2维空间中的线和面。

2.1.5. BSP树

????????BSP表示二叉空间分割，BSP树能很好地与空间对象的分布情况相适应，但对一般情况而言，BSP树深度较大，对各种操作均有不利影响。

????????它的基本思想是基于这样一个事实，任何平面都可以将空间分割成两个半空间。所有位于这个平面的一侧的点定义了一个半空间，位于另一侧的点定义了另一个半空间。此外，如果我们在任何半空间中有一个平面，它会进一步将此半空间分割为更小的两个子空间。我们可以使用多边形列表将这一过程一直进行下去，将子空间分割得越来越小，直到构造成一个二叉树。在这个树中，一个进行分割的多边形被存储在树的节点，所有位于子空间中的多边形都在相应的子树上。当然，这一规则使用于树中每一个节点。

2.1.6. R树空间索引

????????具体可借鉴博客：https://blog.csdn.net/jazywoo123/article/details/7792745

????????R树是B树向多维空间发展的另一种形式，它将空间对象按范围划分，每个结点都对应一个区域和一个磁盘页，非叶结点的磁盘页中存储其所有子结点的区域范围，非叶结点的所有子结点的区域都落在它的区域范围之内；叶结点的磁盘页中存储其区域范围之内的所有空间对象的外接矩形。每个结点所能拥有的子结点数目有上、下限，下限保证对磁盘空间的有效利用，上限保证每个结点对应一个磁盘页，当插入新的结点导致某结点要求的空间大于一个磁盘页时，该结点一分为二。R树是一种动态索引结构，即：它的查询可与插入或删除同时进行，而且不需要定期地对树结构进行重新组织。

????????在构造R 树时，要求虚拟矩形之间尽量不要相互重叠，而且一个空间实体通常仅被一个同级虚拟矩形所包围。但由于空间对象的复杂性，虚拟矩形难免重叠。R+树是对R 树索引的一种改进，它允许虚拟矩形可以相互重叠，并分割下层虚拟矩形，允许一个空间实体被多个虚拟矩形包围。在构造虚拟矩形时，尽量保持每个虚拟矩形包含相同个数的下层虚拟矩形或实体外接矩形，以保证任一实体具有相近的检索时间。

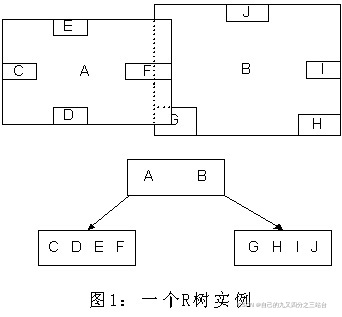
在这里插入图片描述

2.1.7. R+树空间索引

????????在Guttman的工作的基础上，许多R树的变种被开发出来， Sellis等提出了R+树，R+树与R树类似，主要区别在于R+树中兄弟结点对应的空间区域无重叠，这样划分空间消除了R树因允许结点间的重叠而产生的“死区域”（一个结点内不含本结点数据的空白区域），减少了无效查询数，从而大大提高空间索引的效率，但对于插入、删除空间对象的操作，则由于操作要保证空间区域无重叠而效率降低。同时R+树对跨区域的空间物体的数据的存储是有冗余的，而且随着数据库中数据的增多，冗余信息会不断增长。Greene也提出了他的R树的变种。

2.1.8. R*树

????????在1990年，Beckman和Kriegel提出了最佳动态R树的变种——R树。R树和R树一样允许矩形的重叠，但在构造算法R树不仅考虑了索引空间的“面积”，而且还考虑了索引空间的重叠。该方法对结点的插入、分裂算法进行了改进，并采用“强制重新插入”的方法使树的结构得到优化。但R树算法仍然不能有效地降低空间的重叠程度，尤其是在数据量较大、空间维数增加时表现的更为明显。R*树无法处理维数高于20的情况。

2.2.9. QR树

????????QR树利用四叉树将空间划分成一些子空间，在各子空间内使用许多R树索引，从而改良索引空间的重叠。QR树结合了四叉树与R树的优势，是二者的综合应用。实验证明：与R树相比，QR树以略大（有时甚至略小）的空间开销代价，换取了更高的性能，且索引目标数越多，QR树的整体性能越好。

3.空间索引简单对比

索引名称	空间对象的集合构造近似方法	划分方法	是否转化	是否支持二叉树	优点	缺点
B树	数据分层	数据分层	否	支持	高效、动态索引	无法胜任海量数据
R树	矩形	空间对象	否	支持	比KD树和四叉树灵活，单是查询效率高	区域重叠，难以动态维护
R变种树	矩形或不规则多边形	空间对象	否	支持	解决R树区域重叠，插入难得问题	算法复杂，难以动态维护
BSD树	按对象二分	空间对象	是	不支持	运行的复杂性较低，区域无重叠，查询高效	空间复杂度大，难以动态维护
网格索引	面积等分或不等分	空间对象	是	支持	算法简单，结合编码，查询高效	数据冗余大，变长记录，难以动态维护
四叉树	面积四分	空间对象	是	支持	空间划分无重叠，隐含空间关系，查询快	深度大，数据结构复杂，难以动态维护
KD树	按点二分	点对象	否	不支持	具有较低的存储需求，高效查询	无法管理海量数据，更新困难，适用于点对象索引
KDB树	按点二分	点对象	否	不支持	动态索引、高效查询	删除算法效率低，空间复杂度大，主要用于点对象管理

4. PostGis的通用搜索树

数据库对多维数据的存取有两种索引方案，R-Tree和GIST（Generalized Search Tree）简称“通用搜索树”，在PostgreSQL中的GiST比R-Tree的健壮性更好，因此PostGIS对空间数据的索引一般采用GiST实现。

通用搜索树是一棵平衡树，其特点如下：

除根节点的扇出数在2和M之间外，每个节点的扇出数在kM和M之间，这里2/M<=k<=1/2。常量k称作该树的最小填充因子，M为一个节点可以容纳索引项的最大数目。
索引项形式为（p，ptr），其中p是用作搜索码的谓词（谓词中可以包含自由变量，只要相应子树中叶节点标识的所有元组能实例化这些变量即可）。在叶节点中，ptr为指向数据库中某一元组的指针；而在非叶结点中，ptr为指向其子树根结点的指针。

它是一种可扩展的树型索引结构框架。这里的“可扩展”包含层意思：一是支持数据类型的可扩展性；二是支持查询谓词的可扩展性。

4.1. GIST通用搜索树

4.1.1. Gist索引的使用场景有哪些。

因为gist是一个通用的索引接口，所以可以使用GiST实现b-tree, r-tree等索引结构。
不同的类型，支持的索引检索也各不一样。例如：
1、几何类型，支持位置搜索（包含、相交、在上下左右等），按距离排序。
2、范围类型，支持位置搜索（包含、相交、在左右等）。
3、IP类型，支持位置搜索（包含、相交、在左右等）。
4、空间类型（PostGIS），支持位置搜索（包含、相交、在上下左右等），按距离排序。
5、标量类型，支持按距离排序。

可以借鉴：
https://blog.csdn.net/weixin_39540651/article/details/105998418?utm_medium=distribute.pc_relevant.none-task-blog-2_defaultbaidujs_title~default-1.pc_relevant_antiscan&spm=1001.2101.3001.4242.2&utm_relevant_index=4

https://blog.csdn.net/dazuiba008/article/details/104517679?utm_medium=distribute.pc_relevant.none-task-blog-2_defaultbaidujs_baidulandingword~default-0.queryctrv4&spm=1001.2101.3001.4242.1&utm_relevant_index=3

4.1.1.1 几何类型检索

创建一个存放几何数据的表：

create table t_gist (id int, pos point);    

insert into t_gist select generate_series(1,100000), point(round((random()*1000)::numeric, 2), round((random()*1000)::numeric, 2));   

select * from t_gist limit 5;

 id |       pos       
----+-----------------
  1 | (614.87,412.97)
  2 | (248.71,779.61)
  3 | (976.17,826.79)
  4 | (999.39,126.9)
  5 | (651.61,364.49)
(5 rows)

在pos列上创建gist索引：

create index idx_t_gist_1 on t_gist using gist (pos);

可以发现gist索引支持bitmap scan和index scan

explain (analyze,verbose,timing,costs,buffers) select * from t_gist where circle '((100,100) 10)'  @> pos;    
                                                       QUERY PLAN                                                       
------------------------------------------------------------------------------------------------------------------------
 Bitmap Heap Scan on bill.t_gist  (cost=2.35..113.84 rows=100 width=20) (actual time=0.107..0.157 rows=35 loops=1)
   Output: id, pos
   Recheck Cond: ('<(100,100),10>'::circle @> t_gist.pos)
   Heap Blocks: exact=32
   Buffers: shared hit=38
   ->  Bitmap Index Scan on idx_t_gist_1  (cost=0.00..2.33 rows=100 width=0) (actual time=0.093..0.093 rows=35 loops=1)
         Index Cond: (t_gist.pos <@ '<(100,100),10>'::circle)
         Buffers: shared hit=6
 Planning Time: 0.188 ms
 Execution Time: 0.268 ms
(10 rows)

explain (analyze,verbose,timing,costs,buffers) select * from t_gist where circle '((100,100) 1)' @> pos order by pos <-> '(100,100)' limit 10; 
                                                             QUERY PLAN                                                              
-------------------------------------------------------------------------------------------------------------------------------------
 Limit  (cost=0.28..12.72 rows=10 width=28) (actual time=0.084..0.085 rows=1 loops=1)
   Output: id, pos, ((pos <-> '(100,100)'::point))
   Buffers: shared hit=4
   ->  Index Scan using idx_t_gist_1 on bill.t_gist  (cost=0.28..124.73 rows=100 width=28) (actual time=0.082..0.083 rows=1 loops=1)
         Output: id, pos, (pos <-> '(100,100)'::point)
         Index Cond: (t_gist.pos <@ '<(100,100),1>'::circle)
         Order By: (t_gist.pos <-> '(100,100)'::point)
         Buffers: shared hit=4
 Planning Time: 0.175 ms
 Execution Time: 0.129 ms
(10 rows)

4.1.1.2 标量类型

因为gist可以实现btree的索引结构，所以我们也可以在例如数字这种标量类型上使用gist索引(虽然一般都不如btree索引效果好)，不过我们还需要使用btree_gist索引插件。

create extension btree_gist ;

create table t_btree(id int,info text);

insert into t_btree select generate_series(1,100000),md5(random()::text);

create index idx_t_btree on t_btree using gist(id);

explain (analyze,verbose,timing,costs,buffers) select * from t_btree order by id <-> 100 limit 1;
                                                               QUERY PLAN                                                                
-----------------------------------------------------------------------------------------------------------------------------------------
 Limit  (cost=0.28..0.32 rows=1 width=41) (actual time=0.072..0.073 rows=1 loops=1)
   Output: id, info, ((id <-> 100))
   Buffers: shared hit=4
   ->  Index Scan using idx_t_btree on bill.t_btree  (cost=0.28..3798.18 rows=100000 width=41) (actual time=0.071..0.071 rows=1 loops=1)
         Output: id, info, (id <-> 100)
         Order By: (t_btree.id <-> 100)
         Buffers: shared hit=4
 Planning Time: 0.334 ms
 Execution Time: 0.118 ms
(9 rows)

4.1.2. 总结

????????Gist索引实现首先要将数据聚集，聚集后，在单个组内包含的KEY+HEAP行号会放到单个INDEX PAGE中。
????????聚集的范围作为一级结构，存储在GiST的entry 中，便于检索。
????????既然灵魂是聚集，那么GiST的性能就和他的聚集算法息息相关，PostgreSQL把这个接口留给了用户，用户在自定义数据类型时，如果要自己实现对应的GIST索引，那么就好好考虑这个类型聚集怎么做吧。
????????PostgreSQL内置的range, geometry等类型的GIST已经帮你做好了，你只需要做新增的类型，比如你新增了一个存储人体结构的类型，存储图片的类型，或者存储X光片的类型，怎么快速检索它们，那就是你要实现的GIST索引聚集部分了。

5. 参考链接：

https://baijiahao.baidu.com/s?id=1644431964707531789&wfr=spider&for=pc

https://blog.csdn.net/zhouxuguang236/article/details/12312099

https://blog.csdn.net/jazywoo123/article/details/7792745

https://blog.csdn.net/weixin_39540651/article/details/105998418?utm_medium=distribute.pc_relevant.none-task-blog-2_defaultbaidujs_title~default-1.pc_relevant_antiscan&spm=1001.2101.3001.4242.2&utm_relevant_index=4

https://habr.com/ru/company/postgrespro/blog/444742/

https://www.cnblogs.com/cmi-sh-love/p/kong-jian-shud-ju-suo-yinRTree-wan-quan-jie-xi-jiJa.html

https://github.com/digoal/blog/blob/master/201906/20190604_03.md

scan&spm=1001.2101.3001.4242.2&utm_relevant_index=4

https://habr.com/ru/company/postgrespro/blog/444742/

https://www.cnblogs.com/cmi-sh-love/p/kong-jian-shud-ju-suo-yinRTree-wan-quan-jie-xi-jiJa.html

https://github.com/digoal/blog/blob/master/201906/20190604_03.md