[大数据]秋招备战之MySQL索引

一、什么是索引：

索引是mysql的一种数据结构,这种数据结构称之为 key,或者说是一种数据的组织方式
表中的一行行数据按照索引规定的结构组织成了一种树形结构，该树叫B+树

范围查询其实相当于n次等值查询
范围索引:select name where id>3
等值索引:select name where id=2

二、为何要用索引：

优化查询速度，对于数据库来说读（select）写(insert,update,delete)比例就是十：一，所以查的优化就显得很重要
?

三、如何正确看待索引：

错误的认知：
? ? 1、软件上线之后，运行了一段时间，发现软件运行非常卡，想要加索引
? ? ? ? --》软件慢不一定是数据库慢，上线之后加也晚了（软件上线前加索引），光把问题定位到索引身上就需要耗费很长时间，排查成本高
? ? ? ? 解决办法：在软件上线之出配合开发人员，定位到常用的查询字段，然后为该字段创建索引

? ? 2、索引越多越好
? ? ? ? --》索引是用于加速查询的，会降低写的效率
? ? ? ? --》每建一个索引就是构建了一条索引树，索引结构的一些数据存在ibd文件内，而文件占硬盘空间，也意味着很小的一个update语句就会导致很多课索引树都需要发生变化，从而把硬盘IO打上去
?

四、储备知识

1、索引的根本原理就是把硬盘的IO次数降下来
2、为一张表中的一行行记录创建索引，就是为书的一页页内容创建目录，有了目录结构后，我们以后的查询都应该通过目录去查询
3、一次磁盘IO带来的影响：
? ? 假设磁盘：7200转/m-> 120转/s
? ? 磁盘慢慢在找数据的速度上
? ? 一次IO的延迟时间=平均寻道时间（大概需要5ms）+ 平均延迟时间(转半圈的时间 4ms)=9ms
4、磁盘的预读
? ? 一页就是一个磁盘块
? ? innodb存储引擎一页16k,及一次io读16k到内存中
? ? 磁盘的预读的概念：当计算机访问一个地址的数据的时候，与其相邻的数据也会很快被访问到
?

五、索引分类

索引模型的分类：
? ? 1 B+树索引（等值查询与范围查询都快）
? ? 2 HASH索引（等值查询快，范围查询慢）
? ? 3 FULL TEXT 全文索引（只可以用在MYISAM引擎）
?

六、创建索引的两个步骤

? ? create index xx on user(id)
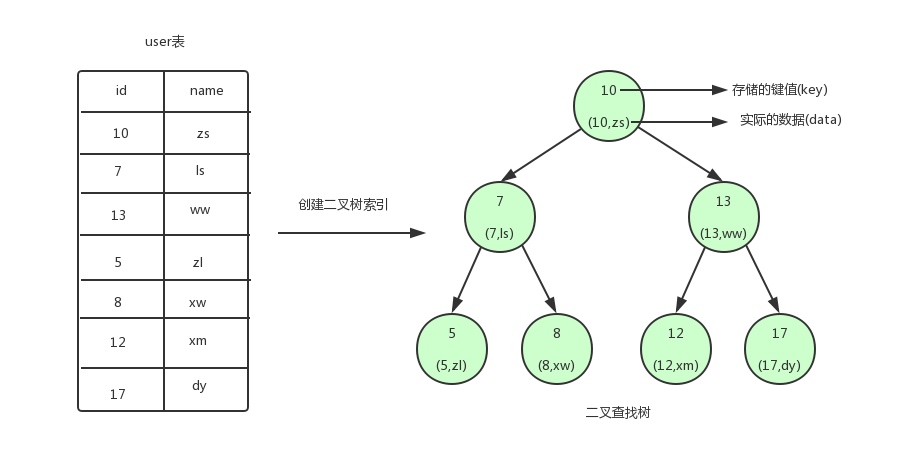
? ? 1 提取索引字段的值当作key,value就是对应的本行记录
? ? 假设有如下字段与数据
? ? id name
? ? 10 ?21
? ? 7 ? 15
? ? 14 ?ww
? ? 5 ? xx

? ? key:10-----》value:(10,21)
? ? ? ? 7 -----》value:(7,15)
? ? 2 以key的为基础比较大小，生成树形结构

七、B+树

? ? 演变：二叉查找树-》平衡二叉树-》B树-》B+树
? ? 1 二叉查找树的特点就是任何节点的左子节点的键值都小于当前节点的键值，右子节点的键值都大于当前节点的键值。

? ? 顶端的节点我们称为根节点，没有子节点的节点我们称之为叶节点。
? ? 当构建树形结构后查询次数和树的高度有关系
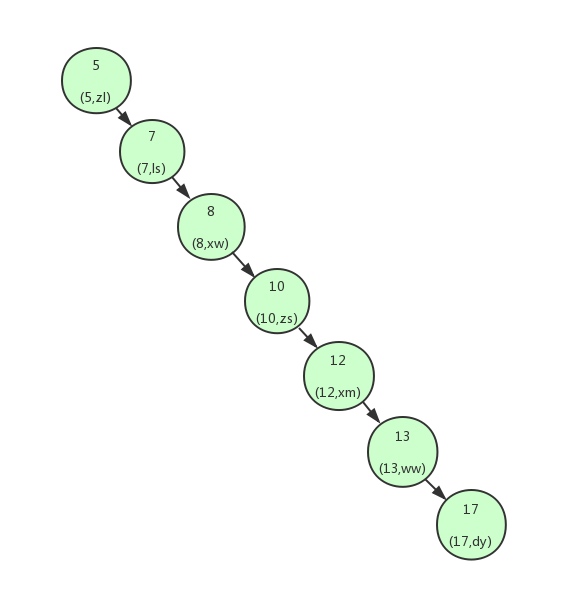
? ? 缺点：当二叉树变成一个链表时，就相当于全表扫描了

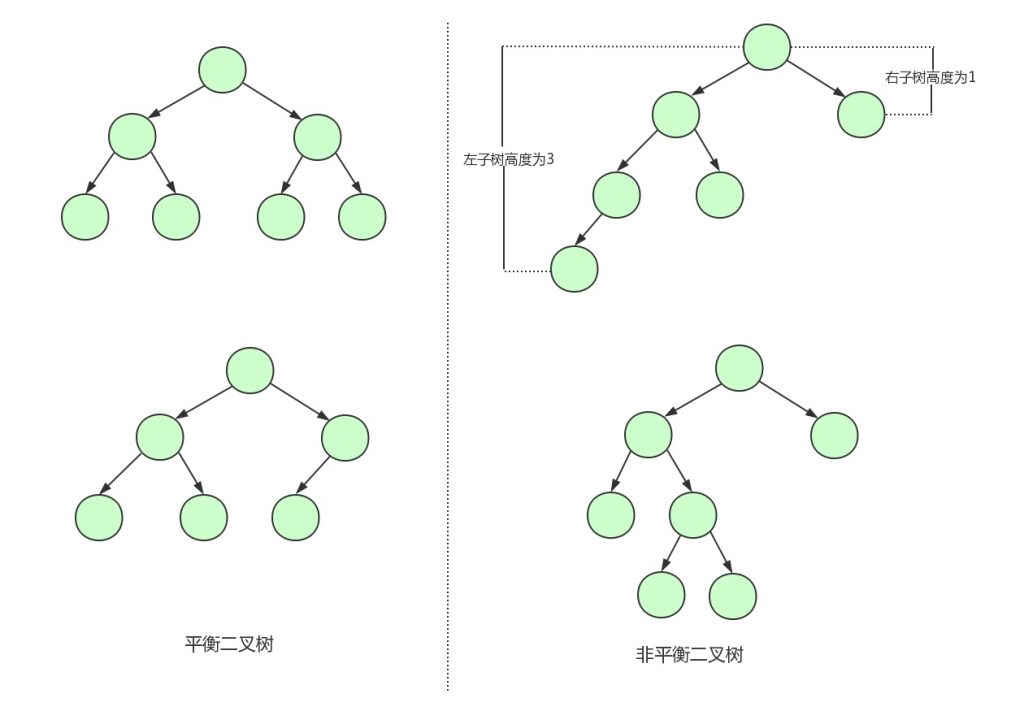
? ? 解决办法：导致这个现象的原因其实是二叉查找树变得不平衡了，也就是高度太高了，从而导致查找效率的不稳定。 为了解决这个问题，我们需要保证二叉查找树一直保持平衡，就需要用到平衡二叉树了

? ? 2 平衡二叉树 平衡二叉树又称AVL树，在满足二叉查找树特性的基础上，要求每个节点的左右子树的高度不能超过1

? ? 缺点：每个节点只放了一条数据
? ? 解决办法：如果我们能够在平衡二叉的树的基础上，把更多的节点放入一个磁盘块中，那么平衡二叉树的弊端也就解决了。即构建一个单节点可以存储多个键值对的平衡树，这就是B树。

? ? 3 B树 B树（Balance Tree）即为平衡树的意思，特点：一个磁盘块存入多个节点

? ? B树相对于平衡二叉树，每个节点存储了更多的键值(key)和数据(data)，并且每个节点拥有更多的子节点，子节点的个数一般称为阶
? ? 基于这个特性，B树查找数据读取磁盘的次数将会很少，数据的查找效率也会比平衡二叉树高很多
? ? ps:根节点是常驻内存的（根节点不需要读）
? ? 缺点：B树只擅长做等值查询，而对于范围查询（范围查询的本质就是n次等值查询），或者说排序操作，B树也帮不了我们

? ? 4 B+树 B+树是对B树的进一步优化

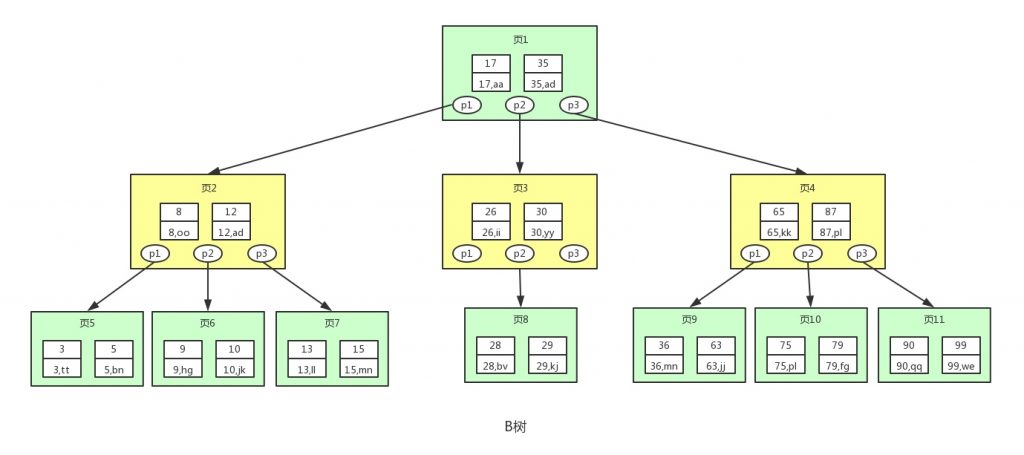
? ? B+树与B树的对比
? ? a B+树非叶子节点non-leaf node上是不存储数据的，仅存储键，
? ? 而B树的非叶子节点中不仅存储键，也会存储数据。B+树之所以这么做的意义在于：树一个节点就是一个页，而数据库中页的大小是固定的，innodb存储引擎默认一页为16KB，
? ? 所以在页大小固定的前提下，能往一个页中放入更多的节点，相应的树的阶数（节点的子节点树）就会更大，那么树的高度必然更矮更胖，如此一来我们查找数据进行磁盘的IO次数有会再次减少，数据查询的效率也会更快。

? ? b B+树的阶数是等于键的数量的
? ? 例如上图，我们的B+树中每个节点可以存储3个键，3层B+树存可以存储3*3*3=9个数据。
? ? 所以如果我们的B+树一个节点可以存储1000个键值，那么3层B+树可以存储1000×1000×1000=10亿个数据。而一般根节点是常驻内存的，所以一般我们查找10亿数据，只需要2次磁盘IO，真是屌炸天的设计。

? ? c 因为B+树索引的所有数据均存储在叶子节点leaf node，而且数据是按照顺序排列的。那么B+树使得范围查找，排序查找，分组查找以及去重查找变得异常简单。而B树因为数据分散在各个节点，要实现这一点是很不容易的。
而且B+树中各个页之间也是通过双向链表连接的，叶子节点中的数据是通过单向链表连接的。其实上面的B树我们也可以对各个节点加上链表。其实这些不是它们之前的区别，是因为在mysql的innodb存储引擎中，索引就是这样存储的。也就是说上图中的B+树索引就是innodb中B+树索引真正的实现方式，准确的说应该是聚集索引。

ps:创建索引时，ibd文件变大，但查询效率提高了，所以说索引是浪费空间换时间
?

八、B+树分类

ibd文件内不只一颗B+树
如：
create index xx on user(id); 以id为索引构建一个B+树
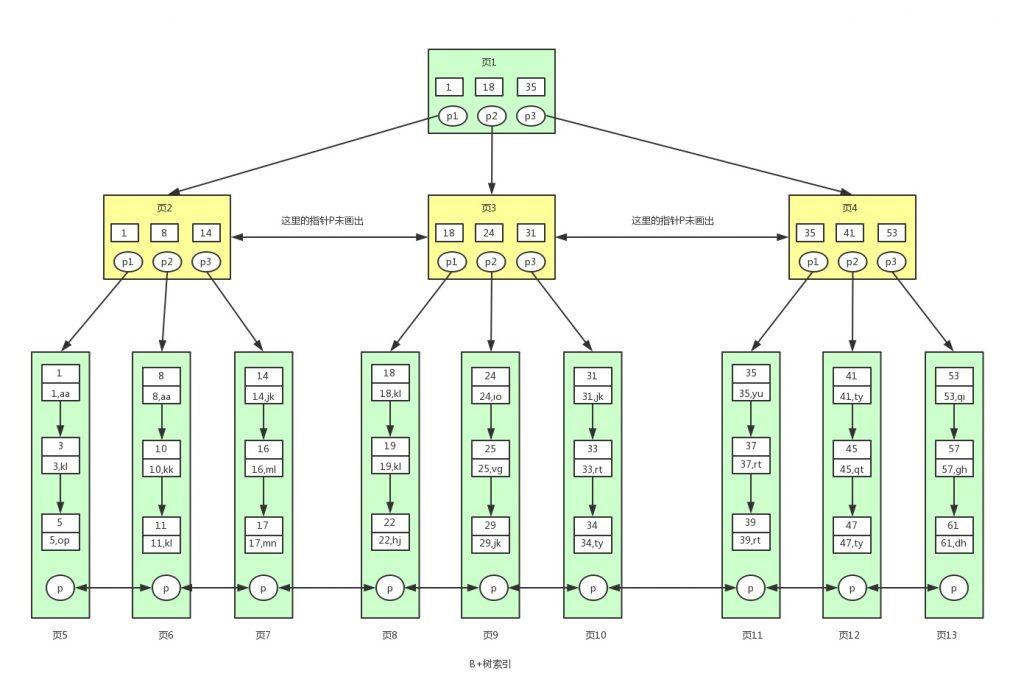
create index xx on user(name); 以name为索引构建一个B+树

第一类：多种叫法：聚集索引、聚簇索引、主键索引、一级索引
? ? 以主键为key值构建的B+树，该B+树的叶子节点放的是主键值与本行完整的记录，表中的数据都聚集在叶子节点中，所以称之为聚集索引
? ? create index yy on user(id)
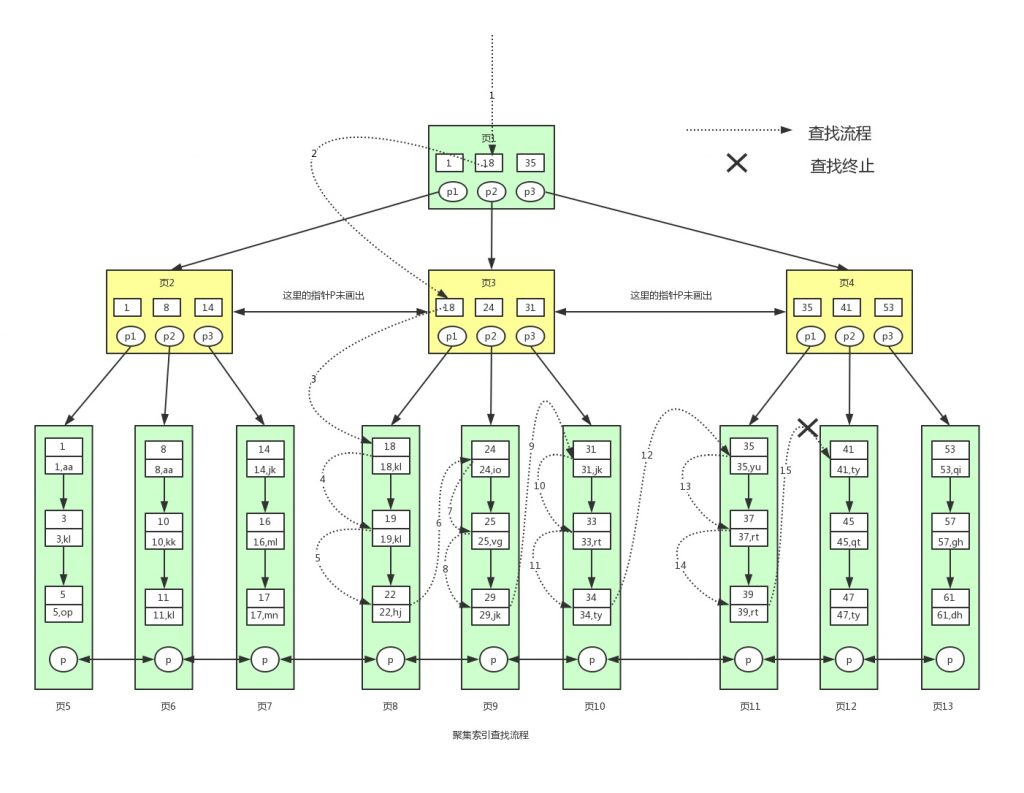
? ? select * from user where id='xx'

利用聚集索引查找数据

下面看下具体的查找流程图

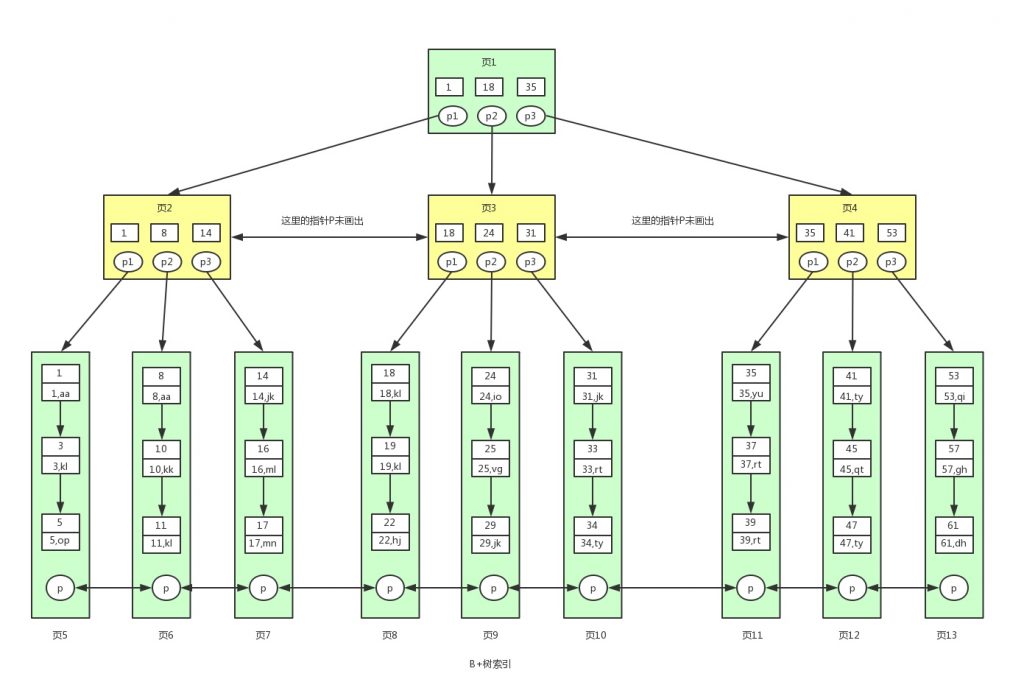
第二类：多种叫法：非聚集索引、非聚簇索引、辅助索引、二级索引
? ? 以非主键值当作key构建的B+树，该B+树的叶子节点存放的是key与其对应的主键字段值
? ? create index yy on user(name)
? ? select * from user where name='xx'

ps:1 innodb存储引擎一定有一个主键，若没创建主键，会从上到下找到一个不为空且唯一的字段当主键，若没有这样的字段，会创建一个隐藏字段为key值构建索引树
? ?2 一张innodb存储引擎表中必须要有只能有一个聚集索引，但是可以有多个辅助索引

利用非聚集索引查找

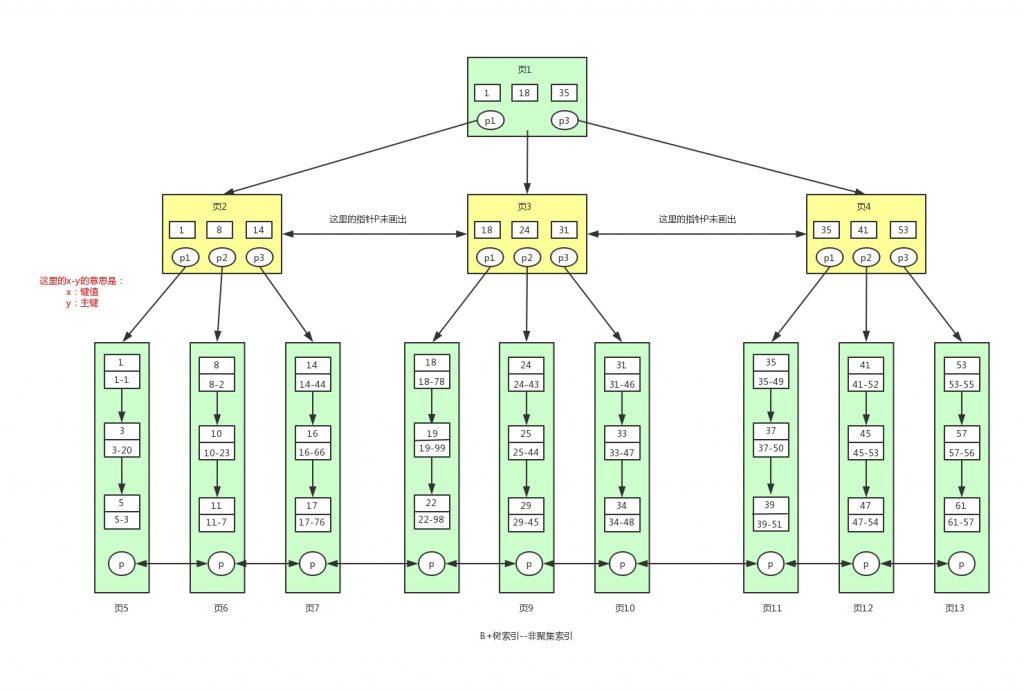
下面看下具体的查找流程图：

九、覆盖了索引、回表操作

覆盖了索引：在命中索引的基础上，只在本索引树的叶子节点就找到了我们想要的数据
? ? 假设：主键索引-》id字段
? ? ? ? ?辅助索引-》name字段

? ? ? ? ?select name,id from user where name='egon'->id与name都在辅助索引树的叶子节点中
? ? ? ? ?selec * from user where id='2'->user中的所有数据都在以id为基础构建的B+树的叶子节点中
回表操作：在命中了辅助索引的基础上，在辅助索引的叶子节点并没有找到想要的数据，需要拿到对应的主键字段值去聚集索引里面再找一下
? ? 假设：主键索引-》id字段
? ? ? ? ?辅助索引-》name字段

? ? ? ? ?select name,age,gender from user where name='egon'->age与gender不在辅助索引的叶子节点（name与name对应的id值）中

十、索引管理

聚集索引 -primary key
非聚集索引 -unique
? ? ? ? ?-index

create table t1(
? ? id int ,
? ? class_name varchar(20),
? ? name varchar(16),
? ? age int
)

创建主键索引
alter table t1 add primary key t1(id)
删除主键字段
alter table t1 drop primary key

创建唯一索引
alter table t1 add unique key t1(class_name)
删除唯一索引
alter table t1 drop index t1

创建普通索引
create index xx on t1(name)
删除普通索引
drop index xx on t1
?

十一、联合索引与最左前缀匹配原则

create index xx on t1(id,name) 以(id,name,age)为索引

查找条件中出现：
? ? id,name,age
? ? id,age
? ? id,name
? ? id
? ? 我的查询条件中涉及多个字段值，但是这多个字段值有个共性，都带着某一个字段时(放最左边)，可以建联合索引