[大数据]Spark_GraphX_2

1.PageRank

历史上，PageRank算法作为计算互联网网页重要度的算法被提出。PageRank是定义在网页集合上的一个函数，它对每个网页给出一个正实数，表示网页的重要程度，整体构成一个向量，PageRank值越高，网页就越重要，在互联网搜索的排序中可能就被排在前面。

直观上，一个网页，如果指向该网页的超链接越多，随机跳转到该网页的概率也就越高，该网页的PageRank值就越高，这个网页也就越重要。一个网页，如果指向该网页的PageRank值越高，随机跳转到该网页的概率也就越高，该网页的PageRank值就越高，这个网页也就越重要。PageRank值依赖于网络的拓扑结构，一旦网络的拓扑(连接关系)确定，PageRank值就确定。

• PR值计算公式：v’=αMv+(1-α)e

object PageRank {
  def main(args: Array[String]): Unit = {
    val spark = SparkSession.builder().master("local[*]").appName("graph").getOrCreate()
    val sc = spark.sparkContext
    val users = sc.makeRDD(Array(
      (1L, ("Alice", 28)),
      (2L, ("Bob", 27)),
      (3L, ("Charlie", 65)),
      (4L, ("David", 42)),
      (5L, ("Ed", 55)),
      (6L, ("Fran", 42))))
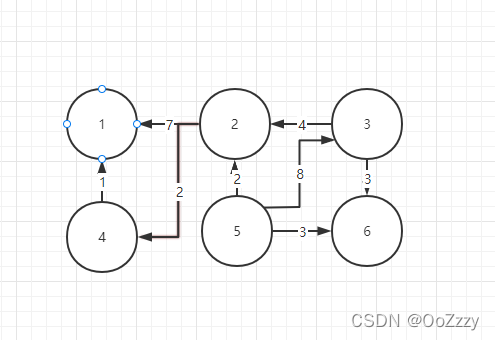
    val relationship = sc.makeRDD(Array(
      Edge(2L, 1L, 7),
      Edge(3L, 2L, 4),
      Edge(4L, 1L, 1),
      Edge(2L, 4L, 2),
      Edge(5L, 2L, 2),
      Edge(5L, 3L, 8),
      Edge(5L, 6L, 3),
      Edge(3L, 6L, 3)
    ))

    val graph = Graph(users, relationship)

    graph.pageRank(0.001).vertices.foreach(println)
  }
}

(2,0.9969646507526427)
(5,0.5451618049228395)
(1,1.7924127957615184)
(3,0.6996243163176441)
(6,0.9969646507526427)

算法: pageRank

2.Pregel

Pregel 是 Google 自 2009 年开始对外公开的图计算算法和系统， 主要用于解决无法在单机环境下计算的大规模图论计算问题。与其说 Pregel 是图计算的算法， 不如说它是一系列算法、模型和系统设计组合在一起形成的一套图模型处理方案。

Pregel算法一般用来求最短路径问题

图顶点的两个状态:

• 钝化状态：类似于休眠，激活状态的顶点若本轮迭代中未成功发送或接收消息的顶点在下次迭代中将变为钝化状态
• 激活状态：工作状态，每轮迭代都将尝试向周边顶点发送消息，钝化状态的顶点在成功接收消息后在下次迭代中将变为激活状态

过程:

1. 以顶点的属性值代表与起点的距离，所以初始给起点赋值为0，其余顶点赋值一个极大值。
2. 所有顶点起始状态为激活状态
3. 以边的属性代表src到dst的距离，消息发送成功的标准为发送端属性与边属性之和小于接受端属性。
4. 接收端接收到消息后，会更新自己的属性值
5. 第一轮遍历后，由于除起点外其他顶点属性值均为极大值，只有起点和起点能直接到达的点处于激活状态，其他顶点切换至钝化状态
6. 多轮迭代中，起点和靠近起点的顶点将逐渐进行钝化状态，远离起点的顶点将进入激活状态
7. 最终，所有顶点都将进入钝化状态，当所有顶点进入钝化状态后，计算结束。此时所有顶点的属性值即为到起点的距离

object PregelTest{
  def main(args: Array[String]): Unit = {
    val spark = SparkSession.builder().master("local[*]").appName("graph").getOrCreate()
    val sc = spark.sparkContext
    val users = sc.makeRDD(Array(
      (1L, ("Alice", 28)),
      (2L, ("Bob", 27)),
      (3L, ("Charlie", 65)),
      (4L, ("David", 42)),
      (5L, ("Ed", 55)),
      (6L, ("Fran", 42))))
    val relationship = sc.makeRDD(Array(
      Edge(2L, 1L, 7),
      Edge(3L, 2L, 4),
      Edge(4L, 1L, 1),
      Edge(2L, 4L, 2),
      Edge(5L, 2L, 2),
      Edge(5L, 3L, 8),
      Edge(5L, 6L, 3),
      Edge(3L, 6L, 3)
    ))

    val graph = Graph(users, relationship)

    val srcVertex = 5L
    // 首先将起始点的属性改为0
    val initGraph = graph.mapVertices {
      case (vid, (name, age)) =>
        if (vid == srcVertex) 0.0 else Double.PositiveInfinity
    }

    val pregelGraph = initGraph.pregel(
      Double.PositiveInfinity,
      Int.MaxValue,
      EdgeDirection.Either // 按边的方向发送消息，OUT和EITHER都可以，不可以设置为IN和BOTH
    )(
      (_: VertexId, vd: Double, disMsg: Double) => math.min(vd, disMsg), 
      (edgeTriplet: EdgeTriplet[Double, PartitionID]) => {
        if (edgeTriplet.srcAttr + edgeTriplet.attr < edgeTriplet.dstAttr) {
          Iterator[(VertexId, Double)]((edgeTriplet.dstId, edgeTriplet.srcAttr + edgeTriplet.attr))
        } else Iterator.empty
      },
      (msg1: Double, msg2: Double) => math.min(msg1, msg2)
    )
    pregelGraph.vertices.foreach(println)
  }
}

(5,0.0)
(4,4.0)
(6,3.0)
(2,2.0)
(3,8.0)
(1,5.0)

Pregel: Pregel