通常我们会遇到要判断一个元素是否在某个集合中的业务场景,一般想到的是将集合中所有元素保存起来,然后通过比较确定。
链表、树、散列表(又叫哈希表,HashTable)等等数据结构都是这种思路。
但是随着集合中元素的增加,我们需要的存储空间也会呈现线性增长,最终达到瓶颈。同时检索速度也越来越慢,上述三种结构的检索时间复杂度分别为O(n),O(long),O(1)。
这个时候布隆过滤器(Bloom Filter)就应云而生。
布隆过滤器介绍:布隆过滤器BloomFilter实际上是一个很长的二进制数组+一系列随机hash算法映射函数,主要用于判断一个元素是否在集合中。

布隆过滤器特点:
- 高效的插入和查询,占用空间少,返回的结果时不确定性的。
一个元素如果判断结果为存在的时候元素不一定存在,但是判断结果为不存在的时候则一定不存在。- 布隆过滤器可以添加元素,但是不能删除元素,删除元素会导致误判率增加。
- 误判只会发生在布隆过滤器没有添加过的元素,对于添加过的元素不会发生误判。
使用场景:
解决缓存穿透问题
缓存穿透: Redis和数据库都不存在,每次查询都要访问数据库。
使用布隆过滤器解决缓存穿透问题: 把已存在数据的key存在布隆过滤器中,相当于Redis前面挡着一个布隆过滤器。当有新的请求时,先到布隆过滤器中查询是否存在,如果布隆过滤器中不存在该条数据则直接返回,如果布隆过滤器中存在,再去查询Redis,如果Redis中没有查询到则去查询数据库。
黑名单校验
发现存在黑名单中的,就执行特定操作。比如:识别垃圾邮件,只要是邮箱在黑名单中的邮件,就识别为垃圾邮件。假设黑名单的数据是数以亿记的,存放起来就非常耗费存储空间的,布隆过滤器则是一个较好的解决方案。把所有黑名单都放在布隆过滤器中,在收到邮件时,判断邮件地址是否再布隆过滤器中即可。
布隆过滤器原理
布隆过滤器(Bloom Filter)是一种专门用来解决去重问题的高级数据结构。
实质就是一个大型位数组和几个不同的无偏hash函数(无偏标识分布均匀)。由一个初值都为0的bit数组和多个哈希函数构成,用来判断某个数据是否存在。但是跟HyperLogLog一样,它也一样有那么一点点不精确,也存在一定的误判概率。
添加key时
使用多个hash函数对key进行hash运算得到一个整数索引值,对位数组长度进行取模运算得到一个位置,每个hash函数都会得到一个不同的位置,将这几个都设置1就完成了add操作。
查询key
只要查询有其中一位是0就表示这个key不存在,但如果都是1,
则不一定存在对应的key.
结论:有,是可能有;无,是一定为。
当有变量被加入集合时,通过N个映射函数将这个变量映射成位图中的N个点,把他们设置为1(假设有两个变量都通过3个映射函数)。
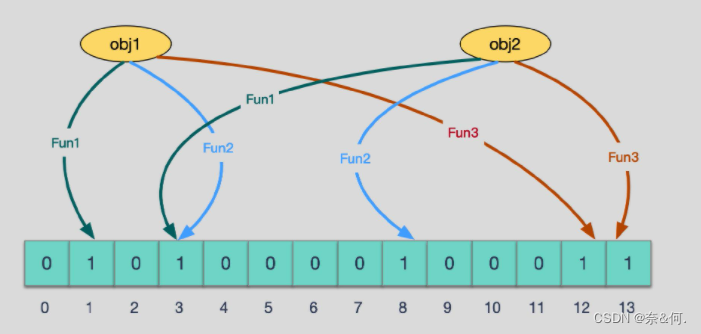
查询某个变量的时候我们只需要看看这些点是不是都是1,就可以大概率知道集合中有没有它了。如果这些点,有任何一个为0则被查询的变量不存在,如何都是1,则被查询的变量很可能存在。
为什么说是可能存在,而不是一定存在呢? 因为映射函数本身就是散列函数,散列函数是会发生碰撞的。
正事基于布隆过滤器的快速检测特性,我们可以在把数据写入数据库时,使用布隆过滤器做个标记。当缓存缺失后,应用查询数据库时,可以通过查询布隆过滤器快速判断数据是否存在。如果不存在,就不用再去数据库中查询了。这样一来,即使发生缓存穿透,大量的请求只会查询Redis和布隆过滤器,而不会积压到数据库,也就不会影响数据的正常运行。布隆过滤器可以使用Redis实现,本身就能承担较大的并发访问压力。
布隆过滤器的误判率,为什么删除后会增加误判率
布隆过滤器的误判是指多个输入经过哈希之后在相同的bit位设置1了,这样就无法判断究竟是那个输入产生的,因此误判的根源在于相同的bit位被多次映射且设置为1。
这种情况也造成了布隆过滤器的删除问题,因为布隆过滤器的每一个bit并不是独占的,很有可能多个元素共享了某一位。如果我们直接删除这一位的话,会影响其他的元素。
布隆过滤器特性:
- 一个元素判断结果为没有时则一定没有,如果判断结果为存在的时候元素不一定存在。
- 布隆过滤器可以添加元素,但是不能删除元素,因为删除元素会导致误判率增加。
