[嵌入式]小技巧：虚拟数据 方便数学实验。基于stm32dsp

虚拟数据

很多时候，我们需要在单片机里面对ADC采集到的数据进行信号处理，比如DSP。这过程需要ADC先采集数据，再对采集到的数据进行处理，这种操作显然很不方便。这时我们可以用单片机自己虚拟数据，送给后续处理，来节省时间。

就像平时使用matlab进行数学实验一样，先虚拟数据，再进行运算。我平时C语言用的比matlab熟练，很多数学上的简单实验验证，我都是拿单片机进行运算验证，再配合串口上位机打印波形，方便且形象。

函数介绍

float32_t arm_sin_f32( float32_t x )

输入值：输入是按照弧度制。比如$\frac{\pi }{2}$

返回值：sin（x）的计算结果，范围（-1，1）

解释：这个函数是包含在DSP库里面的，需要先把DSP包含进来才可以使用。不知道怎么包含，可以看看我之前写的DSP包含。

基本的正弦

代码实现

用一个相对频率为3的正弦波。（这里的频率后面再做解释）
$$\begin{gathered} 数学表达式：data=sin(6\pi x) \\ 离散表达式：data[i]=sin(\frac{6\pi ?i}{num}) \end{gathered}$$

//data{]:用于存放产生的数据
//PI：也就是3.14159...，是DSP库里面设置好的变量，直接用就行
//num：总的数据数量。
for (i = 0; i < num; i++) //生成信号序列
{
    data[i] = 1 * arm_sin_f32(2 * PI * 3 * i / num);
}

理解

我们来理解一下这里产生的data数组。首先sin括号内的数值（相位），取值范围是0->6$\pi$，如果画出来，相当于有三个周期的正弦波。其次取值点数是num个，也就是说6$\pi$被分成了num个等份，相当于取了num个点。最后，他的幅度由前面的data[i]=后面的数决定，这里是1，说明幅度是1。

下面把波形打印出来，方便大家理解。

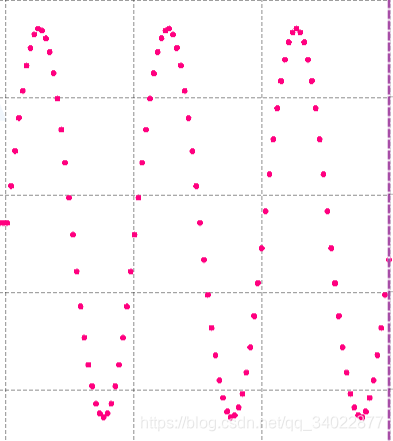
可以类推，2周期的幅度为3的正弦波，取10个点：
$$\begin{gathered} 数学表达式：data=3sin(4\pi x) \\ 离散表达式：data[i]=3sin(\frac{4\pi ?i}{num}) \end{gathered}$$

for (i = 0; i < 10; i++) //生成信号序列
{
    data[i] = 3 * arm_sin_f32(2 * PI * 2 * i / num);
}

波形如下：

2周期的幅度为3的正弦波，取1000个点：

for (i = 0; i < 1000; i++) //生成信号序列
{
    data[i] = 3 * arm_sin_f32(2 * PI * 2 * i / num);
}

波形如下：(点很多，已经连成线了，相较于上面的10个点，波形明显了不少)

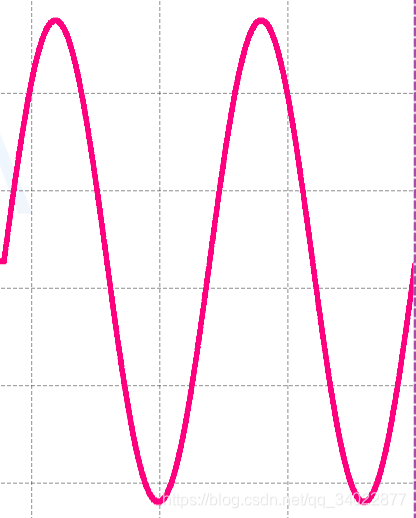
初始相位30°的正弦
$$\begin{gathered} 数学表达式：data=sin(4\pi x+\frac{\pi }{6}) \\ 离散表达式：data[i]=sin(\frac{4\pi ?i}{num}+\frac{\pi }{6}) \end{gathered}$$

for (i = 0; i < 1000; i++) //生成信号序列
{
    data[i] = 1 * arm_sin_f32(2 * PI * 2 * i / num + PI/6);
}

波形图如下：

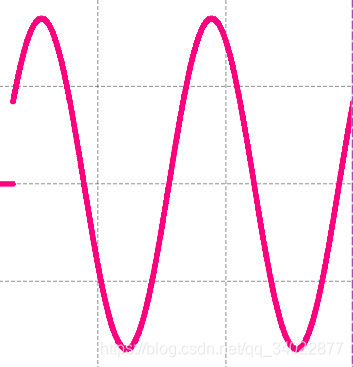
多次谐波信号

在理解了上面基本正弦的内容后，理解这一部分就不难了。
$$\begin{gathered} 数学表达式：data=2sin(6\pi x)+sin(10\pi x) \\ 离散表达式：data[i]=2sin(\frac{6\pi ?i}{num}) \end{gathered}$$

//data{]:用于存放产生的数据
//PI：也就是3.14159...，是DSP库里面设置好的变量，直接用就行
//num：总的数据数量。
for (i = 0; i < num; i++) //生成信号序列
{
    data[i] = 2 * arm_sin_f32(2 * PI * 3 * i / num)
    		+1 * arm_sin_f32(2 * PI * 5 * i / num);
}

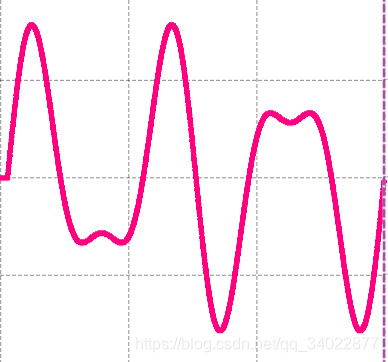
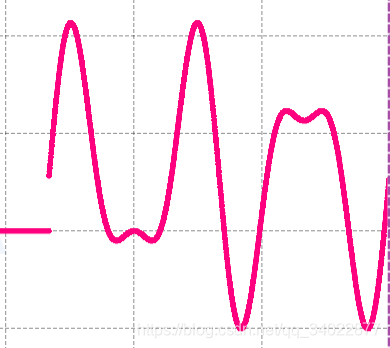
这个是一个幅度为2，频率为3的正弦波，叠加上一个幅度为1，频率为5的谐波而成的信号。

//data{]:用于存放产生的数据
//PI：也就是3.14159...，是DSP库里面设置好的变量，直接用就行
//num：总的数据数量。
for (i = 0; i < num; i++) //生成信号序列
{
    data[i] = 1
        	+2 * arm_sin_f32(2 * PI * 3 * i / num)
    		+1 * arm_sin_f32(2 * PI * 5 * i / num);
}

这里在上面的信号基础上加入了幅度为1的直流偏置。

频率的理解

先说明下，我是电子科学与技术专业，专业并没有教DSP。很多内容都是自己感兴趣，在电赛应用中自己思索出来的，经过实践的验证没有问题。如果有理论上的错误，或者不是那么专业的地方，希望及时指正。

我们现在用下面的代码产生一组数据。

for (i = 0; i < 1024; i++) //生成信号序列
{
    data[i] =  arm_sin_f32(2 * PI * 1 * i / num);
}

这组数据包含1024个点，这1024个点正好描述了一个幅度为1的正弦周期。

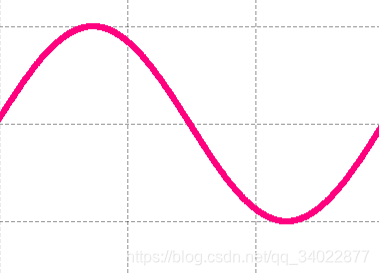
那么问题来了，这个虚拟出来的正弦，频率是多少？

我们可以有下面两种解释方式：

1. 采样率是1024，去采集1hz的信号，采样了1s，也就采样了1024个点。那么我们虚拟的这个正弦波就是1hz。
2. 采样了是10240，去采集10hz的信号，采样了0.1s，也就采样了1024个点，那么我们虚拟的这个正弦波就是10hz。

由此可见这个正弦波是没有真正的频率可言的，跟我们观察的条件有关系，观察的条件不同，频率就不同（好像这个叫做观察的窗）。这个正弦波只有相对频率。

一组数据就是一组数据，需要有具体的应用背景才有含义，我们在虚拟数据时，并没有说这1024个数是采集了多少时间，也就没有赋予他时间上的含义，所以无法知道他一秒有多少给周期。

这里我们可以结合FFT变换时的频率处理，他们的原理是一样的，FFT处理时候我们会把$\frac{采样率}{采样点数}$当作频率分辨率，其他频率是频率分辨率的倍数。

对此，我平时是这样理解的：

如果我们虚拟了1024个点，那么我们就当采样率是1024，采样了1s。

下面就是一个1hz信号和5hz信号的叠加。

for (i = 0; i < 1024; i++) //生成信号序列
{
    data[i] =  arm_sin_f32(2 * PI * 1 * i / num)
    +arm_sin_f32(2 * PI * 5 * i / num);
}

024，采样了1s。

下面就是一个1hz信号和5hz信号的叠加。

for (i = 0; i < 1024; i++) //生成信号序列
{
    data[i] =  arm_sin_f32(2 * PI * 1 * i / num)
    +arm_sin_f32(2 * PI * 5 * i / num);
}

未若头发因风起

• 注重分享学习的精神，此资源0积分下载（资源审核通过后更新

• 本文章是DSP系列中的一篇。目录为：（暂时还没写

• 如果觉得本文章对你有帮助，就请大方地点个赞吧。