文章目录
Introduction
1、解决未知故障检测的问题
2、将未知故障添加到故障模式库以自适应更新故障诊断模型
研究对象:配电网设备的故障诊断
方法:粒子群优化-支持矢量数据描述(PSO-SVDD)
Data collecting

Method
支持矢量数据描述(SVDD)
类似于SVM,一分类问题
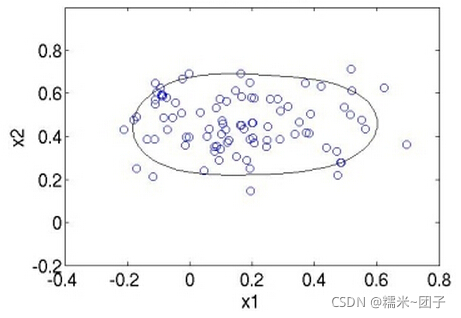
找一个最小的超球面将数据合理全部包裹
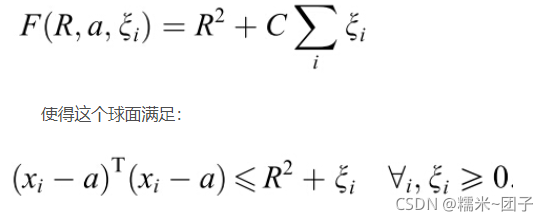
ξ
\xi
ξ为松弛变量,防止模型过拟合
使用拉格朗日乘子法(与SVM一致)

带回拉格朗日函数
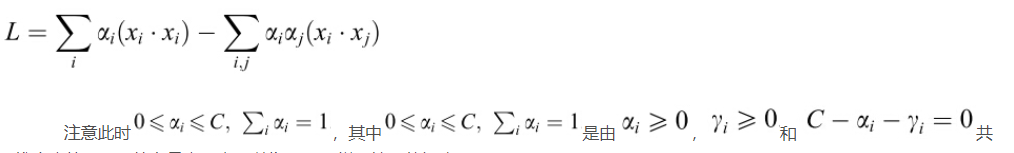
同推出来的。上面的向量内积也可以像SVM那样用核函数解决:
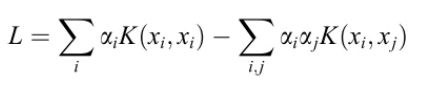
粒子群优化(PSO)
粒子群算法(PSO)属于群智能算法的一种,是通过模拟鸟群捕食行为设计的。假设区域里就只有一块食物(即通常优化问题中所讲的最优解),鸟群的任务是找到这个食物源。鸟群在整个搜寻的过程中,通过相互传递各自的信息,让其他的鸟知道自己的位置,通过这样的协作,来判断自己找到的是不是最优解,同时也将最优解的信息传递给整个鸟群,最终,整个鸟群都能聚集在食物源周围,即我们所说的找到了最优解,即问题收敛。
粒子群算法通过设计一种无质量的粒子来模拟鸟群中的鸟,粒子仅具有两个属性:速度
v
i
v_i
vi? 和位置
x
i
x_i
xi?,速度代表移动的快慢,位置代表移动的方向。每个粒子在搜索空间中单独的搜寻最优解,并将其记为当前个体极值
p
i
p_i
pi?,并将个体极值与整个粒子群里的其他粒子共享,找到最优的那个个体极值作为整个粒子群的当前全局最优解
p
g
p_g
pg?,粒子群中的所有粒子根据自己找到的
p
i
p_i
pi? 和整个粒子群共享的
p
g
p_g
pg? 来调整自己的速度和位置。粒子群算法的思想相对比较简单,主要分为:1、初始化粒子群;2、评价粒子,即计算适应值;3、寻找个体极值;4、寻找全局最优解;5、修改粒子的速度和位置。
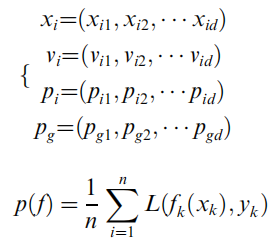
f
k
f_k
fk?是一个由
n
?
1
n-1
n?1个训练样本组成的分类器,
f
k
(
x
k
)
f_k(x_k)
fk?(xk?) 是当前分类器结果,
y
k
y_k
yk?是标签。如果分类准确,
L
(
.
)
=
1
L(.)=1
L(.)=1,否则,
L
(
.
)
=
0
L(.)=0
L(.)=0。
根据
p
g
p_g
pg? 和
p
i
p_i
pi? 来优化当前参数
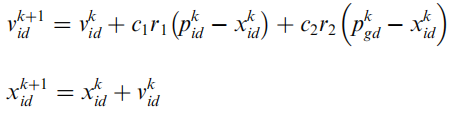
c
1
,
c
2
c_1,c_2
c1?,c2?是加速度因子,一般
c
1
=
c
2
c_1=c_2
c1?=c2? ~[0,4],
r
1
,
r
2
r_1,r_2
r1?,r2? 以[0,1]随机分布,
k
k
k 是当前迭代次数。
加入惯性因子
ω
\omega
ω,确定粒子在迭代前继承速度的程度,以获得粒子的平衡探索能力:
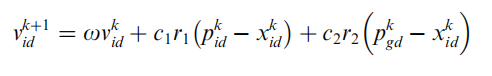
ω
\omega
ω 越大,PSO收敛速度越快,但很难得到准确的解决方案;
ω
\omega
ω 越小,PSO收敛速度越慢,就越容易进入局部最优值。对于
ω
\omega
ω ,一般采用推荐的线性递减惯性加权策略来平衡全局搜索和局部搜索的性能。
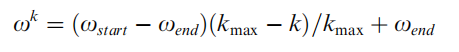
在公式中,
ω
s
t
a
r
t
\omega_{start}
ωstart?是初始惯性权重,
ω
e
n
d
\omega_{end}
ωend?是最大迭代次数时的惯性权重,
ω
m
a
x
\omega_{max}
ωmax?是最大迭代次数。
未知故障识别过程
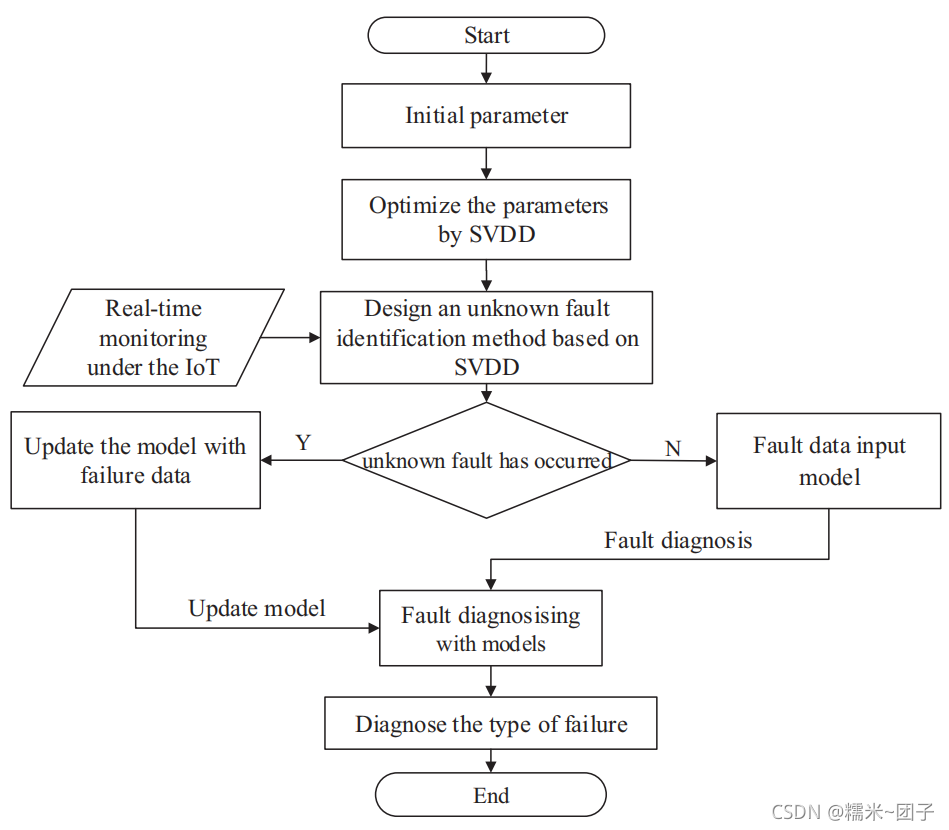
PSO-SVDD算法流程
Experiment and Results
数据采集选择
简单来说,24个传感器( X 1 ? 24 X_{1-24} X1?24?),34组数据( Y 1 ? 34 Y_{1-34} Y1?34?),7类故障( D 1 ? 7 D_{1-7} D1?7?)。前30组数据为已知故障训练集,后4组数据为未知故障测试集。
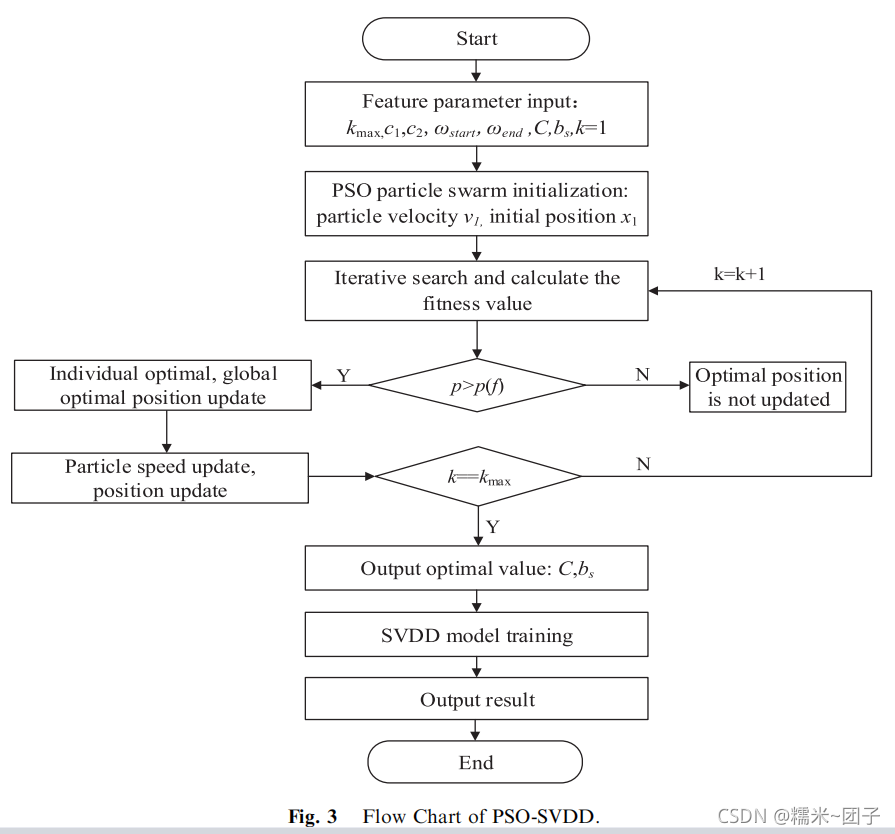
PSO-SVDD算法和模型验证
计算SVDD算法中惩罚参数
C
C
C 和核参数
b
f
b_f
bf? 的适应度参数

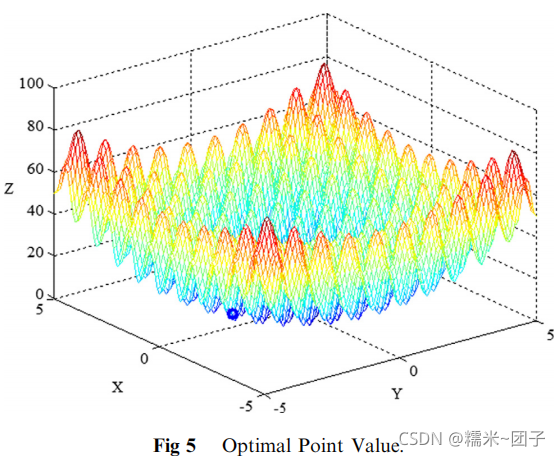
由图4,最佳适应度为80.6,取最优参点值,如图5,得到的最优参数组合结果为
C
=
0.05
,
b
f
=
8
C=0.05,b_f=8
C=0.05,bf?=8
根据训练故障数据与特征参数的对应关系,可以知道,在SVDD模型下,训练数据的每个特征参数分布在[-4,4]之间的范围内,离散结果如图7所示。

测试结果:
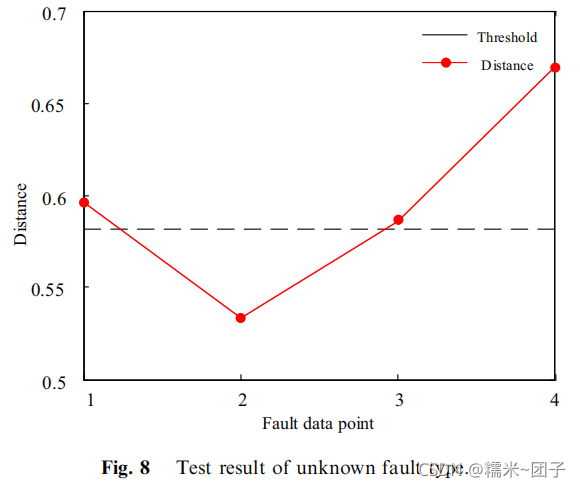
文中说是四组数据都超过了阈值,成为4类未知故障(存疑:这不是有一类是在阈值以下吗?)