[嵌入式]芯动力——硬件加速设计方法 学习笔记 7.静态时序分析1

静态时序分析

为何要进行静态时序分析？

在综合阶段，我们需要已经进行了时序约束，也会产生一个时序分析的报告，但是当时也提到，由于我们没有生成时钟树，也没有进行布局布线的操作，所以这个时序分析的结果是不精确的，所以在我们的后端的各个其他环节中，均需要进行静态时序分析来判断时序是否满足约束。

那么静态时序分析的特点是什么呢？主要有以下几点：

1. 速度快。静态时序分析仅仅针对寄存器，检查寄存器的翻转时间满足时序约束的要求即可，不需要看到每个寄存器的行为和波形，所以速度很快。
2. 不需要测试向量。不用进行仿真。
3. 只针对同步电路。异步电路由于没有时钟和寄存器，无法进行静态时序分析。

所以，其实静态时序分析理论上也是一种仿真的手段，只是他检查的功能点很特殊。所以如果动态的仿真（包括前仿和后仿）已经非常理想的覆盖了所有的应用场景和功能点，我们是可以不用进行静态时序分析的。但是这种情况非常理想，基本在实际中不会出现。

静态时序分析的基本概念

Setup Time

时钟上升沿之前数据必须保持稳定的时间

Hold Time

时钟上升沿之后数据依然保持稳定的时间

Time Slack

主要用来表示实际数据到达时间和setup time与hold time之间的差，裕量大于0就说明满足时序约束，数据能够被正确采样。

静态时序分析的四种路径

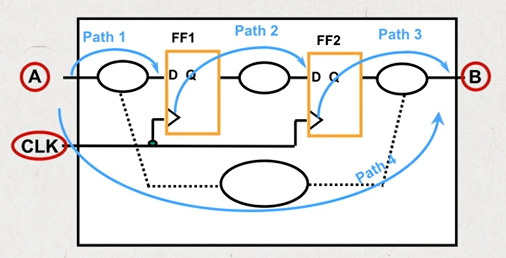
path1：输入到寄存器

path2：寄存器到寄存器

path3：寄存器到输出

path4：输入到输出

reg2reg的建立时间的检查

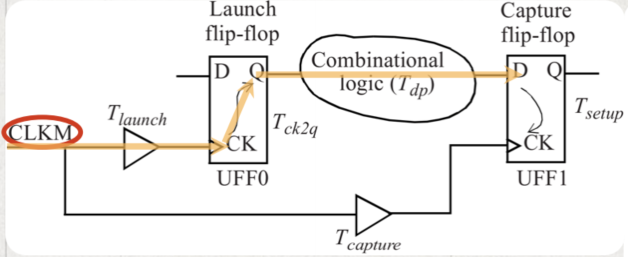
上面是一个典型的寄存器到寄存器的时序模型。$T_{launch}$一般称为发射时间，是指时钟到第一个寄存器的延时，$T_{capture}$称为捕获时间，是指时钟到第二个寄存器的延时，他们之间的差值，一般称为$T_{skew}$。$T_{ck2q}$是指第一个寄存器的CK到Q端的延时，$T_{dp}$是两个寄存器之间的组合逻辑的延时，$T_{setup}$就是指建立时间。

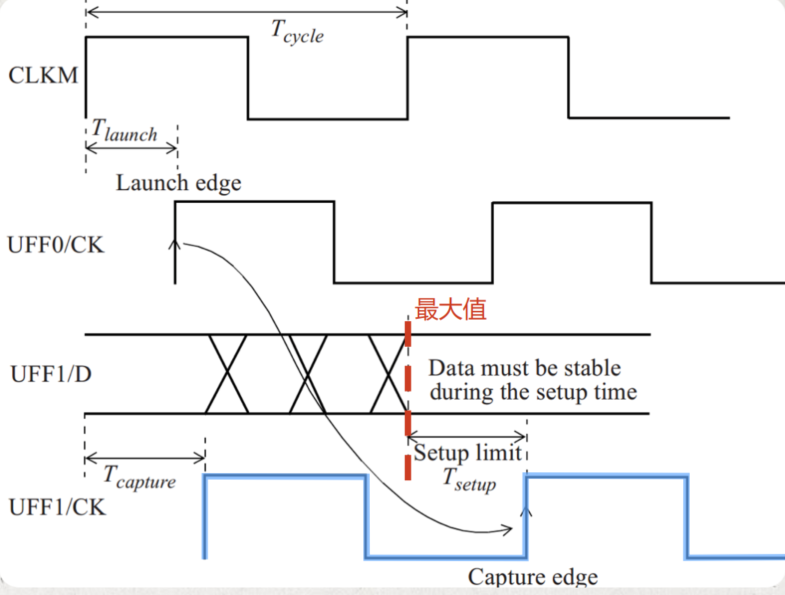
那么，由上面这幅图就可以分析得出，寄存器到寄存器间的建立时间需要满足的公式：
$$T_{launch}+T_{ck2q}+T_{dp}<T_{capture}+T_{cycle}?T_{setup}$$
左边的部分，就是第一个寄存器的延时总和，右边的部分前两项是数据被第二个寄存器捕获的延时值。

下面我们来看一个真实的时序分析的报告：

这幅图对应发射路径，可以看到，时序检查的起点是UFF0，终点是UFF1，路径归属的时钟组为CLKM，一般来说，工具将时序检查的终点的时钟作为路径归属时钟组。

Path Type这一项标记为max，这是说在setup time检查中，由于可变的项基本只有$T_{dp}$，也就是两个寄存器之间的组合逻辑延时，所以，在所有器件延时最大时，setup time仍然能够满足，就说明时间裕量是足够的。

反过来说，Path Type为max就是对setup time进行检查，为min就是对hold time进行检查。

下面这张图可以看到最终的slack是9.41，是大于0的，所以这个时序是满足要求的，从这个时序报告中，我们也能找到我们上面公式所讲的所有延时值。第一幅图，就对应公式的左边，称为data arrival time，第二幅图，对应公式的右边，称为data required time，这两个值相减大于0，就说明建立时间满足时序要求。

arrival time，第二幅图，对应公式的右边，称为data required time，这两个值相减大于0，就说明建立时间满足时序要求。