答应了汤老板快一个月的推文,这次没有下次一定了(手动狗头
抛砖引玉部分,在谈控制思路以前,先谈谈执行器件——电机
不光是智能车,其实我本科接触过的控制系统90%的最直接的执行器件就是电机(包括直流减速电机、无刷电机、舵机、步进电机等等等等),而电机是一个惯性系统,既给定与响应之间的关系如下:
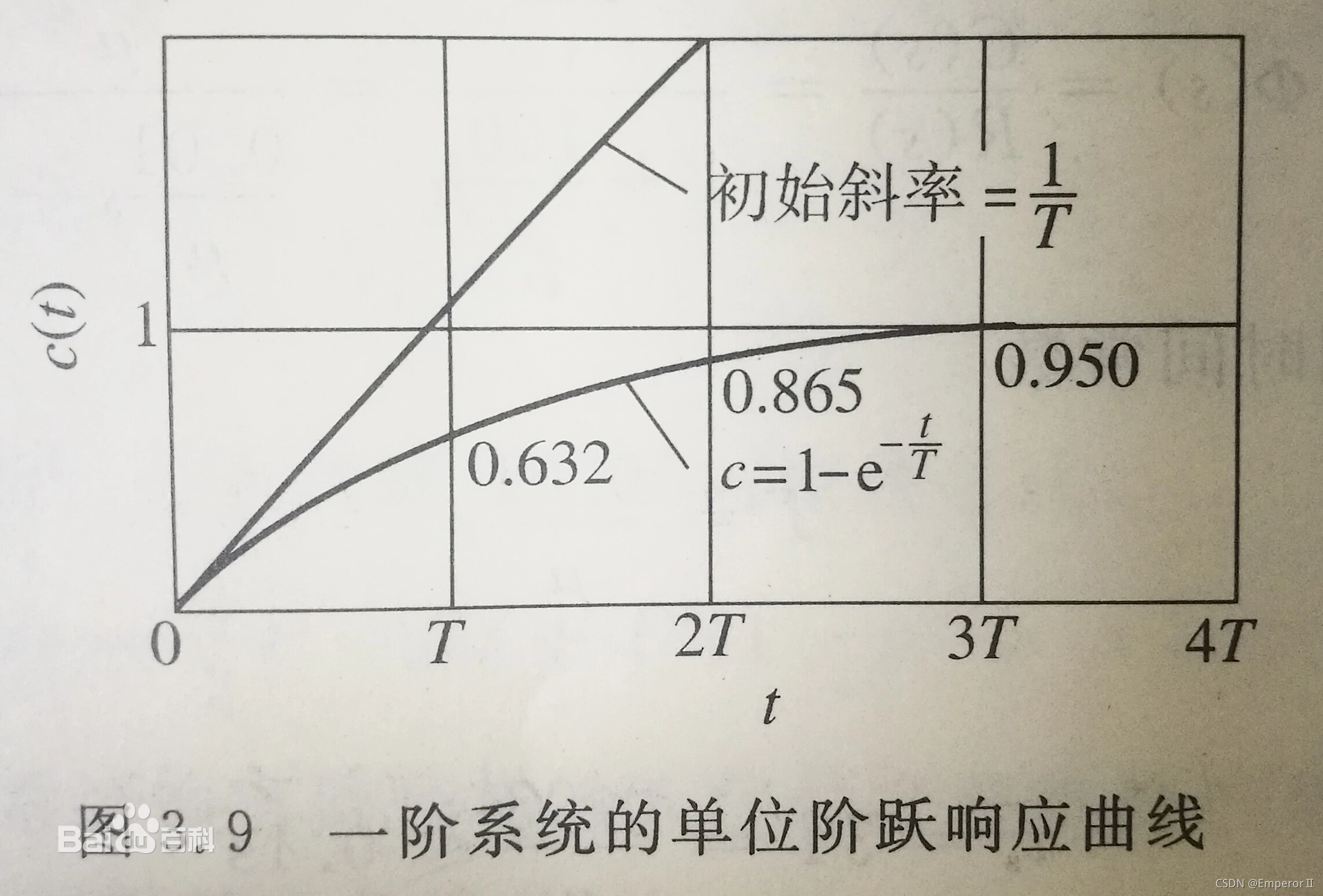
由于本人水平有限,借用百度百科对惯性环节的介绍惯性环节的输出一开始并不与输入同步按比例变化,直到过渡过程结束,y(t)才能与x(t)保持比例。这就是惯性的反映。
简而言之:惯性环节的特点反映在控制效果上就是两个字“滞后”
如何应对
那么,如何应对这个环节的滞后呢
1.最简单的方法当然是加大P或者增加微分项D。但是,单纯的加大P会导致超调量的增加,而微分量D,一方面过大会导致系统震荡,另一方面,引用韩京清教授在“自抗扰控制技术”一文中的话来说:

2.通过模糊算法,ADRC算法等复杂的算法来达到较好的控制策略,如果有能力调好这些算法且处理器能够支持这些算法的运行当然是可以这么做的,但是这类算法要么就因为其本身的非线性特征导致很难找到调试规律(模糊PID),要么加入了一些对反馈的特殊处理而导致很依赖处理器的运算能力(ADRC),尤其是当前阶段裸片STM32F407系列单片机能达到200RMB的天价情况下,不建议在处理器上烧钱。
3.既然系统本身是滞后的,那么为什么不直接控制系统的超前(微分)量呢?这就引出了直立车当前最主流的控制策略:串级PID控制。
在说直立车的串级PID控制之前,先从电机的串级PID控制谈起,也就是自控书和电机拖动控制书上出现的电流环控制谈起,对于电机转速控制来说,转速为最终控制量,而电机电流与电机扭矩T成正相关,因此电机的电流可以近似看为电机转速n的微分量乘以一个比例,既:n=k*di/dt。
这里找不到电机单环控制和双环控制的效果对比图了,但是我记得在电气大三专业课电机拖动与控制技术中有单环控制和双环控制的波形图对比,不管是响应速度和超调量双环控制对比单环控制还是有很大提升的。
如何制定控制策略
其实仔细看完上述三种控制策略的对比,应该已经知道想要达到一个快准稳控制效果的思路是什么了,那就是通过获取超前量来弥补系统本身执行器件的滞后,对于智能车来说,对应到直立环和转向环,那就采用串级PID来控制车模的转向加速度(当然四轮的舵机转向环由于舵机的存在导致控制频率不可能大于100Hz就不要用了,前几天某廖姓学弟据然用2ms的输出频率控制10ms的执行周期得执行器件。。。),对应到赛道信息采集上,则尽可能超前的采集赛道信息,包括但不局限于加长摄像头高度和电感前瞻,当然采集的信息太超前也不好,会导致只看前面的而不顾车模轮子所在的赛道容易轧路肩。
在制定了一个合理的控制策略后,其实每个环基本上单P比例调节就能达到很理想的控制效果了(在结构合理的情况下,调个2.7m/s进个国赛是可以的),至于如何继续提速就需要合理的调整参数和控制策略,多花点时间打磨算法了。
看完上面的分析,其实就可以理解为什么串级PID的意义了,也就是各届直立车报告中的经典控制框图(下面引用自己的报告):
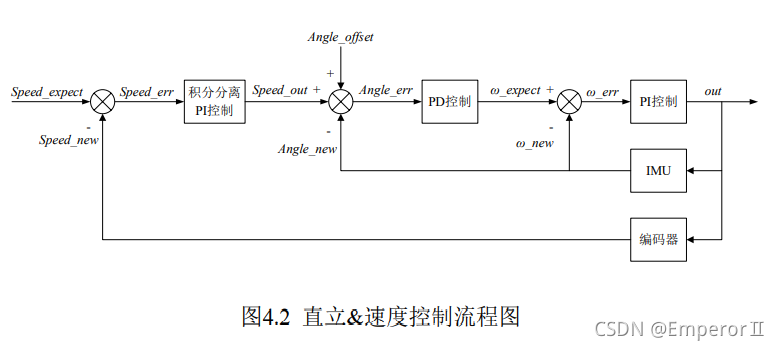
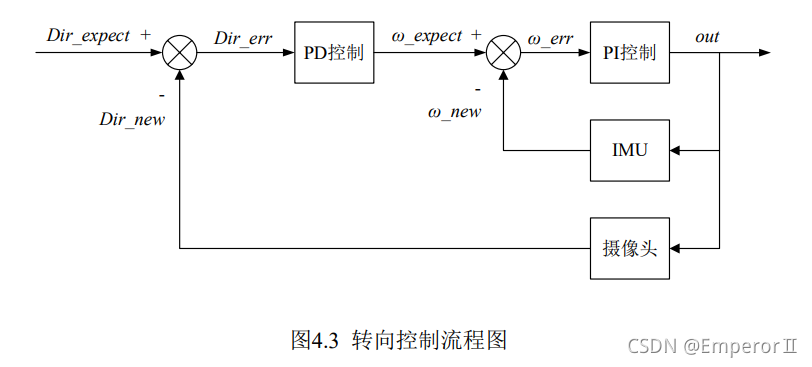
另外在这多提一句,由于速度环和直立环是串在一起的,为了较快的达到期望速度,直立环的D项不要使用角加速度项,采用err(t)-err(t-1)才能是直立环D项与速度环输出耦合起来。
直立车的灵魂——姿态解算
别看我上面巴拉巴拉了一大推,但其实控制并不是直立车中最大的一个坑,在制定了合理的策略的情况下,应该很快就能调到较高的速度。
直立车(包括今年的单车,以后的独轮车)最难的部分其实是最最底层的姿态解算,由于不能使用直接输出角度的传感器,只能自己解算角度,而当车模达到一定速度的时候,由于加速度计的干扰和陀螺仪的漂移,互补滤波和卡尔曼滤波结算出来的角度和真实角度之间的偏差可能超乎你的想像,包括做电赛时市面上低于200块钱的姿态解算传感器,在给予较大干扰的情况下,动态偏差能达到10°甚至30°往上的偏差。
对于这种问题,我们今年也只能做到在2.8m/s左右的速度下,跑一圈角度的动态偏差控制在2°以内,由于速度越快,转换所需要的力越大,因此加速度计收到的干扰越大,所以具体做法为:
1.减小加速度计的信任比重
2.互补滤波和二维卡尔曼滤波的信息其实只有三轴信息(y轴角加速度,x轴和z轴的加速度),丢失了另外3轴信息,因此采用同为互补滤波原理的四元数解算。
3.通过观察解算波形发现,在四元数加速度计补偿角速度时,当积分项I的较大时,静态受干扰振荡会很大,当积分项I较小时,动态跟随效果又较差,改进方法是可以将积分项进行一阶低通滤波,改进后能同时获得较好的动、静态效果。