博主刚好进入研二,研究的方向刚好涉及到数字滤波这一块,因此花了一周时间钻研了下数字滤波的实现。
由于本科是电气专业,所以没有数字信号处理相关知识,在一开始看数字信号处理相关理论的时候就显得比较力不从心,尤其是难懂的数学公式。相比看到这里的读者多多少少也有类似的体会。
好在功夫不负有心人,本博主从繁琐的公式中,加上其他博主的博客讲解,领悟了如何使用C代码实现几种经典数字滤波器,可以使其在VS或者单片机上运行而不受限于在matlab上跑仿真。
当然在本篇博客中,主要是以巴特沃斯滤波器做讲解,其他经典滤波器由于数学公式和讲解都比较少,因此没研究出来。若有读者发现较好的资源,欢迎留言一起分享。
好的,读到这里,先讲解一个同学进场会遇到却不是太理解的概念——滤波器的阶数代表什么意思?其实博主一开始也不理解,后来用C代码实现的时候突然顿悟的。答案是:阶数N,代表着在该滤波器中,需要前N个时刻的采样点数据参与运算。
读到这里可能有的读者还不是太理解。没关系,当你读完整篇博客之后,再回过头都这句话试一下。(其实是博主整理了半天语言也没想到一句通俗易懂的话来描述,如果想到了后期再回来更新吧)
一阶滤波器
一阶滤波器呢,是使用数字滤波器来模拟硬件RC滤波器,以抑制干扰信号。一阶低通数字滤波器公式如下:

其中:

好,看到这里,我们可以看到整个公式中,唯一的需要读者自己计算的就是常数q,有了q值,整个数学公式,相比读者就可以使用C语言实现。那么常数q是如何根据我们所需的截止频率和采样间隔求出的呢?请看如下公式:

其中:

到这里,我们可以得到时间常数q的计算公式为:

下面举个例子教大家如何计算。
例如需要一个20Hz的低通滤波器,对信号的采样率为1000Hz(即0.001秒采样一次),因此q的值为206.280.001=0.125。将q值带入到数学公式中,以C语言实现即可。
高阶滤波器
讲解完了一阶滤波器,下面我们来看下高阶滤波器的实现。
看到这里,有读者可能会问,这个阶数怎么选,是选择使用一阶滤波器还是高阶的,高阶滤波器究竟选择几阶?这其实是有一个数学公式计算你所需的滤波器阶数的,但是由于太过繁琐,不好记,因此在工程领域中不推荐记忆。
这里给大家一个经验,就是滤波器阶数越高,滤波效果越好。
因此,若读者的处理器性能足够强,直接上高阶滤波器即可(阶数越高,计算量越大),一般四到六阶即可解决大部分问题。(有的场景需要高阶滤波器才会完全滤除杂波,但是受到处理器性能影响滤除不干净,因此可以适当降低阶数,因此使用公式计算所需阶数基本没有意义,处理器性能达不到,只能降阶层,因此自己用代码测一下波形比通过公式计算简单得多)
下面是IIR滤波器的差分方程(直接型)。

其中:

看到这里,可能有的读者已经觉得公式有点繁琐。不过没有关系,我们继续往下看,代码实现后在会过来品味一下这个公式。
下面是通过matlab工具计算两个系数。
首先在matlab命令行中输入 fdatool或者filterDesigner,回车执行后会弹出一个框,如下图所示。
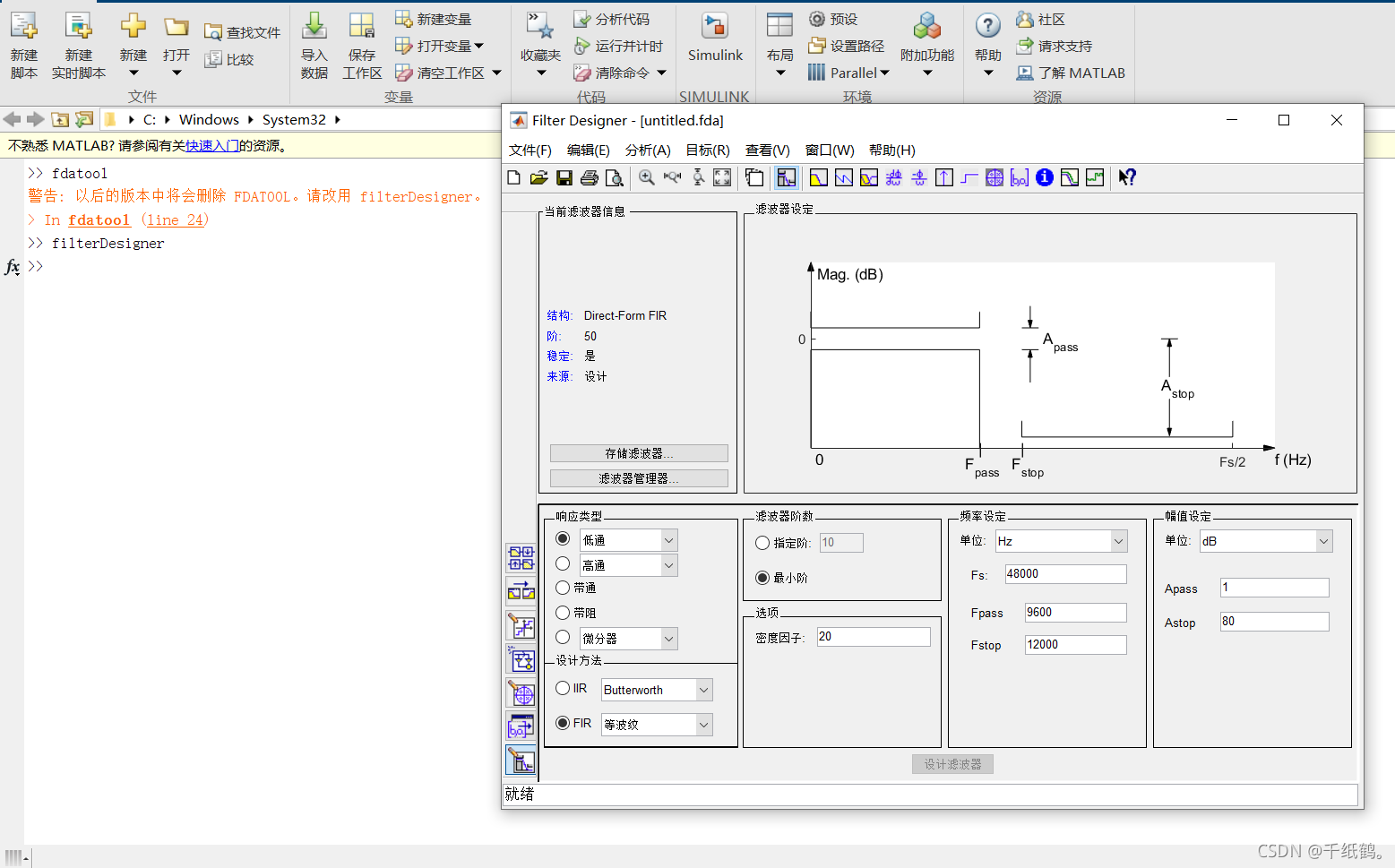
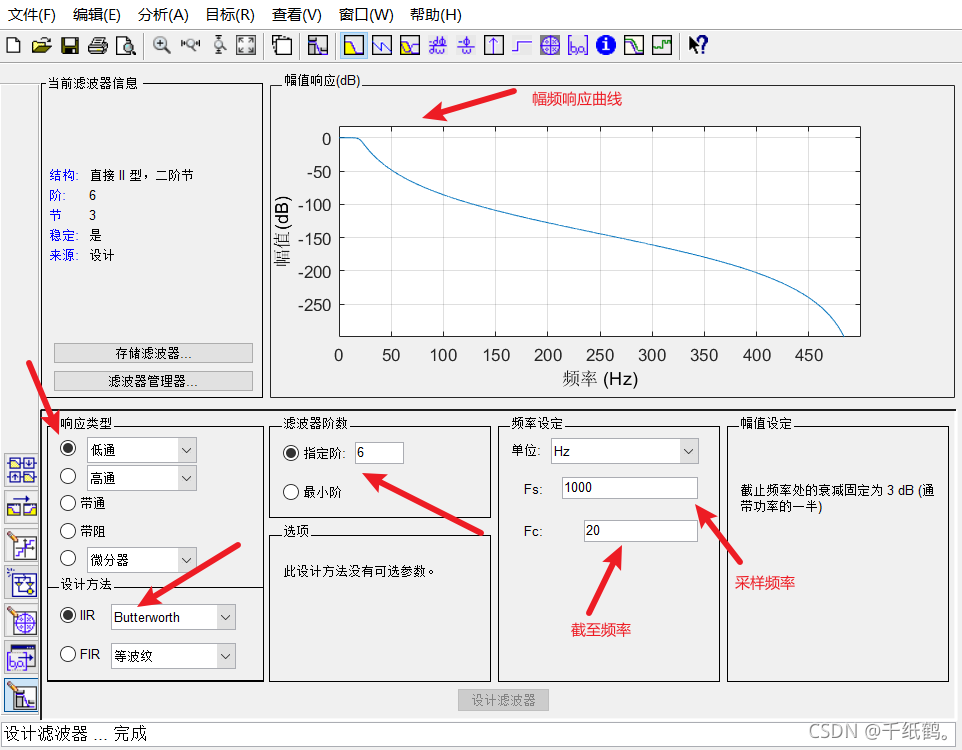
根据业务需求,选择低通或者高通滤波器(注:低通、高通、带通滤波器均为同一个公式,系数不同而已),并设计阶数,输入采样频率和截至频率,点击设计滤波器。
观察幅频响应曲线可以看到,从20Hz开始衰减,50Hz是衰减达到50dB,此处需读者根据自己使用情况调节截止频率的参数。
如下图所示,点击两个按钮,将滤波器系数转换为单节结构,得到滤波器系数。分母为y(n)的系数ak,分子为x(n)系数bk。
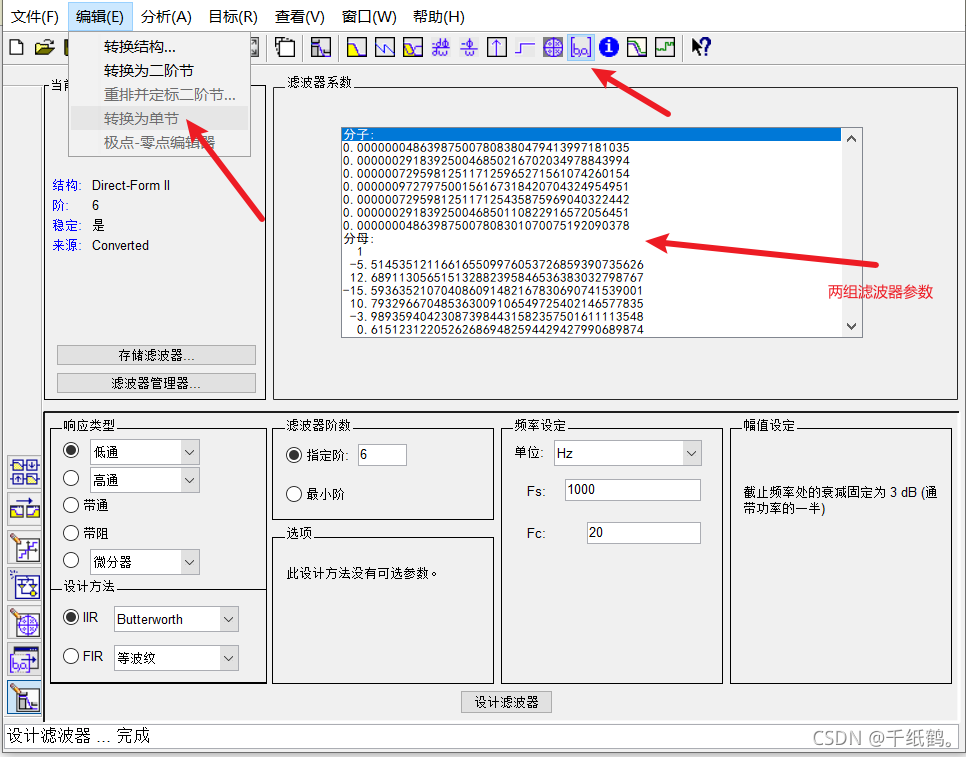
将两组参数带入,得到下面公式。

那本文中,列举了低通滤波器的实现方法,高通滤波器和带通滤波器的实现方法同上,更改系数即可实现。
下面是代码展示:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using 肌电可视化界面.ViewModel;
using NWaves;
using NWaves.Signals;
using NWaves.Filters;
using NWaves.Filters.Bessel;
namespace 肌电可视化界面
{
class SingleProcess
{
int FilterDataNum_VAR = 10000; //全局变量--采集信号的长度
int FilterDataFrequence_VAR = 10000; //全局变量--采集信号的频率
int LowPassCutoffFre_VAR = 150; //全局变量--信号预处理低通截至频率
public Tuple<double[],double[]> Pretreatment()
{
double FilterSamplingInterval = 1.0 / Convert.ToDouble( FilterDataFrequence_VAR); //全局变量--采集信号的间隔
double[] Sin200Hz=new double[FilterDataNum_VAR],Sin300Hz = new double[FilterDataNum_VAR], Sin1Hz = new double[FilterDataNum_VAR], Sin50Hz = new double[FilterDataNum_VAR], Sin100Hz = new double[FilterDataNum_VAR];
double[] InputData = new double[FilterDataNum_VAR];
int x = 0;
for (double i = 0;x< FilterDataNum_VAR; i=i+ FilterSamplingInterval,x++)
{
//Sin200Hz[x] = Math.Sin(Math.PI * 400 * i);
Sin300Hz[x] = Math.Sin(Math.PI * 600 * i);
//Sin1Hz[x] = Math.Sin(Math.PI * 2.0 * i);
Sin50Hz[x] = Math.Sin(Math.PI * 100 * i);
//Sin100Hz[x] = Math.Sin(Math.PI * 200 * i);
InputData[x] = Sin200Hz[x] + Sin300Hz[x] + Sin1Hz[x]+ Sin50Hz[x]+ Sin100Hz[x];
}
//var OutputData=FirstOrderLowPass(InputData);
//var OutputData = IIRLowPassFilter(InputData);
//var OutputData = IIRNotchFilter(InputData);
//var OutputData = IIRLowPassFilter_5(InputData);
var OutputData = IIRLowPassFilter_6(InputData);
//var OutputData = IIRBandPassFilter_6(InputData);
//OutputData = IIRHighPassFilter_3(OutputData);
//OutputData = IIRNotchFilter(OutputData);
//OutputData = IIRLowPassFilter(OutputData);
//var OutputData = FourthOrderRCLowpassFilter(InputData);
Tuple<double[], double[]> value = new Tuple<double[], double[]>(InputData, OutputData);
return value;
}
public double[] FirstOrderLowPass(double[] ProSingle) //一阶低通滤波
{
double[] FilteredData =new double[FilterDataNum_VAR]; //滤波后数据
double LowPassCoefficient = (1.0 / FilterDataFrequence_VAR) * 2 * 3.1415926 * LowPassCutoffFre_VAR; //低通滤波器系数
FilteredData[0] = ProSingle[0];
for(int i=1;i< FilterDataNum_VAR;i++)
{
FilteredData[i] =LowPassCoefficient * ProSingle[i] + ((1.0 - LowPassCoefficient) * FilteredData[i - 1]);
}
return FilteredData;
}
public double[] IIRLowPassFilter(double[] ProSingle) //IIR3阶低通滤波
{
double[] FilteredData = new double[FilterDataNum_VAR]; //滤波后数据
FilteredData[0] = ProSingle[0];
FilteredData[1] = ProSingle[1];
FilteredData[2] = ProSingle[2];
FilteredData[3] = ProSingle[3];
for (int i = 3; i < FilterDataNum_VAR; i++)
{
FilteredData[i] = 0.00009544*ProSingle[i] + 0.0002863 * ProSingle[i - 1] + 0.0002863*ProSingle[i - 2] + 0.00009844 * ProSingle[i - 3] - (-2.81157) * FilteredData[i - 1] - 2.64048 * FilteredData[i - 2] - (-0.828146) * FilteredData[i - 3];
}
return FilteredData;
}
public double[] IIRNotchFilter(double[] ProSingle) //IIR陷波
{
double[] FilteredData = new double[FilterDataNum_VAR]; //滤波后数据
double[] W = new double[3];
double[] IIR_B = new[] { 0.9984039, -1.995822607, 0.998403955 };
double[] IIR_A =new []{1, -1.995822607, 0.9968079114};
W[0] = 0; W[1] = 0; W[2] = 0;
for (int i = 0;i< FilterDataNum_VAR;i++)
{
W[0] = ProSingle[i] - IIR_A [1]* W[1] - IIR_A [2]* W[2];
FilteredData[i] = IIR_B[0] * W[0] + IIR_B[1] * W[1] + IIR_B[2] * W[2];
W[2] = W[1];
W[1] = W[0];
}
return FilteredData;
}
public double[] IIRLowPassFilter_5(double[] ProSingle) //IIR5阶低通滤波
{
double[] FilteredData = new double[FilterDataNum_VAR]; //滤波后数据
FilteredData[0] = ProSingle[0];
FilteredData[1] = ProSingle[1];
FilteredData[2] = ProSingle[2];
FilteredData[3] = ProSingle[3];
FilteredData[4] = ProSingle[4];
FilteredData[5] = ProSingle[5];
for (int i = 5; i < FilterDataNum_VAR; i++)
{
FilteredData[i] = 0.000000200242067359682832116980072401091 * ProSingle[i]
+ 0.000001001210336798414160584900362005456 * ProSingle[i - 1]
+ 0.000002002420673596828321169800724010912 * ProSingle[i - 2]
+ 0.000002002420673596828321169800724010912 * ProSingle[i - 3]
+ 0.000001001210336798414160584900362005456 * ProSingle[i - 4]
+ 0.000000200242067359682832116980072401091 * ProSingle[i - 5]
- (-4.695040626100188241309751902008429169655) * FilteredData[i - 1]
- 8.82614592256382479718013200908899307251 * FilteredData[i - 2]
- (-8.30396669308456125691009219735860824585) * FilteredData[i - 3]
- 3.909893994115305027037265972467139363289 * FilteredData[i - 4]
- (-0.737026189748224092035400190070504322648) * FilteredData[i - 5];
}
return FilteredData;
}
public double[] IIRLowPassFilter_6(double[] ProSingle) //IIR6阶低通滤波
{
double[] FilteredData = new double[FilterDataNum_VAR]; //滤波后数据
FilteredData[0] = ProSingle[0];
FilteredData[1] = ProSingle[1];
FilteredData[2] = ProSingle[2];
FilteredData[3] = ProSingle[3];
FilteredData[4] = ProSingle[4];
FilteredData[5] = ProSingle[5];
FilteredData[6] = ProSingle[6];
for (int i = 6; i < FilterDataNum_VAR; i++)
{
FilteredData[i] = 0.000000009167825068393774824625978674131 * ProSingle[i]
+ 0.000000055006950410362648947755872044785 * ProSingle[i - 1]
+ 0.000000137517376025906622369389680111962 * ProSingle[i - 2]
+ 0.000000183356501367875496492519573482616 * ProSingle[i - 3]
+ 0.000000137517376025906622369389680111962 * ProSingle[i - 4]
+ 0.000000055006950410362648947755872044785 * ProSingle[i - 5]
+ 0.000000009167825068393774824625978674131 * ProSingle[i - 6]
- (-5.635880915490254494670807616785168647766) * FilteredData[i - 1]
- 13.245104571761700640308845322579145431519 * FilteredData[i - 2]
- (-16.614170156135600109337246976792812347412) * FilteredData[i - 3]
- 11.731246791933443773814360611140727996826 * FilteredData[i - 4]
- (-4.420971029104483918104051554109901189804) * FilteredData[i - 5]
- 0.694671323775999050020857339404756203294 * FilteredData[i - 6];
}
return FilteredData;
}
public double[] IIRHighPassFilter_3(double[] ProSingle) //IIR3阶高通滤波
{
double[] FilteredData = new double[FilterDataNum_VAR]; //滤波后数据
FilteredData[0] = ProSingle[0];
FilteredData[1] = ProSingle[1];
FilteredData[2] = ProSingle[2];
FilteredData[3] = ProSingle[3];
for (int i = 3; i < FilterDataNum_VAR; i++)
{
FilteredData[i] = 0.987512174869590753090164980676490813494 * ProSingle[i]
+ -2.962536524608772481315099867060780525208 * ProSingle[i - 1]
+ 2.962536524608772481315099867060780525208 * ProSingle[i - 2]
+ -0.987512174869590753090164980676490813494 * ProSingle[i - 3]
- (-2.974867424113648350925132035627029836178) * FilteredData[i - 1]
- 2.950049679327468421519142793840728700161 * FilteredData[i - 2]
- (-0.975180295515609030232440090912859886885) * FilteredData[i - 3];
}
return FilteredData;
}
public double[] IIRBandPassFilter_6(double[] ProSingle) //IIR6阶带通滤波
{
double[] FilteredData = new double[FilterDataNum_VAR]; //滤波后数据
FilteredData[0] = ProSingle[0];
FilteredData[1] = ProSingle[1];
FilteredData[2] = ProSingle[2];
FilteredData[3] = ProSingle[3];
FilteredData[4] = ProSingle[4];
//FilteredData[5] = ProSingle[5];
//FilteredData[6] = ProSingle[6];
for (int i = 6; i < FilterDataNum_VAR; i++)
{
FilteredData[i] = 0.00157610530654539037105632548474432042 * ProSingle[i]
+ 0 * ProSingle[i - 1]
+ -0.00315221061309078074211265096948864084 * ProSingle[i - 2]
+ 0 * ProSingle[i - 3]
+ 0.00157610530654539037105632548474432042 * ProSingle[i - 4]
//+ 0 * ProSingle[i - 5]
//+ -0.018098933007514465820531057715925271623 * ProSingle[i - 6]
- (-3.882301518552897512392974022077396512032) * FilteredData[i - 1]
- 5.655640987638847150265064556151628494263 * FilteredData[i - 2]
- (-3.664245505992618223700674207066185772419) * FilteredData[i - 3]
- 0.890907362087139609307939736027037724853 * FilteredData[i - 4];
//- (-0.331778114794525014197290602169232442975) * FilteredData[i - 5]
//- 0.278059917634546460707412052215659059584 * FilteredData[i - 6];
}
return FilteredData;
}
}
}
运行效果:
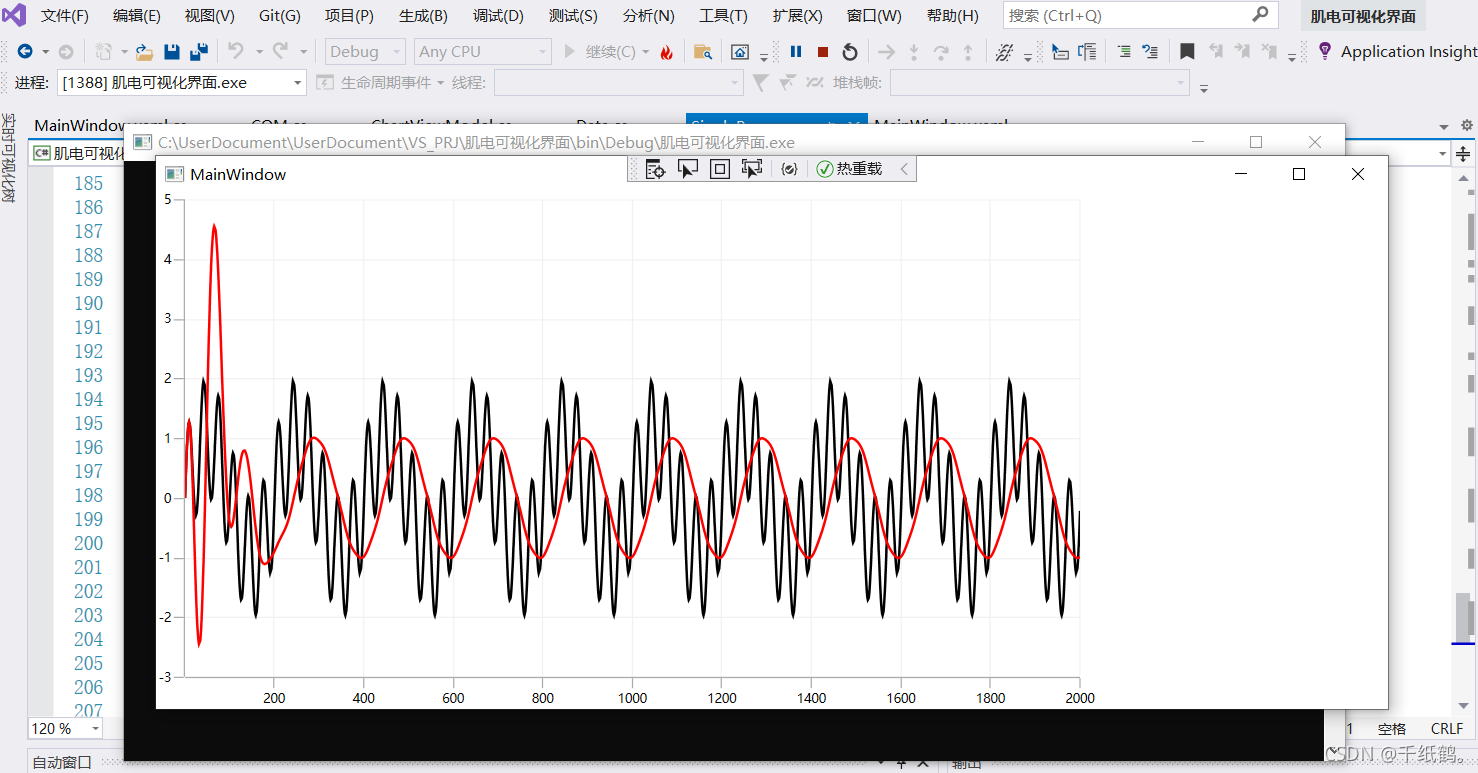
本系统中,仅仅保留了50Hz分量,其他干扰信号全部滤除。(注:本系统需要持续输入信号,不能将短时的采样片段输入,否则会得到如上图前150个采样点的效果,大大影响效果)
喜欢的话,别忘了给博主点个小心心哦。