开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 嵌入式 -> 常见窗函数的C语言实现及其形状，适用于单片机、DSP作FFT运算 -> 正文阅读

[嵌入式]常见窗函数的C语言实现及其形状，适用于单片机、DSP作FFT运算

平台：Windows 10 20H2
Visual Studio 2015
Python 3.8.12 (default, Oct 12 2021, 03:01:40) [MSC v.1916 64 bit (AMD64)] :: Anaconda, Inc. on win32

原作见窗函数的C语言实现 —— Vincent.Cui

可配合C语言实现的FFT与IFFT源代码，不依赖特定平台使用

原代码大量使用了动态内存分配，考虑到部分单片机的限制，我把它们又改回了数组传参的形式。

由于缺少besseli、prod和linSpace函数，有三个窗函数暂时被我用条件编译注释掉了。

源码

WindowFunction.c

/*
*file		WindowFunction.c
*author		Vincent Cui
*e-mail		whcui1987@163.com
*version	0.3
*data		31-Oct-2014
*brief		各种窗函数的C语言实现
*/

#include "WindowFunction.h"
#include <math.h>
#include <stdlib.h>

#if prod_Flag
/*函数名：taylorWin
*说明：计算泰勒窗。泰勒加权函数
*输入：
*输出：
*返回：
*调用：prod()连乘函数
*其它：用过以后，需要手动释放掉*w的内存空间
*        调用示例：ret = taylorWin(99, 4, 40, &w); 注意此处的40是正数 表示-40dB
*/
dspErrorStatus taylorWin(dspUint_16 N, dspUint_16 nbar, dspDouble sll, dspDouble **w)
{
	dspDouble A;
	dspDouble *retDspDouble;
	dspDouble *sf;
	dspDouble *result;
	dspDouble alpha, beta, theta;
	dspUint_16 i, j;

	/*A = R   cosh(PI, A) = R*/
	A = (dspDouble)acosh(pow((dspDouble)10.0, (dspDouble)sll / 20.0)) / PI;
	A = A * A;

	/*开出存放系数的空间*/
	retDspDouble = (dspDouble *)malloc(sizeof(dspDouble) * (nbar - 1));
	if (retDspDouble == NULL)
		return DSP_ERROR;
	sf = retDspDouble;

	/*开出存放系数的空间*/
	retDspDouble = (dspDouble *)malloc(sizeof(dspDouble) * N);
	if (retDspDouble == NULL)
		return DSP_ERROR;
	result = retDspDouble;

	alpha = prod(1, 1, (nbar - 1));
	alpha *= alpha;
	beta = (dspDouble)nbar / sqrt(A + pow((nbar - 0.5), 2));
	for (i = 1; i <= (nbar - 1); i++)
	{
		*(sf + i - 1) = prod(1, 1, (nbar - 1 + i)) * prod(1, 1, (nbar - 1 - i));
		theta = 1;
		for (j = 1; j <= (nbar - 1); j++)
		{
			theta *= 1 - (dspDouble)(i * i) / (beta * beta * (A + (j - 0.5) * (j - 0.5)));
		}
		*(sf + i - 1) = alpha * (dspDouble)theta / (*(sf + i - 1));
	}

	/*奇数阶*/
	if ((N % 2) == 1)
	{
		for (i = 0; i < N; i++)
		{
			alpha = 0;
			for (j = 1; j <= (nbar - 1); j++)
			{
				alpha += (*(sf + j - 1)) * cos(2 * PI * j * (dspDouble)(i - ((N - 1) / 2)) / N);
			}
			*(result + i) = 1 + 2 * alpha;
		}
	}
	/*偶数阶*/
	else
	{
		for (i = 0; i < N; i++)
		{
			alpha = 0;
			for (j = 1; j <= (nbar - 1); j++)
			{
				alpha += (*(sf + j - 1)) * cos(PI * j * (dspDouble)(2 * (i - (N / 2)) + 1) / N);
			}
			*(result + i) = 1 + 2 * alpha;

		}
	}
	*w = result;
	free(sf);

	return DSP_SUCESS;
}
#endif

/*
*函数名：triangularWin
*说明：计算三角窗函数
*输入：
*输出：
*返回：
*调用：
*调用示例：ret = triangularWin(99, w);
*/
dspErrorStatus triangularWin(uint16_t N, double w[])
{
	uint16_t i;

	/*阶数为奇*/
	if ((N % 2) == 1)
	{
		for (i = 0; i < ((N - 1) / 2); i++)
		{
			w[i] = 2 * (double)(i + 1) / (N + 1);
		}
		for (i = ((N - 1) / 2); i < N; i++)
		{
			w[i] = 2 * (double)(N - i) / (N + 1);
		}
	}
	/*阶数为偶*/
	else
	{
		for (i = 0; i < (N / 2); i++)
		{
			w[i] = (i + i + 1) * (double)1 / N;
		}
		for (i = (N / 2); i < N; i++)
		{
			w[i] = w[N - 1 - i];
		}
	}

	return DSP_SUCESS;
}

#if linSpace_Flag
/*
*函数名：tukeyWin
*说明：计算tukey窗函数
*输入：
*输出：
*返回：linSpace()
*调用：
*其它：用过以后，需要手动释放掉*w的内存空间
*        调用示例：ret = tukeyWin(99, 0.5, &w);
*/
dspErrorStatus tukeyWin(dspUint_16 N, dspDouble r, dspDouble **w)
{
	dspErrorStatus retErrorStatus;
	dspUint_16        index;
	dspDouble        *x, *result, *retPtr;
	dspDouble        alpha;

	retErrorStatus = linSpace(0, 1, N, &x);
	if (retErrorStatus == DSP_ERROR)
		return DSP_ERROR;

	result = (dspDouble *)malloc(N * sizeof(dspDouble));
	if (result == NULL)
		return DSP_ERROR;

	/*r <= 0 就是矩形窗*/
	if (r <= 0)
	{
		retErrorStatus = rectangularWin(N, &retPtr);
		if (retErrorStatus == DSP_ERROR)
			return DSP_ERROR;
		/*将数据拷出来以后，释放调用的窗函数的空间*/
		memcpy(result, retPtr, (N * sizeof(dspDouble)));
		free(retPtr);
	}
	/*r >= 1 就是汉宁窗*/
	else if (r >= 1)
	{
		retErrorStatus = hannWin(N, &retPtr);
		if (retErrorStatus == DSP_ERROR)
			return DSP_ERROR;
		/*将数据拷出来以后，释放调用的窗函数的空间*/
		memcpy(result, retPtr, (N * sizeof(dspDouble)));
		free(retPtr);
	}
	else
	{
		for (index = 0; index < N; index++)
		{
			alpha = *(x + index);
			if (alpha < (r / 2))
			{
				*(result + index) = (dspDouble)(1 + cos(2 * PI * (dspDouble)(alpha - (dspDouble)r / 2) / r)) / 2;
			}
			else if ((alpha >= (r / 2)) && (alpha <(1 - r / 2)))
			{
				*(result + index) = 1;
			}
			else
			{
				*(result + index) = (dspDouble)(1 + cos(2 * PI * (dspDouble)(alpha - 1 + (dspDouble)r / 2) / r)) / 2;
			}

		}
	}

	free(x);

	*w = result;

	return DSP_SUCESS;
}
#endif

/*
*函数名：bartlettWin
*说明：计算bartlettWin窗函数
*输入：
*输出：
*返回：
*调用：
*调用示例：ret = bartlettWin(99, w);
*/
dspErrorStatus bartlettWin(uint16_t N, double w[])
{
	
	uint16_t n;

	for (n = 0; n < (N - 1) / 2; n++)
	{
		w[n] = 2 * (double)n / (N - 1);
	}

	for (n = (N - 1) / 2; n < N; n++)
	{
		w[n] = 2 - 2 * (double)n / ((N - 1));
	}

	return DSP_SUCESS;
}

/*
*函数名：bartLettHannWin
*说明：计算bartLettHannWin窗函数
*输入：
*输出：
*返回：
*调用：
*调用示例：ret = bartLettHannWin(99, w);
*/
dspErrorStatus bartLettHannWin(uint16_t N, double w[])
{
	uint16_t n;

	/*奇*/
	if ((N % 2) == 1)
	{
		for (n = 0; n < N; n++)
		{
			w[n] = 0.62 - 0.48 * fabs(((double)n / (N - 1)) - 0.5) + 0.38 * cos(2 * PI * (((double)n / (N - 1)) - 0.5));
		}
		for (n = 0; n < (N - 1) / 2; n++)
		{
			w[n] = w[N - 1 - n];
		}
	}
	/*偶*/
	else
	{
		for (n = 0; n < N; n++)
		{
			w[n] = 0.62 - 0.48 * fabs(((double)n / (N - 1)) - 0.5) + 0.38 * cos(2 * PI * (((double)n / (N - 1)) - 0.5));
		}
		for (n = 0; n < N / 2; n++)
		{
			w[n] = w[N - 1 - n];
		}
	}

	return DSP_SUCESS;
}

/*
*函数名：blackManWin
*说明：计算blackManWin窗函数
*输入：
*输出：
*返回：
*调用：
*调用示例：ret = blackManWin(99, w);
*/
dspErrorStatus blackManWin(uint16_t N, double w[])
{
	uint16_t n;

	for (n = 0; n < N; n++)
	{
		w[n] = 0.42 - 0.5 * cos(2 * PI * (double)n / (N - 1)) + 0.08 * cos(4 * PI * (double)n / (N - 1));
	}

	return DSP_SUCESS;
}

/*
*函数名：blackManHarrisWin
*说明：计算blackManHarrisWin窗函数
*输入：
*输出：
*返回：
*调用：
*调用示例：ret = blackManHarrisWin(99, w);
*  minimum 4-term Blackman-harris window -- From Matlab
*/
dspErrorStatus blackManHarrisWin(uint16_t N, double w[])
{
	uint16_t n;

	for (n = 0; n < N; n++)
	{
		w[n] = BLACKMANHARRIS_A0 - BLACKMANHARRIS_A1 * cos(2 * PI * (double)n / (N)) + \
			BLACKMANHARRIS_A2 * cos(4 * PI * (double)n / (N)) - \
			BLACKMANHARRIS_A3 * cos(6 * PI * (double)n / (N));
	}

	return DSP_SUCESS;
}

/*
*函数名：bohmanWin
*说明：计算bohmanWin窗函数
*输入：
*输出：
*返回：
*调用：
*调用示例：ret = bohmanWin(99, w);
*/
dspErrorStatus bohmanWin(uint16_t N, double w[])
{
	uint16_t n;
	
	double x;

	for (n = 0; n < N; n++)
	{
		x = -1 + n *  (double)2 / (N - 1);
		/*取绝对值*/
		x = x >= 0 ? x : (x * (-1));
		w[n] = (1 - x) * cos(PI * x) + (double)(1 / PI) * sin(PI * x);
	}

	return DSP_SUCESS;
}

/*
*函数名：chebyshevWin
*说明：计算chebyshevWin窗函数
*输入：
*输出：
*返回：
*调用：
*调用示例：ret = chebyshevWin(99,100, w);
*/
dspErrorStatus chebyshevWin(uint16_t N, double r, double w[])
{
	uint16_t n, index;
	
	double x, alpha, beta, theta, gama;

	/*10^(r/20)*/
	theta = pow((double)10, (double)(fabs(r) / 20));
	beta = pow(cosh(acosh(theta) / (N - 1)), 2);
	alpha = 1 - (double)1 / beta;

	if ((N % 2) == 1)
	{
		/*计算一半的区间*/
		for (n = 1; n < (N + 1) / 2; n++)
		{
			gama = 1;
			for (index = 1; index < n; index++)
			{
				x = index * (double)(N - 1 - 2 * n + index) / ((n - index) * (n + 1 - index));
				gama = gama * alpha * x + 1;
			}
			w[n] = (N - 1) * alpha * gama;
		}

		theta = w[(N - 1) / 2];
		w[0] = 1;

		for (n = 0; n < (N + 1) / 2; n++)
		{
			w[n] = (double)(w[n]) / theta;
		}

		/*填充另一半*/
		for (; n < N; n++)
		{
			w[n] = w[N - n - 1];
		}
	}
	else
	{
		/*计算一半的区间*/
		for (n = 1; n < (N + 1) / 2; n++)
		{
			gama = 1;
			for (index = 1; index < n; index++)
			{
				x = index * (double)(N - 1 - 2 * n + index) / ((n - index) * (n + 1 - index));
				gama = gama * alpha * x + 1;
			}
			w[n] = (N - 1) * alpha * gama;
		}

		theta = w[(N / 2) - 1];
		w[0] = 1;

		for (n = 0; n < (N + 1) / 2; n++)
		{
			w[n] = (double)(w[n]) / theta;
		}

		/*填充另一半*/
		for (; n < N; n++)
		{
			w[n] = w[N - n - 1];
		}
	}

	return DSP_SUCESS;
}

/*
*函数名：flatTopWin
*说明：计算flatTopWin窗函数
*输入：
*输出：
*返回：
*调用：
*调用示例：ret = flatTopWin(99, w);
*/
dspErrorStatus flatTopWin(uint16_t N, double w[])
{
	uint16_t n;

	for (n = 0; n < N; n++)
	{
		w[n] = FLATTOPWIN_A0 - FLATTOPWIN_A1 * cos(2 * PI * (double)n / (N - 1)) + \
			FLATTOPWIN_A2 * cos(4 * PI * (double)n / (N - 1)) - \
			FLATTOPWIN_A3 * cos(6 * PI * (double)n / (N - 1)) + \
			FLATTOPWIN_A4 * cos(8 * PI * (double)n / (N - 1));
	}

	return DSP_SUCESS;
}


/*
*函数名：gaussianWin
*说明：计算gaussianWin窗函数
*输入：
*输出：
*返回：
*调用：
*调用示例：ret = gaussianWin(99,2.5, w);
*/
dspErrorStatus gaussianWin(uint16_t N, double alpha, double w[])
{
	uint16_t n;
	double k, beta, theta;

	for (n = 0; n < N; n++)
	{
		if ((N % 2) == 1)
		{
			k = n - (N - 1) / 2;
			beta = 2 * alpha * (double)k / (N - 1);
		}
		else
		{
			k = n - (N) / 2;
			beta = 2 * alpha * (double)k / (N - 1);
		}

		theta = pow(beta, 2);
		w[n] = exp((-1) * (double)theta / 2);
	}

	return DSP_SUCESS;
}

/*
*函数名：hammingWin
*说明：计算hammingWin窗函数
*输入：
*输出：
*返回：
*调用：
*调用示例：ret = hammingWin(99, w);
*/
dspErrorStatus hammingWin(uint16_t N, double w[])
{
	uint16_t n;

	for (n = 0; n < N; n++)
	{
		w[n] = 0.54 - 0.46 * cos(2 * PI *  (double)n / (N - 1));
	}

	return DSP_SUCESS;
}

/*
*函数名：hannWin
*说明：计算hannWin窗函数
*输入：
*输出：
*返回：
*调用：
*调用示例：ret = hannWin(99, w);
*/
dspErrorStatus hannWin(uint16_t N, double w[])
{
	uint16_t n;

	for (n = 0; n < N; n++)
	{
		w[n] = 0.5 * (1 - cos(2 * PI * (double)n / (N - 1)));
	}

	return DSP_SUCESS;
}

#if besseli_Flag
/*
*函数名：kaiserWin
*说明：计算kaiserWin窗函数
*输入：
*输出：
*返回：
*调用：besseli()第一类修正贝塞尔函数
*其它：用过以后，需要手动释放掉*w的内存空间
*        调用示例：ret = kaiserWin(99, 5, &w);
*/
dspErrorStatus kaiserWin(dspUint_16 N, dspDouble beta, dspDouble **w)
{
	dspUint_16 n;
	dspDouble *ret;
	dspDouble theta;

	ret = (dspDouble *)malloc(N * sizeof(dspDouble));
	if (ret == NULL)
		return DSP_ERROR;

	for (n = 0; n < N; n++)
	{
		theta = beta * sqrt(1 - pow(((2 * (dspDouble)n / (N - 1)) - 1), 2));
		*(ret + n) = (dspDouble)besseli(0, theta, BESSELI_K_LENGTH) / besseli(0, beta, BESSELI_K_LENGTH);
	}

	*w = ret;

	return DSP_SUCESS;
}
#endif

/*
*函数名：nuttalWin
*说明：计算nuttalWin窗函数
*输入：
*输出：
*返回：
*调用：
*调用示例：ret = nuttalWin(99, w);
*/
dspErrorStatus nuttalWin(uint16_t N, double w[])
{
	uint16_t n;

	for (n = 0; n < N; n++)
	{
		w[n] = NUTTALL_A0 - NUTTALL_A1 * cos(2 * PI * (double)n / (N - 1)) + \
			NUTTALL_A2 * cos(4 * PI * (double)n / (N - 1)) - \
			NUTTALL_A3 * cos(6 * PI * (double)n / (N - 1));
	}

	return DSP_SUCESS;
}

/*
*函数名：parzenWin
*说明：计算parzenWin窗函数
*输入：
*输出：
*返回：
*调用：
*调用示例：ret = parzenWin(99, w);
*/
dspErrorStatus parzenWin(uint16_t N, double w[])
{
	uint16_t n;
	
	double alpha, k;

	if ((N % 2) == 1)
	{
		for (n = 0; n < N; n++)
		{
			k = n - (N - 1) / 2;
			alpha = 2 * (double)fabs(k) / N;
			if (fabs(k) <= (N - 1) / 4)
			{
				w[n] = 1 - 6 * pow(alpha, 2) + 6 * pow(alpha, 3);
			}
			else
			{
				w[n] = 2 * pow((1 - alpha), 3);
			}
		}
	}
	else
	{
		for (n = 0; n < N; n++)
		{
			k = n - (N - 1) / 2;
			alpha = 2 * (double)fabs(k) / N;
			if (fabs(k) <= (double)(N - 1) / 4)
			{
				w[n] = 1 - 6 * pow(alpha, 2) + 6 * pow(alpha, 3);
			}
			else
			{
				w[n] = 2 * pow((1 - alpha), 3);
			}

		}
	}

	return DSP_SUCESS;
}

/*
*函数名：rectangularWin
*说明：计算rectangularWin窗函数
*输入：
*输出：
*返回：
*调用：
*调用示例：ret = rectangularWin(99, w);
*/
dspErrorStatus rectangularWin(uint16_t N, double w[])
{
	uint16_t n;

	for (n = 0; n < N; n++)
	{
		w[n] = 1;
	}

	return DSP_SUCESS;
}

WindowFunction.h

/*
*file		WindowFunction.h
*author		Vincent Cui
*e-mail		whcui1987@163.com
*version	0.3
*data		31-Oct-2014
*brief		各种窗函数的C语言实现
*/

#ifndef _WINDOWFUNCTION_H_
#define _WINDOWFUNCTION_H_

#include <stdint.h>

#define besseli_Flag	0	//缺少besseli函数
#define prod_Flag		0	//缺少prod函数
#define linSpace_Flag	0	//缺少linSpace函数

#define BESSELI_K_LENGTH 10

#define FLATTOPWIN_A0  0.215578995
#define FLATTOPWIN_A1  0.41663158
#define FLATTOPWIN_A2  0.277263158
#define FLATTOPWIN_A3  0.083578947
#define FLATTOPWIN_A4  0.006947368

#define NUTTALL_A0   0.3635819
#define NUTTALL_A1   0.4891775
#define NUTTALL_A2   0.1365995
#define NUTTALL_A3   0.0106411

#define BLACKMANHARRIS_A0 0.35875
#define BLACKMANHARRIS_A1 0.48829
#define BLACKMANHARRIS_A2 0.14128
#define BLACKMANHARRIS_A3 0.01168

#define PI 3.14159265358979323846264338327950288419717  //定义圆周率值

typedef enum
{
	DSP_ERROR = 0,
	DSP_SUCESS,
}dspErrorStatus;

dspErrorStatus triangularWin(uint16_t N, double w[]);
dspErrorStatus bartlettWin(uint16_t N, double w[]);
dspErrorStatus bartLettHannWin(uint16_t N, double w[]);
dspErrorStatus blackManWin(uint16_t N, double w[]);
dspErrorStatus blackManHarrisWin(uint16_t N, double w[]);
dspErrorStatus bohmanWin(uint16_t N, double w[]);
dspErrorStatus chebyshevWin(uint16_t N, double r, double w[]);
dspErrorStatus flatTopWin(uint16_t N, double w[]);
dspErrorStatus gaussianWin(uint16_t N, double alpha, double w[]);
dspErrorStatus hammingWin(uint16_t N, double w[]);
dspErrorStatus hannWin(uint16_t N, double w[]);
dspErrorStatus nuttalWin(uint16_t N, double w[]);
dspErrorStatus parzenWin(uint16_t N, double w[]);
dspErrorStatus rectangularWin(uint16_t N, double w[]);

#if besseli_Flag
dspErrorStatus kaiserWin(uint16_t N, double beta, double w[]);
#endif

#if prod_Flag
dspErrorStatus taylorWin(uint16_t N, uint16_t nbar, double sll, double w[]);
#endif

#if linSpace_Flag
dspErrorStatus tukeyWin(uint16_t N, double r, double w[]);
#endif

#endif

使用

FFT_N为存放时域数值的数组大小，一般与所采用的FFT点数一致

	double Window[FFT_N] = {0};
	bartLettHannWin(FFT_N, Window);

调用后Window[]内便存入了窗函数的系数，再将这些系数与存放时域数值的数组元素一一相乘应该就行。

形状

以下均为1024点生成的窗函数形状，数据由VS2015产生，图像由 python3 绘制。

三角窗

dspErrorStatus triangularWin(uint16_t N, double w[]);
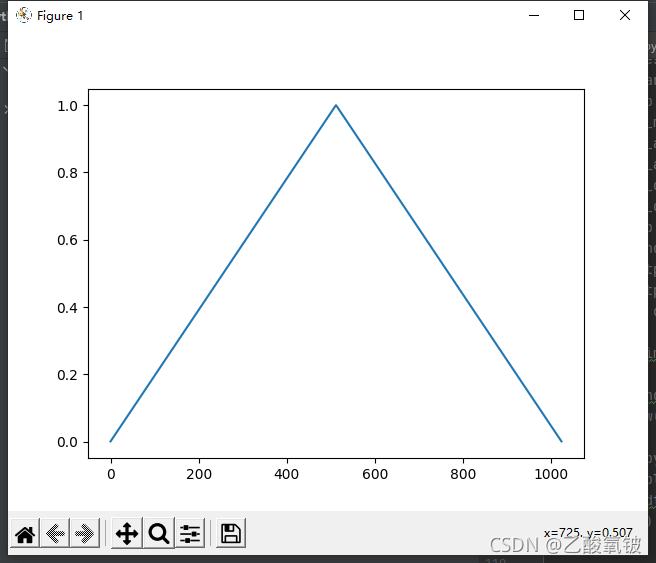
在这里插入图片描述

巴特利特窗

dspErrorStatus bartlettWin(uint16_t N, double w[]);
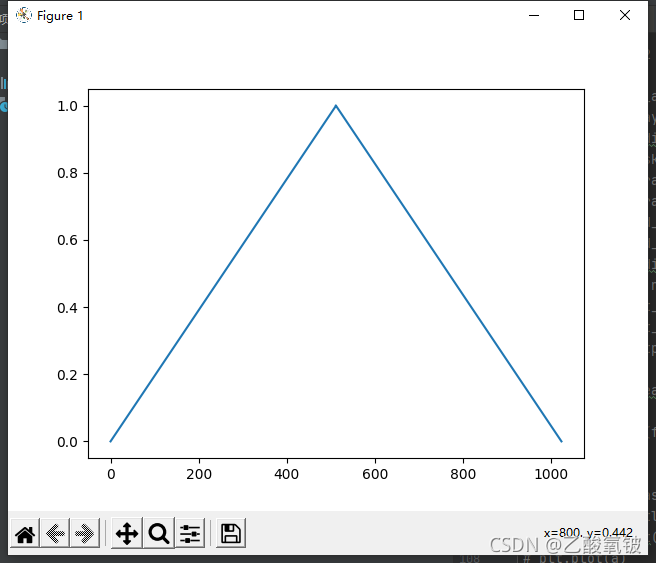
在这里插入图片描述

巴特利特-汉宁窗

dspErrorStatus bartLettHannWin(uint16_t N, double w[]);
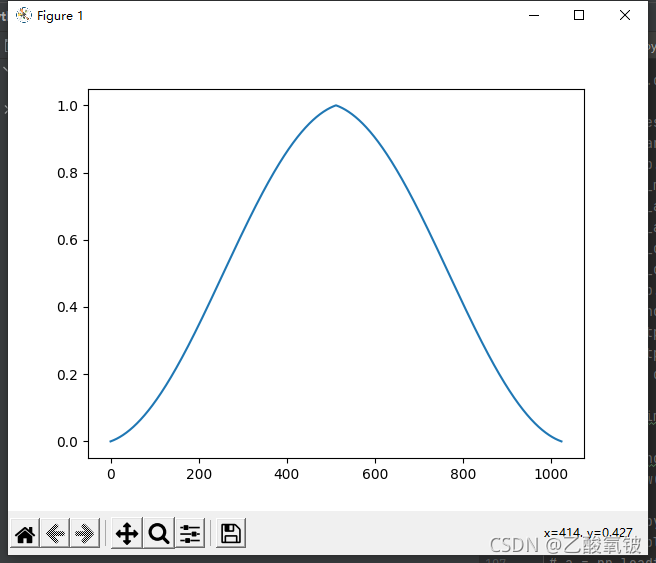
在这里插入图片描述

布莱克曼窗

dspErrorStatus blackManWin(uint16_t N, double w[]);
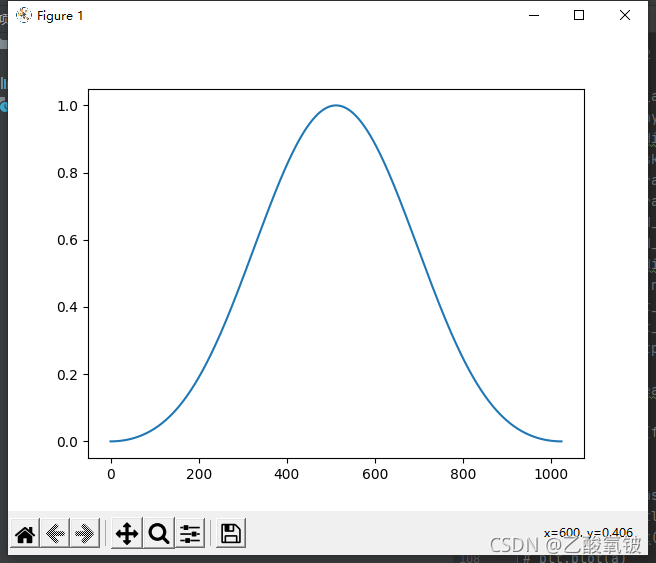
在这里插入图片描述

布莱克曼-哈里斯窗

dspErrorStatus blackManHarrisWin(uint16_t N, double w[]);
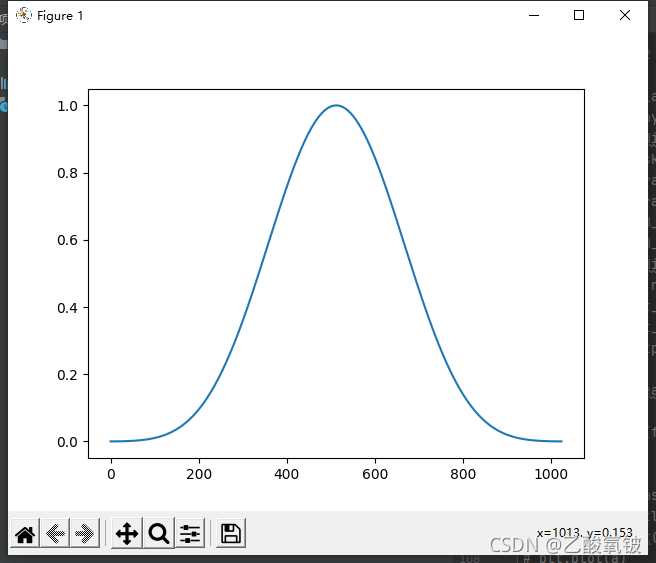
在这里插入图片描述

博曼窗

dspErrorStatus bohmanWin(uint16_t N, double w[]);
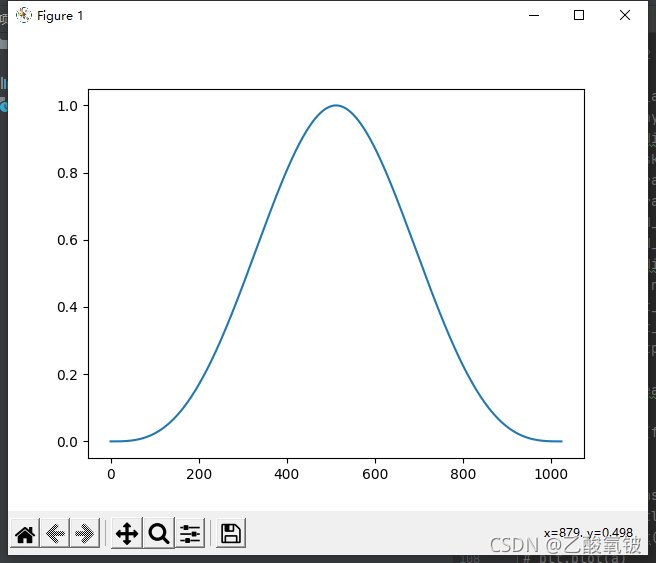
在这里插入图片描述

切比雪夫窗

dspErrorStatus chebyshevWin(uint16_t N, double r, double w[]);
r = 100 dB
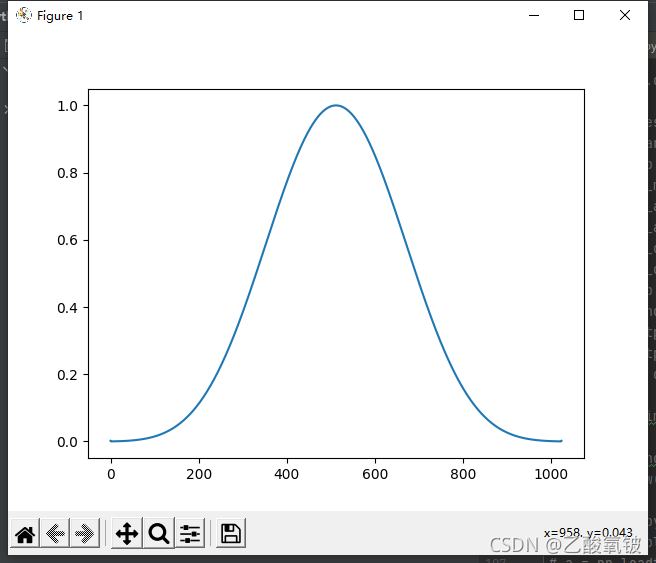
在这里插入图片描述

平顶窗

dspErrorStatus flatTopWin(uint16_t N, double w[]);
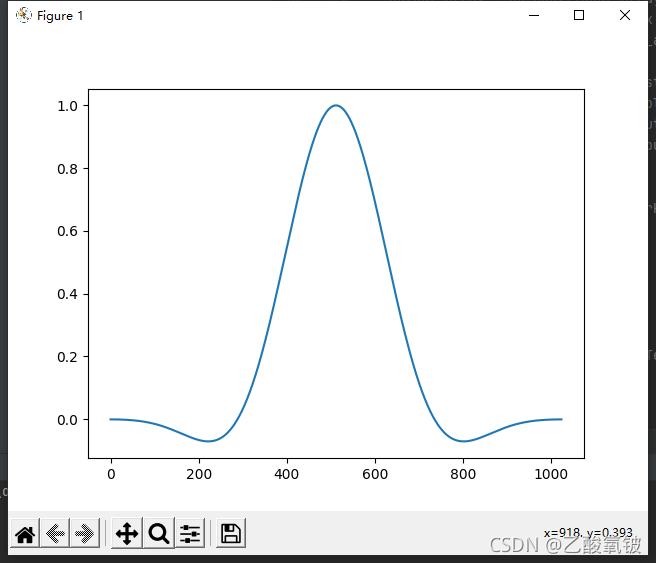
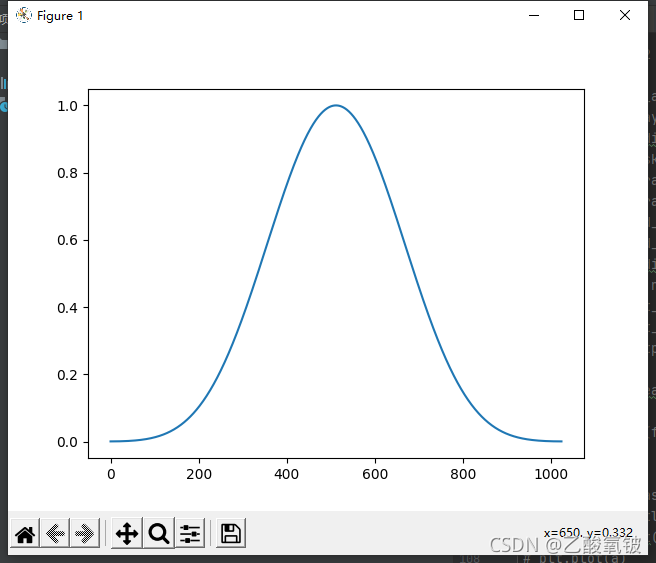
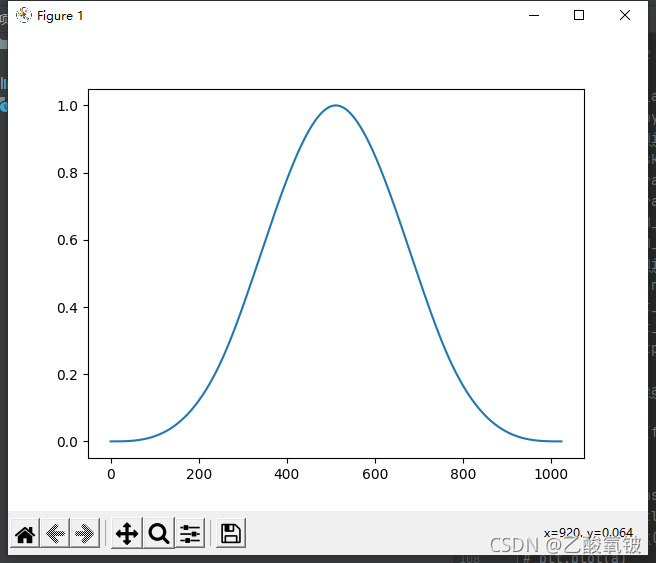
在这里插入图片描述

高斯窗

dspErrorStatus gaussianWin(uint16_t N, double alpha, double w[]);
alpha = 2.5
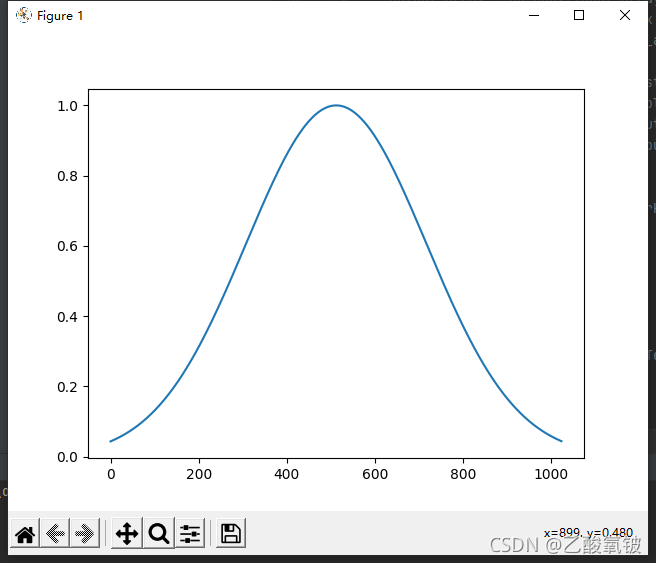
在这里插入图片描述
alpha = 8

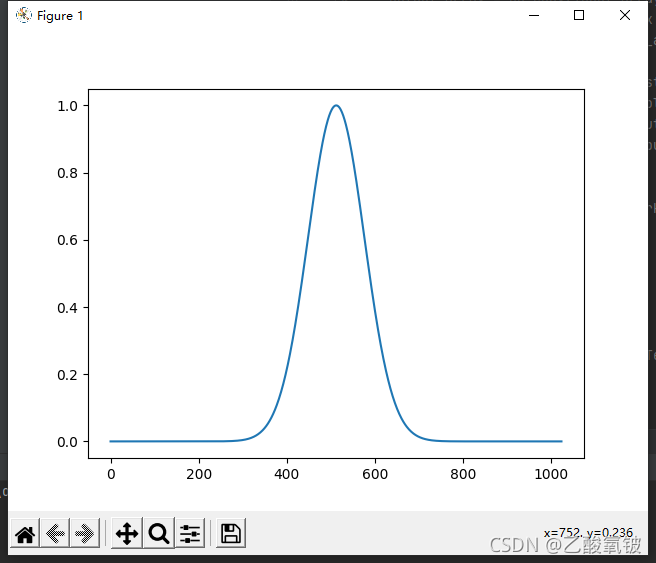
海明窗

dspErrorStatus hammingWin(uint16_t N, double w[]);
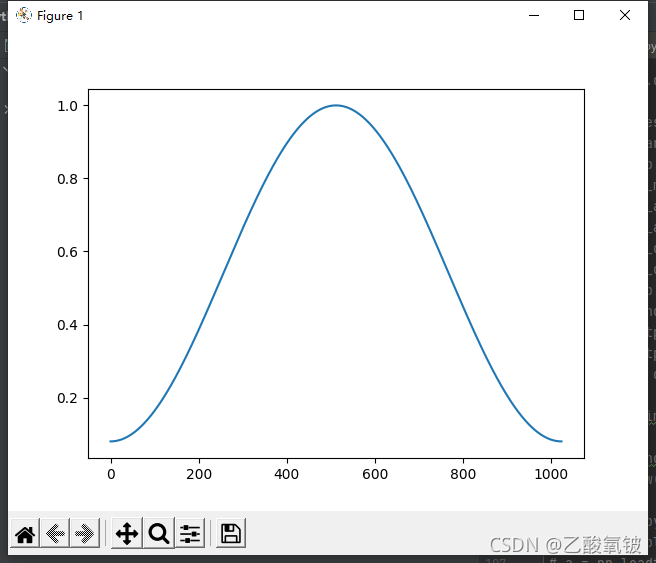
在这里插入图片描述

汉宁窗

dspErrorStatus hannWin(uint16_t N, double w[]);
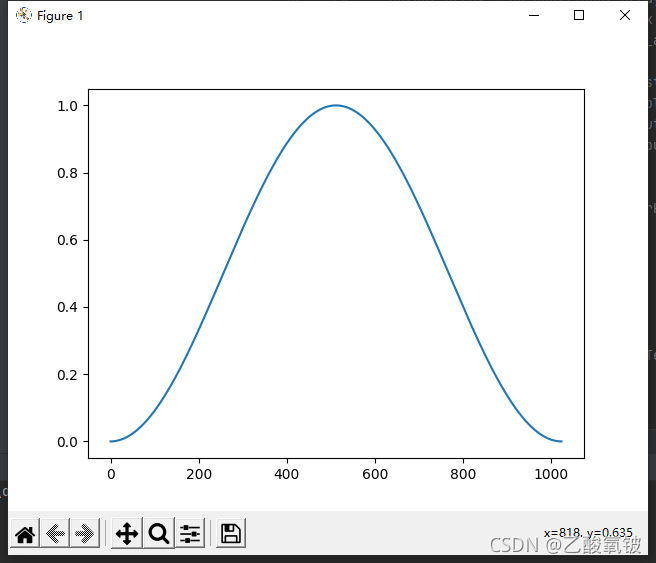
在这里插入图片描述

纳托尔窗

dspErrorStatus nuttalWin(uint16_t N, double w[]);
在这里插入图片描述

Parzen窗

dspErrorStatus parzenWin(uint16_t N, double w[]);
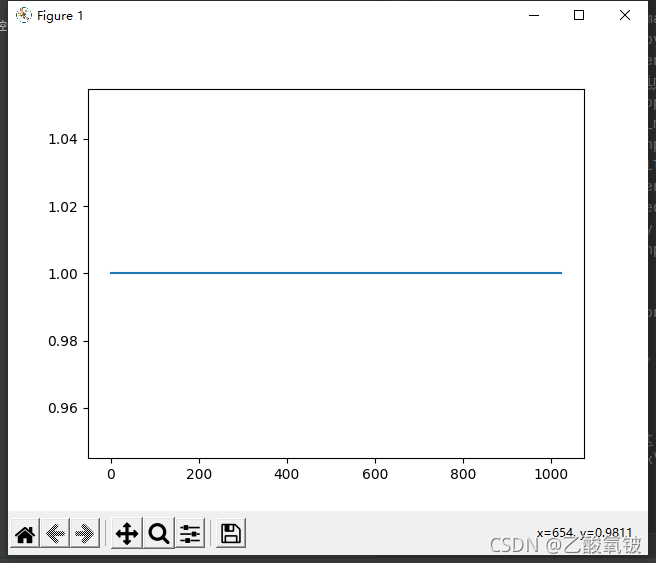
在这里插入图片描述

矩形窗

dspErrorStatus rectangularWin(uint16_t N, double w[]);
在这里插入图片描述

（模拟）效果

采样频率为100Hz
对一个振幅为2.5，24Hz, 相位为30°的方波信号进行FFT，有大小为2.5的直流偏置
1024点FFT

FFT代码见适用于单片机的FFT快速傅里叶变换算法，51单片机都能用

无窗

在这里插入图片描述

汉宁窗

在这里插入图片描述

平顶窗

在这里插入图片描述

嵌入式最新文章

基于高精度单片机开发红外测温仪方案

89C51单片机与DAC0832

基于51单片机宠物自动投料喂食器控制系统仿

《痞子衡嵌入式半月刊》第 68 期

多思计组实验实验七简单模型机实验

CSC7720

启明智显分享| ESP32学习笔记参考--PWM(脉冲

STM32初探

STM32 总结

【STM32】CubeMX例程四---定时器中断（附工

加:2021-11-11 12:52:08 更:2021-11-11 12:52:56

360图书馆购物三丰科技阅读网日历万年历 2024年11日历

-2024/11/26 9:42:15-

图片自动播放器
↓图片自动播放器↓

TxT小说阅读器
↓语音阅读,小说下载,古典文学↓

一键清除垃圾
↓轻轻一点,清除系统垃圾↓

图片批量下载器
↓批量下载图片,美女图库↓

网站联系: qq:121756557 email:121756557@qq.com IT数码

[嵌入式]常见窗函数的C语言实现及其形状，适用于单片机、DSP作FFT运算

目录

源码

WindowFunction.c

WindowFunction.h

使用

形状

三角窗

巴特利特窗

巴特利特-汉宁窗

布莱克曼窗

布莱克曼-哈里斯窗

博曼窗

切比雪夫窗

平顶窗

高斯窗

海明窗

汉宁窗

纳托尔窗

Parzen窗

矩形窗

（模拟）效果

无窗

汉宁窗

平顶窗