文章目录
0.数学模型的概念
- 什么是数学模型?
描述控制系统的输入变量、输出变量以及内 部变量之间动态关系的数学表达式。 - 为什么要建立数学模型?
对系统进行定量分析和设计的基础。 (例如,求解输出量,计算性能指标) - 数学模型的建立方法
(1)分析法:分析系统各部分的运动机理,根据它们依 据的物理规律、化学规律等列些运动方程。
(2)实验法:

人为地给系统输入端施加某种测试信号,记录其输 出响应;根据记录的输入、输出数据,用适当的数学模 型去逼近黑箱,从而建立数学模型。
(实验法所建立的模型未必能描述系统内部的运行 机理,但能描述输入量与输出量之间的动态关系。)
这也称为系统辨识方法。
4. 数学模型的类型
1)微分方程:时域
其它模型的基础 直观 求解繁琐
2)传递函数:复频域
微分方程拉氏变换后的结果
1.控制系统的时域数学模型(微分方程)
【例题1】
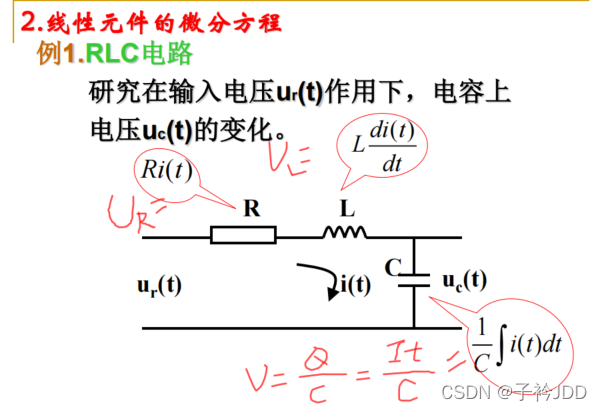


【例题2】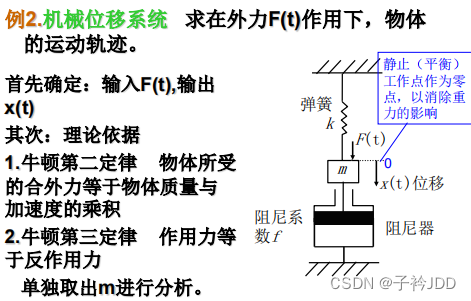


线性微分方程的一般特征
实际物理系统的线性微分方程一般具有以下形式:
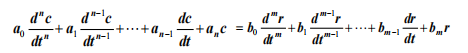
叠加原理包括:齐次性+可加性

非线性微分方程的线性化
在实际工程中,物理元件都具有不同程度的非线性。非线性微分方程的求解很困难。在一定条件下,可以将非线性方程近似地转化为线性微分方程,使对系统动态特性的分析大为简化。
线性化的方法
(1)忽略弱非线性因素 如果元件的非线性因素较弱或者不在系统非线性工作范围以内,则它们对系统的影响很小,就可以忽略
(2)在平衡点附近的小偏差法(切线法,增量线性化法)实质是在一个很小的范围内,用直线来代替非线性曲线。

方程中含有变量或变量的导数的非线性函数线性化
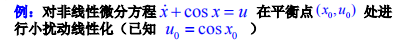

线性微分方程如何求解
拉普拉斯例题传送门
2.控制系统的复数域数学模型
2.1传递函数的定义
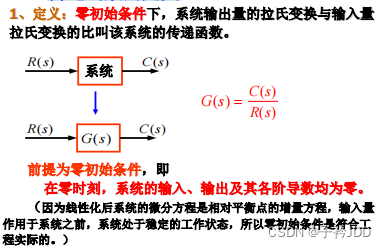
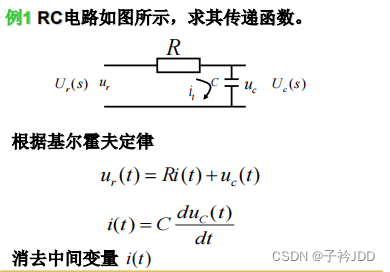
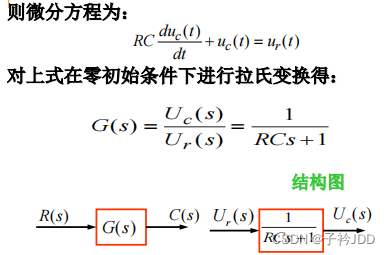

直接得

2.2传递函数的性质
(1)传递函数与微分方程一一对应;
由传递函数也可以得到微分方程,d/dt和s相互替换
(2)传递函数表征了系统本身的动态特性。
传递函数只取决于系统本身的结构和参数,而与输入和初始条件等外部因素无关。
(3)实际系统m ≤ n,分子分母多项式的系数均为实数;
(4)传递函数的拉氏反变换即为系统的脉冲响应g(t), g(t)= L-1[G(s)]。
2.3传递函数的常用表示形式
- 传递函数的有理分式形式

- 传递函数的零、极点形式(“首1”的形式)

- 传递函数的典型环节形式(“尾1”的形式)

2.4传递函数的零、极点对输出的影响
1.系统的自由运动属性(模态)


2. 极点决定了系统自由运动属性(模态)

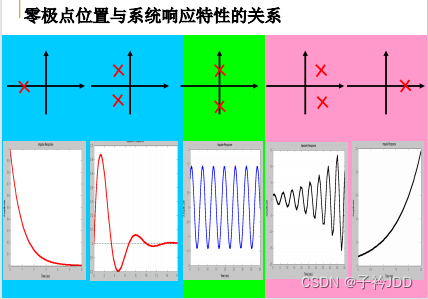
- 极点位置决定了系统响应的稳定性和快速性
(1)极点实部的负或正,决定系统是否稳定。
(2)极点实部的幅值(极点距离虚轴的位置)决定系统响应的快速性。
- 零点位置决定了各个运动模态所占的比例
(1)影响系统响应曲线的形状,影响响应的快速性。
(2)一般,零点离极点较远时,该极点对应的模态所占比例较大。反之亦然。因此,零点有阻断极点模态“激发”的作用。
2.5例题

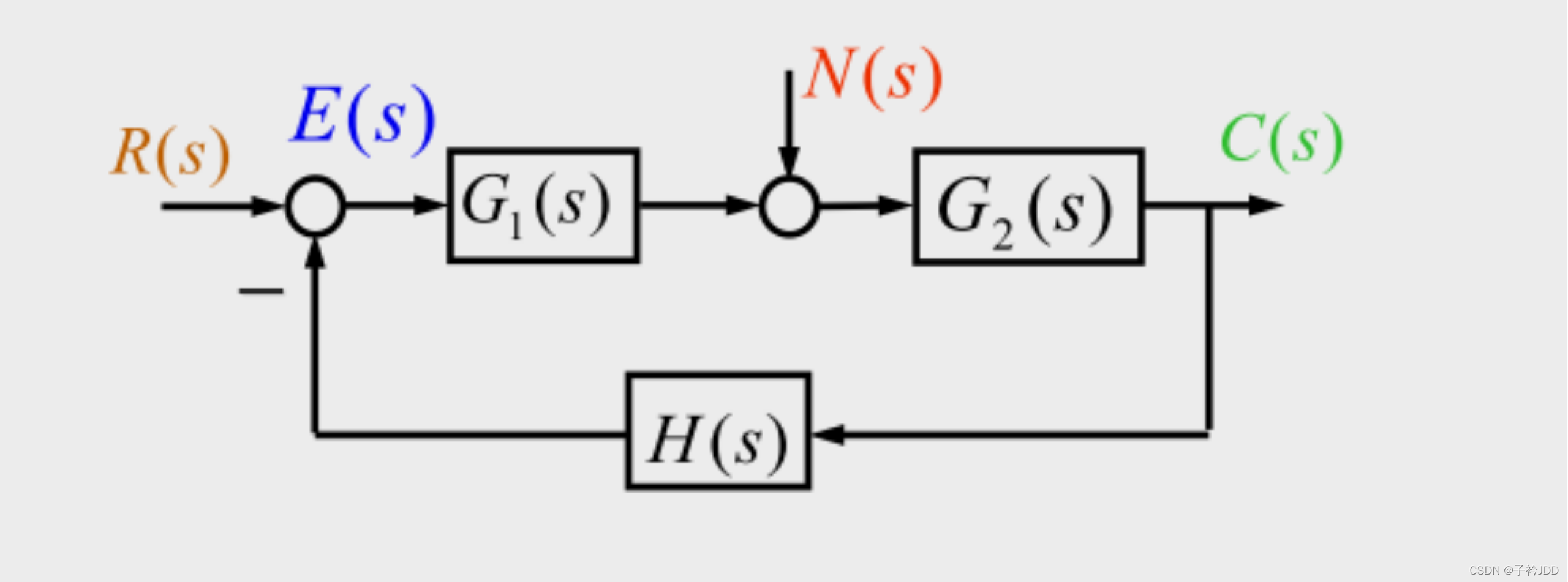
3.控制系统的结构图与信号流图
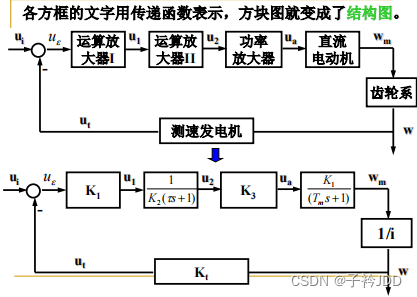
结构图绘制步骤
根据每个元件的拉氏变换方程,绘出其单元结构图。置系统的输入于最左端,输出于最右端,按照信号的流向,把各单元结构图中相同的信号连接起来,就得到整个系统的结构图.
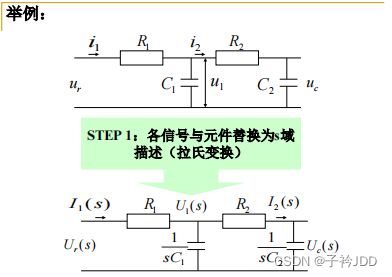
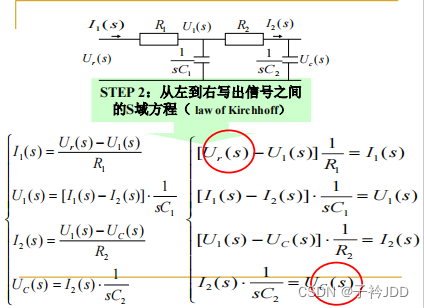
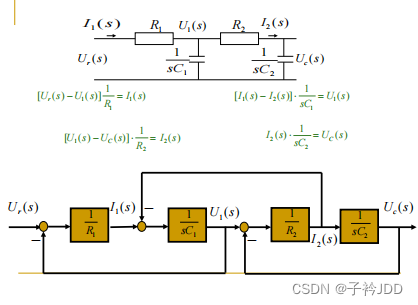
结构图的等效变换
(1) 串联
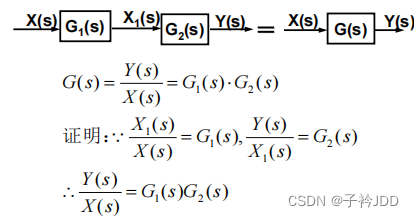
(2) 并联
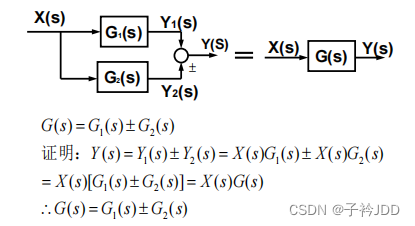
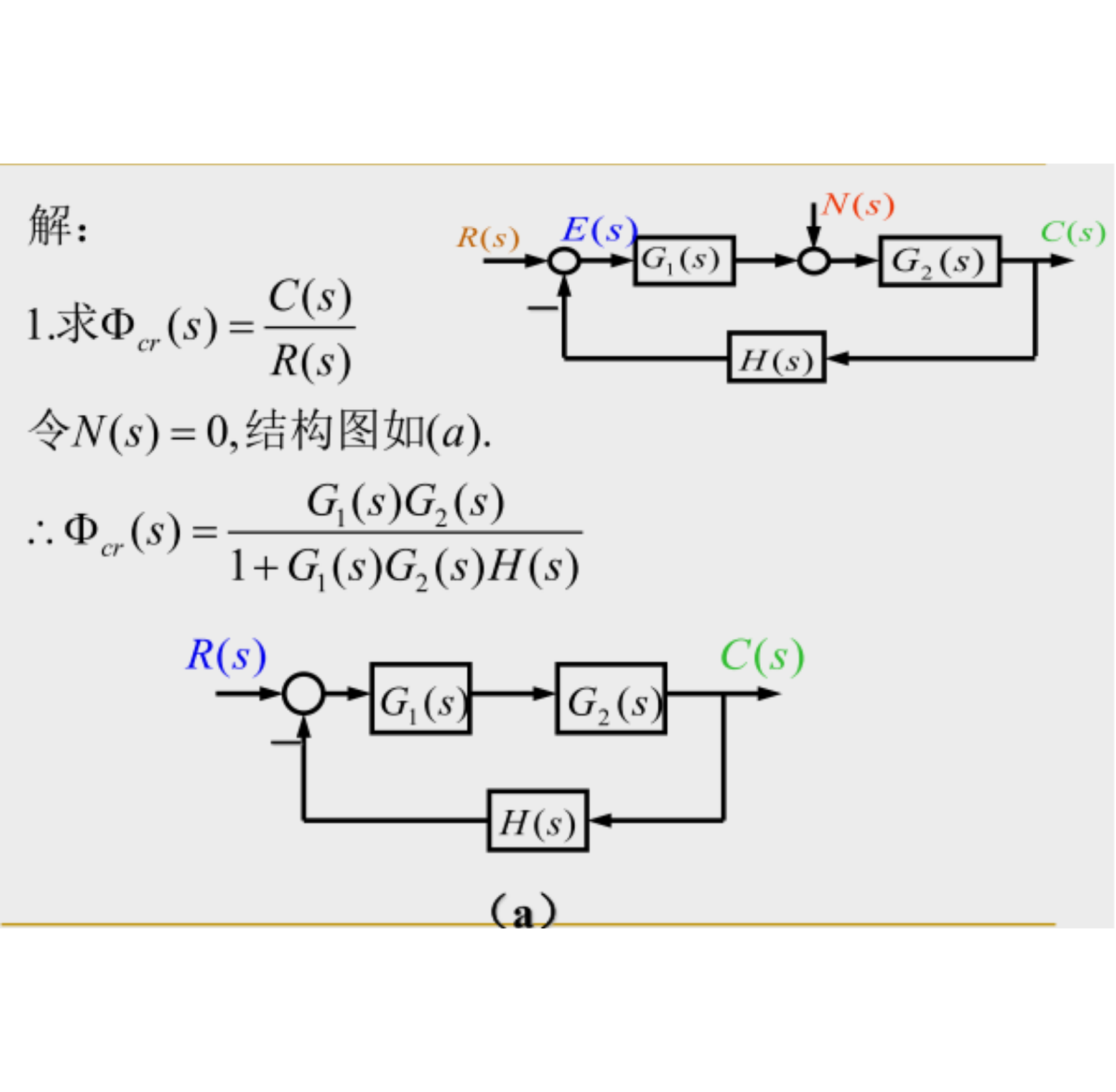
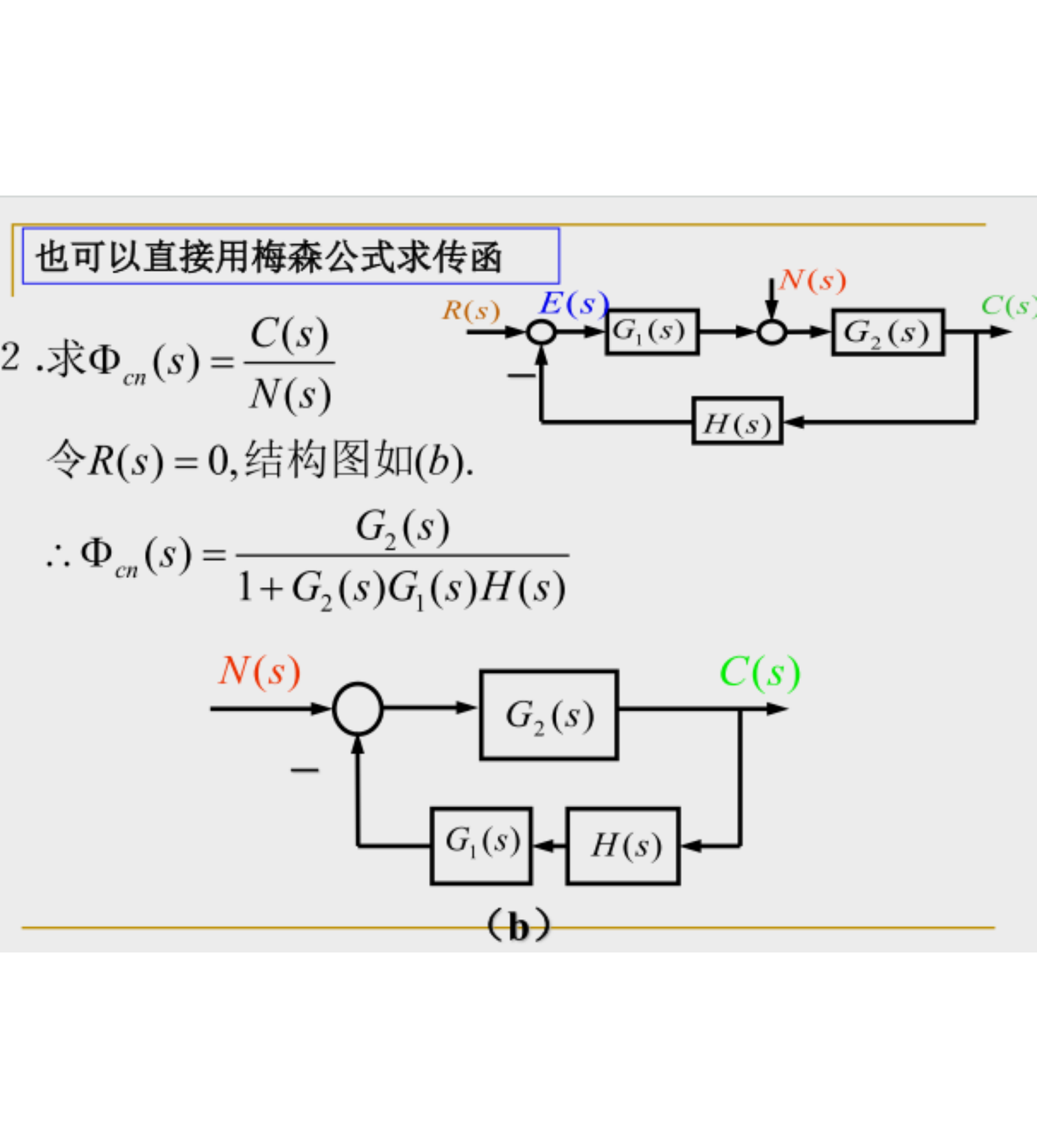
(3) 反馈
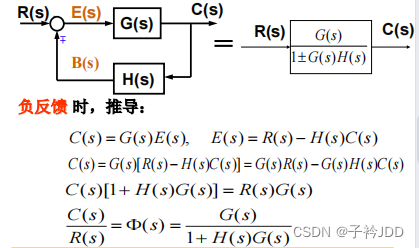


(4) 比较点和引出点的移动
一般不宜交换比较点和引出点。
“-”号可以在信号线上移动,但不能越过比较点或引出点。
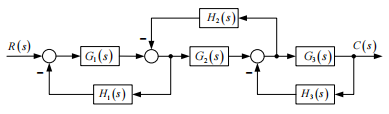
结构图例题
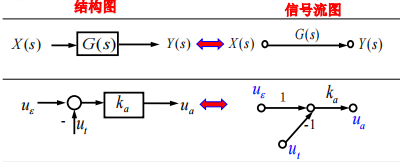
信号流图的概念和组成
组成
节点:系统中的变量(信号),用“ ”表示,同时具有叠加的作用
支路:连接节点,标上支路增益,有向线段,表示了一个信号对另一个信号的函数关系,用增益或传递函数表示(相当于乘法器)。
若增益为负数,标上“-”,为正则略。支路是有方向性的。
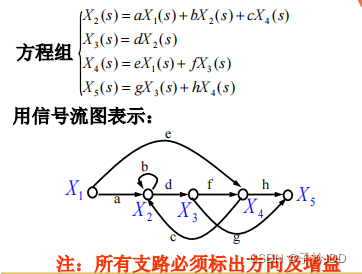
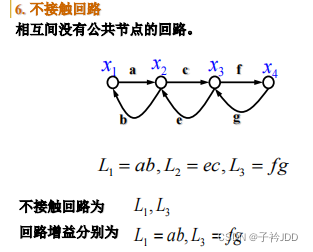
信号流图中的常用术语


梅森公式
梅森公式概念
一般采用梅森公式求信号流图的传递函数C(s)/R(s)
梅森公式也可以直接用于结构图
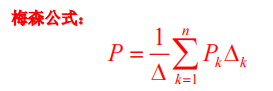
P: 输入节点到输出节点之间的传递函数(也称总增益)。
n: 从输入节点到输出节点的前向通路的总数。
Pk :从输入节点到输出节点第k条前向通路的增益。
? :信号流图的特征式:
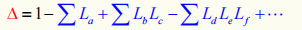

?k 第k条前向通路特征式的余因子,等于流图特
征式 ?中除去与第k条前向通路相接触的回路
增益项(相当于令其等于0)以后的余项式。
梅森公式例题
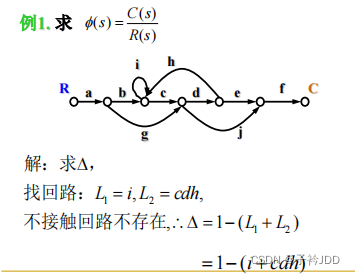
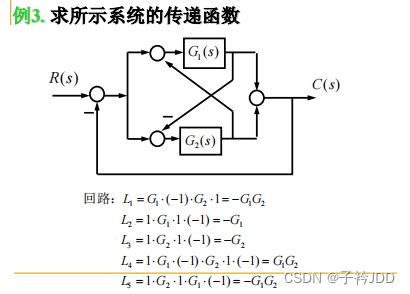
【例题1】

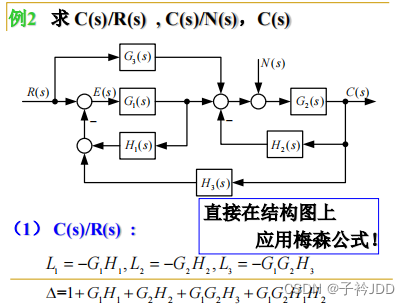
【例题2】
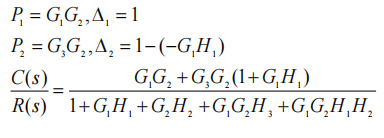


【例题3】

【例题4】
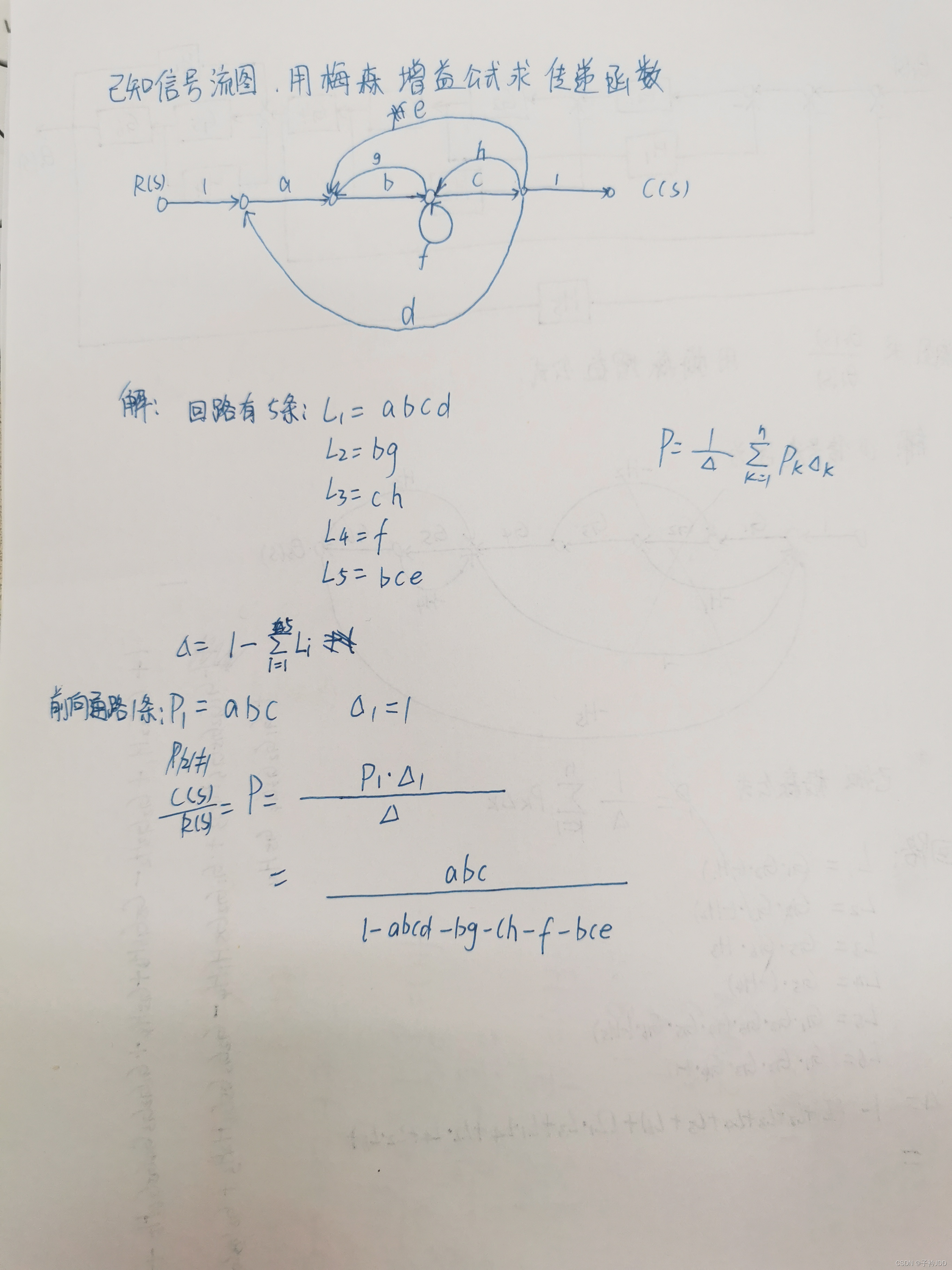

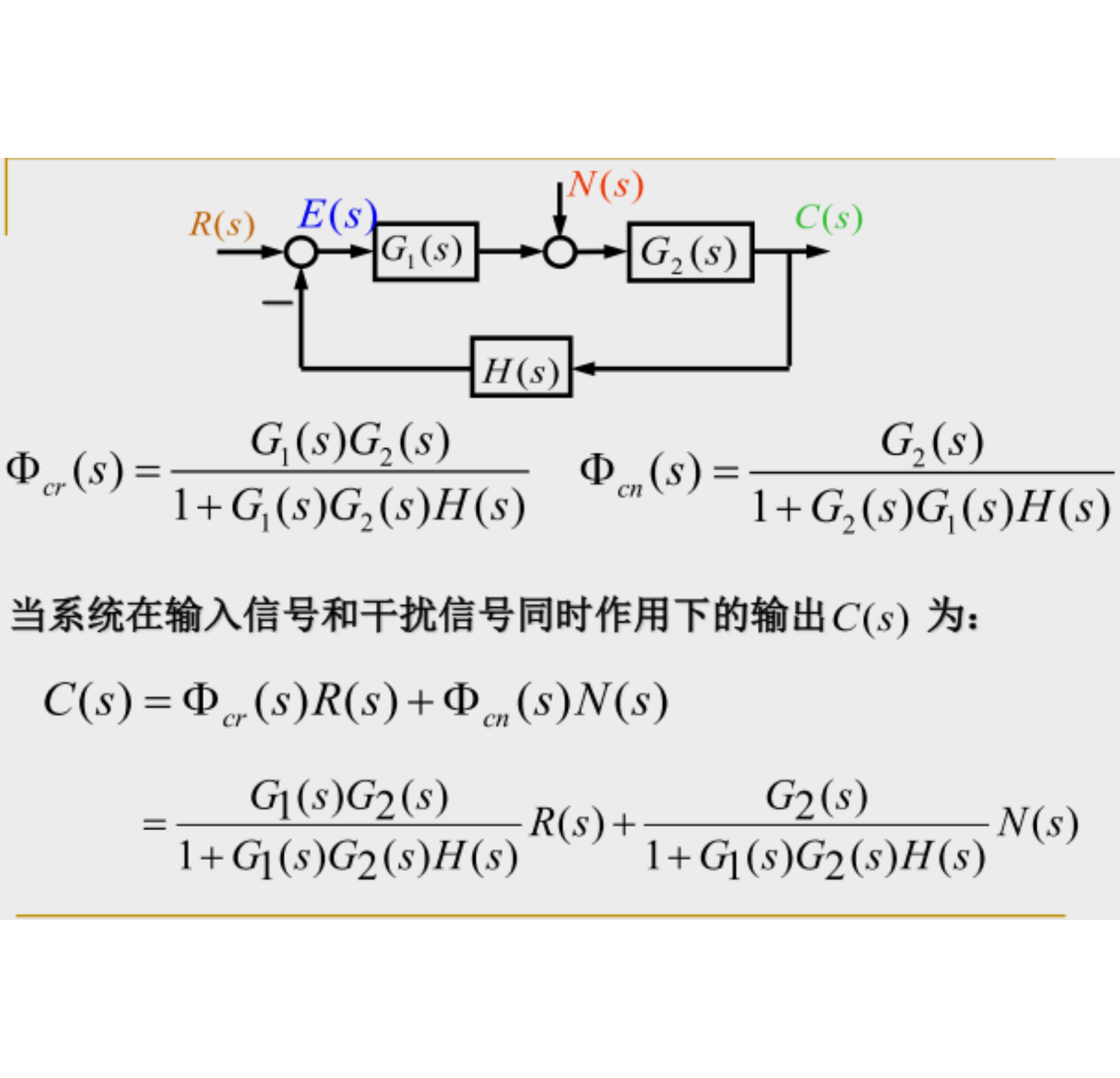
闭环系统的传递函数