前言
之前已经记录了一些有关智能车硬件、方向控制、电机控制以及图像方面的内容,说了好几次在后面会出一篇有关PID的文章,今天填一下自己挖下的坑,本篇文章主要记录一些与智能车有关的算法,参考书籍是《计算机控制技术与应用》(第二版)。
计算机控制系统
老套路,还是先引入部分理论知识。计算机控制技术包含着两部分内容:一是计算机控制的理论基础;二是实现技术,主要包括通道接口技术和系统实现技术。1

单片机作为一种微型计算机采用的是数字信号,而智能车在运行过程中的大多数物理量都是模拟量的形式,因此二者直接必须采用模/数(A/D)转换器和数/模(D/A)转换器,已实现两种信号的相互转换,在整个控制系统中单片机根据给定输入信号、反馈信号和系统的数学模型进行信号处理,实现其控制策略,通过执行机构控制被控对象,达到预期控制目标。其典型结构如下图所示:

有关整个智能车系统的各个组成部分,之前的方向控制和电机控制已经介绍过了,在此主要是记录一些常用的控制规律、过程通道以及抗干扰技术。
常用控制规律
PID控制
在了解PID控制之前,我们需要弄清楚为什么要用PID控制?
举例来说,电热水壶大家肯定都用过,每次想喝水就会用它把水烧开,在这里烧开是我们的期望值,当水温达到100度时水壶判断水已经烧开了会自动跳闸,跳闸后水温会逐渐降低,并不会一直保持在100度,这种情况就是一个开环的控制,系统可以使被控量达到我们的期望值,但是无法一直让被控量保持在期望效果;如果我们想让水温一直恒定在指定温度,就需要使用到PID,通过合理地PID控制就可以保持水温一直处于我们期望的温度。接下来我们来了解一下PID到底是个啥。
这里先补充一点自动控制原理的相关概念:
如图所示,自动控制系统中期望值或者说给定量是1(单位阶跃信号),而输出量的波形如下图橙色曲线所示,这里有几个相关的指标名称需要大家做个了解,分别是超调量和调节时间,超调量从一定角度反映了系统的稳定性能,一般我们希望超调量越小越好,调节时间ts,它是指输出曲线进入并一直保持在5%误差带内所用的时间,对于一般的系统我们都希望这个调节时间越短越好。


PID控制包括比例(P)、积分(I)、微分(D)3种控制规律,由这三种控制规律可以组合成P控制器、PI控制器、PD控制器、PID控制器等。需要注意的是它们都是线性控制器,工作原理都是根据给定量r(t)与实际输出量c(t)之差[e(t) = r(t) - c(t) ]形成控制量,进而去控制被控对象,是对象输出趋于给定。

比例(P)控制器
比例控制的原理是将偏差e(t) = r(t) - c(t) 乘以一个比例系数Kp,计算结果作为控制量输出到被控对象上,实现闭环控制。
其控制规律如下:
u(t)=Kp×e(t)
当Kp=0.297 Ki = Kd = 0时,

当Kp=0.1 Ki = Kd = 0时,

当Kp=0.4 Ki = Kd = 0时,(收敛振荡)

当Kp=0.472 Ki = Kd = 0时,(等幅振荡)

当Kp=0.5 Ki = Kd = 0时,(发散振荡)

对比上面几个给定量与输出量可以看出,比例控制在合理范围内能使系统输出维持在一个稳定的范围,例如
当Kp=0.1 Ki = Kd = 0时,系统输出大致稳定在0.5左右,
当Kp=0.297 Ki = Kd = 0时,系统输出大致稳定在0.75左右,
显然这里的输出和实际期望1之间存在一定的差值,这个差值被称为静态误差,静差的产生是由于比例控制器本身是靠偏差工作的,若偏差消失[e(t)=0],控制器作用也就消失[u(t)=Kp×0=0]。对比Kp取值的不同可以发现,Kp取值越大这个静差就会越小,但是当Kp超过一定范围后(如上图Kp>0.4时)系统的性能会被破坏,会引起被控量的振荡导致系统不稳定。
因此在系统控制中很少单独使用比例控制器进行控制。
比例积分(PI)控制器
为了消除比例控制的静差,可以采取在比例控制的基础上增加积分控制,形成比例积分控制器,其控制规律如下:

其中Ti为积分时间常数,下图表示的是PI控制器对于阶跃信号的时间相应,比例部分好理解,就是一个倍数关系,而积分部分,由于是阶跃信号,相当于e(t)是个恒定值A,在高数中,对一个数积分后是一个一次方程Ax+b的形式也就是下图中斜线;可以看出PI控制器的输出分为了两部分,一部分是比例作用,与偏差成正比;另一部分是偏差的积累,即积分作用。只要e(t)不为零,积分部分就会一直累计,从而影响控制量u(t),以此减少偏差,直到偏差变为零,系统进入稳态。

当Kp
智能车速度开环
比例积分微分(PID)控制
积分作用的加入,虽然可以很好地解决静差的问题,但代价是降低了系统的响应速度,系统达到稳态的时间(调节时间)变长了,对于一些对调节时间要求较高的系统来说就不适用,类似于舵机控制,如果调节时间太长会出现明显的舵机打角延迟,为了解决这一问题,就需要引入就有超前特性的微分D(高数中的求导,求变化率)控制,这样就组成了PID控制器。
当Kp=0.297, Ki = 0.0085,Kd = 0时,系统振荡不稳定

当Kp=0.297, Ki = 0.0085,Kd = 1时,调节时间ts=700ms;

当Kp=0.297, Ki = 0.0085,Kd = 3时,ts=180;

对比可以发现D的加入可以有效地缩短调节时间ts,使得系统更快的到达稳态。
位置式PID
令T为采样周期,以一系列采样时刻点kT代替连续时间t,用和式代替积分,以增量代替微分,则可得到以下控制规律:
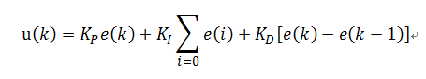
位置式PID控制算法的程序框图如下:

从表达式中可以看出积分部分是一直在累加,这个过程可能会导致积分饱和,影响整个系统的控制效果。
增量式PID
除了位置式的PID还有一种增量式的PID,其控制规律如下:
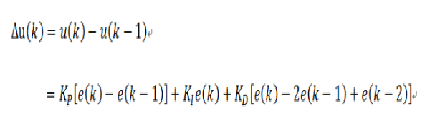


从表达式中可以看出增量式PID是利用当前误差和过去两拍的误差来做计算,整个计算量比位置式要小且不会受到以往太多参数的干扰。
有关位置式PID与增量式PID的选取、优缺点及代码参考这篇博文,传送门。
数字PID控制算法的改进
应对不同的实际系统,我们还需要针对系统的特点对PID进行改进,例如对于控制精度要求不高,但对系统的平稳性要求较高的系统,可以采用带有死区的PID控制方式。类似做了特殊处理的还有积分分离式PID、不完全微分的PID、微分先行的PID等,这里不再一一介绍,感兴趣的同学去查看我上传的PPT介绍。
PID参数整定
有关PID的参数整定,分为两大类方法,一类是理论设计法,此法需要知道系统的数学模型,对于智能车来说实现起来有难度;另一类是实验确定法,实验法中又包括有试凑法、扩充临界比例法、扩充响应曲线法等。
智能车调参中常用的是试凑法和扩充临界比例法,采取先调比例,后调积分最后加微分的方式,有关参数整定的具体步骤介绍的PPT我已经上传到资源需要的同学自行下载。
小结
PID中三个参数对系统的影响各有不同,主要介绍如下图所示。另外前文中使用的simulink仿真模型也已经放到资源里了,需要的同学可以自行领取。



串级控制
串级控制的结构框图如下图所示,串级控制系统在结构上有两个闭环,一个在内被称作副回路,在控制过程中起到“粗调”的作用;一个环在外面,起到“细调”作用被称为主回路。考虑到篇幅问题有关串级控制的详细介绍也请大家自行查阅,在此不做介绍了,在比赛中,一般是直立车会采用这种串级PID控制的方式,使用串级控制可以很好地改善系统的控制质量。

模糊控制
模糊控制是智能控制的主要方式之一,其特点是不需要建立对象的数学模型,依赖规则库进行控制;控制规律采用自然语言,能够很好地利用人的经验。

模糊控制器由模糊化、知识库、模糊推理机、清晰化四部分组成,模糊控制的使用类似于我们日常生活中形容一个人身高的高、中、低年龄的老、中、青,这些都没有一个明确的界限,是根据自己的经验进行判断的,大致思路就是计算出当前误差在每个模糊集合里面的隶属度,根据隶属度来确定输出。这种控制技术被公认为简单而且有效。对于模糊控制,想要深入了解的同学还是自行了解吧,不会模糊控制的同学,用好分段PID也能跑出不错的成绩。
计算机控制技术与应用 刘国荣,梁景凯主编 .——2版.北京:机械工业出版社,2008.1 ??