[嵌入式]Part-Ⅰ2. 稳态变换器分析原则（三）

2.5 含双极点低通滤波器的变换器输出电压纹波估算

• 在分析包含双极点低通滤波器的变换器（如cuk、buck）的输出时，小纹波近似理论将会失效。对于这些变换器，无论输出滤波电容取多大，其电压纹波的小纹波近似都是0。
• 为什么产生上述情况呢？因为这时输出电容上的电流分量是由电感电流的纹波产生的，因此在计算电容电压纹波时，电感电流的纹波不能忽略，且要更为精确的近似值。
  
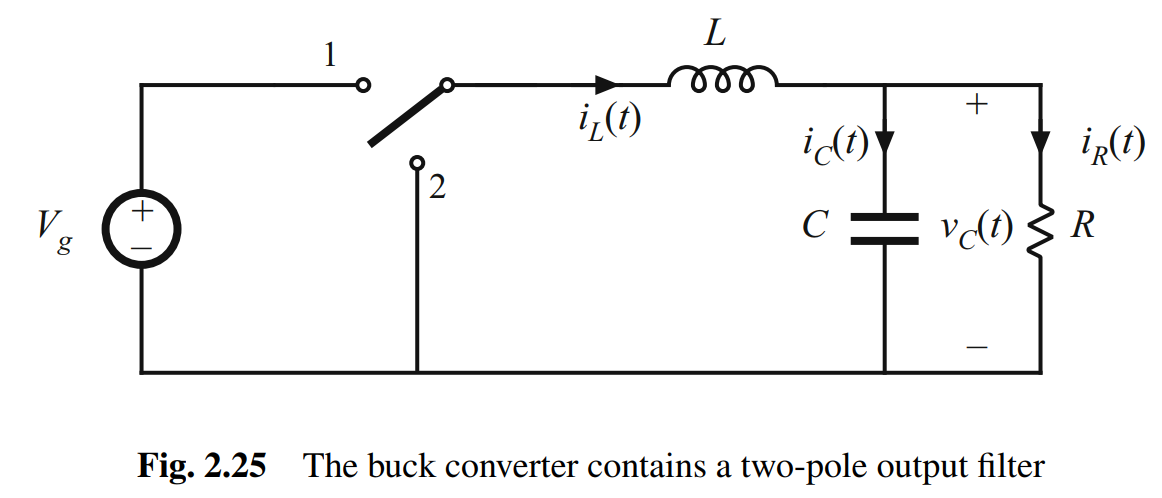• 如图所示buck电路，电感电流波形$i_L(t)$包含一个直流分量 $I$以及峰峰值为$2\Delta i_L$的交流分量。
  
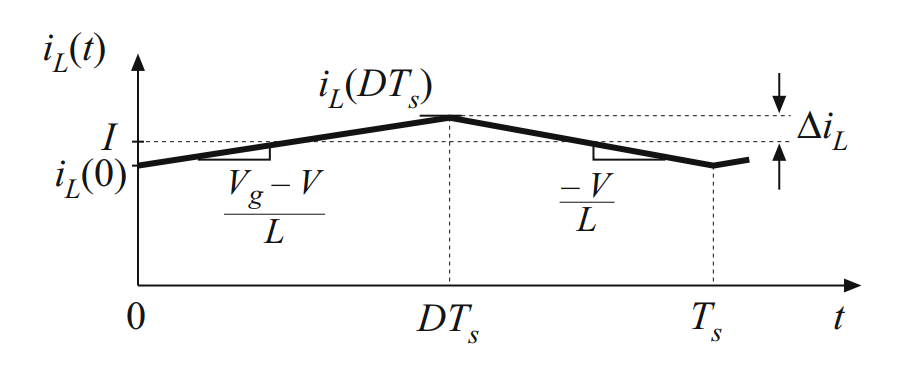• 考虑理想情况下，直流分量全部流入负载电阻，同时，交流分量在负载电阻和滤波电容之间分配。在一个设计良好的变换器中，电容对开关纹波进行了有效的滤除，电容C的选择足够大，使其在开关频率下的阻抗远小于负载电阻。此时，几乎所有的电感纹波都流经电容，很少的纹波电流流过负载。
  
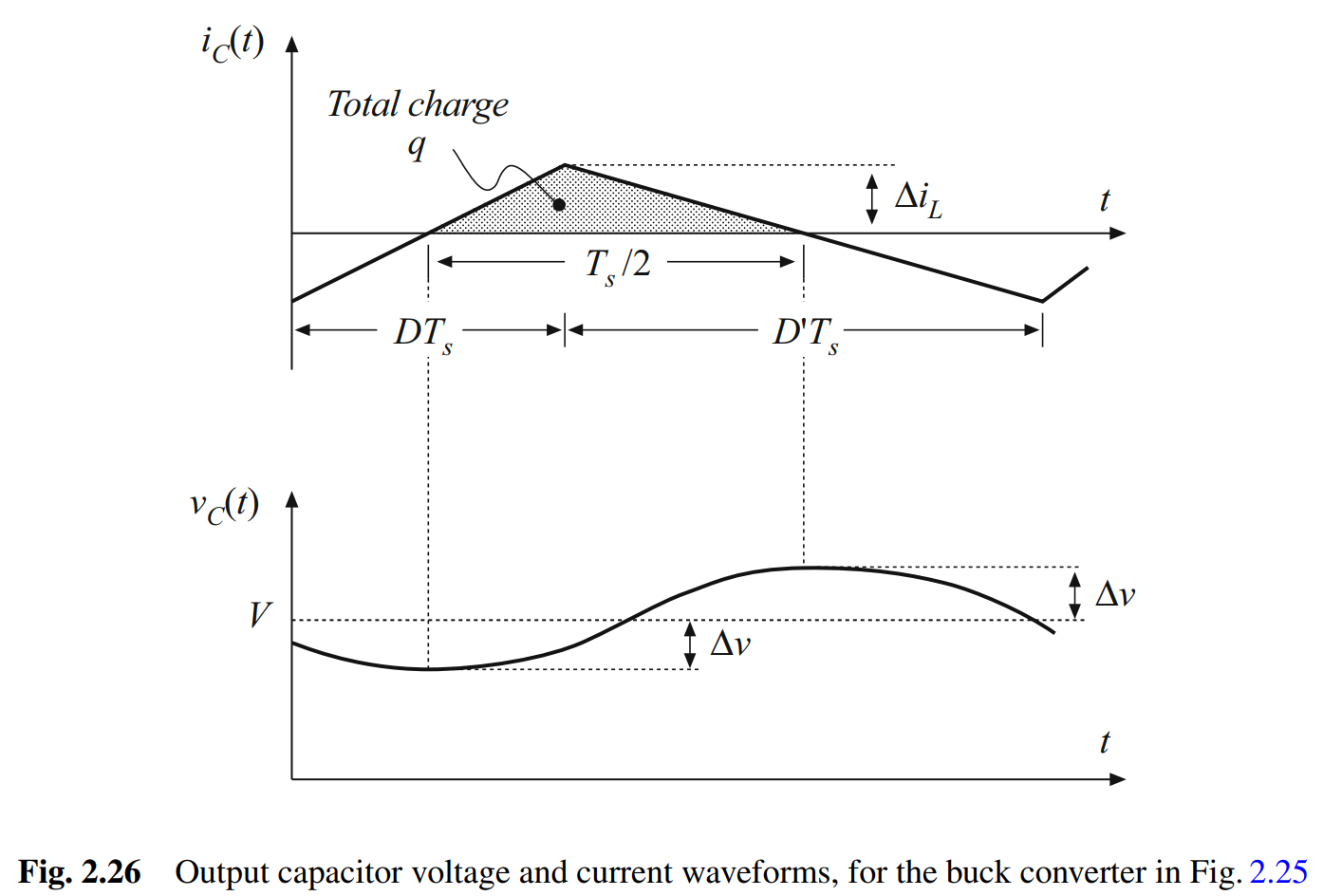• 当电容电流$i_C(t)$为正时，电荷存储在电容板上，电容电压增加。因此在电容电流两个过零点之间，电容电压在最大值和最小值之间变化，且波形是对称的，电压$v_C$的总改变量就是电压纹波的峰峰值，即$2\Delta v$。
• 通过电容公式 $Q=CV$ 可得 $$q=C(2\Delta v)$$
• 而电荷q是电容电流波形的两个过零点之间的积分，也就是阴影三角形的面积。因此有 $$q=\frac{1}{2}\Delta i_L\frac{T_s}{2}$$
• 电压纹波峰值 $\Delta v$可以求得 $$\Delta v=\frac{\Delta i_L}{8C}{T}_s$$
• 这个等式可以用于选择C的值，从而获得给定的电压纹波大小。实际在使用时，还得考虑电容的ESR等因素。
• 类似的方法也可以用到电感，如下图，将一个双极点滤波器加到buck变换器的输入端，此时电容电压的纹波不可忽略。
  
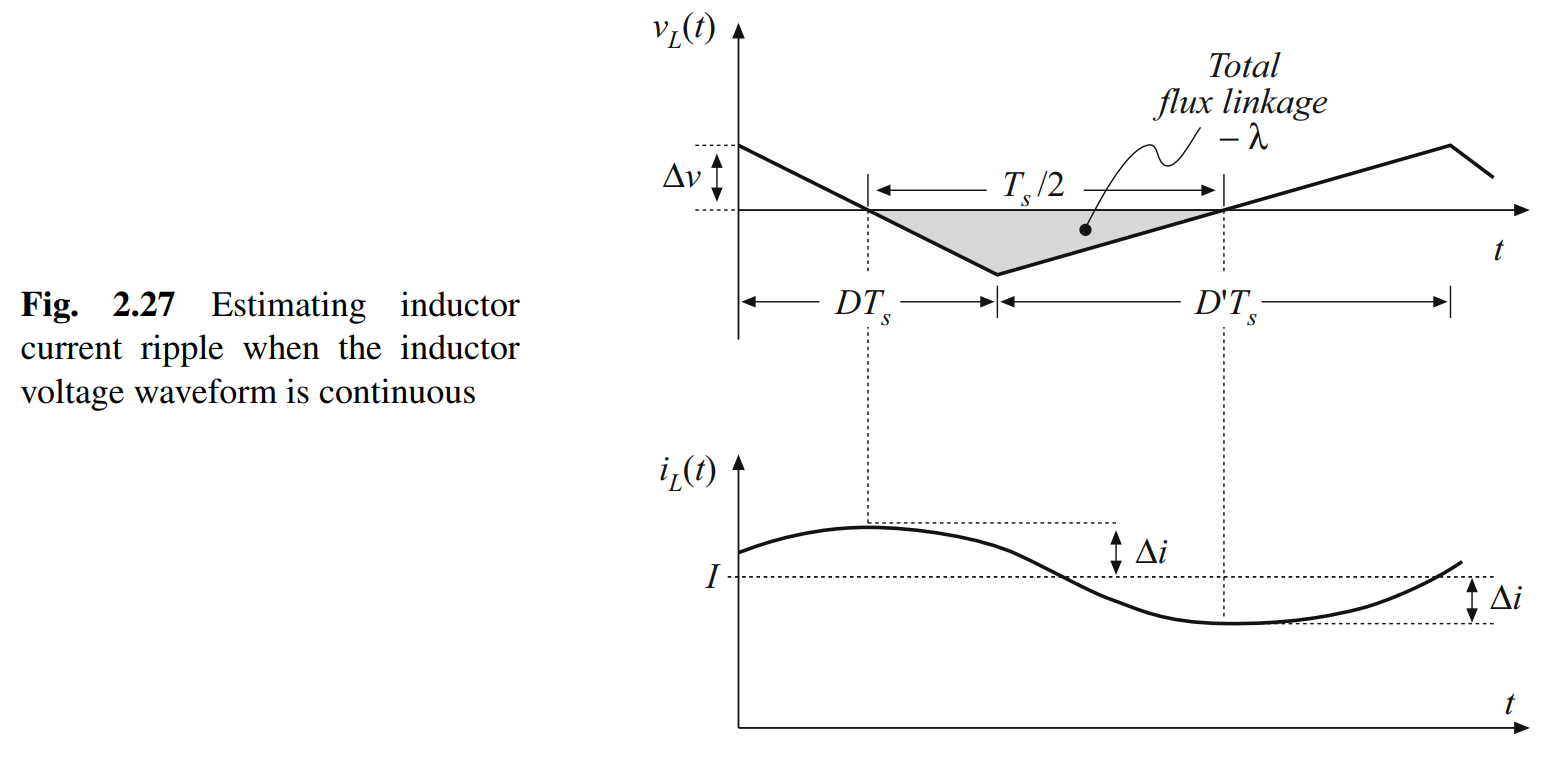
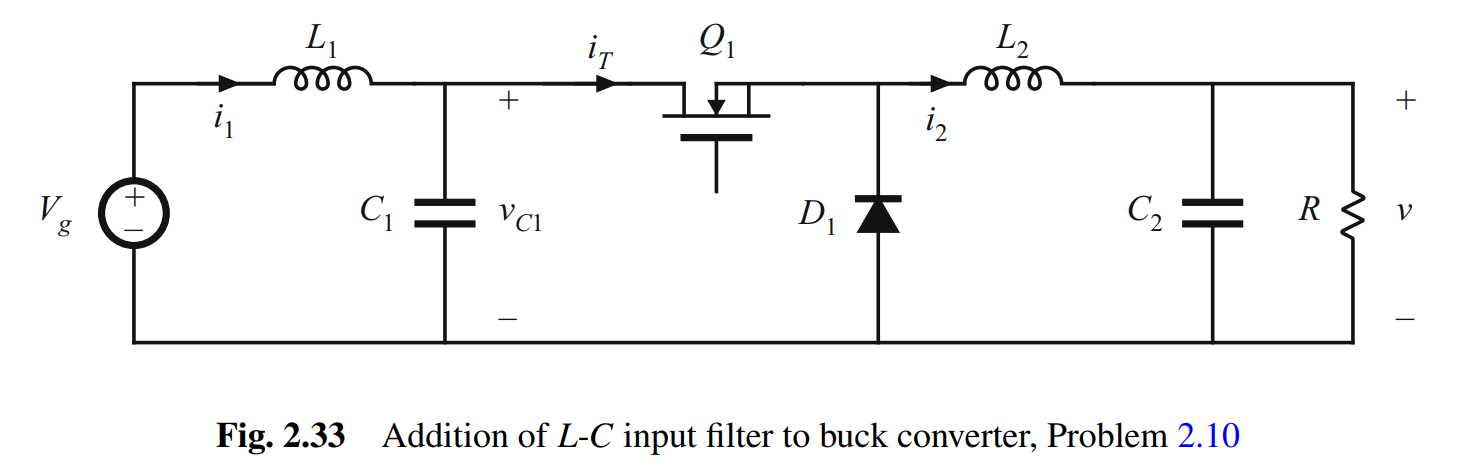• 实际电感器电压波形与输入滤波电容电压的交流部分，具有线性纹波和峰峰值。通过使用电感关系 $\lambda =Li$，可以得到类似结果。

2.6 要点小结

• 变换器波形的直流分量由其平均值或一个开关周期的积分值除以开关周期时间得到。
• 小纹波近似简化了分析过程。在良好设计的变换中，与相应的直流分量相比，电感电流与电容电压中的开关纹波比较小，可以忽略不计。
• 电感的伏秒平衡原理可以确定任何开关变换器中的电压直流分量。在稳态下，施加到电感的平均电压必须为0.
• 电容的电荷平衡原理可以确定任何开关变换器中的电流直流分量。 在稳态下，流经电容的平均电流必须为0.
• 通过求解电感电流和电容电压波形的斜率，可以计算出交流开关纹波幅值，可以根据确定的纹波要求选择相应的电感、电容。
• 在包含多极点滤波器的变换器中，连续（无脉动）的电压或电流施加在一个电感或电容上，这些元件中的交流开关纹波的计算可以使用电感器的磁链参数或电容器电荷参数完成，无需使用小纹波近似。