LC谐振高频逆变电路

$\qquad$ 写在前面：最近要做一个1Hz~400kHz的高压大功率功率放大器，看了一些文献，主要就关于多电平并联逆变器的，其实做大功率的功放也相当做一个高频逆变电路。另外将之前画的BMS的电路板PCB截图分享出来。需要原理图和PCB原版的可以留言。废话不多说，今天主要分享将高频方波电源接LCR串联支路，在一定参数下，可以使得电流成正弦波。

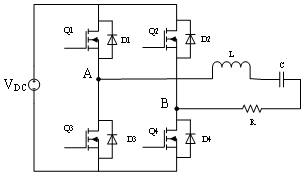
全桥电路

在这里插入图片描述

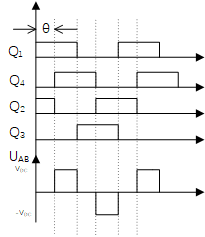
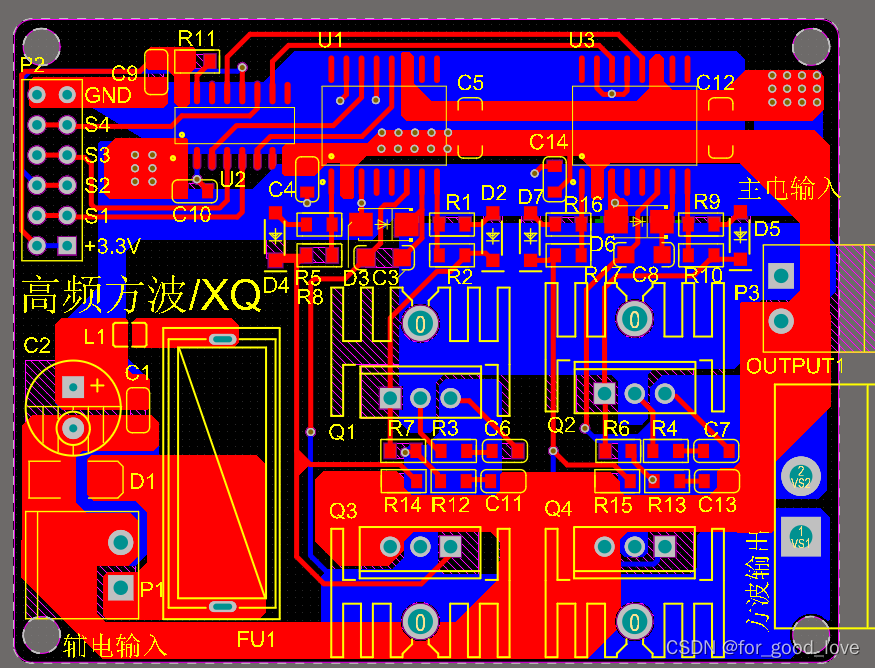
$\qquad$ 上图是全桥电路，基本原理不用说，保证上下管不直通即可，若Q1和Q4接相同信号，Q2和Q3接相同信号，则UAB是标准方波信号，此时进行傅里叶分解也比较简单。若Q1和Q4，Q2和Q3接不同信号，一般称为移相全桥电路，UAB＝UA-UB，通过设置移相角，就可以改变UAB大小（三角形运算）当然还可以直接通过改变占空比大小来改变输出幅值。值得一说的是，大多数文献是将移相全桥电路用在DCDC变换器，与这里电路不同的是有一个高频变压器，这里不细说。顺便附上一张全桥电路的PCB图，注意高频走线的回路。
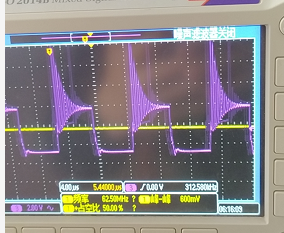
$\qquad$ 高频回路有电感效应，相当于通电线圈（这里也说一下采样康铜丝（螺旋的那种）采集交流信号或者电感的高频电流信号时也会有这个问题），如果不注意走线，就会出现下面的波形（100kHz）。
在这里插入图片描述
$\qquad$ 这应该是内部寄生电容（Cgs）和高频走线回路的电感引起的谐振吧。（等震荡问题、开通关断延时问题、软开关问题出现较多时想写一写MOS管相关的东西），解决方法有：**1、**增大Rg减小震荡，但貌似效果不太行。**2、**增加snubble电路，即在DS间增加RC电路。适量改变RC的值可以适量减小震荡，但空载损耗会加大，这是很显然的。**3、**重新打一次板子吧
在这里插入图片描述

D类和E类功率放大器

D类功率放大器

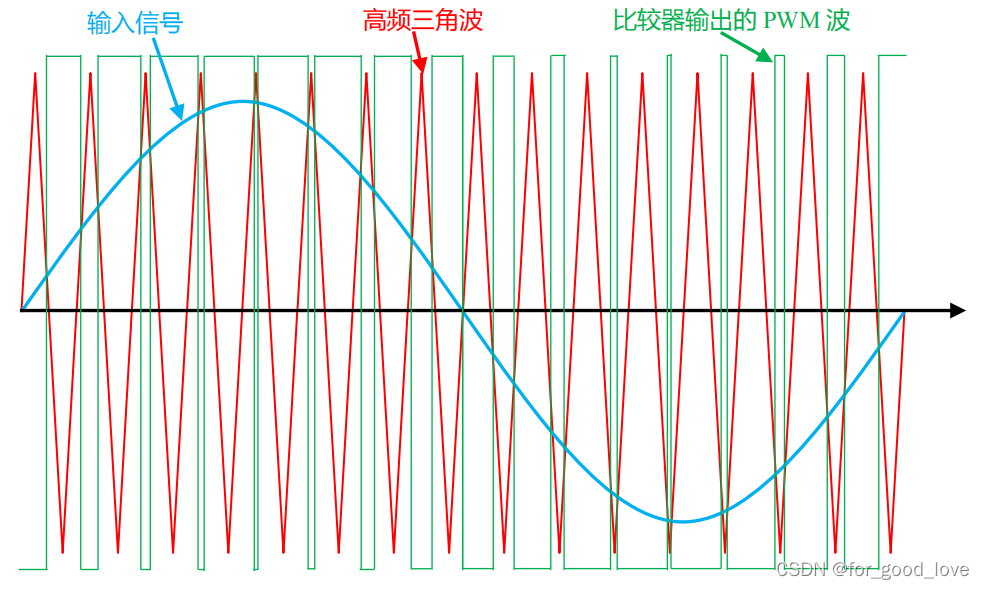
$\qquad$ D类功放器是传统功放大功率功放中效率很高的放大器了，其效率远高于甲乙类功放（我这做了一个对称结构的甲乙类功放的仿真，对管中没有P管，且驱动电流由主电路给。但仍然存在效率、发热等问题），但波形质量肯定不如AB类功放，D类功率放大器的效率之所以高，原因在于他将管子用在饱和导通区，即开关状态，而甲乙类功放是用在可变电阻区。D类功放器在某种程度上可以认为是两电平的逆变器，其开关管的调制方式也是SPWM调制方式。既然调制方式是SPWM，那么就存在着两电平SPWM逆变的天然缺点，主要有2点：1是输出LC滤波器设计较为困难，通常一级LC滤波只能设置某一个频率。比如设置的LC滤波参数在高频1kHz的时候输出波形THD较小，那么低频的时候波形就很’粗‘，如果截止频率设置较低，低频段波形较好，那么高频段衰减严重…2就是通频带的问题，一般而言，载波要是调制波的50倍以上才可以滤波出比较好的波形，对于音响级别要做到上百倍以上。目前市场上的D类功率放大器带宽最大是5kHz（2020年的一篇文献中看到的），这意味着载波频率fs（开关频率fr）要达到250kHz，这就又要涉及到软开关的技术了，这里不讨论了。（所以目前这个400kHz的功放再看多电平逆变方向看文献，也不知道对不对。）

D类功放调制方式

E类功率放大器

$\qquad$ E类功率放大器和D类很类似，但管子数量少于D类功率放大器，输出滤波较D类功率放大器而言多了一级，有很多关于一级LC滤波和两级LC滤波的文献，可以找出来看看。DE类功放肯定结合了两者的优缺点，在各种新能指标中进行trade-off。分享DE类功率放大器中有一些假设，其中有一个比较重要的假设就是，假设系统中的品质因数（特征阻抗与串联支路阻抗之比 $Q=\frac{1/wc}{R}=\frac{wL}{R}$ ）足够大，即阻尼系数足够小。下面看看原因

LCR串联谐振电路

$\qquad$ LC谐振都知道 $w=\sqrt{\frac{1}{Lc}}$ 时谐振，且谐振之后串联支路阻抗 $Z_L=wL-\frac{1}{wc}+R=R$ ,那么此时为啥电流就是正弦了呢？不应该还是方波吗？因为支路纯阻性了不是吗？请注意，书上说的支路显阻性是在正弦电源激励下才会出现 $Z_L=R$ ，这时应该利用傅里叶级数去分析。这个后面讨论。
$\qquad$ 这里的参数是 $L = 3 m H, c = 843.343 p F, R = 2, f s = 100 k H z$
$\phi(jw)=Arg(Z_{jw})=arctan\frac{wL-\frac{1}{wc}}{R}$

在这里插入图片描述

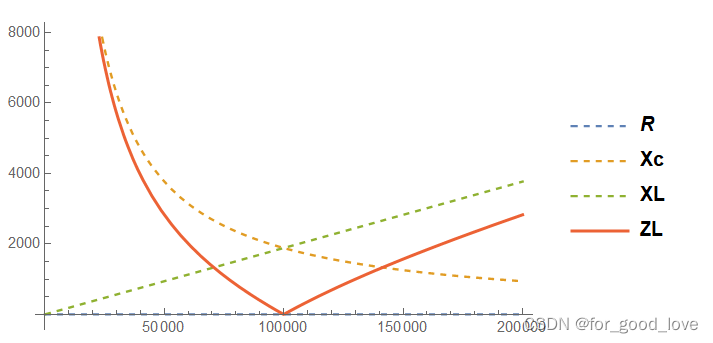
$\qquad$ 很容易画出R，XL，Xc，ZL随着频率f变化的曲线图，从图中可以看出，当fs=fr时，ZL有最小值（但这里仍需注意是正弦电源激励下），那么对应此时电流有最大值。定义品质因数 $Q=\frac{w_oL}{R}=\frac{1}{w_ocR}=\frac{1}{R}=\frac{L}{c}$ ，那么此时电容和电感上的电压数值 $U_L=U_c=QUs$ ，通常Q值很大，这意味着电感和电容的耐压要选取得非常高。
$\qquad$ 定义 $\eta=\frac{w}{w_o}$ ，即任意频率与谐振频率的比值。计算从输入电压到输出电流的传递函数，其实就是阻抗之和 $H(s)=\frac{I_o(s)}{U_i(s)}=\frac{1}{R+sL+1/sc}$ ,s=jw带入有： $H(jw)=\frac{1}{R+j(wL-1/wc)}\qquad H(j\eta)=\frac{1}{R\left[1+jQ(\eta-\frac{1}{\eta})\right]}$
容易得出： $Arg\left(H(j\eta)\right)=-\frac{1}{R}\quad arctan \left[Q(\eta-\frac{1}{\eta})\right]$
$Am(H(j\eta))=\left|\frac{1/R}{1+jQ(\eta-\frac{1}{\eta})}\right|=\left|\frac{1/R\left(1-jQ(\eta-\frac{1}{\eta})\right)}{1+Q^2(\eta-\frac{1}{\eta})^2}\right|=\frac{1/R}{1+Q^2(\eta-\frac{1}{\eta})^2}$
或者有一种更简洁的表达。注意到 $x)=\frac{1}{\sqrt{1+x^2}}$ ，带入有： $Am(H(j\eta))=cos(Arg[H(j\eta)])$

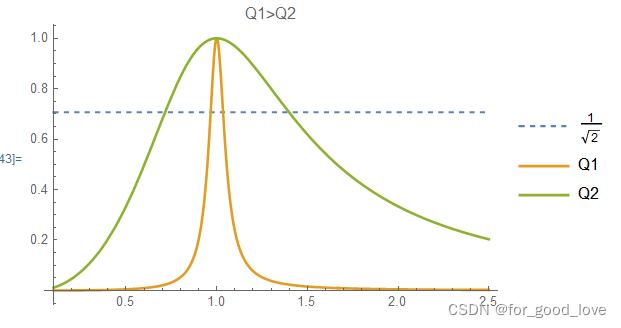
在这里插入图片描述

$\qquad$ 画出不同Q值下的幅频特性曲线如上图；显然可以看出：1、他们都在谐振点 $\eta=1$ 处出现峰值，且在其领域 $\eta=1+\Delta\eta$ 内都有较大幅度的输出信号。这说明LC串联电路选择不同的频率时，会得到不同频率的信号，而R只会影响通频带；**2、**电路在全频域内都有输出，但只有在谐振点附近的较小的领域 $\eta=1+\Delta\eta$ 内有较大的幅值；这就表明，LC滤波是不可能完全滤掉非基波频率，而且Q值越大，图像越“尖”，即通频带越小。理论下，当 $Q->\infty$ 时，可以完全滤掉其他谐波，但显然这是不可能的，想想前面说的谐振时电容和电感上的电压数值 $U_L=U_c=QUs$ 。

方波的傅里叶分解

$\qquad$ 任何周期信号都可以分解为三角函数所构成的级数之和。显然，此时的方波电源输出是奇函数，那么就没有常数项和偶次谐波。
$U_o=\left\{ \begin{aligned}Vdc & \qquad(0<t<\frac{1}{2T})\\-Vdc&\qquad(\frac{1}{2T}<t<\frac{1}{T}) \end{aligned}\right.$
傅里叶分解后是：
$\begin{aligned}U_o = &\frac{4Vdc}{\pi}\left(sin\ wt+\frac{1}{3}sin\ 3wt+\frac{1}{7}sin\ 7wt+\cdots\right)\\ = &\frac{4Vdc}{\pi}\sum_{k=1}^{n}\frac{1}{2k+1}sin\ (2k+1)wt \end{aligned}$
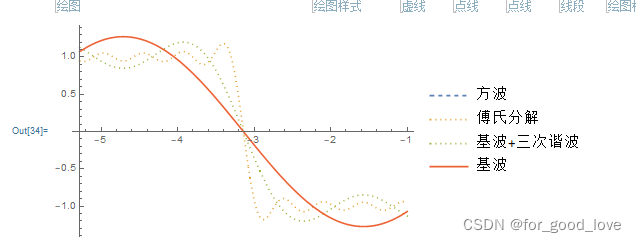
在这里插入图片描述
$\qquad$ 在mathematical下将方波分解，很明显看出，三次谐波对基波影响最大，从数学表达上看也是显然的，因为其幅值是基波的1/3
$\qquad$ 结合上面的看，当带宽选取在基波到三次谐波附近时，可以对三次谐波进行滤波，但滤波的本质是衰减（明白了这个就知道为什么LC参数都必须是功率器件参数），若Q值选取较小时候根本达不到滤波效果，当Q值很大时，在保证滤掉三次谐波的同时可以做到尽量不衰减基波。
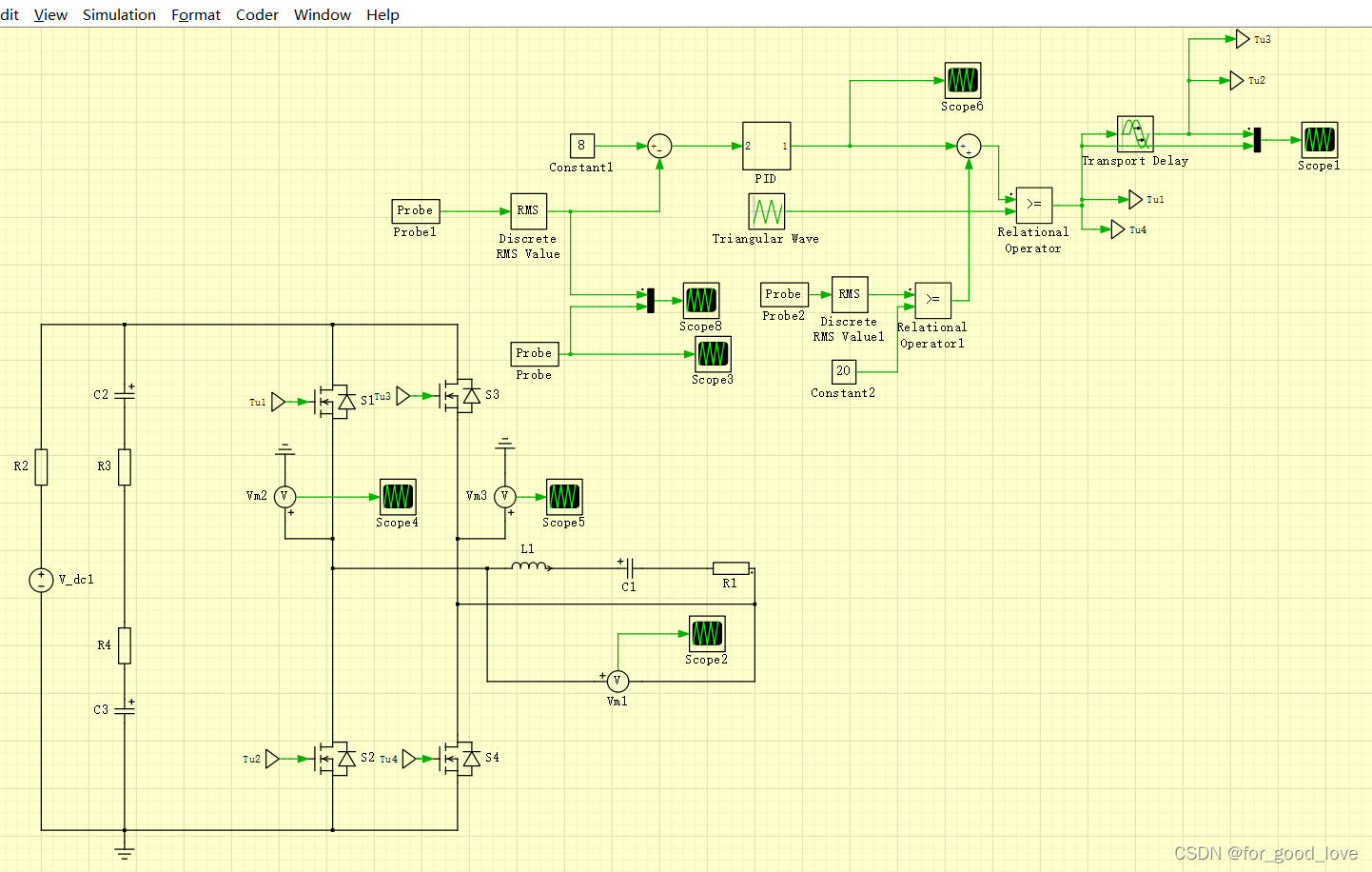
在这里插入图片描述
$\qquad$ 下面是去年年底画的BMS板子
### 三级目录