方波三角波THD理论计算值以及硬件实现电路
THD:谐波失真度
一般而言THD的计算在硬件实现方面,都是直接采集波形,然后在数字域中进行FFT,计算各谐波分量,但是通过计算各谐波分量的问题是,可能忽略掉了高次谐波的影响,导致实际测量偏小。
这里采用计算有效值来实现THD的计算,计算公式如下:
T
H
D
=
E
2
?
U
1
2
U
1
THD = \frac{\sqrt{E^2-U_1^2}}{U_1}
THD=U1?E2?U12???
其中
E
E
E为方波或者三角波的有效值,
U
1
U_1
U1?为方波或三角波基次谐波的有效值
文章目录
理论计算
方 波 T H D = 48.3 % 方波THD=48.3\% 方波THD=48.3%
对于一个峰峰值2Vpp的方波而言,其峰值为1V,方波图如下图所示
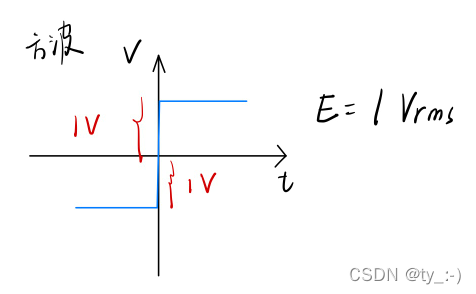
对于该方波而言 E = 1 V r m s E=1V_{rms} E=1Vrms?
对于这个方波而言,其傅里叶级数展开为(这里只看基波):
4
π
V
\frac{4}{\pi}V
π4?V,注意该值是基波的峰值(峰峰值的一半),考虑到基波为正弦波,所以我们就可以得到,对于该方波而言
U
1
=
4
π
2
=
2
2
π
V
r
m
s
U_1=\frac{4}{\pi\sqrt{2}}=\frac{2\sqrt{2}}{\pi}Vrms
U1?=π2?4?=π22??Vrms
代入THD的公式:
T
H
D
=
E
2
?
U
1
2
U
1
=
1
2
?
(
2
2
π
)
2
2
2
π
≈
48.3
%
THD = \frac{\sqrt{E^2-U_1^2}}{U_1} = \frac{\sqrt{1^2-{(\frac{2\sqrt{2}}{\pi})}^2}}{\frac{2\sqrt{2}}{\pi}}\approx48.3\%
THD=U1?E2?U12???=π22??12?(π22??)2??≈48.3%
三 角 波 T H D = 12.1 % 三角波THD=12.1\% 三角波THD=12.1%
对于一个峰峰值2Vpp的三角波而言,其峰值为1V,三角波图如下图所示
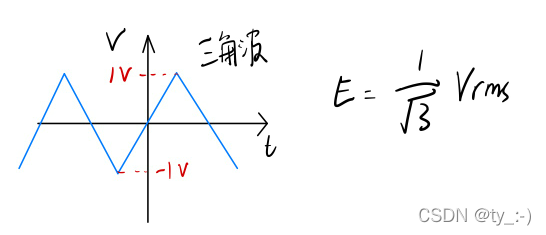
对于该三角波而言 E = 1 3 V r m s E=\frac{1}{\sqrt{3}}V_{rms} E=3?1?Vrms?,具体计算公式需要用到积分方程,根据有效值的定义可以得到
对于这个三角波而言,其傅里叶级数展开为(只看基波):
8
π
2
V
\frac{8}{{\pi}^2}V
π28?V,这里也是峰值(峰峰值的一半),考虑到基波为正弦波,所以可以得到,对这个三角波而言:
U
1
=
8
π
2
2
=
4
2
π
2
V
r
m
s
U_1=\frac{8}{\pi^2\sqrt{2}}=\frac{4\sqrt{2}}{\pi^2}V_{rms}
U1?=π22?8?=π242??Vrms?
代入THD的公式:
T
H
D
=
E
2
?
U
1
2
U
1
=
1
3
?
32
π
4
4
2
π
2
≈
12.1
%
THD = \frac{\sqrt{E^2-U_1^2}}{U_1} = \frac{\sqrt{\frac{1}{3}-\frac{32}{\pi^4}}}{\frac{4\sqrt{2}}{\pi^2}}\approx12.1\%
THD=U1?E2?U12???=π242??31??π432???≈12.1%
注意三角波
对于三角波而言,上述波形的基波分量正如计算;但是另一种形式的三角波,全为正的情况下,它的傅里叶级数并不是这个。这一点在郑君里的信号与系统中有说明
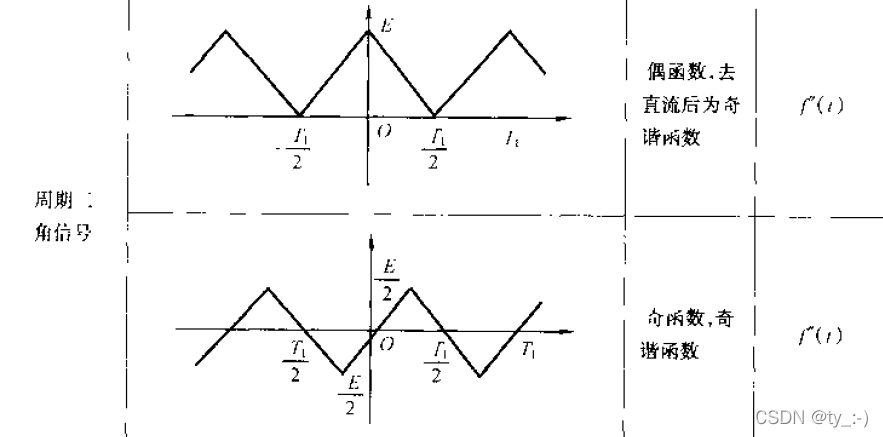
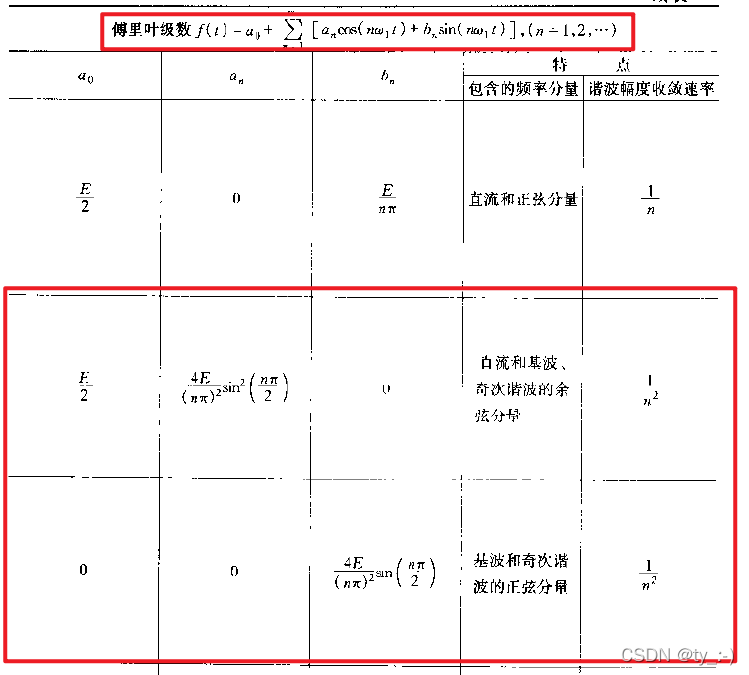
硬件实现电路
为了验证理论值和实际计算一致,这里搭建了一个简单的硬件电路。用到的芯片有AD637(有效值计算),OPA2277(进行滤波,滤除高次谐波),流程图如下
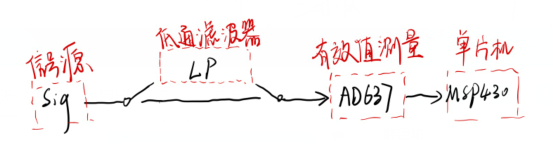
低通滤波器使用OPA2277搭建了一个8阶的巴特沃斯低通滤波器;
AD637负责把信号的有效值转换成直流量,送给单片机;
单片机通过片内AD采集直流信号,同时控制继电器信号的通路情况,计算结果并显示到屏幕上。
方波结果如下:存在一定的误差,但是在误差允许范围内。

三角波结果如下:存在一定的误差,但是在误差允许范围内。
