1. 同步时钟
时钟同源可称为同步时钟,不过时钟频率相同、相位差固定,以及时钟频率比为整数倍的时钟也可称为同步时钟,其重点在于对于每个发起时钟沿,其捕获时钟沿 都是确定且合理的
● 同源时钟:时钟产生的源头相同,例如PLL,相位不需要相同,只要求相位固定。
1.1. 同源同频
说明两个时钟的相位差是常数
同相位
不解释
不同相位
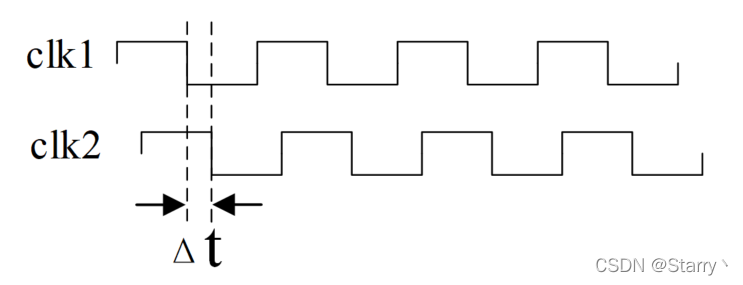
我们从公式去分析,STA中只有建立时间检查与时钟有关,而对于同频不同相位的时钟而言,公式变成
T s e t u p U F F 1 < T △ p h a s e + T c l k 2 U F F 1 ? ( T c l k 2 U F F 0 + T C K 2 Q U F F 0 + T U F F 02 U F F 1 ) (a) T^{UFF1}_{setup}<T_{△phase}+T_{clk2UFF1}-(T_{clk2UFF0}+T^{UFF0}_{CK2Q}+T_{UFF02UFF1}) \tag{a} TsetupUFF1?<T△phase?+Tclk2UFF1??(Tclk2UFF0?+TCK2QUFF0?+TUFF02UFF1?)(a)
( a ) (a) (a)式中的相位偏差 T △ p h a s e T_{△phase} T△phase?替换了原来的时钟周期 T c l k T_{clk} Tclk?。
注意一定有 T △ p h a s e < T c l k T_{△phase}<T_{clk} T△phase?<Tclk?成立,距离发起沿最近的时钟沿才是捕获沿。
在这种情况下, ( a ) (a) (a)式依旧可以满足,不过有了一些变化
● T △ p h a s e T_{△phase} T△phase?不能过小,否则亚稳态
一般来说时钟周期 T c l k T_{clk} Tclk?比建立时间 T s e t u p U F F 1 T^{UFF1}_{setup} TsetupUFF1?还是大很多的,但是这里的相位差 T △ p h a s e T_{△phase} T△phase?可就不一定了,谁知道大多少呢?
● 组合逻辑 T U F F 02 U F F 1 T_{UFF02UFF1} TUFF02UFF1?要求更严格了, 即能取到的最大值更小了
相比于同源同频同相,同源同频不同相的 ( a ) (a) (a)式右侧被减数变小了,又因为是同源 T c l k 2 U F F 1 ? T c l k 2 U F F 0 ? T C K 2 Q U F F 0 T_{clk2UFF1}-T_{clk2UFF0}-T^{UFF0}_{CK2Q} Tclk2UFF1??Tclk2UFF0??TCK2QUFF0?没变化,所以要想继续满足该不等关系,减数能取到的最大值变小了。
注意,此处说的是产生时钟的这个时钟源是同频固定相位差的,不是时钟偏斜导致沿到达各触发器CK端的时间存在相位差
