[嵌入式]Simulink永磁同步电机控制仿真系列九：严谨的foc时序及细节思考

一、引言

之前写过foc通俗讲义，讲foc控制的原理以及其优势，但是并没有深入去分析其时序，也没有分析其具体实现，今天写一篇时序相关的文章，具体分析foc流程，并思考其中一些细节之处的设计。为了便于讲解，我使用simulink搭建了一个模型，使用matlab function从实现一个pwm定时器开始，实现了svpwm调制，坐标变换，等。使用matlab function编写模块，作为模板共享，更方便其他用户的改造，也便于不熟悉simulink的小伙伴理解。除了基础的foc框架外，还考虑了时序相关处理，采样及foc计算全部使用定时器触发，同单片机控制时序一致。除此之外还实现了环路参数自动计算，所有变量使用国际标准单位。

二、设计触发器

考虑单片机foc时序，foc相关算法在电流采样中断中执行，每个pwm周期触发一次(双采样双更新方案触发两次)，电流采样设计为一个采样序列，转换开始命令到达后，按序列顺序开始转换，完成整个序列转换后触发电流采样完成中断。为了尽可能减小pwm开关引入的电流纹波，每次电流采样都在定时器计数到固定值时，并处于零矢量中点时进行。
为尽可能接近单片机foc时序，设计一个定时器，下图中上方黄色通道为上桥控制信号，蓝色为下桥控制信号，中间为计数器，计数器使用中间对齐模式，计数值小于比较值时上桥打开，计数值大于比较值时下桥打开，最下面为触发信号，在计数器最大值处有效。对应单片机中adc采样完成信号。

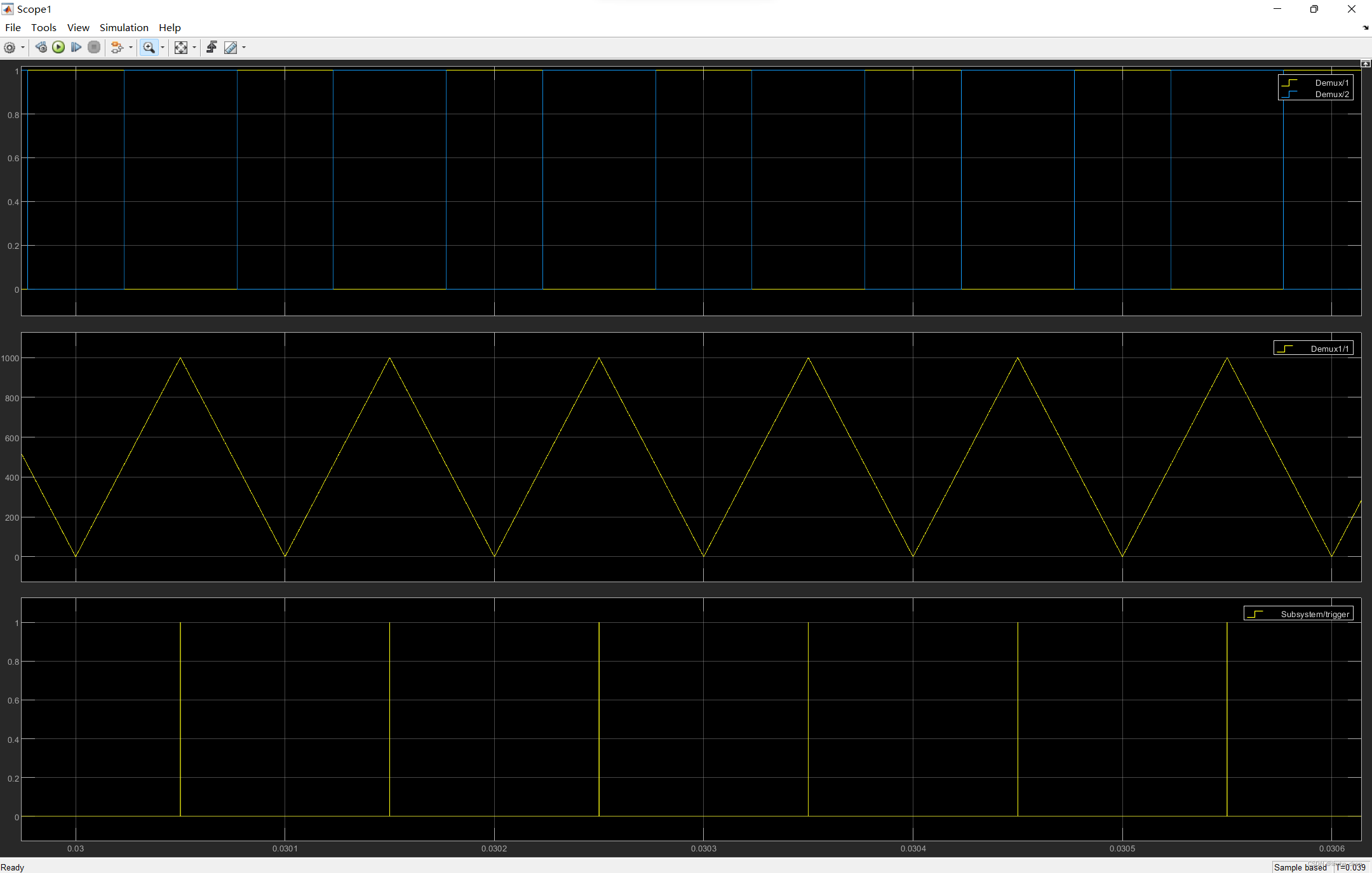
定时器运行主频为20M，设置定时器计数最大值1000，foc触发信号频率为10K；
按上述时序采样，结果如下图。其中黄色波形为原始电流波形(10Mhz采样)，蓝色波形为foc采样电流(10Khz采样)，容易看出，foc环路计算的电流有效去除了开关管开关电感充放电引入的电流纹波。

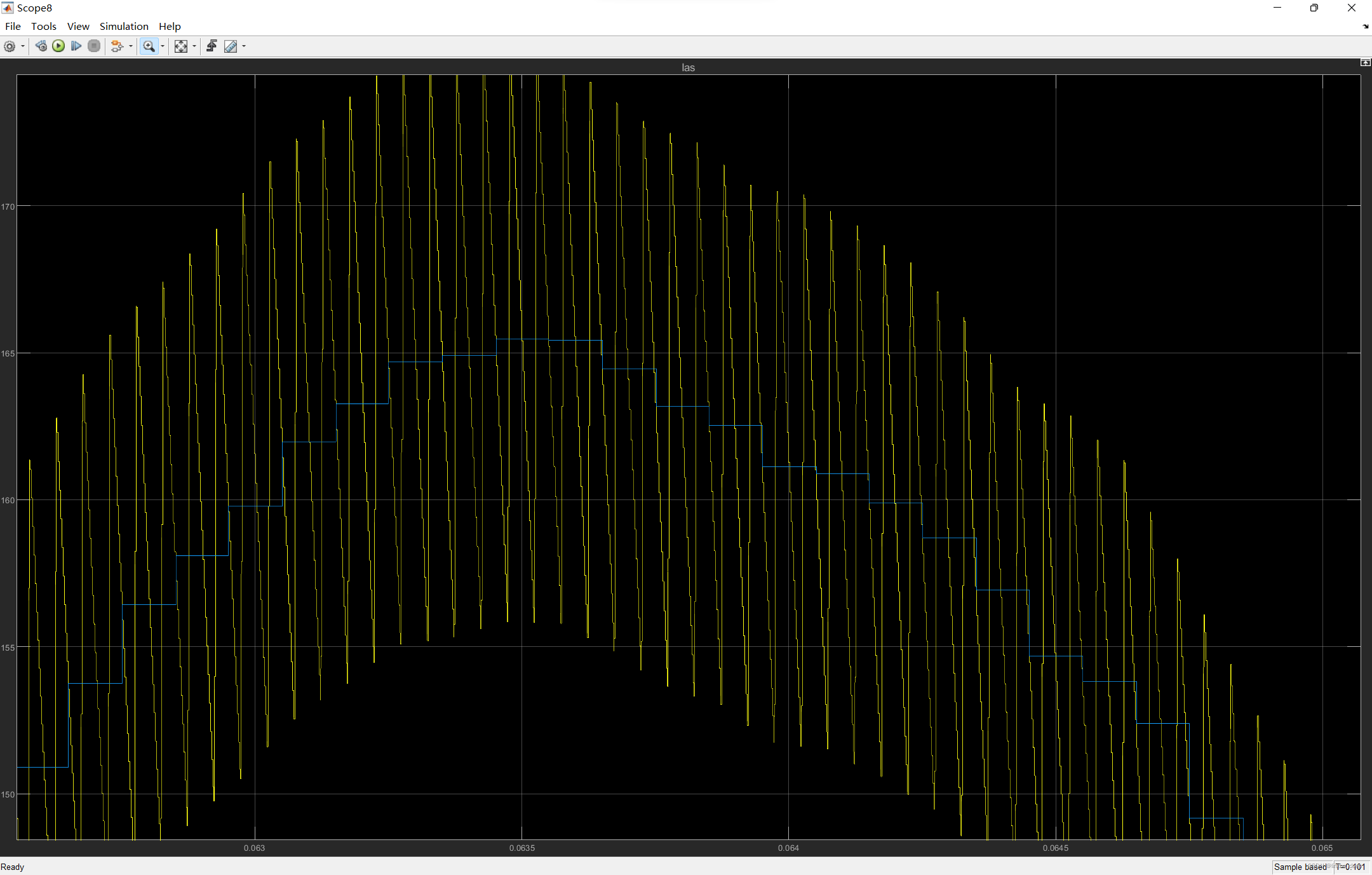
三、foc建模

完成了定时器触发，得到了电流信号，下一步实现foc子模块。

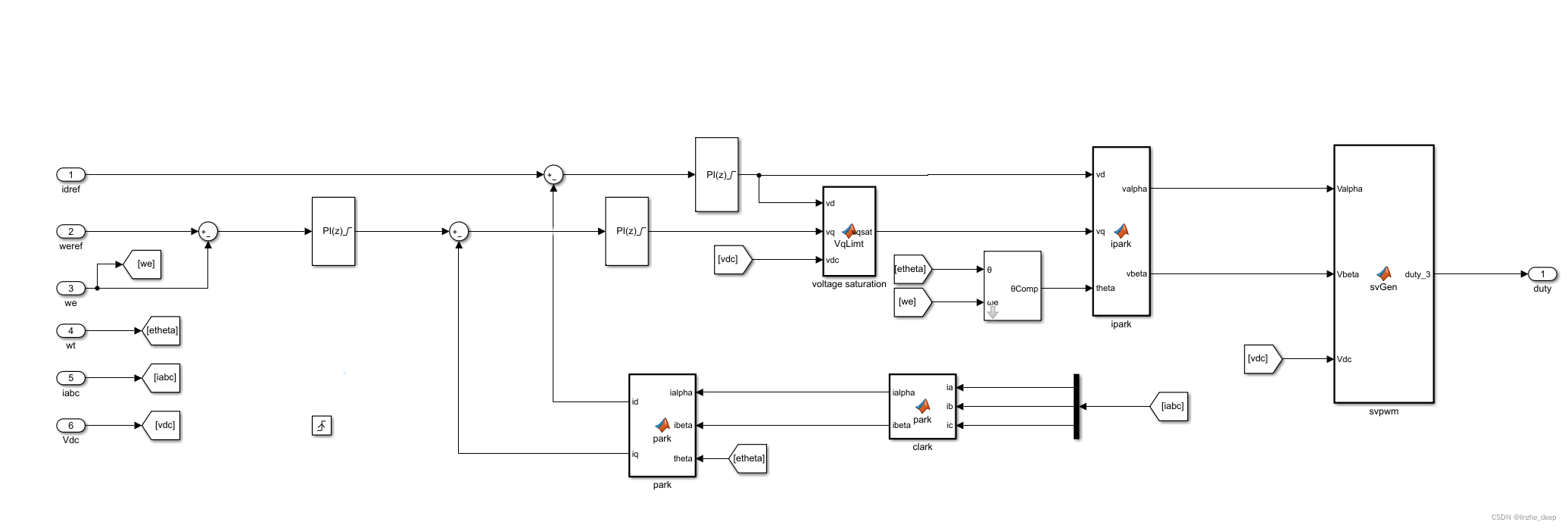
foc模块输入：id参考电流，参考速度，反馈速度，反馈角度，采样电流，采样母线电压。
foc模块输出：三相给定电压。

3.1 控制所需信号采样

模块在触发信号上升沿到来时运行，触发信号到来后，使用当前采样值进行电流clark变换，park变换，模型中所有坐标变换均为等幅值变换。需要注意的是，此时的电流采样值是当前时刻的电流，此时的角度为当前时刻的角度。而电机转子当前的角度，是上一次foc计算得到的电压作用到电机定子的结果，这一点细节非常重要，稍后还会再说到。

3.2 控制环路设计

到了这里我们已经得到了dq轴电流，id，iq；我们知道iq电流和电磁扭矩正相关，对于无凸极性的同步电机，id = 0的控制策略即最高效率策略。所以我们构建pi调节器，使id = 0；q轴电流给定值iqref由速度环pi得到，当反馈速度小于给定速度时，增大转矩，即增大iqref，反之，当反馈速度大于给定速度时，减小转矩，即减小iqref；得到iqref后和q轴电流反馈iq构建pi调节器，控制目标为iq = iqref；对于无凸极性的电机Ld = Lq，DQ轴电流环模型一致，使用同样的电流环参数，具体电流环参数设置留到下文分析。
我们知道对于物理世界的电机，要受到物理限制，它的输入电流没办法无限大，受供电电源限制，输入到电机的电压也不可能无限大，那控制器设计时就要注意这一点。对于某个特定的电机，电机的最大允许工作电流已知，即要保证驱动器输出最大电流（此处讲到的电流均值相电流幅值）小于Imax，为此，有sqrt(IdId + IqIq) < Imax;因为控制目标为id = 0；所以，为满足上式，只需Iq < Imax，为了使Iq < Imax,需要Iqref < Imax；这是速度环限幅原则；电流环的输出是电压，驱动器能够输出的最大电压受母线电压决定。笔者svpwm原理分析那篇文章中说过，驱动器能够输出的最大线电压的幅值等于母线电压，所以最大相电压幅值Vs = Vdc/sqrt(3)；对于等幅值变换，sqrt(VdVd + VqVq) = sqrt(ValphaValpha + VbetaVbeta) = Vs;所以为了保证输出电压不超过母线电压能够支持的最大值，要保证Vd，Vq在安全范围内；其中Vd为耦合电压，和转速转速转矩的乘积正相关，对Vd限幅会导致耦合电压产生id电流，降低电机运行效率，所以我们通常较少限制Vd，仅令Vd <= Vdc/sqrt(3);只要逆变器能够输出，就让Vd输出，以保证id能被控制到参考值。但是当Vd！=0时，Vq便没办法达到Vdc/sqrt(3);Vq能够达到的最大值是Vqmax = sqrt(Vdc/sqrt(3)Vdc/sqrt(3) - VdVd);所以，限幅Vq到Vqmax.

3.3 输出电压

通过环路得到Vd，Vq后，进行ipark变换，得到Valpha，Vbeta，需要考虑的是，输出的电压不会立即作用到电机上，我们输出的pwm波要一个完整的周期结束，高电平时间与低电平时间平均下来才是我们要输出的有效电压。所以实际上我们的电压输出到作用到电机有一个pwm周期的滞后，而这个过程中，电机仍然在惯量作用下运行。所以为了保证矢量角更准确，ipark使用的角度应该是预测的一个pwm周期后的角度，此为角度补偿。
得到valpha，vbeta后，使用svpwm得到三相占空比。仿真中，valpha,vbeta单位为V，到svpwm模块转换为占空比，范围为0-1，转换需要参考母线电压，仿真中把母线电压引入到svpwm模块。

四、环路参数的计算

我们常说，foc坐标变换的目的是把交流电机等效为直流电机去控制，我们对同步机dq坐标系模型进行等效处理如下

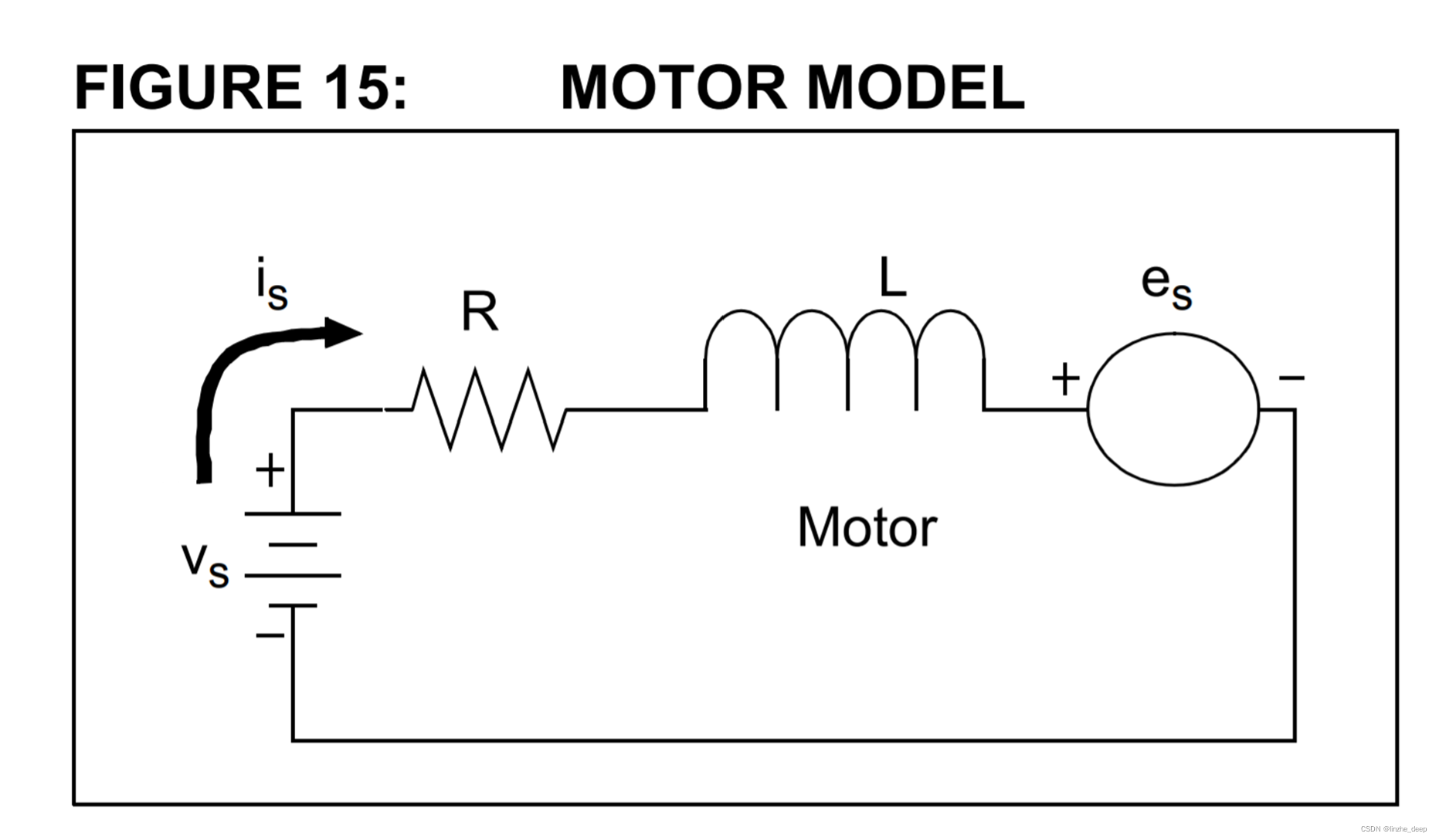
其中R为等效电阻Rs，L为等效电感Ls，es为反电动势及耦合电压，Vs为Vd或Vq电压。
如果我们仅看加到电阻及电感上的电压。
其传递函数：
$$sys=\frac{I}{V}=\frac{1}{R+sL}=\frac{1/R}{1+\tau s}$$
PI控制器传递函数：
$$sys=\frac{V}{I_{err}}=P(1+I\frac{1}{s})=P(\frac{s+I}{s})$$
把PI控制器加入到电机模型：
$$\frac{I}{I_{err}}=\frac{1}{R+sL}?P(\frac{s+I}{s})=\frac{sP+IP}{sR+s^{2}L}$$
$$令P={\omega }_{c}L，I=\frac{R}{L}$$
可以抵消一个极点，对于不同的电机，消除不同电机参数的影响，使系统响应仅由\omega_c 决定
$$\frac{I}{I_{err}}=\frac{s{\omega }_{c}L+{\omega }_{c}R}{sR+s^{2}L}=\frac{{\omega }_c}{s}$$
根据上述结论，建立仿真模型，图中上方模型为电机模型和pi控制器的串联，PI参数按照上述设置原则设置，下方模型为系统等效模型，可以看到，模型的特性和电机参数无关，运行仿真，两个模型得到的仿真结果完全一致。

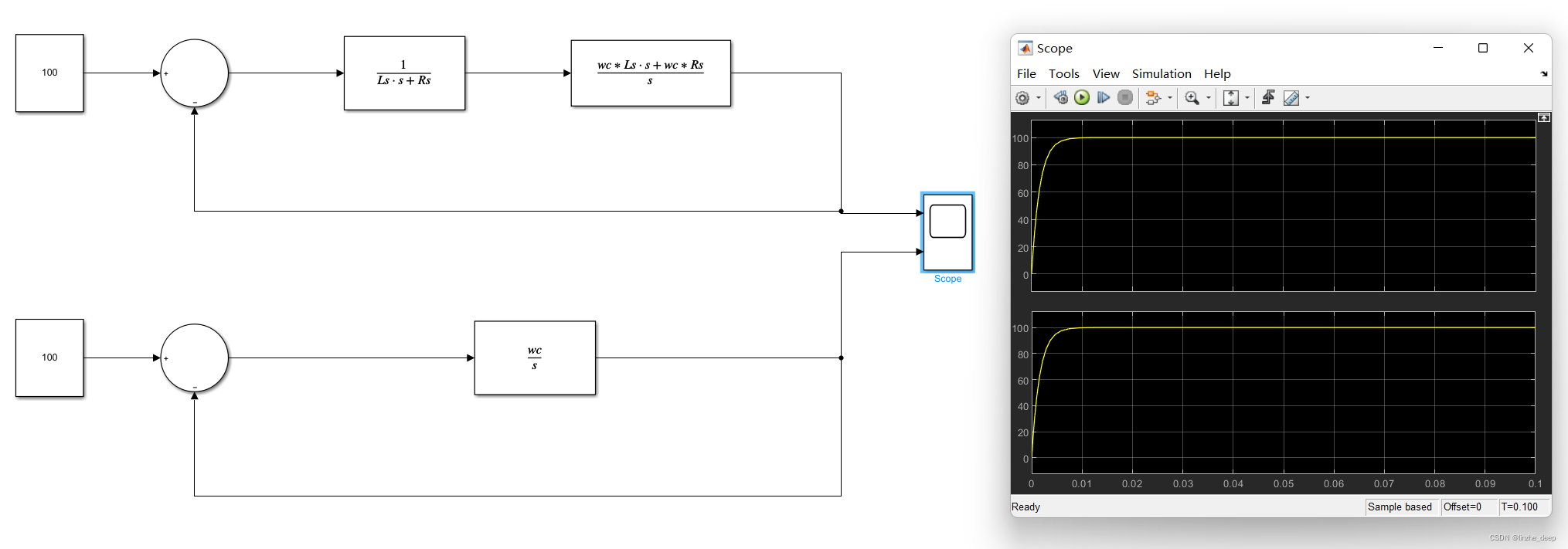
需要注意的是上述分析忽略了反电势和耦合电压，实际电路中，这两部分占比较大不可忽略，需要通过前馈把这两项的影响抵消。
模型下载链接：[https://download.csdn.net/download/linzhe_deep/85336081]

2022深度学习开发者峰会

5月20日13:00让我们相聚云端，共襄盛会！