[嵌入式] 电容并联放电电阻的RC 电路时间常数计算，一阶线性常系数微分方程

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 嵌入式 -> 电容并联放电电阻的RC 电路时间常数计算，一阶线性常系数微分方程 -> 正文阅读

[嵌入式]电容并联放电电阻的RC 电路时间常数计算，一阶线性常系数微分方程

就是在谁都知道的RC 电路里的电容旁边并联一个放电电阻，计算它对时间常数的影响，参考下面的示意图：

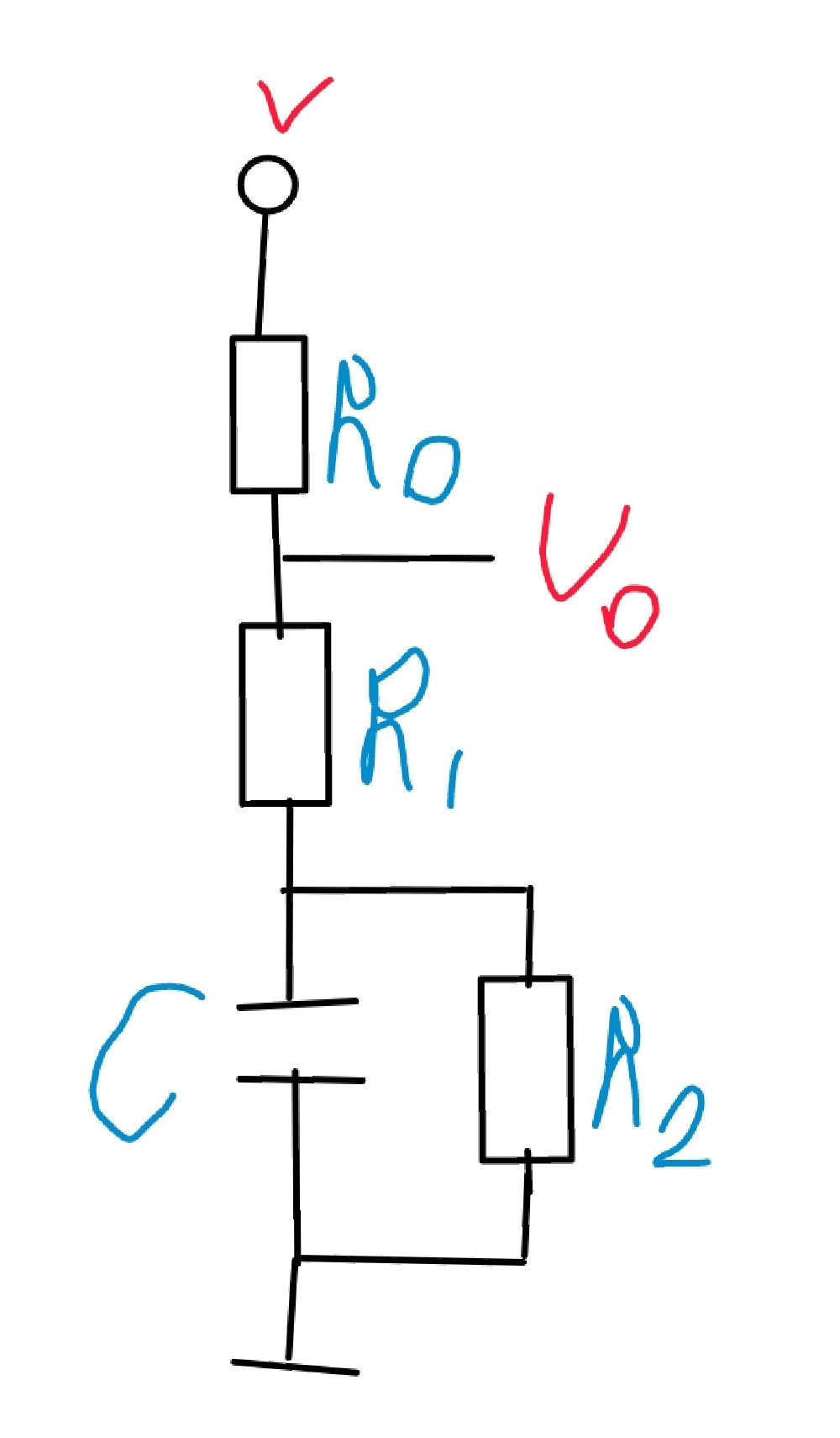
在这里插入图片描述

电路的输入电压是电源电压V，在R0 和R1 之间连接着一个单片机引脚，所以想计算上电后单片机引脚上电压的变化，也就是输出电压Uo。电容C 通过R0 和R1 充电，R2 放电。

计算

以前电路上好像学了简化方法，叫三要素法，但是我忘光了，所以就从基础开始算。

电容两端的电压公式如下：

${U_c}' = \frac{1}{C} I_c \tag{1}$

即电压对时间的导数和电容量C 成反比，和电流正比。设，经过电容的电流是 $I_c$ ，经过R2 的电流是 $I_2$ ，干路电流 $I_1$ 是两支路之和。因为R2 两端电压和电容电压相等，则：

$I_2 = \frac{U_c}{R_2} \tag{2}$

作用在干路电阻R0 + R1 上的电压又是输入电压V 和电容电压 $U_c$ 之差，于是干路电流就是：

$I_1 = \frac{V - U_c}{R_0 + R_1} \tag{3}$

电容电压就可以表示成：

$\begin{aligned} {U_c}' &= \frac{1}{C} ( I_1 - I_2) \\ &= \frac{1}{C} (\frac{V - U_c}{R_0 + R_1} - \frac{U_c}{R_2}) \end{aligned} \tag{4}$

微分方程的感觉已经有了? 整理一下，变成标准的一阶线性微分方程的形式：

${U_c}' + KU_c = D \tag{5}$

其中，

$\begin{aligned} \begin{cases} K &= \frac{R_0 + R_1 + R_2}{C R_2 (R_0 + R_1)} \\ D &= \frac{V}{C (R_0 + R_1)} \end{cases} \end{aligned} \tag{6}$

可见K 和D 都是和时间无关的常数。高数里讲过，这种微分方程是比较简单的，有标准的解法。

解方程和时间常数

其实这一步已经能看出时间常数是什么了，和标准的一阶系统微分方程比较一下，能看出时间常数就是K 的倒数，电容量C 在分子上，C 越大时间常数越大，也符合常识。不过还是激情的解一遍方程吧。

按照标准方法，首先把方程两边同时处理一下：

$e^{Kt}({U_c}' + K U_c) = e^{Kt}D \tag{7}$

此时方程左边可以逆用导数乘法公式，变成：

$(e^{Kt} \cdot U_c)' = e^{Kt} D \tag{8}$

然后就是两边积分，

$\begin{aligned} ( e^{Kt} U_c ) \vert_0^t &= D \int_0^t e^{Kt} dt \\ &= \frac{D}{K} e^{Kt} \vert_0^t \\ e^{Kt} U_c(t) - U_c(0) &= \frac{D}{K}(e^{Kt} - 1) \end{aligned} \tag{9}$

初始状态电容电压设为0，所以 $U_c(0) = 0$ ，则上式变为：

$\begin{aligned} e^{Kt} U_c(t) &= \frac{D}{K} \cdot (e^{Kt} - 1) \\ U_c(t) &= \frac{D}{K} \cdot (1 - e^{-Kt}) \\ &= \frac{D}{K} \cdot (1 - e^{\frac{-t}{K^{-1}}}) \end{aligned} \tag{10}$

标准的一阶系统阶跃响应是：

$e^{\frac{-t}{T}} \tag{11}$

所以时间常数T 就是 $K^{-1}$ ，也就是K 的倒数，观察一下K 倒数的形式：

$\begin{aligned} K^{-1} = T &= \frac{C R_2 (R_0 + R_1)}{R_0 + R_1 + R_2} \\ &= C[R_2 \parallel (R_0 + R_1)] \end{aligned} \tag{12}$

发现时间常数是C 乘上R2和（R0 + R1）的并联。而式10 前面的系数 $\frac{D}{K}$ 是：

$\frac{D}{K} = \frac{R_2 V}{R_0 + R_1 + R_2} \tag{13}$

也就是R2 和（R0 + R1）的串联分压。

结果

这下就可以考虑输出电压Uo 了，Uo 是电容电压加上R1 的压降：

$\begin{aligned} U_o &= U_c(t) + I_1 R_1 \\ &= U_c(t) + \frac{[V - U_c(t)] R_1}{R_0 + R_1} \\ &= \frac{R_0}{R_0 + R_1} \cdot U_c(t) + \frac{R_1 V}{R_0 + R_1} \end{aligned} \tag{14}$

可见，输出电压Uo 包含一个常数项，就是电源电压V 经过R0 和R1 的分压。也很好理解，在初始状态电容电压为0，就相当于V 经过R0 和R1 接地。

现在回到实际，假设输入电压V = 5V，芯片引脚输入高电平阈值是4V，要计算输出电压上升到4V 的所需时间。假设输出电压初始值低于4V，设那个常数项电压是 $U_r$ ，也就是要算 $U_c(t)$ 上升到4V － $U_r$ 的时间。

$\begin{aligned} U_c(t) &= 4 - U_r \\ \frac{R_2 R_0 V}{(R_0 + R_1 + R_2)(R_0 + R_1)} \cdot (1 - \exp(\frac{-t}{C[R_2 \parallel (R_0 + R_1)]})) &= 4 - \frac{R_1 V}{R_0 + R_1} \end{aligned} \tag{15}$

这个方程，emmm，头皮发麻[doge]，不过忽略那些常数的话结构也不复杂。代换整理一下：

$e^{\frac{-t}{T}}) = U_d \tag{16}$

解得：

$\ln(1 - \frac{U_d}{A}) \tag{17}$

再看一眼参数A 和T，令串联电阻 $R_s = R_0 + R_1$ ，当放电电阻R2 很大时：

$C[R_2 \parallel R_s] \approx C R_s \tag{18}$

也就是当R2 很大时，时间常数主要和串联电阻有关。然后把A 分解回左右两部分：

$\begin{aligned} A = \frac{R_2}{R_2 + R_s} \cdot \frac{R_0 V}{R_s} &\approx (1 - \frac{R_1}{R_s}) V \\ &= (1 - q)V \end{aligned} \tag{19}$

当R2 很大时，左侧因子约等于1，右边因子再换一下形式，把R1 和Rs 的比值记为q，0 < q < 1。于是式17 的解可以写成：

$\begin{aligned} t &= -C R_s \ln(1 - \frac{4 - qV}{V - qV}) \\ &= -C R_s \ln(\frac{V - 4}{V(1 - q)}) \\ &= -C R_s \ln(\frac{1}{5(1 - q)}) \\ &= C R_s \ln(5(1 - q)) \end{aligned} \tag{20}$