提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
一、从excel导入数据
import matplotlib.pyplot as plt#画图
import numpy as np
import matplotlib
import xlrd #读excel数据用
file_location = "D:\\2010A\\01.xls"#文件路径
data = xlrd.open_workbook(file_location)#获取数据
#选择读取sheet,索引0是sheet1
sheet1 = data.sheet_by_index(0)
sheet2 = data.sheet_by_index(1)读数据用sheet.cell_value()
读最左上角的数据[0][0],和c语言的二维数组很相似
print(sheet1.cell_value(0,0))
print(sheet1.nrows)#返回行数目
print(sheet1.ncols)#返回列数目将某一列/行存入数组
data1 = [sheet1.cell_value(r,0) for r in range(1,sheet1.nrows)]#获取sheet1中第0列的数据
data2 = [sheet1.cell_value(0,r) for r in range(0,sheet1.ncols)]#获取sheet1中第0行的数据
#打印data2
for i in range(len(data2)):
print(data2[i])输出结果
?
?将第几列到第几列,第几行到第几行存入矩阵
data3 = [[sheet1.cell_value(r,c)for c in range(1,6)] for r in range(1,6)]二、最小二乘法多项式拟合
导入数据
sheet1_height = [sheet1.cell_value(r,3) for r in range(1,sheet1.nrows)]
sheet1_oil_intake = [sheet1.cell_value(r,2) for r in range(1,sheet1.nrows)]?导入拟合所需的包
import numpy as np
from scipy.optimize import leastsq
import pylab as pl拟合
#做最高次数为3的拟合
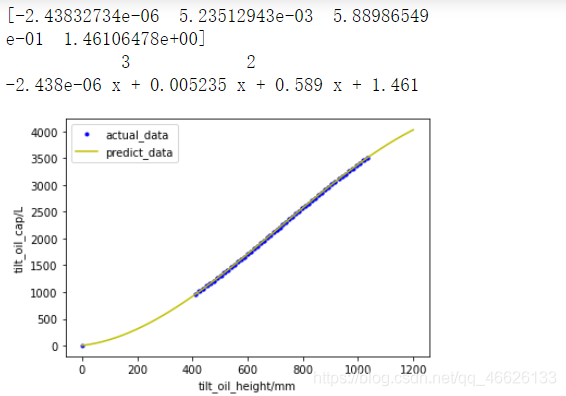
z1 = np.polyfit(sheet1_height,sheet1_oil_intake, 3)#生成多项式系数矩阵
p1 = np.poly1d(z1)# 生成多项式对象
print(z1)
print(p1)
# 横坐标x的范围
x = np.linspace(0,1200)
#纵坐标函数
y=p1(x)
plt.plot(sheet1_height,sheet1_oil_intake,'b.',x,y,'y-')#画实际数据散点图和拟合曲线
plt.legend(('actual_data','predict_data'), loc='upper left') #标示每条线的含义
plt.xlabel('tilt_oil_height/mm')#横坐标
plt.ylabel('tilt_oil_cap/L')#纵坐标
plt.savefig('D://2010A//Nochange.jpg')将图像保存?运行结果
三、最小二乘法拟合任意函数
导入包(使用curve_fit)
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit自定义函数
#自定义函数
def func(x, a, b,c):
return a*np.sqrt(x)*(b*np.square(x)+c)定义x,y数组
x = [20,30,40,50,60,70]
y = [453,482,503,508,498,479]
非线性最小二乘法拟合
curve_fit返回的是两个数组
popt,一维数组,残差最小时参数的值
pcov,二维阵列,popt的估计协方差。对角线提供参数估计的方差。
popt, pcov = curve_fit(func,x,y)
print(popt)运行结果
popt: [-1.96401671e-01 4.20401375e-02 -4.85953552e+02]带入参数值得到拟合函数
y = func(x,popt[0],popt[1],popt[c])