Webots中获取机器人质心三维速度的一种简单方法

0 前言

??最近实在是太忙了，有空把CLion和VSCode以及PyCharm配置Webots的文章写一下，我自己直接用的CLion配置的，能像VS一样直接在Webots外部运行extern控制器。
??Webots中常用的传感器有GPS获取机器人全局位置，加速度计（Accelerator）获取机器人全局加速度，磁力计（Gyro）获取刚体旋转角速度，IMU（Inertial Unit）获取机身欧拉角
??对于大多数Webots用户，主要工作还是开发控制算法，很多算法要求在仿真中能得到一些精确的机器人状态如质心速度等等，虽然在实际机器人开发中也是使用如上所列的多类传感器结合状态估计算法来获取这些状态，但为了提高控制算法开发速度，我这里给出一个简单的质心速度求取方法。这也是我看在pybullet中常用的一种方法。

1 旋转矩阵

??假设全局坐标系为 ${s}$ ，机身坐标系为 ${b}$ ，我们根据Webots中的IMU可以轻易求得从坐标系 $s$ 变换到坐标系 $b$ 旋转矩阵为 $R^b_s(t)$ ，具体怎么求马上讲，别急。
??求得旋转矩阵后，我们需要利用GPS做差分，得到机身速度在全局坐标系下的表示记为 $v_s$ ，同理机身速度在机身坐标系下的表示为 $v_b$ ，那么可以很轻易的得到他们的关系如下：
$v_s=R^b_s(t)v_b\tag{1}$
??亦即:
$v_b = R^b_s(t)^{-1}v_s=R^b_s(t)^{T}v_s\tag{2}$
??注意速度大小不随表示坐标系而改变，这是由旋转矩阵的性质决定的，保长度

1.1 Webots中旋转矩阵的求取

??首先我们看官方手册对IMU的描述：
Webots手册
??废话有点多，重点就是：

按手册所述配置好IMU坐标轴方向
IMU旋转顺序是YZX，即先绕X轴旋转，再绕Z轴旋转，最后绕Y轴旋转
??我们知道了旋转顺序就好说了，由于欧拉角是绕固定坐标系旋转，所以左乘，乘积如下：

$R^b_s=Rot(y,\beta)\cdot Rot(z, \gamma) \cdot Rot(x, \alpha)\tag{3}$

??其中 $\alpha$ 为横滚角roll， $\gamma$ 为俯仰角pitch， $\beta$ 为偏航角yaw。很容易根据旋转矩阵的公式求得：
$R^b_s=\begin{bmatrix} c_{\alpha}c_{\gamma} & -c_{\beta}c_{\alpha}s_{\gamma}+s_{\alpha}s_{\beta} & c_{\beta}s_{\alpha}s_{\gamma}+c_{\alpha}s_{\beta} \\ s_{\gamma} & c_{\gamma}c_{\alpha} & -c_{\gamma}s_{\alpha}\\ -s_{\beta}c_{\gamma} & s_{\beta}c_{\alpha}s_{\gamma}+s_{\alpha}s_{\beta} & -s_{\beta}s_{\alpha}s_{\gamma}+c_{\alpha}c_{\beta} \end{bmatrix}\tag{4}$
??其中 $s$ 代表 $s i n$ ， $c$ 代表 $c o s$ ，加个下标分别代表求对应角的正余弦值。有了这个东东后面就好办了，我弄了一个小车进行了测试，下面见代码。

2 代码展示

??小车IMU坐标系和全局坐标系如下图所示：

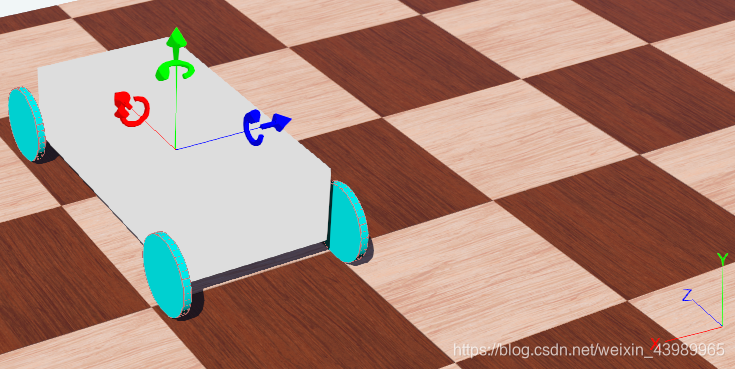
??我们可以测试我们刚刚求取的旋转矩阵是否正确，如下图所示：
在这里插入图片描述
??由此可见旋转矩阵求取正确，机身 $x$ 轴在全局坐标系下的表示为 $[0\quad 0 \quad 1]^T$ ，其他两轴也都正确。
??下面我们测试我们得到的机身坐标系下的速度和全局坐标系下的速度是否相同，相同岂不是我们白做工作了。利用坡道测试，当小车上坡时，全局坐标系下的 $y$ 方向和 $z$ 方向速度分量肯定不小，但机身坐标系下 $y$ 和z方向速度肯定很小。结果如下：
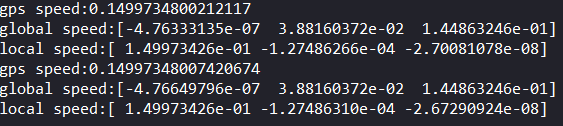
在这里插入图片描述

??其中由GPS求出的全局坐标系下速度的幅值为0.15左右，机身坐标系下的速度（local speed）只有x方向有较大速度，而全局坐标系下的速度表示在 $y$ 方向也有一个不可忽略的值。
??代码如下，实际上你可以对这个求GPS微分的过程进行一个滤波处理，我就懒得弄了，你也可以把小车悬空，测试小车下降速度，这里就不展示了，总的来说，我打算就用这个方法来估计机器人速度了，导航滤波机器人状态估计啥的也来不及去学去弄了。

2.1 代码说明与展示

??函数com_velocity_estimate()返回三个值，可以打印返回的旋转矩阵，看看IMU坐标轴在全局坐标轴的位置，是不是正确的以验证旋转矩阵求取的正确性，最后用求得的速度和GPS自带的一维速度获取函数进行比较，以及与直接微分求得的全局速度进行比较，发现误差还是不大的，希望大家能弄出更好的办法，到时候踢我一下，我直接用了，谢谢。

from controller import Robot
import numpy as np
import math
import copy

robot = Robot()
timeStep = int(robot.getBasicTimeStep())

motor = [robot.createMotor('LF'), robot.createMotor('RF'), robot.createMotor('RH'), robot.createMotor('LH')]

GPS = robot.createGPS("gps")
IMU = robot.createInertialUnit("IMU")

IMU.enable(timeStep)
GPS.enable(timeStep)

for i in range(4):
    motor[i].setPosition(float('+inf'))
    motor[i].setVelocity(-3)

pre_pos = np.array(GPS.getValues())


def com_velocity_estimate():
    global pre_pos

    euler = IMU.getRollPitchYaw()

    s_r = math.sin(euler[0])
    c_r = math.cos(euler[0])
    s_p = math.sin(euler[1])
    c_p = math.cos(euler[1])
    s_y = math.sin(euler[2])
    c_y = math.cos(euler[2])

    pos = np.array(GPS.getValues())

    velocity = (pos - pre_pos) / (0.001 * timeStep)

    pre_pos = copy.deepcopy(pos)
    rotate = np.zeros((3, 3), dtype=float)
    rotate[0, 0] = c_y * c_p
    rotate[0, 1] = s_r * s_y - c_y * c_r * s_p
    rotate[0, 2] = c_y * s_r * s_p + s_y * c_r
    rotate[1, 0] = s_p
    rotate[1, 1] = c_p * c_r
    rotate[1, 2] = -c_p * s_r
    rotate[2, 0] = -s_y * c_p
    rotate[2, 1] = c_r * s_y * s_p + s_r * c_y
    rotate[2, 2] = -s_y * s_r * s_p + c_r * c_y

    return rotate.T @ velocity, rotate, velocity


while robot.step(timeStep) != -1:
    # Read the sensors:
    # Enter here functions to read sensor data, like:
    #  val = ds.getValue()
    print("gps speed:{0}".format(GPS.getSpeed()))
    a, b, c = com_velocity_estimate()
    # print("gps_pos:{0},{1},{2}".format(gps_pos[0], gps_pos[1], gps_pos[2]))
    # print("acc:{0},{1},{2}".format(acc[0], acc[1], acc[2]))
    # print("euler:{0},{1},{2}".format(euler[0], euler[1], euler[2]))
    # print(b)
    print("global speed:{0}".format(c))
    print("local speed:{0}".format(a))