[开发工具]2021牛客多校5

比赛情况：


过程：一开始并没有签被签烂了的H题，cqf选择了首签K题，然后我切了H，再之后wmd开大毒瘤F题。然而到比赛结束F都未调出来。再之后我和cqf过了B期望，最后cqf过了一直被忽视的D。

TH Holding Two

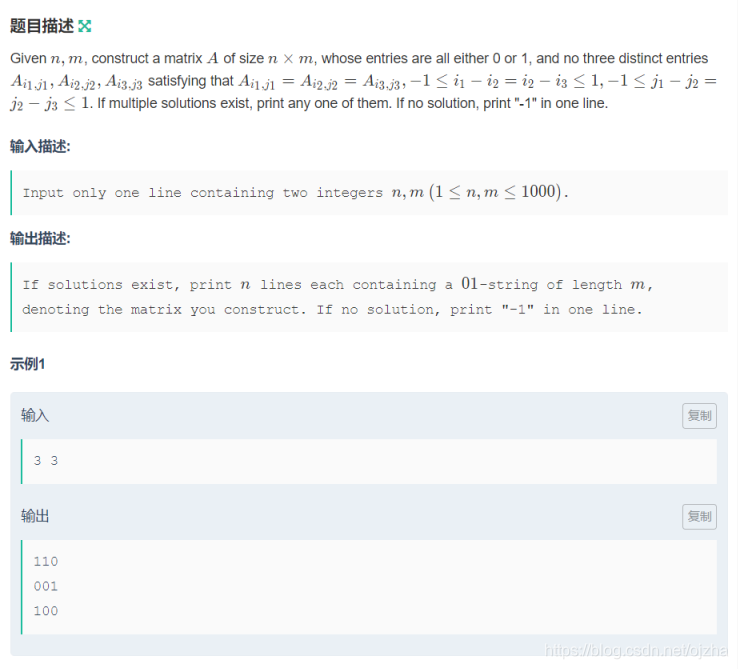
题意：构造一个$n?m$的矩阵，满足在一个$3?3$的矩阵中，每一行每一列每一条对角线都不会存在$3$个一样的数字。

idea：第一二行1010101010…
第三四行0101010101…
第五六又变回去1010101010…
循环就好

ACcode：

#include<bits/stdc++.h>
#define LL long long
using namespace std;

int n,m;
void solve()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		if( i%4==1 || i%4==2 )
		{
			for(int j=1;j<=m;j++)
			{
				printf("%d",j%2);
			}
			printf("\n");
		}
		else
		{
			for(int j=1;j<=m;j++)
			{
				printf("%d",(j%2) ^ 1);
			}
			printf("\n");
		}
	}
}

int main()
{
	solve();
	return 0;
}

TG Greater Integer, Better LCM

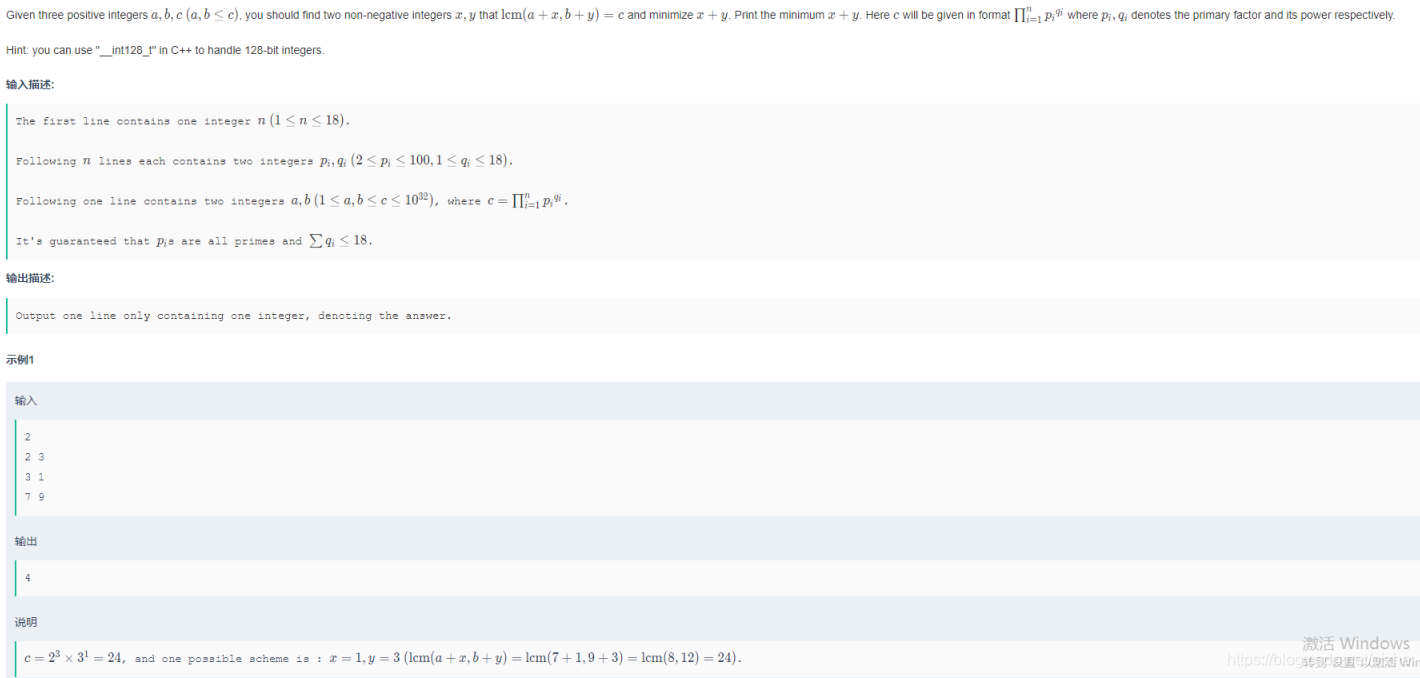
idea:首先很容易想到的是枚举哪些 pi 在 a+x 中取到 qi 的幂次，那么剩下的 pi 就得在 b+y 中取到 qi 的幂次，然后考虑 a+x 和 b+y 还都得是 c 的约数，所以问题就变成了：给定一个数字 x，找其大于等于一个数 y 且最小的约数。

一个暴力的做法是说，因为我们是有 x 的质因数分解的，那么就暴力枚举 x 的每个约数，和 y 做个比较然后取最优值即可，这样复杂度是 O(2n) 的，套上一开始的那层枚举复杂度则是 O(3n) 的，这大概率是会 TLE 的。但我猜总有能过的。

那么我们考虑优化上面那个做法，可以考虑用折半搜索来优化纯暴力枚举，这样复杂度就是 $O(n?2n/2)$ 的，套上一开始的那层枚举复杂度则是 O(n*(1+√2)n) 的，其中那个 n 是排序的复杂度，且本来常数就比较小，所以这个做法能有比较好的效果。

#include <cstdio>
#include <algorithm>
using namespace std;
int n;
int p[20],q[20];
char s[40];
__int128_t a,b,c;
__int128_t va[1<<18],vb[1<<18];
__int128_t ans;
char t[40];
int cnt;
void fd(__int128 v,int c,int bit)
{
	if (c>n)
	{
		if (v>=a)
			va[bit]=min(va[bit],v-a);
		if (v>=b)
			vb[bit]=min(vb[bit],v-b);
		return;
	}
	for (int i=0;i<=q[c];i++)
	{
		fd(v,c+1,bit|((i==q[c])<<(c-1)));
		v*=p[c];
	}
}
int main()
{
	scanf("%d",&n);
	c=1;
	for (int i=1;i<=n;i++)
	{
		scanf("%d%d",&p[i],&q[i]);
		for (int j=1;j<=q[i];j++)
			c*=p[i];
	}
	scanf("%s",s+1);
	for (int i=1;s[i];i++)
		a=a*10+s[i]-'0';
	scanf("%s",s+1);
	for (int i=1;s[i];i++)
		b=b*10+s[i]-'0';
	for (int i=0;i<(1<<n);i++)
		va[i]=vb[i]=c;
	fd(1,1,0);
	for (int i=2;i<=(1<<n);i<<=1)
		for (int j=0;j<(1<<n);j+=i)
			for (int k=0;k<i/2;k++)
				va[j+k]=min(va[j+k],va[j+k+i/2]);
	ans=2*c;
	for (int i=0;i<(1<<n);i++)
		ans=min(ans,va[i]+vb[((1<<n)-1)^i]);
	while (ans)
	{
		t[++cnt]=ans%10+'0';
		ans/=10;
	}
	if (!cnt)
		printf("0");
	while (cnt)
		printf("%c",t[cnt--]);
	printf("\n");
	return 0;
}