[开发工具]2021牛客多校8

比赛结果：

比赛过程：我开场先签了E，然后wmd和cqf开K，然后是我过了A，后面发现K枚举的数值不需要太大，改完直接过了。之后我和开D，cqf和wmd一起开cdq分治的F，我们先后过了D和E。最后一个小时我和cqf一在写J，但是直到结束也没有调整出来。

TE Rise of Shadows

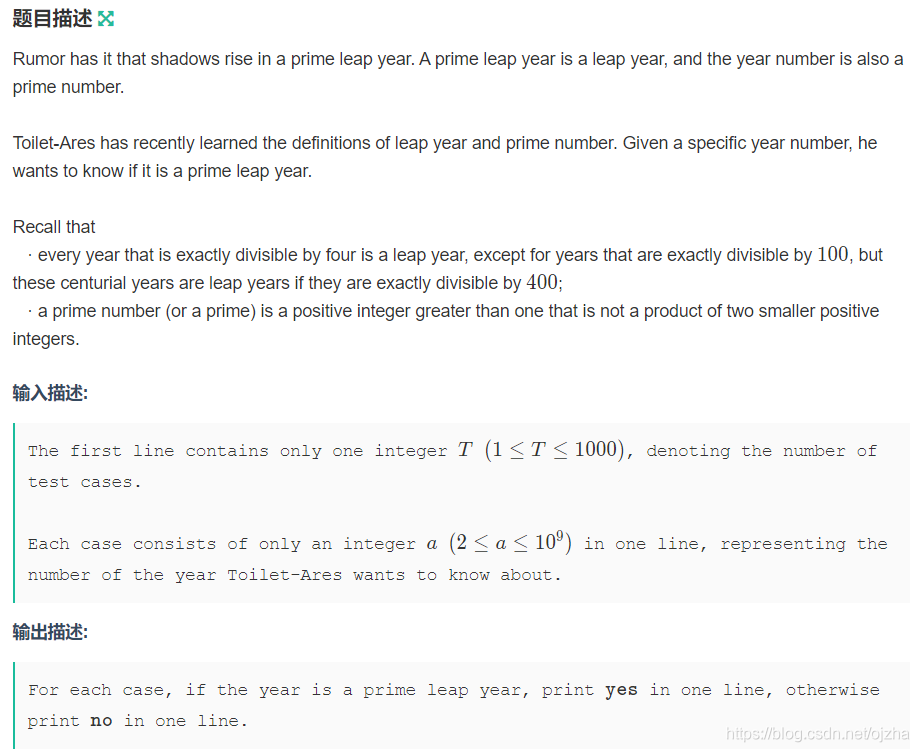
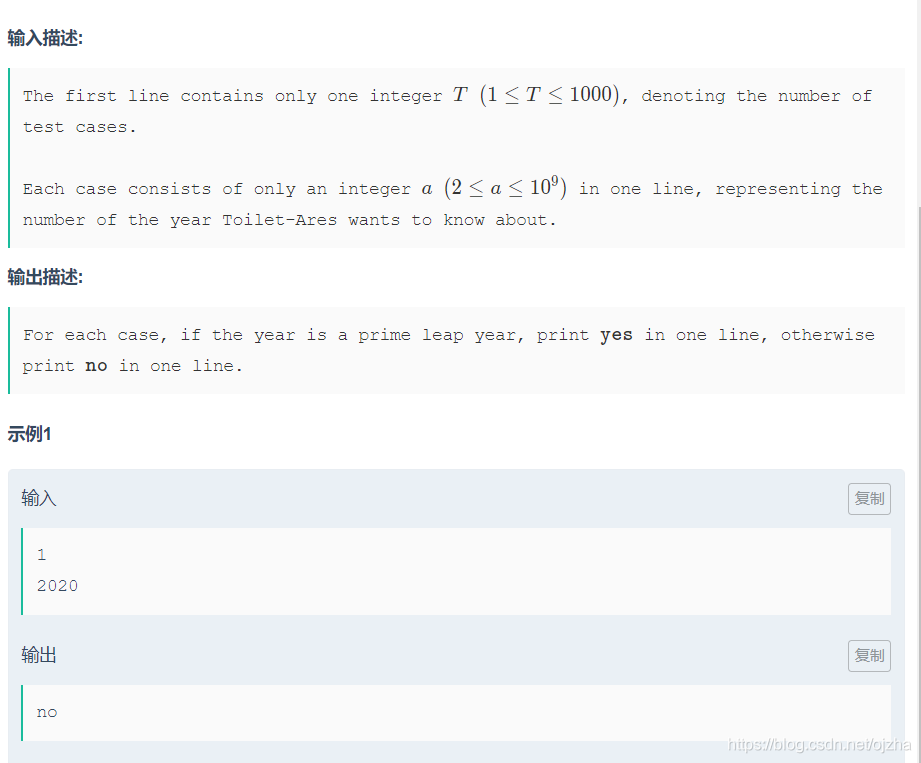
题意：给一个年份，判定是否是闰年并且这个年份是质数

idea：当然是不可能存在这样的年份的啊！！！！！！！

但是我就是那个傻傻判断闰年和质数的蒟蒻

#include<bits/stdc++.h>
#define LL long long
using namespace std;


bool check(LL x)
{
	if( x==1 ) return false;
	for(LL i=2;i<=sqrt(x)+1;i++)
	{
		if( x%i==0 ) return false;
	}
	return true;
}
bool judge( LL x )
{
	if( x%4==0 && x%100!=0 )
	{
		return true;
	}
	if( x%400==0 ) return true;
	
	return false;
}

LL n;
void solve()
{
	scanf("%lld",&n);
	if( judge(n) && check(n) ) printf("yes\n");
	else printf("no\n");
	return ;
}

int main()
{
	int T;
	cin>>T;
	while( T-- )
	solve();
	return 0;
}

TA Ares, Toilet Ares

题意： 求
$$(a+\prod _{i=1}^k(1?p_i))\%M,M=4933$$

idea：因为$p_i=\frac{y}{z}$，所以求个对模数的逆元就好（这个模数真有意思哈哈哈 ）

#include<bits/stdc++.h>
#define LL long long
using namespace std;

LL x,y,M=4933;
void exgcd(LL a,LL b)
{
    if( !b )
    {
        x = 1;
        y = 0;
        return ;
    }
    exgcd( b,a%b );
    LL t = x;
    x = y;
    y = t - (a/b)*y;
    return ;
}

bool pd = false;
LL n,m,k,a,l,ans=1;

void solve()
{
	cin>>n>>m>>k>>a>>l;
	for(int i=1;i<=k;i++)
	{
		LL xi,yi,zi;
		scanf("%lld %lld %lld",&xi,&yi,&zi);
		if( xi==0 ) continue;
		if( yi==zi ) pd = true;
		exgcd( zi , M );
        x = (x%M+M)%M;
//        cout<<x<<endl;
        ans = ans * (zi-yi) % M;
        ans = ans * x % M;
	}
	if( pd ) ans = 0;
	ans = (ans + a) % M;
	cout<<ans;
}

int main()
{
	//freopen("in.txt","r",stdin);
	
	solve();
	return 0;
}

TD OR

$c[i]=a[i?1]+a[i]=a[i?1]|a[i]+a[i?1]\&a[i]$
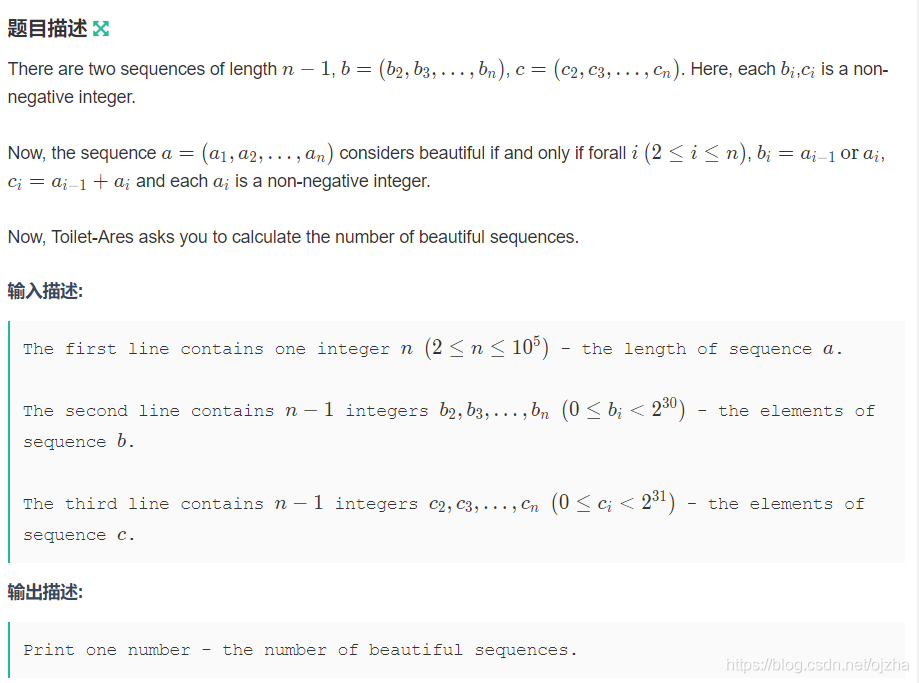
因此实际上是给出了相邻两位或、且的结果，询问有多少个ai序列满足要求
考虑每一位分开考虑。注意到，在这种情况下a1的取值能够确定整个序列，因此枚举a1的取值即可。

时间复杂度$O(n?log(a))$?

#include<bits/stdc++.h>
#define LL long long
#define N 101010
using namespace std;

LL n,b[N],c[N],ans = 1,tot = 0,a[N];

void solve()
{
	ans = 0;
	tot = 0;
	scanf("%lld",&n);
	for(int i=1;i<n;i++) scanf("%lld",&b[i]);
	for(int i=1;i<n;i++) scanf("%lld",&c[i]);
	for(int i=1;i<n;i++)
	{
		c[i] -= b[i];
		if( c[i]<0 )
		{
			printf("0\n");
			return ;
		}
	}
	for(LL i=0;i<=29;i++)
	{
		bool pd = false;
		memset(a,0,sizeof(a));
		LL nw = (1<<i);
		for(LL j=1;j<n;j++)
		{
			LL bi = b[j] & nw;
			LL ci = c[j] & nw;
			if( !bi && ci )
			{
				printf("0\n");
				return ;
			}
			if( bi==ci )
			{
				if( pd )
				{
					if( !bi && a[j] )
					{
						printf("0\n");
						return ;
					}
					if( bi && !a[j] )
					{
						printf("0\n");
						return ;
					}
				}
				pd = true;
				
				if( bi )
				{
					a[j] = a[j+1] = 1;
				}
				else 
				{
					a[j] = a[j+1] = 0;
				}
			}
			else if( pd )
			{
				a[ j+1 ] = a[j] ^ 1;
			}
		}
		if( !pd ) tot++;
	}
	ans = (1<<tot);
	printf("%lld\n",ans);
}


int main()
{
	//freopen("in.txt","r",stdin);
	solve();
	return 0;
}