Word2vec是一个学习单词向量的框架
IDEA:
- 我们有大量的文本 (corpus means ‘body’ in Latin. 复数为corpora)
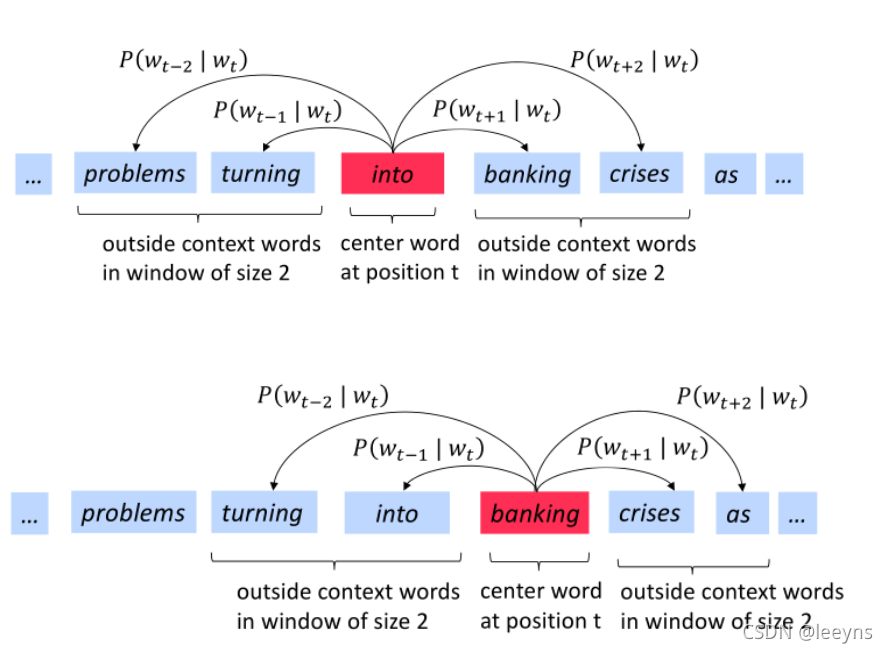
固定词汇表中的每个单词都由一个向量表示 - 文本中的每个位置 t,其中有一个中心词 c 和上下文(“外部”)单词 o
- 使用 c和 o的词向量的相似性来计算给定 c的 o的概率
- 不断调整词向量来最大化这个概率
目标函数
L
(
θ
)
=
∏
t
=
1
T
∏
?
m
≤
j
≤
m
j
≠
0
P
(
w
t
+
j
∣
w
t
;
θ
)
L(\theta)=\prod_{t=1}^{T} \prod_{-m \leq j \leq m \atop j \neq 0} P\left(w_{t+j} \mid w_{t} ; \theta\right)
L(θ)=t=1∏T?j?=0?m≤j≤m?∏?P(wt+j?∣wt?;θ)
损失函数
J
(
θ
)
=
?
1
T
log
?
L
(
θ
)
=
?
1
T
∑
t
=
1
T
∑
m
≤
j
≤
m
j
≠
0
log
?
P
(
w
t
+
j
∣
w
t
;
θ
)
J
(
θ
)
=
?
1
T
log
?
L
(
θ
)
=
?
1
T
∑
t
=
1
T
∑
m
≤
j
≤
m
j
≠
0
log
?
P
(
w
t
+
j
∣
w
t
;
θ
)
J(\theta)=-\frac{1}{T} \log L(\theta)=-\frac{1}{T} \sum_{t=1}^{T} \sum_{m \leq j \leq m \atop j \neq 0} \log P\left(w_{t+j} \mid w_{t} ; \theta\right)J(\theta)=-\frac{1}{T} \log L(\theta)=-\frac{1}{T} \sum_{t=1}^{T} \sum_{m \leq j \leq m \atop j \neq 0} \log P\left(w_{t+j} \mid w_{t} ; \theta\right)
J(θ)=?T1?logL(θ)=?T1?t=1∑T?j?=0m≤j≤m?∑?logP(wt+j?∣wt?;θ)J(θ)=?T1?logL(θ)=?T1?t=1∑T?j?=0m≤j≤m?∑?logP(wt+j?∣wt?;θ)
- L为目标函数,具体含义就是,遍历该语句,语句长度为T,意味着中心词的移动;
- 因为每次中心词时都要求该中心上下m个背景词和中心词的概率,所以背景词是t+j,j在-m到m之间,且不等于0;
- θ是超参数矩阵;
- 我们希望目标函数的值最大化,但是往往最大化不容易求解,而最小值更容易求解,所以将上述L转化为J,J为损失函数,也就是L的等价变化的负值。
Predict Function
P
(
w
t
+
j
∣
w
t
;
θ
)
P\left(w_{t+j} \mid w_{t} ; \theta\right)
P(wt+j?∣wt?;θ)如何计算?
每个单词都由两个向量表示:
- v w v_{w} vw? 当 w 是中心词时
- u w u_{w} uw? 当 w 是上下文词时
P ( o ∣ c ) = exp ? ( u o T v c ) ∑ w ∈ V exp ? ( u w T v c ) P(o \mid c)=\frac{\exp \left(u_{o}^{T} v_{c}\right)}{\sum_{w \in V} \exp \left(u_{w}^{T} v_{c}\right)} P(o∣c)=∑w∈V?exp(uwT?vc?)exp(uoT?vc?)?
使用梯度下降来更新参数
?
?
v
c
log
?
P
(
o
∣
c
)
=
?
?
v
c
log
?
exp
?
(
u
o
T
v
c
)
∑
w
∈
V
exp
?
(
u
w
T
v
c
)
=
?
?
v
c
(
log
?
exp
?
(
u
o
T
v
c
)
?
log
?
∑
w
∈
V
exp
?
(
u
w
T
v
c
)
)
=
?
?
v
c
(
u
o
T
v
c
?
log
?
∑
w
∈
V
exp
?
(
u
w
T
v
c
)
)
=
u
o
?
∑
w
∈
V
exp
?
(
u
w
T
v
c
)
u
w
∑
w
∈
V
exp
?
(
u
w
T
v
c
)
=
u
0
?
∑
x
∈
V
p
(
x
∣
x
)
u
x
\begin{aligned} \frac{\partial}{\partial v_{c}} \log P(o \mid c) &=\frac{\partial}{\partial v_{c}} \log \frac{\exp \left(u_{o}^{T} v_{c}\right)}{\sum_{w \in V} \exp \left(u_{w}^{T} v_{c}\right)} \\ &=\frac{\partial}{\partial v_{c}}\left(\log \exp \left(u_{o}^{T} v_{c}\right)-\log \sum_{w \in V} \exp \left(u_{w}^{T} v_{c}\right)\right) \\ &=\frac{\partial}{\partial v_{c}}\left(u_{o}^{T} v_{c}-\log \sum_{w \in V} \exp \left(u_{w}^{T} v_{c}\right)\right) \\ &=u_{o}-\frac{\sum_{w \in V} \exp \left(u_{w}^{T} v_{c}\right) u_{w}}{\sum_{w \in V} \exp \left(u_{w}^{T} v_{c}\right)}\\&=u_{0}-{\sum_{x\in V}p(x \mid x)u_{x}} \end{aligned}
?vc???logP(o∣c)?=?vc???log∑w∈V?exp(uwT?vc?)exp(uoT?vc?)?=?vc???(logexp(uoT?vc?)?logw∈V∑?exp(uwT?vc?))=?vc???(uoT?vc??logw∈V∑?exp(uwT?vc?))=uo??∑w∈V?exp(uwT?vc?)∑w∈V?exp(uwT?vc?)uw??=u0??x∈V∑?p(x∣x)ux??