[开发工具]论文《Graph Neural Networks for Social Recommendation》阅读

论文概况

本文是香港城市大学联合京东发表在WWW 2019上的一篇论文，CCF A会议，提出了模型GraphRec。这篇文章聚焦于社会化推荐（Social Recommendation），是社会化推荐较早的作品之一。

Introduction

论文解决三个问题：

1. user-item的显式交互包含不同分数（文中称之为意见，opinion），不同的分数代表不同的喜好，如何处理？
2. user和user之间的社交关系也有亲疏远近之分，不应该有连边就进行平均处理，如何体现？
3. user同时包含在use-item的交互和user-user的社交关系中，如何处理？

针对这三个问题，作者进行了GraphRec模型的设计。

GraphRec模型介绍

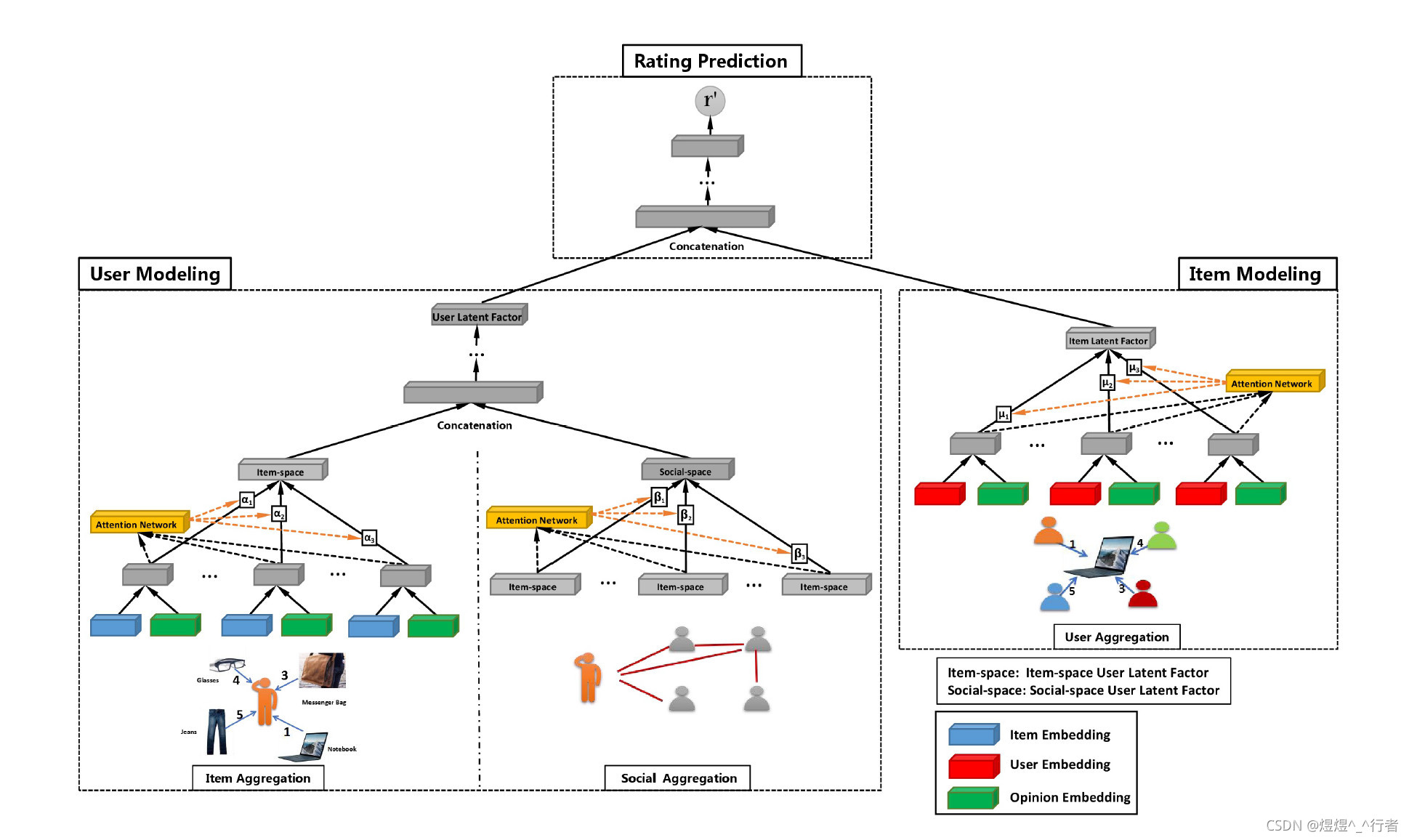
GraphRec可以分为两部分，User Modeling和Item Modeling，其中User Modeling又分为Item Aggregation和Social Aggregation，下面分别介绍。

User Modeling

Item Aggregation

Item Aggregation 这里是指通过user-item的交互矩阵进行用户在item-space的分解。

具体的，如下式所示，这里我们使用相对容易理解的符号进行重新书写，对文中一些不太友好的符号表示也进行了重新表示：

h i I = σ ( W ? A g g i t e m s ( { x i a ∣ ? a ∈ C i } ) + b ) σ ( W ? { ∑ a ∈ C ( i ) α i a x i a } + b ) h_i^I = \sigma (W \cdot Agg_{items}(\{x_{ia} | \forall a \in C_i \}) +b) \\ \sigma(W\cdot\{\sum_{a\in C(i)}\alpha_{ia} x_{ia}\} + b) hiI?=σ(W?Aggitems?({xia?∣?a∈Ci?})+b)σ(W?{a∈C(i)∑?αia?xia?}+b)

这里，$h_i^I$就表示item空间用户$i$的embedding表示，$Ag{g}_{items}(?)$表示item-space的聚合函数，可以看到使用加权求和并线性变换的方式进行表示，其中，${\alpha }_{ia}$表示权重，$x_{ia}$表示用户$i$和与其邻接的物品$a$的聚合向量，$C_i$表示用户$i$在item-space中与其邻接的所有物品集合。见下式：

$$x_{ia}=g_v([q_a||e_r])$$
$x_{ia}$使用物品$a$和评分等级$r$的可训练向量进行表示，$g_v(?)$表示融合函数，文中这里没有交代清楚，联系后文，应该是一个三层的MLP网络。

注意力系数${\alpha }_{ia}$如下面两式所示

$${\alpha }_{ia}^{?}=w_2^T?\sigma (W_1?[x_{ia}||p_i]+b_{1}1)+b_2$$

$${\alpha }_{ia}=\frac{\exp ({\alpha }_{ia}^{?})}{{\sum }_{c\in C_i}{\alpha }_{ic}^{?}}$$

可以看到，用户$i$和与其邻接的物品$a$的之间的注意力系数通过双层MLP进行计算，输入包括$x_{ia}$和$p_i$，因此可以理解为用户$i$和与其邻接的物品$a$之间的亲和力（affinity）指数。

Social Aggregation

后面的部分可以参考前面，我们不进行太详细的介绍，大致方式相同。

h i S = σ ( W ? A g g n e i g h b o r s ( { h o I ∣ ? o ∈ N i } ) + b ) σ ( W ? { ∑ o ∈ N ( i ) β i o h o I } + b ) h_i^S = \sigma (W \cdot Agg_{neighbors}(\{h_{o}^{I} | \forall o \in N_i \}) +b) \\ \sigma(W\cdot\{\sum_{o\in N(i)}\beta_{io} h_{o}^I\} + b) hiS?=σ(W?Aggneighbors?({hoI?∣?o∈Ni?})+b)σ(W?{o∈N(i)∑?βio?hoI?}+b)

类似的，$h_i^S$就表示social空间用户$i$的embedding表示，$Ag{g}_{neighbors}(?)$表示social-space的聚合函数，可以看到使用加权求和并线性变换的方式进行表示，其中，${\beta }_{io}$表示权重，$h_o^I$是item-space完成的用户$o$的item-space向量表示，$N_i$表示用户$i$在social-space中与其邻接的所有用户集合。具体的计算方式和Item Aggregation一样，篇幅原因，不一而足。

$h_i$表示最终的用户$i$的向量表示，先通过连接$h_i^S$与$h_i^I$，再通过多层感知机进行变换得到。

需要指出的是，这里的权重矩阵和向量如$W$、$b$等应该是不同的，在计算过程中应该进行区分，上面为了方便理解，没有进行更多的区分。

Item Modeling

直接在用户-物品的交互矩阵中进行提取，使用$z_j$进行表示，$Ag{g}_{users}$是其聚合函数，${\mu }_{jt}$表示注意力系数。

Rating Prediction和Model Training

使用MLP，先通过$h_i$和$z_j$的concatenation，然后通过多层感知机进行非线性变换得到最终的预测结果。

损失函数使用均方误差MSE进行表示，针对训练过程，一个三元组$(i,j,r)$表示用户$i$对物品$j$进行评分，评分为$r$，其中用户向量$h_i$、物品向量$z_j$、评分向量$e_r$都是随机初始化的可训练参数，除此以外各种MLP中的$W$和$b$也是可训练参数，共同构成训练参数。

总结一下

针对开头提出的三个问题，现总结如下：

1. 不同分数代表用户的不同意见，作者使用意见向量$e_r$进行表示，从而可以针对不同评分计算不同的意见注意力分数。
2. user和user之间，通过social aggregation时使用不同user之间的注意力分数${\beta }_{io}$进行计算
3. user两方面的属性，分别通过social space和item space进行计算，具体的，先通过item space的评分矩阵得到每个用户的item space表示$h_o^I$，将上面的item space表示$h_o^I$放进social space，完成用户之间的属性传播。

一点不成熟的评价

本文从社交网络和推荐交互图两部分进行学习，完成社会化推荐任务，值得一读。但是本人认为有以下几点需要注意一下：

1. 文章中的数学符号比较乱，容易混淆
2. 论文最后的related work含金量不高，基本没有GNN based social recommendation的相关论文，列举的方法都是比较久远的矩阵分解一类的方法，可以略过。
3. 公式中一些不规范表达需要注意一下